La logique du langage probabiliste
La logique du langage probabiliste
Résumé
Le texte traite de la logique du langage probabiliste appliquée au domaine médical, mettant en évidence comment l'incertitude est une partie intrinsèque de la pratique scientifique. À travers des concepts probabilistes et statistiques, on cherche à gérer et comprendre les incertitudes liées à la théorie et à la pratique médicale.
Le rôle de la probabilité dans la relation entre théorie et observation est souligné, en distinguant entre incertitude subjective et aléatoire. L'incertitude subjective concerne l'état de connaissance et de conviction des individus, tandis que l'aléatoire se réfère à l'absence de connexion certaine entre cause et effet.
Dans l'approche médicale, l'importance de comprendre et de distinguer entre probabilité subjective et objective est discutée. La probabilité subjective reflète la conviction individuelle, tandis que la probabilité objective est basée sur des données et des preuves empiriques.
Ensuite, le concept d'analyse probabiliste causale est approfondi, cherchant à quantifier la relation entre événements et processus aléatoires dans le diagnostic clinique. Une exposition détaillée est présentée sur la manière d'interpréter les probabilités conditionnelles et d'utiliser la partition de la pertinence causale pour formuler un diagnostic différentiel.
Enfin, le thème de l'interdisciplinarité dans la recherche scientifique est abordé, mettant en évidence l'importance d'une approche interdisciplinaire pour résoudre des problèmes complexes. On mentionne également la logique floue comme un outil possible pour gérer l'incertitude dans les contextes médicaux.
Logique de langage probabiliste en médecine
Chaque idée scientifique (que ce soit en médecine, en architecture, en ingénierie, en chimie ou dans tout autre domaine), lorsqu'elle est mise en pratique, est sujette à de petites erreurs et incertitudes. Les mathématiques - à travers la théorie des probabilités et l'inférence statistique - aident à contrôler avec précision et donc à contenir ces incertitudes. Il faut toujours considérer que dans tous les cas pratiques "les résultats dépendent également de nombreux autres facteurs extérieurs à la théorie", qu'il s'agisse des conditions initiales et environnementales, des erreurs expérimentales ou d'autre chose.
Toutes les incertitudes sur ces facteurs font de la relation théorie-observation une relation probabiliste. Dans l'approche médicale, il existe deux types d'incertitude qui pèsent le plus sur les diagnostics : l'incertitude subjective et le hasard.[1][2]Il devient donc essentiel dans ce scénario de distinguer ces deux incertitudes et de montrer que le concept de probabilité a des significations différentes dans ces deux contextes. Nous tenterons d'exposer ces concepts en reliant chaque étape cruciale à l'approche clinique qui a été rapportée dans les chapitres précédents et en particulier l'approche dans le contexte dentaire et neurologique en luttant pour la primauté du diagnostic pour notre chère Mary Poppins.
Incertitude subjective et hasard
Imaginons demander à Mary Poppins lequel des deux collègues médecins – le dentiste ou le neurologue – a raison. La question créerait une sorte d'agitation basée sur l'incertitude intérieure ; par conséquent, les notions de certitude et d'incertitude se réfèrent à des états épistémiques subjectifs des êtres humains et non à des états du monde extérieur, car il n'y a ni certitude ni incertitude dans ce monde. En ce sens, comme nous l'avons mentionné, il existe un monde intérieur et un monde extérieur à nous-mêmes qui ne répondent pas tous deux aux canons de l'incertitude, mais de la probabilité. Mary Poppins peut être subjectivement certaine ou incertaine quant à savoir si elle souffre de TMD ou d'une forme neuropathique ou neuromusculaire d'OP : ceci parce que « l'incertitude » est un état épistémique subjectif en dessous du seuil de connaissance et de croyance ; d'où le terme.
Incertitude subjective
Sans aucun doute, le terme « subjectif » effraie beaucoup, en particulier ceux qui ont l'intention de pratiquer la science en poursuivant l'idéal sain de « l'objectivité », tel que ce terme est perçu par le sens commun. Il convient donc d'apporter quelques précisions sur l'utilisation de ce terme dans ce contexte :
- « Subjectif » indique que l'évaluation de la probabilité dépend du statut d'information de l'individu qui l'effectue.
- « Subjectif » ne signifie pas arbitraire.
La soi-disant «objectivité», telle que perçue par ceux qui ne font pas partie de la recherche scientifique, est définie lorsqu'une communauté d'êtres rationnels partage le même état d'information. Mais même dans ce cas, on devrait plutôt parler d'« intersubjectivité » (c'est-à-dire le partage, par un groupe, d'opinions subjectives).
Dans les cas cliniques, précisément parce que les patients possèdent rarement des notions avancées de la médecine, l'incertitude subjective doit être prise en compte. Vivre avec l'incertitude nous oblige à utiliser une approche probabiliste.
Accidentée
Le hasard indique l'absence d'un certain lien entre la cause et l'effet. L'incertitude d'une union étroite entre la source et le phénomène est l'un des problèmes les plus néfastes dans la détermination d'un diagnostic. Dans un cas clinique un phénomène Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A(x)} (comme par exemple une malocclusion, une occlusion croisée, une béance, etc...) est aléatoirement associé à un autre phénomène Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B(x)} (comme une dégénérescence osseuse des ATM) ; lorsqu'il y a des exceptions pour lesquelles la proposition logique Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A(x) \rightarrow B(x)} ce n'est pas toujours vraie (mais c'est la plupart du temps), on dira que la relation Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A(x) \rightarrow B(x)} n'est pas toujours vraie mais elle est probable.
Probabilité subjective et objective
Dans ce chapitre, quelques sujets déjà traités dans le livre fantastique de Kazem Sadegh-Zadeh[3], qui aborde le problème de la logique du langage médical, sont repris et nous remodelons leur contenu en les renvoyant à notre cas clinique de Mary Poppins, pour garder notre compréhension plus proche des contextes dentaires. Les événements aléatoires et subjectivement incertains sont dits probables ; par conséquent, le hasard et l'incertitude sont traités comme des probabilités qualitatives, comparatives ou quantitatives. Pour clarifier ce concept, reprenons l'exemple de Mary Poppins. Un médecin, ayant entendu ses symptômes pourra dire que :
- Mary Poppins souffre probablement de TMD (terme qualitatif)
- Mary Poppins est plus susceptible d'avoir des TMD que des OP neuropathiques (terme comparatif : nombre de cas diagnostiqués de TMD versus nOP.
- La probabilité que Mary Poppins ait des TMD est de 0,15 (terme quantitatif, relatif à la population).
Probabilité subjective
Dans un contexte d'incertitude subjective humaine, les données probabilistes, qualitatives, comparatives et/ou quantitatives peuvent être interprétées comme une mesure d'incertitude subjective par le clinicien, afin de rendre numériquement représentables les « états de conviction ». Par exemple, dire que "la probabilité que Mary Poppins soit affectée par les TMD est de 0,15 des cas" revient à dire "dans la mesure de 15%, je crois que Mary Poppins est affectée par les TMD" ; ce qui signifie que le degré de conviction est le degré de probabilité subjectivey.
Probabilité objective
D'autre part, les événements et les processus aléatoires ne peuvent pas être décrits par des processus déterministes sous la forme « si A alors B ». Les statistiques sont utilisées pour quantifier la fréquence d'association entre A et B et pour représenter les relations entre eux comme un degré de probabilité qui introduit le degré de probabilité objective. Dans le sillage de la probabilisation croissante de l'incertitude et de l'aléatoire en médecine depuis le XVIIIe siècle, le terme « probabilité » est devenu un élément respecté du langage médical, de la méthodologie et de l'épistémologie. Malheureusement, les deux types de probabilité, la probabilité subjective et la probabilité objective, ne sont pas différenciés avec précision en médecine, et la même chose se produit également dans d'autres disciplines. Le fait fondamental demeure que le sens le plus important que la théorie des probabilités a généré en médecine, en particulier dans les concepts de probabilité en étiologie, épidémiologie, diagnostic et thérapie, est sa contribution à notre compréhension et à notre représentation de l'accident biologique.
Analyse probabiliste-causale
De ces prémisses, il est clair que le diagnostic clinique est effectué en utilisant la méthode dite hypothético-déductive appelée DN[4] (deductive-nomological model[5]). Mais ce n'est pas réaliste, car les connaissances médicales utilisées dans la prise de décision clinique ne contiennent guère de lois déterministes causales pour permettre des explications causales et, par conséquent, pour formuler des diagnostics cliniques, entre autres dans le contexte spécialisé. Essayons d'analyser à nouveau le cas de notre Mary Poppins, en essayant cette fois une approche probabiliste-causale. Considérons un nombre d'individus, y compris les personnes qui signalent une douleur orofaciale qui ont généralement une dégénérescence osseuse de l'articulation temporo-mandibulaire. Cependant, il peut également y avoir d'autres causes apparemment sans rapport. Nous devons traduire mathématiquement la « pertinence » que ces incertitudes causales ont dans la détermination d'un diagnostic.
La pertinence décontractée
Pour ce faire on considère le degré de pertinence causale Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (cr)} d'un événement Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_1} par rapport à un événement Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_2} où :
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_1} = patients atteints de dégénérescence osseuse de l'articulation temporo-mandibulaire
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_2} = patients signalant des douleurs bucco-faciales
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_3} =patients sans dégénérescence osseuse de l'articulation temporo-mandibulaire
Nous utiliserons la probabilité conditionnelle Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(A \mid B)} , c'est-à-dire la probabilité que l'événement Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} ne se produise qu'après que l'événement Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B} se soit déjà produit. Avec ces prémisses, la pertinence causale Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle cr} de l'échantillon Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} de patients est :
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle cr=P(E_2 \mid E_1)- P(E_2 \mid E_3)}
où
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(E_2 \mid E_1)} indique la probabilité que certaines personnes (parmi Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} prises en compte) souffrent de Douleurs Orofaciales causées par la dégénérescence osseuse de l'articulation temporo-mandibulaire,
- alors que
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(E_2 \mid E_3)} indique la probabilité que d'autres personnes (toujours parmi Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} pris en considération) souffrent de Douleur Orofaciale conditionnée par autre chose qu'une dégénérescence osseuse de l'articulation temporo-mandibulaire.
- Étant donné que toutes les probabilités suggèrent que Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(A \mid B)} est une valeur comprise entre Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0 } et Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1 } , le paramètre Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (cr)} sera un nombre compris entre Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -1 } et Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1 } .
- Les significations que nous pouvons donner à ce nombre sont les suivantes:
- on a les cas extrêmes (qui en réalité ne se produisent jamais) qui sont :
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle cr=1} indiquant que la seule cause de douleur orofaciale est la dégénérescence osseuse de l'ATM,
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle cr=-1} ce qui indique que la cause de la douleur orofaciale n'est jamais une dégénérescence osseuse de l'ATM mais autre chose,
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle cr=0} indiquant que la probabilité que la douleur orofaciale soit causée par une dégénérescence osseuse de l'ATM ou autrement est exactement la même,
- et les cas intermédiaires (qui sont les cas réalistes)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle cr>0} indiquant que la cause de la douleur orofaciale est plus susceptible d'être une dégénérescence osseuse de l'ATM,
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle cr<0} ce qui indique que la cause de la douleur orofaciale n'est probablement pas la dégénérescence osseuse de l'ATM.
Deuxième approche clinique
(survolez les images)
Soit alors Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(D)} la probabilité de trouver, dans l'échantillon de nos Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} personnes, des individus qui présentent les éléments appartenant à l'ensemble Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D=\{\delta_1,\delta_2,...,\delta_n\}} précité.
Afin de tirer parti des informations fournies par ce jeu de données, le concept de partition de pertinence causale est introduit:
La partition de la pertinence causale
- Soit toujours Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} le nombre de personnes sur lesquelles nous devons mener les analyses, si nous divisons (sur la base de certaines conditions comme expliqué ci-dessous) ce groupe en Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} sous-ensembles Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_i} avec Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i=1,2,\dots,k} , un cluster est créé qui s'appelle un "ensemble de partition" Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi} :
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi = \{C_1, C_2,\dots,C_k \} \qquad \qquad \text{avec} \qquad \qquad C_i \subset n , }
où avec le symbolisme Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_i \subset n } il indique que la sous-classe Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_i} est contenue dans Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} .
La partition Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi} , pour être définie comme une partition de pertinence causale, doit avoir ces propriétés :
- Pour chaque sous-classe Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_i} la condition doit appliquer Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle rc=P(D \mid C_i)- P(D )\neq 0, } c'est-à-dire la probabilité de trouver dans le sous-groupe Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_i} une personne qui présente les symptômes, les signes cliniques et les éléments appartenant à l'ensemble Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D=\{\delta_1,\delta_2,...,\delta_n\}} . Une partition causalement pertinente de ce type est dite homogène.
- Chaque sous-ensemble Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_i} doit être «élémentaire», c'est-à-dire qu'il ne doit pas être divisé en d'autres sous-ensembles, car s'ils existaient, ils n'auraient aucune pertinence causale.
Supposons maintenant, par exemple, que la population échantillon Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} , à laquelle appartient notre bonne patiente Mary Poppins, soit une catégorie de sujets âgés de 20 à 70 ans. Nous supposons également que dans cette population nous avons ceux qui présentent les éléments appartenant à la ensemble de données Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D=\{\delta_1,.....\delta_n\}} qui correspondent aux tests de laboratoire mentionnés ci-dessus et précis dans 'La logique du langage classique'. Supposons que dans un échantillon de 10 000 sujets de 20 à 70 nous aurons une incidence de 30 sujets Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p(D)=0.003} présentant des signes cliniques Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta_1} et Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta_4 } . Nous avons préféré utiliser ces rapports pour la démonstration du processus probabiliste car dans la littérature les données concernant les signes cliniques et les symptômes des troubles temporo-mandibulaires présentent une trop grande variation ainsi qu'une incidence trop élevée à notre avis.[6][7][8][9][10]
Un exemple de partition avec probabilité présumée dans laquelle la dégénérescence de l'ATM (Deg.TMJ) se produit en conjonction avec des troubles temporo-mandibulaires (TMD) serait le suivant :
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(D| Deg.TMJ \cap TMDs)=0.95 \qquad \qquad \; } | où | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \C_1 \equiv Deg.TMJ \cap TMDs} | |||
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(D| Deg.TMJ \cap noTMDs)=0.3 \qquad \qquad \quad } | où | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_2\equiv Deg.TMJ \cap noTMDs} | |||
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(D| no Deg.TMJ \cap TMDs)=0.199 \qquad \qquad \; } | où | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_3\equiv no Deg.TMJ \cap TMDs} | |||
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(D| noDeg.TMJ \cap noTMDs)=0.001 \qquad \qquad \;} | où |
Situations cliniques
Ces probabilités conditionnelles démontrent que chacune des quatre sous-classes de la partition est causalement pertinente pour les données patient Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D=\{\delta_1,.....\delta_n\}} dans l'échantillon de population Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle PO} . Compte tenu de la partition susmentionnée de la classe de référence, nous avons les situations cliniques suivantes :
- Mary Poppins Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \in} dégénérescence de l'articulation temporo-mandibulaire Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cap} Troubles temporo-mandibulaires
- Mary Poppins Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \in} dégénérescence de l'articulation temporo-mandibulaire Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cap} pas de troubles temporo-mandibulaires
- Mary Poppins Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \in} pas de dégénérescence de l'articulation temporo-mandibulaire Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cap} Troubles temporo-mandibulaires
- Mary Poppins Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \in} pas de dégénérescence de l'articulation temporo-mandibulaire Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cap} pas de troubles temporo-mandibulaires
Pour arriver au diagnostic final ci-dessus, nous avons effectué une analyse probabiliste-causale de l'état de santé de Mary Poppins dont les données initiales étaient de Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D=\{\delta_1,.....\delta_n\}} .
En général, on peut se référer à un processus logique dans lequel on examine les éléments suivants :
- un individu: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a}
- son jeu de données initialFailed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D=\{\delta_1,.....\delta_n\}}
- un échantillon de population Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} auquel il appartient,
- une probabilité de base
A ce stade, nous devons introduire des arguments trop spécialisés qui éloigneraient le lecteur du sujet mais qui ont une grande importance épistémique pour lesquels nous essaierons d'extraire le fil logique le plus décrit du concept Analysandum/Analysans.
L'analyse probabiliste-causale de Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D=\{\delta_1,.....\delta_n\}} est alors un couple des formes logiques suivantes (Analysandum / Analysans[11])
- Analysandum Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \{P(D),a\}} : est une forme logique qui contient deux paramètres : la probabilité Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(D)} de sélectionner une personne qui présente les symptômes et les éléments appartenant à l'ensemble Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D=\{\delta_1,\delta_2,...,\delta_n\}} , et l'individu générique Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} qui est sujet à ces symptômes.
- Analysan Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \{\pi,a,KB\}} :est une forme logique qui contient trois paramètres : la partition Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi} , l'individu générique Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} appartenant à l'échantillon de population Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} et Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle KB} (Base de connaissances) qui comprend un ensemble d'énoncés Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n>1} de probabilité conditionnée.
Par exemple, on peut conclure que le diagnostic définitif est le suivant :
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(D| Deg.TMJ \cap TMDs)=0.95} - cela signifie que notre Mary Poppins est touchée à 95% par les TMD, puisqu'elle a une dégénérescence de l'articulation temporo-mandibulaire en plus des données positives Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D=\{\delta_1,.....\delta_n\}}
Considérations finales
Nous avons parcouru un chemin long et tortueux pour mieux comprendre la complexité rencontrée par le confrère aux prises avec la très lourde responsabilité éthique de poser un diagnostic. Cependant, cette tâche devient encore plus complexe lorsque nous devons être détaillés et prudents dans l'établissement d'un diagnostic différentiel. Ici, nous entrons dans un sujet délicat, qui est lié au contenu épistémologique et qui a d'abord été rapporté dans l'"Introduction". On parle de:
- Interdisciplinarité :
En politique scientifique, il est généralement reconnu que la résolution de problèmes basée sur la science nécessite une recherche interdisciplinaire (IDR), comme le propose le projet européen Horizon 2020.[12] Dans une étude récente, les auteurs se concentrent sur la question de savoir pourquoi les chercheurs ont des difficultés cognitives et épistémiques à réalisation d'IDR. On pense que la perte d'intérêt philosophique pour l'épistémologie de la recherche interdisciplinaire est causée par un paradigme philosophique de la science appelé "Physics Paradigm of Science", qui empêche la reconnaissance des changements importants de l'IDR à la fois dans la philosophie de la science et de la recherche. Le paradigme philosophique alternatif proposé, appelé 'Engineering Paradigm of Science', fait des hypothèses philosophiques alternatives sur des aspects tels que le but de la science, le caractère de la connaissance, les critères épistémiques et pragmatiques pour l'acceptation de la connaissance et le rôle des outils technologiques. Par conséquent, les chercheurs scientifiques ont besoin d'échafaudages dits métacognitifs pour les aider dans l'analyse et la reconstruction de la façon dont la « connaissance » est construite dans différentes disciplines. Dans la recherche interdisciplinaire, les échafaudages métacognitifs aident la communication interdisciplinaire à analyser et à articuler la manière dont la discipline construit les connaissances.[13][14]
Ce concept est lié au sujet abordé précédemment dans lequel le collègue doit être conscient de sa propre 'Incertitude subjective' (due à un langage logique classique 'malade ou en bonne santé') et de 'l'Incertitude objective' (due à un langage logique probabiliste ' probablement malade ou probablement en bonne santé »). Il n'est pas compliqué de prouver cette assertion : l'incertitude dont nous parlons provient du fait que les éléments, assertions, données, classes et sous-classes cités et qui construisent l'appareil de la logique du langage probabiliste : Analysandum Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \{P(D),a\}}
et Analysan Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \{\pi,a,KB\}}
sont des éléments qui existent dans un monde spécifique, et en l'occurrence dans un contexte dentaire dans lequel l'élément Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle KB}
du processus indique indiscutablement une "connaissance de base" uniquement dans un contexte dentaire spécifique.
Cette conclusion confirmée par le dentiste était la suivante :
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(D| Deg.TMJ \cap TMDs)=0.95}
ou mieux : je crois à 95 % que Mary Poppins est affectée par les TMD puisqu'elle a une dégénérescence de l'articulation temporo-mandibulaire en plus de la positivité des données Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D=\{\delta_1,\dots\delta_n\}} . Mais quelque chose d'étrange se produit parce que de nulle part, un chercheur, qui utilise des "échafaudages métacognitifs"[15] pour une mise en œuvre dans l'analyse et la reconstruction de la façon dont les "connaissances" sont construites dans différentes disciplines, demande une réponse à la question suivante du dentiste
et augmentez la dose : soumettez Mary Poppins aux tests électrophysiologiques trigéminaux suivants, étiquetez-les comme nous l'avons fait précédemment pour l'ensemble de données Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D=\{\delta_1,\dots\delta_n\}}
en générant un autre ensemble contenant un nombre Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m}
de données inconnues (n'appartenant pas à la branche purement dentaire) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C=\{\gamma_1,\dots\gamma_m\}}
créant ainsi un tout nouvel ensemble que nous appellerons Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{unknow}= D+C=\{\delta_1,\dots,\delta_n,\gamma_1,\dots,\gamma_m\}}
(Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{unknown}}
précisément dû à la présence de données inconnues du contexte dentaire).
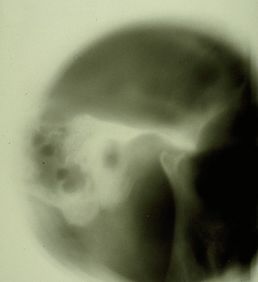
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta_1=} Rapport radiologique positif de l'ATM dans la figure 2
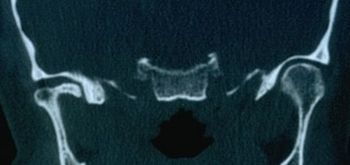
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta_2=} Rapport CT positif de l'ATM dans la figure 3
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta_3=} Rapport axiographique positif des tracés condyliens de la figure 4
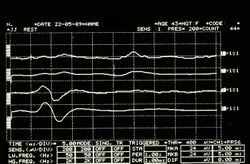
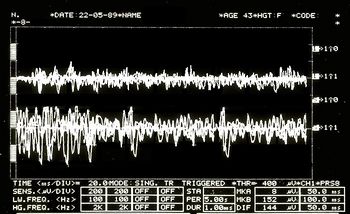
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta_4=} Modèle d'interférence EMG asymétrique dans la figure 5
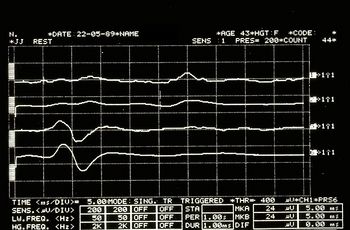
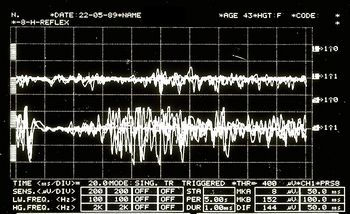
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\gamma _{1}}=} Secousse de la mâchoire dans la figure 6
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\displaystyle \gamma _{2}}=} Période de silence mécanique dans la figure 7
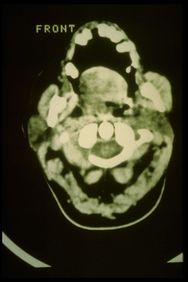
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\displaystyle \gamma _{3}}=} CT muscle masséter droit sur la figure 8
Troisième approche clinique
(survolez les images)
De cette manière, il a été démontré que, inévitablement,
En explorant cette ligne de périmètre du contexte spécialisé, nous créerons une zone proche de celle-ci que nous appellerons la « zone floue » ou « logique floue » dont nous parlerons dans le chapitre suivant.
«... de ce qu'il semble que même avec une logique de langage probabiliste nous pourrons définir un diagnostic exact.»
(en fait, pour cette raison, nous devrions également considérer le|Fuzzy Logic Language]] ) |
- ↑ Vázquez-Delgado E, Cascos-Romero J, Gay-Escoda C, «Myofascial pain associated to trigger points: a literature review. Part 2: differential diagnosis and treatment», in Med Oral Patol Oral Cir Bucal, 2007».
PMID:20173729
DOI:10.4317/medoral.15.e639 - ↑ Thoppay J, Desai B, «Oral burning: local and systemic connection for a patient-centric approach», in EPMA J, 2019».
PMID:30984309 - PMCID:PMC6459460
DOI:10.1007/s13167-018-0157-3 - ↑ Sadegh-Zadeh Kazem, «Handbook of Analytic Philosophy of Medicine», Springer, 2012, Dordrecht».
ISBN: 978-94-007-2259-0
DOI:10.1007/978-94-007-2260-6 . - ↑ Sarkar S, «Nagel on Reduction», in Stud Hist Philos Sci, 2015».
PMID:26386529
DOI:10.1016/j.shpsa.2015.05.006 - ↑ DN model of scientific explanation, also known as Hempel's model, Hempel–Oppenheim model, Popper–Hempel model, or covering law model
- ↑ Pantoja LLQ, De Toledo IP, Pupo YM, Porporatti AL, De Luca Canto G, Zwir LF, Guerra ENS, «Prevalence of degenerative joint disease of the temporomandibular joint: a systematic review», in Clin Oral Investig, 2019».
PMID:30311063
DOI:10.1007/s00784-018-2664-y - ↑ De Toledo IP, Stefani FM, Porporatti AL, Mezzomo LA, Peres MA, Flores-Mir C, De Luca Canto G, «Prevalence of otologic signs and symptoms in adult patients with temporomandibular disorders: a systematic review and meta-analysis», in Clin Oral Investig, 2017».
PMID:27511214
DOI:10.1007/s00784-016-1926-9 - ↑ Bonotto D, Penteado CA, Namba EL, Cunali PA, Rached RN, Azevedo-Alanis LR, «Prevalence of temporomandibular disorders in rugby players», in Gen Dent».
PMID:31355769 - ↑ da Silva CG, Pachêco-Pereira C, Porporatti AL, Savi MG, Peres MA, Flores-Mir C, De Luca Canto G, «Prevalence of clinical signs of intra-articular temporomandibular disorders in children and adolescents: A systematic review and meta-analysis», in Am Dent Assoc, 2016». - PMCID:26552334
DOI:10.1016/j.adaj.2015.07.017 - ↑ Gauer RL, Semidey MJ, «Diagnosis and treatment of temporomandibular disorders», in Am Fam Physician, 2015».
PMID:25822556 - ↑ Westmeyer H, «The diagnostic process as a statistical-causal analysis», in APA, 1975».
DOI:10.1007/BF00139821
This is an Open Access resource! - ↑ European Union, Horizon 2020
- ↑ Boon M, Van Baalen S, «Epistemology for interdisciplinary research - shifting philosophical paradigms of science», in Eur J Philos Sci, 2019».
DOI:10.1007/s13194-018-0242-4 9(1):16. - ↑ Boon M, «An engineering paradigm in the biomedical sciences: Knowledge as epistemic tool», in Prog Biophys Mol Biol, 2017».
DOI:10.1016/j.pbiomolbio.2017.04.001 - ↑ Boon M, Van Baalen S, «Epistemology for interdisciplinary research - shifting philosophical paradigms of science», in Eur J Philos Sci, 2019».
PMID:30873248 - PMCID:PMC6383598
DOI:10.1007/s13194-018-0242-4
This is an Open Access resource!
particularly focusing on the field of the neurophysiology of the masticatory system