Asse Cerniera verticale

Home

Scientific project

Social project

Our story

Scientific community

Book index

Our network

Frisardi Masticationpedia Network

Fontana Masticationpedia Network

Ed. Lab

Donate

Contact

Change language

German

Spanish

French

Italian

Asse Cerniera verticale

 

Article by  Gianni Frisardi

 

Introduzione

Nel capitolo precedente, 'Transverse Hinge Axis', abbiamo introdotto la cinematica mandibolare concentrandoci sul piano sagittale. Abbiamo osservato come, durante i movimenti di protrusione e retrusione, la mandibola non si muova semplicemente lungo l'asse $X$, ma esegua anche una rotazione attorno al centro di rotazione dell'asse $Y$. Questo movimento condilare si riflette a livello anteriore, dove l'incisivo mandibolare si sposta con traiettorie curvilinee inverse, risultato di un moto spaziale complesso determinato dalla rototraslazione sugli assi condilari. Lo spazio angolare risultante è di fondamentale importanza per permettere alla mandibola di ruotare liberamente senza ostacoli con escursioni fluide durante il movimento masticatorio. Questo fenomeno è anche conosciuto come 'Spazio libero Interincisivo'.

Questo 'Spazio libero Interincisivo' è cruciale per le funzioni masticatorie. Tuttavia, strumenti come il Sirognatograph e i sistemi elettromagnetici tradizionali tendono a ignorare la componente rotazionale associata ai movimenti condilari, concentrandosi principalmente sulle traslazioni. Sebbene sembri sufficiente per la registrazione del movimento, tale approccio risulta incompleto, data la complessità dei movimenti mandibolari a sei gradi di libertà.

Cinematica Mandibolare a Sei Gradi di Libertà

Il movimento mandibolare avviene in uno spazio tridimensionale e può essere descritto da un complesso moto spaziale. Ogni condilo è associato a tre assi principali:

L'asse $Y$ (latero-mediale), attorno al quale ruota la mandibola, creando l'asse cerniera trasversale ($_{t}HA$ transverse Hinge Axis).

L'asse $Z$ (verticale), con il proprio centro di rotazione sull'asse cerniera verticale ($_{v}HA$)

L'asse $X$ (antero-posteriore), che determina la rotazione attorno all'asse cerniera orizzontale ($_{o}HA$)

In riferimento agli assi appena definiti, andiamo a introdurre tre piani di riferimento:

Nel contesto del movimento spaziale del condilo, è fondamentale comprendere la relazione tra gli assi di rotazione e i piani di riferimento anatomici.

• Piano sagittale: In questo piano possiamo visualizzare il tracciato condilare risultante dal movimento di rototraslazione dell'asse trasversale ($_{t}HA$).
• Piano coronale: Associato all'asse orizzontale ($_{o}HA$).
• Piano assiale: Riferito al movimento generato attorno all'asse verticale ($_{v}HA$, noto anche come asse cerniera verticale).

Va sottolineato che un piano non è generato da un asse: un asse, al più, può essere contenuto in un piano o rappresentare una direzione lungo la quale si possono descrivere movimenti o proiezioni. Più precisamente, l’inviluppo di un asse in movimento genera una 'superficie rigata', che descrive le traiettorie spaziali associate.

Asse cerniera verticale

Ci concentreremo sull’asse cerniera verticale ($_{v}HA$) per la sua rilevanza nei sistemi di replicazione elegnatografici, pantografica ed assiografica. Tuttavia, prima di procedere, è necessario esaminare il razionale su cui si basa la Gnatologia Classica, per comprendere come i piani e gli assi interagiscono nel descrivere i movimenti condilari.

• Il pantografo analogico è stato considerato come un dispositivo che riproduceva accuratamente i movimenti di confine dei tracciati condilari del paziente e li trasferiva su un articolatore completamente regolabile tramite le sue 6 piastrine. Successivamente, si è riportato che anche il pantografo elettronico registrava i determinanti condilari con un intervallo accettabile. ( argomento che affronteremo dettagliatamente nei prossimi capitoli)
• Gli investigatori hanno sottolineato l’influenza della corretta registrazione dei movimenti mandibolari sulla morfologia occlusale risultante dei denti posteriori, espressa negli angoli delle cuspidi e nella direzione dei solchi come effetto diretto della variazione dei determinanti condilari.
• Un determinante particolare del movimento condilare, la traslazione laterale immediata mandibolare (Movimento di Bennett) dei condili, è stato oggetto di notevole dibattito e confusione nella letteratura protesica. Tuttavia, una recente revisione sistematica della letteratura ha riportato una mancanza di prove riguardo al significato clinico o alle implicazioni di questo movimento. ( argomento che approceremo in modo più dettagliato in questo capitolo).

Come si può notare il tema si basa sostanzialmente sulla meccanica razionale, argomento non banale, in cui si integrano concetti di geometria, matematica e meccanica ed è auspicabile, quindi, capire il profondo senso concettuale del processo di replicazione dei movimenti mandibolare, per evidenziarne l'eventuale anomalia. Per fare ciò si è inizializzato il percorso analitico prendendo i lavori prestigiosi eseguiti da Lund e Gibbs riguardo la cinematica mandibolare con lo strumento datato ma ancora attuale chiamato, appunto, 'Replicator'.

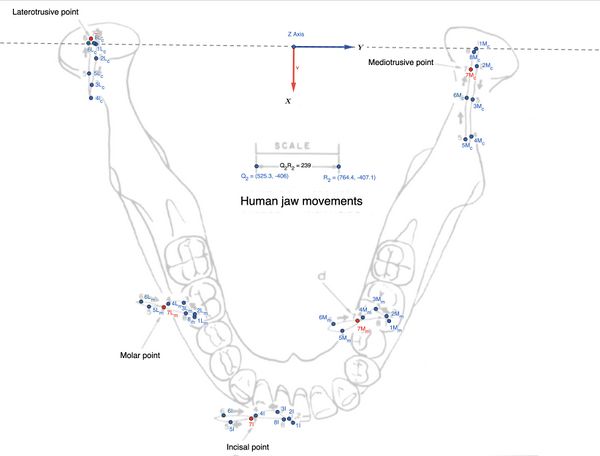
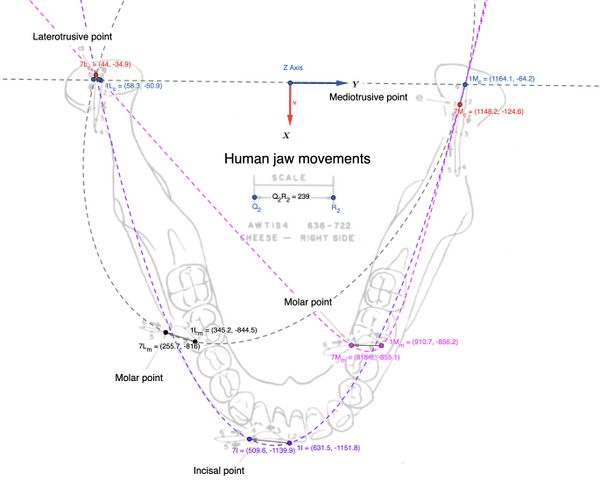
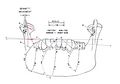
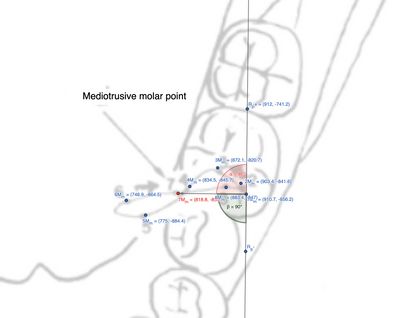
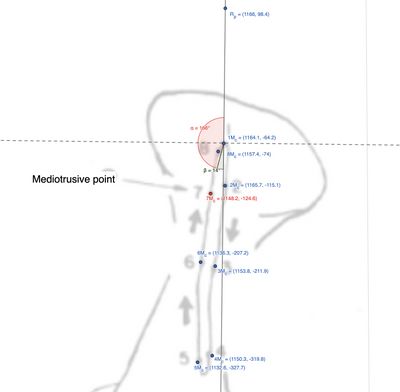
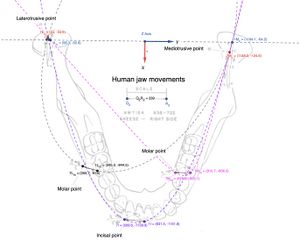
In questo capitolo, si è focalizzata l'attenzione della cinematica mandibolare sul piano assiale e cioè generata dalla cinematica dell'asse verticale $_{v}HA$ e descriveremo ,perciò, il fenomeno interpretando un tracciato estratto dal lavoro di Lund e Gibs, Figura 1 in cui viene rappresentata la cinematica mandibolare marcati ogni 20 msec. ( vedi figura e popup Questa figura mostra la rappresentazione dei movimenti masticatori umani con un focus sulla cinematica mandibolare, evidenziando i Punti condilariQuesti punti rappresentano i condili laterotrusivi e mediotrusivi. Il Laterotrusive point (a sinistra) e il Mediotrusive point (a destra) tracciano la posizione dei condili della mandibola durante un movimento masticatorio laterale, che include movimenti complessi di traslazione e rotazione. I punti numerati (1L, 2L, 3L, ecc.) seguono il movimento del condilo laterotrusivo nel tempo, mentre i punti 1M, 2M, ecc. seguono il condilo mediotrusivo e i tracciati dei movimenti su i punti occlusali Punto molareIl Molar point (situato in basso a sinistra) rappresenta il percorso tracciato dal molare durante il movimento masticatorio. Come per i condili, anche qui i punti numerati rappresentano le varie posizioni del molare nel tempo e del Punto incisaleL'Incisal point (in basso a destra) rappresenta il percorso dell'incisivo durante la masticazione. I punti numerati (1, 2, 3, ecc.) descrivono la traiettoria dell'incisivo nel tempo. La figura include un sistema di riferimento tridimensionale con assi cartesiani X, Y, e Z. L'asse Z è orientato verticalmente, l'asse Y rappresenta il movimento laterale (sinistra/destra) della mandibola, e l'asse X indica il movimento antero-posteriore (avanti/indietro).Movimenti masticatori: I tracciati mostrano l'evoluzione dei movimenti durante il ciclo masticatorio, descrivendo la traslazione e rotazione di ciascuna porzione del sistema mandibolare (condili, molari e incisivi) nel tempo.)

Figura 1: Cinematica mandibolare sul piano assiale rappresentata dai markers prelevati dallo strumento ogni 20 mSec. Questi punti rappresentano i condili laterotrusivi dal punto $L_{c}$ e mediotrusivi $M_{c}$. Il Laterotrusive point (a sinistra) e il Mediotrusive point (a destra) tracciano la posizione dei condili della mandibola durante un movimento masticatorio laterale, che include movimenti complessi di traslazione e rotazione. I punti numerati ($1L_{c}$....$8L_{c}$) seguono il movimento del condilo laterotrusivo nel tempo, mentre i punti $1M_{c}$.... $8M_{c}$seguono il condilo mediotrusivo. Nell'area del 'Molar point', 'Incisal point' e del molare controlaterale 'Mediotrusive molar point' rappresenta il percorso occlusali durante la masticazione.

Nota sulla Precisione e Sugli Obiettivi dello Studio

Questo studio si propone di fornire una comprensione concettuale dei principi cinematici coinvolti nella dinamica masticatoria, con particolare riferimento alla biomeccanica mandibolare. Sebbene i calcoli presentati siano stati svolti con rigore e utilizzando metodologie matematiche consolidate, potrebbero emergere discrepanze dovute a:

Approssimazioni nei dati numerici: Lieve differenze nei valori cartesiani utilizzati, imputabili a variabili operative o a scelte dell'operatore nell'acquisizione dei dati.

Limiti di rappresentazione: L'utilizzo di numeri approssimati per motivi pratici, soprattutto in calcoli iterativi, potrebbe introdurre variazioni infinitesimali rispetto ai valori teoricamente perfetti.

Finalità del lavoro: Lo scopo principale è descrivere e comprendere il comportamento cinematico del sistema masticatorio, piuttosto che ottenere una precisione assoluta come richiesto in un contesto di ricerca ingegneristica avanzata o in una tesi di dottorato in ingegneria meccanica.

I risultati e le analisi presentate mirano quindi a illustrare concetti e fenomeni in modo chiaro e applicabile, piuttosto che a fornire un riferimento definitivo. L'interpretazione deve essere orientata verso l'obiettivo clinico e didattico del lavoro, senza pretesa di impeccabilità formale sul piano matematico o ingegneristico.

Iniziamo, perciò, con la descrizione dell'analisi cinematica passando per alcuni cruciali step: la rappresentazione dell'immagine su Geogebra, la calibrazione attraverso scalatura delle distanze e la conversione da pixel a millimetri.

, attraverso l'uso dell'immagine riportata, il complesso processo cinematico condilare e dei punti occlusali e per prima cosa bobbiamo necessariamente calibrare la figura e convertirla in pixel.

Descrizione della Calibrazione: da Pixel a Millimetri

La calibrazione di un'immagine per ottenere misurazioni accurate richiede l'attenzione a diversi fattori critici. Estrarre distanze da un'immagine può essere complesso, poiché la precisione dipende da:

1. Fattori di distorsione: Le immagini possono essere affette da distorsioni ottiche, che devono essere corrette calibrando la camera utilizzando, ad esempio, una scacchiera di riferimento.
2. Effetto prospettico: La scala di riferimento varia con la distanza dal piano di acquisizione. Per oggetti posti a diverse profondità, è necessario applicare fattori di scala specifici, calcolati utilizzando un modello come quello della pin-hole camera.
3. Distorsioni prospettiche: Queste possono essere corrette utilizzando ottiche telecentriche, particolarmente utili per applicazioni che richiedono un'elevata accuratezza, come nelle misurazioni spaziali o bioingegneristiche.

Con questa premessa, il fattore di scala utilizzato nel nostro studio rappresenta un'approssimazione valida nel contesto specifico delle immagini 2D acquisite in condizioni controllate. Tuttavia, per applicazioni più rigorose, come quelle descritte sopra, è necessario considerare strumenti e metodi avanzati per la calibrazione.

Calcolo della Distanza tra i Punti

Le coordinate dei punti sono:

$Q_{2}(525.3,-406)$ e $R_{2}(764.4,-407.1)$

La formula per la distanza euclidea è:

$d={\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}}$

Sostituendo i valori:

$d={\sqrt {(764.4-525.3)^{2}+(-407.1-(-406))^{2}}}$

$d={\sqrt {(239.1)^{2}+(-1.1)^{2}}}$

$d={\sqrt {57121.81+1.21}}={\sqrt {57123.02}}\approx 239.02\,{\text{pixel}}$

Conversione della Scala in mm

Dato che sappiamo che il segmento di $239.02\,{\text{pixel}}$ equivale a $1\,{\text{cm}}=10\,{\text{mm}}$, calcoliamo la conversione in mm/pixel:

${\text{Scala in mm/pixel}}={\frac {\text{Lunghezza reale (in mm)}}{\text{Distanza in pixel}}}={\frac {10}{239.02}}\approx 0.04184\,{\text{mm/pixel}}$

Quindi, ogni pixel nella figura corrisponde a circa:

$0.04184\,{\text{mm/pixel}}$.

Esempio di Applicazione: Conversione Distanza in mm

Supponiamo di voler calcolare una distanza in mm. Ad esempio, se la distanza in pixel fosse $d=100\,{\text{pixel}}$:

$d_{\text{mm}}=100\cdot 0.04184\approx 4.184{\text{mm}}$

Risultato Finale

La scala è:

• $239.02\,{\text{pixel/cm}}$
• $0.04184{\text{mm/pixel}}$

Questi valori possono essere usati per convertire qualsiasi distanza misurata in pixel nella figura in unità metriche come millimetri o centimetri.

Cinematica dei Condili

Traslazioni e Rotazioni dei Condili

Nel contesto del movimento mandibolare, i condili non eseguono solo movimenti traslatori (spostamenti lineari nello spazio), ma anche rotatori (movimenti angolari attorno a specifici assi). Questo doppio movimento, noto come rototraslazione, è essenziale per comprendere la complessità della cinematica mandibolare.

Per descrivere in modo accurato la posizione e il movimento di ciascun condilo nel tempo, possiamo utilizzare un insieme di vettori di posizione. Questi vettori, che rappresentano i punti nel sistema di riferimento cartesiano, variano in modulo e direzione a seguito del moto elicoidale. Il moto può essere descritto combinando spostamenti lineari e variazioni angolari, che influenzano la posizione dei vettori stessi all'interno dello spazio tridimensionale.

Vettori di Posizione del Condilo Laterotrusivo (Lavorante)

Il condilo laterotrusivo si trova sul lato in cui avviene la laterotrusione, ovvero lo spostamento laterale della mandibola. Durante il movimento, la posizione del condilo può essere descritta mediante un vettore di posizione, definito come il segmento orientato che congiunge il condilo a un’origine del sistema di riferimento cartesiano scelto.Il vettore di posizione varia nel tempo sia in modulo che in direzione, a causa della natura complessa del moto elicoidale. Questo permette di rappresentare il movimento del condilo come una combinazione di spostamenti lineari e cambiamenti di orientamento nel sistema tridimensionale.

Il vettore di posizione del condilo laterotrusivo nel tempo è descritto da:

$P_{l}(t)=[X_{l}(t),Y_{l}(t),Z_{l}(t),\theta _{l}(t),\phi _{l}(t),\psi _{l}(t)]$

Dove:

• $X_{l}(t),Y_{l}(t),Z_{l}(t)$: Rappresentano gli spostamenti lineari del condilo laterotrusivo lungo i tre assi dello spazio cartesiano:
  • $X_{l}(t)$: Spostamento lungo l'asse antero-posteriore (avanti e indietro).
  • $Y_{l}(t)$: Spostamento lungo l'asse latero-mediale (lateralizzazione destra e sinistra).
  • $Z_{l}(t)$: Spostamento lungo l'asse verticale (alto e basso)
  • $\theta _{l}(t)$, $\phi _{l}(t)$, $\psi _{l}(t)$: Sono le rotazioni angolari del condilo laterotrusivo attorno ai tre assi del sistema di riferimento cartesiano scelto. Queste rotazioni rappresentano il cambiamento di orientamento del condilo nello spazio, descritto utilizzando la convenzione degli angoli di Eulero. È fondamentale notare che le rotazioni non sono commutative, e quindi l'ordine in cui avvengono le rotazioni deve essere specificato per garantire una descrizione univoca.

Nel nostro caso, adottiamo la convenzione $X,Y,Z$ che descrive le rotazioni nel seguente ordine:

• $\theta _{l}(t)$: Rotazione attorno all'asse $x$ (causa una torsione laterale della mandibola).

• $\phi _{l}(t)$: Rotazione attorno all'asse $y$ (controlla l'apertura e la chiusura della mandibola).

• $\psi _{l}(t)$: Rotazione attorno all'asse $z$ (controlla la rotazione laterale/mediale della mandibola).

Questa sequenza di rotazioni consente di determinare in modo univoco l'orientamento del condilo nello spazio, evitando ambiguità derivanti dalla non-commutatività delle rotazioni angolari.

• Sirignathograph rotazione asse Y.jpg

  Figura 2: Rappresentazione dei tracciati cinematici masticatori sul piano sagittale

• 

  Figura 2: Rappresentazione dei tracciati cinematici masticatori sul piano sagittale

• 

  Figura 3: Rappresentazione dei tracciati cinematici masticatori sul piano coronale

• 

  Figura 4: Rappresentazione dei tracciati cinematici masticatori sul piano assiale

Ovviamente, la stessa procedura geometrica matematica impiegata per il condilo laterotrusivo sarà utilizzata anche per il condilo mediotrusivo ma noteremo delle caratteristiche essenziali che descrivo il fenomeno laterotrusivo dal mediotrusivo ed i corrispottivi tracciati condizionati sulle aree occlusali.

Questa prima descrizione rappresenta solo il primo livello di complessità perchè i movimenti dei condili laterotrusivo e mediotrusivo si influenzano reciprocamente durante i cicli masticatori. Il condilo laterotrusivo esegue una rototraslazione lungo un arco che descrive una combinazione di rotazione attorno all'asse verticale $_{v}HA$ ed uno spostamento laterale. Al contrario, il condilo mediotrusivo si sposta principalmente medialmente e anteriormente. Descriviamone la dinamica

La rotazione del condilo laterotrusivo attorno all'asse $Z$ (verticale) è descritta matematicamente utilizzando una trasformazione lineare nel piano trasversale $(X,Y)$. Questa trasformazione è rappresentata dalla seguente matrice di rotazione:

$R_{\psi }={\begin{pmatrix}\cos(\psi )&-\sin(\psi )\\\sin(\psi )&\cos(\psi )\end{pmatrix}}\cdot {\begin{pmatrix}X_{L}\\Y_{L}\end{pmatrix}}$

Dove:

• $\psi$ rappresenta l'angolo di rotazione attorno all'asse $Z$ (asse verticale).
• $(X_{L},Y_{L})$ sono le coordinate del condilo laterotrusivo nel piano trasversale.

Questo descrive il cambiamento di posizione del condilo laterotrusivo nel piano $(X,Y)$ dovuto alla rotazione angolare.

Il condilo mediotrusivo, invece, si muove principalmente con una traslazione nello spazio tridimensionale, lungo i piani trasversale e sagittale, generando un tragitto noto come "Tragitto orbitante". La traslazione è descritta dal seguente vettore:

$T_{M}(t)={\begin{pmatrix}X_{M}(t)\\Y_{M}(t)\\Z_{M}(t)\end{pmatrix}}$

Dove:

• $(X_{M}(t),Y_{M}(t),Z_{M}(t))$ rappresentano le coordinate temporali del condilo mediotrusivo nello spazio cartesiano tridimensionale.

Questa traslazione rappresenta il movimento anteriore e mediale del condilo mediotrusivo principalmente lineare ed è per questo che non compare la matrice rotazionale ma potrebbe anche incorporare una rotazione attorno all'asse $Z$ (asse verticale) influenzando significativamente la dinamica complessiva del ciclo masticatorio. Questo tipo di rotazine aggiuntiva al fenomeno orbitante è difficile da comprendere perchè è di minima entità angolare ma vedremo, in seguito, l'influenza che ha sui tracciati occlusali.

Descrizione delle misure lineari ed angolari

Rappresentazione scalare dei tracciati condilari

Descrizione delle distanze e delle direzioni

Di seguito sono riportate le distanze calcolate tra i punti rispetto al punto di partenza (punto 1, massima intercuspidazione) considerato punto di riferimento e le relative direzioni nello spazio, utilizzando le coordinate corrette per gli assi $X$ (antero-posteriore) e $Y$ (latero-mediale).

Calcolo delle distanze tra i punti

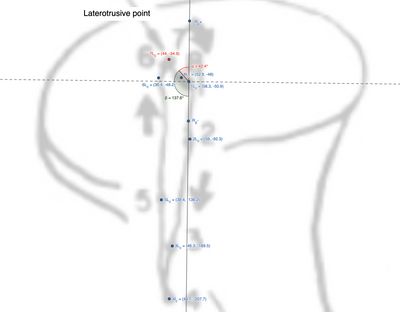
Le coordinate dei punti estrapolate da Geogebra dopo calibrazione, per il condilo laterotrusivo, sono:

1L: $(58.3,-50.9)$

2L: $(59,-92.3)$

3L: $(46.3,-169.5)$

4L: $(44.1,-207.7)$

5L: $(38.4,-136.2)$

6L: $(36.4,-48.2)$

7L: $(44,-34.9)$

8L: $(52.9,-48)$

Fattore di scala: $0.04184\,{\text{mm/pixel}}$

Distanze rispetto a $1L_{c}$

$2L_{c}$

$d={\sqrt {(59-58.3)^{2}+(-92.3-(-50.9))^{2}}}={\sqrt {(0.7)^{2}+(-41.4)^{2}}}={\sqrt {0.49+1714.36}}\approx 41.41\,{\text{pixel}}$

$d=41.41\cdot 0.04184\approx 1.734\,{\text{mm}}$

$3L_{c}$

$d={\sqrt {(46.3-58.3)^{2}+(-169.5-(-50.9))^{2}}}={\sqrt {(-12)^{2}+(-118.6)^{2}}}={\sqrt {144+14063.96}}\approx 119.17\,{\text{pixel}}$

$d=119.17\cdot 0.04184\approx 4.99\,{\text{mm}}$

$4L_{c}$

$d={\sqrt {(44.1-58.3)^{2}+(-207.7-(-50.9))^{2}}}={\sqrt {(-14.2)^{2}+(-156.8)^{2}}}={\sqrt {201.64+24589.44}}\approx 157.43\,{\text{pixel}}$

$d=157.43\cdot 0.04184\approx 6.59\,{\text{mm}}$

$5L_{c}$

$d={\sqrt {(38.4-58.3)^{2}+(-136.2-(-50.9))^{2}}}={\sqrt {(-19.9)^{2}+(-85.3)^{2}}}={\sqrt {396.01+7275.09}}\approx 87.6\,{\text{pixel}}$

$d=87.6\cdot 0.04184\approx 3.66\,{\text{mm}}$

$6L_{c}$

$d={\sqrt {(36.4-58.3)^{2}+(-48.2-(-50.9))^{2}}}={\sqrt {(-21.9)^{2}+(2.7)^{2}}}={\sqrt {479.61+7.29}}\approx 22.06\,{\text{pixel}}$ $d=22.06\cdot 0.04184\approx 0.923\,{\text{mm}}$

$7L_{c}$

$d={\sqrt {(44-58.3)^{2}+(-34.9-(-50.9))^{2}}}={\sqrt {(-14.3)^{2}+(16)^{2}}}={\sqrt {204.49+256}}\approx 21.47\,{\text{pixel}}$ $d=21.47\cdot 0.04184\approx 0.898\,{\text{mm}}$

$8L_{c}$

$d={\sqrt {(52.9-58.3)^{2}+(-48-(-50.9))^{2}}}={\sqrt {(-5.4)^{2}+(2.9)^{2}}}={\sqrt {29.16+8.41}}\approx 6.13\,{\text{pixel}}$

$d=6.13\cdot 0.04184\approx 0.257\,{\text{mm}}$

Condilo Laterotrusivo

Questo paragrafo illustra un processo matematico per calcolare la distanza e l'angolo formato tra due segmenti in un piano 2D, con applicazione nella cinematica mandibolare. La spiegazione riguarda il calcolo degli angoli tra vettori che rappresentano movimenti articolari, ad esempio i condili durante i movimenti mandibolari (Figura 5 e Tabella 1).

Tabella 1
Tracciato masticatorio	Markers	Distanza (mm)	Direzione $X$	Direzione $Y$
Figura 5: Sovrapposizione dei marker in Geogebra nel tracciato cinematico del condilo laterotrusivo	2	1.734	Protrusiva	Parallela
	3	4.99	Protrusiva	Lateralizzazione
	4	6.59	Protrusiva	Lateralizzazione
	5	3.66	Inversione	Inversione
	6	0.923	Retrusiva	Lateralizzazione
	7*	0.898	Protrsiva	Medializzazione
	8	0.257	Protrusiva	Medializzazione

Osservando la figura e la tabella, possiamo estrapolare le distanze tra i punti marcati ed in particolare segnaliamo che è stato considerato il punto $7L_{c}$ come punto estremo in cui il condilo inverte il moto ed inizia un percorso mediali verso la massima intercuspidazione. Questo punto, anzi, la distanza tra questo punto ed il punto $1L_{c}$ rappresenta il movimento di Bennett. Ad esempio, questa distanza è stata correttamente calcolata come circa $0.898\,_{\text{mm}}$ con una direzione calcolata come:

$\theta =131.87^{\circ }$ ed il corrispettivo $\theta ^{'}=42^{\circ }$

Per chi desidera approfondire il formalismo matematico, riportiamo il calcolo dettagliato nel popup interattivo. Calcolo dettagliato: distanza tra $P_{1}=(58.3,-50.9)$ e $P_{7}=(44,-34.9)$, distanza euclidea ${\sqrt {(-14.3)^{2}+(16)^{2}}}\approx 21.47\,{\text{pixel}}$, convertita in mm come $21.47\times 0.04184\approx 0.898\,{\text{mm}}$, angolo $\theta =\arccos(-0.6665)\approx 131.87^{\circ }$.

---

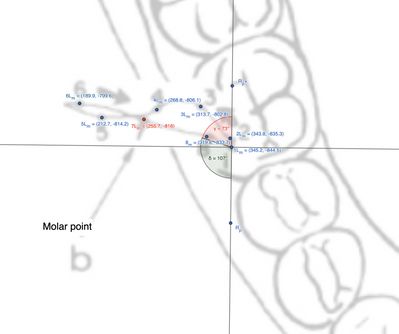
Molare Laterotrusivo

Il testo descrive un'analisi dettagliata dei movimenti articolari del molare ipsilaterale al condilo laterotrusivo (Figura 6 e Tabella 2). L'analisi si basa sul calcolo delle distanze tra punti e degli angoli formati tra i vettori utilizzando la trigonometria vettoriale.

Tabella 2
Tracciato masticatorio	Markers	Distanza (mm)	Direzione $X$	Direzione dinamica $Y$
Figura 6: Rappresentazione grafica dei markers rilevati dal 'Replicator' nella masticazione sul lato destro del paziente	2	0.39	Indietro	Lateralizzazione
	3	2.18	Indietro	Lateralizzazione
	4	3.57	Indietro	Lateralizzazione
	5	5.68	Indietro	Lateralizzazione
	6	6.76	Indietro	Inversione
	7*	3.93	Indietro	Medializzazione
	8	1.15	Indietro	Medializzazione

Osservando la figura e la tabella, possiamo estrapolare le distanze e le direzioni dei punti marcati. Nello specifico, la distanza del punto $7L_{m}$ rispetto al punto iniziale $1L_{m}$ è stata calcolata come circa $3.93\,_{\text{mm}}$, con un angolo formato tra i vettori pari a $\cong 73^{\circ }$. Definizione dei vettori:${\vec {AB}}=7L_{m}-1L_{m}=(255.7,-816.0)-(345.2,-844.5)=(-89.5,28.5)$, ${\vec {AC}}=R_{p}-1L_{m}=(346.6,-727.1)-(345.2,-844.5)=(1.4,117.4)$. Magnitudine di ${\vec {AB}}$: $|{\vec {AB}}|={\sqrt {(-89.5)^{2}+(28.5)^{2}}}\approx 93.93$, magnitudine di ${\vec {AC}}$: $|{\vec {AC}}|={\sqrt {(1.4)^{2}+(117.4)^{2}}}\approx 117.41$. Prodotto scalare: ${\vec {AB}}\cdot {\vec {AC}}=(-89.5)(1.4)+(28.5)(117.4)=2928.4$, $\cos(\theta )={\frac {{\vec {AB}}\cdot {\vec {AC}}}{|{\vec {AB}}|\cdot |{\vec {AC}}|}}={\frac {2928.4}{93.93\cdot 117.41}}\approx 0.292$, angolo: $\theta =\arccos(0.292)\approx 73.02^{\circ }$

---

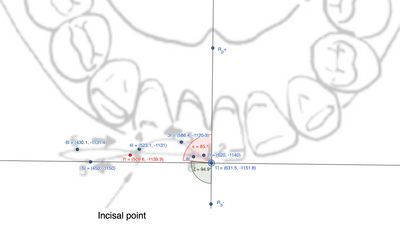
Incisal

Il paragrafo descrive un'analisi matematica dei movimenti articolari dell'incisivo sul lato lavorante. Utilizzando le coordinate di tre punti nello spazio 2D $1_{I}$, $7_{I}$ e ${R_{p}}^{+}$, vengono calcolate le distanze lineari tra i punti, oltre all'angolo tra i segmenti che collegano questi punti.

Tabella 3
Tracciato masticatorio	Markers	Distanza (mm)	Direzione $X$	Direzione dinamica $Y$
Figura 7: Rappresentazione grafica dei markers rilevati dal 'Replicator' nella masticazione sul lato destro del paziente nell'area inccisale.	2	0.69	Retrusiva	Lateralizzazione
	3	2.30	Retrusiva	Lateralizzazione
	4	4.61	Retrusiva	Lateralizzazione
	5	7.58	Protrusivo	Lateralizzazione
	6	8.54	Retrusiva	Inversione
	7*	5.12	Retrusiva	Medializzazione
	8	1.75	Retrusiva	Medializzazione

Per quanto riguarda i tracciati nell'area dell'incisivo tra il punto $1I$ e $7I$, la distanza risulta essere di $5.12_{mm}$ con un angolo approssimativamente pari a $85.1^{\circ }$. Per approfondimenti di calcolo, vedi la spiegazione dettagliata qui  Coordinate dei punti: $1I=(631.5,-1151.8)$, $7I=(509.6,-1139.9)$, $R_{p}^{+}=(634.3,-912.8)$. Vettori: ${\vec {1I7I}}=(-121.9,11.9)$, ${\vec {1IR_{p}^{+}}}=(2.8,239)$. Norme: $|{\vec {1I7I}}|=122.49$, $|{\vec {1IR_{p}^{+}}}|=238.95$. Prodotto scalare: ${\vec {1I7I}}\cdot {\vec {1IR_{p}^{+}}}=2502.78$. Coseno: $\cos(\theta )={\frac {2502.78}{122.49\cdot 238.95}}\approx 0.0855$. Angolo: $\theta =\arccos(0.0855)\approx 85.1^{\circ }$.

---

Molare mediotrusivo

Osservando il moto cinematico mandibolare a livello del molare mediotrusivo, si nota il cambiamento di direzione angolare rispetto al molare laterotrusivo ($73^{\circ }$) ed all'incisivo ($85^{\circ }$). Angolo che tende ad aumentare fino a raggiungere il massimo a livello del condilo ($180^{\circ }$). L'angolo così formato è conosciuto come angolo di svincolo mediotrusivo tra la cuspide centrale e distale del primo molare.La tabella 4 mostra le distanze tra i punti del tracciato ed il punto $1M_{m}$.

Tabella 4
Tracciato mediotrusivo molare	Markers	Distanza (mm)	Direzione $X$	Direzione dinamica $Y$
Figura 8: Rappresentazione grafica dei markers rilevati dal 'Replicator' nella masticazione sul lato destro del paziente nell'area inccisale.	2	0.68	Retrusiva	Medializzazione
	3	2.19	Retrusiva	Medializzazione
	4	3.22	Retrusiva	Medializzazione
	5	5.79	Protrusiva	Medializzazione
	6	7.22	Protrusiva	Inversione
	7*	4.81	Retrusiva	Lateralizzazione
	8	1.18	Retrusiva	Lateralizzazione

Come per i precedenti, la distanza lineare tra il punto $1M_{m}$ ed il punto $7M_{m}$ è risultata essere $4.81_{mm}$ mentre l'angolo è stato calcolato come:$\theta =\arccos(0.0226)\approx 91.33^{\circ }$ Per approfondire la procedura matematica, vedi la spiegazione dettagliata qui Definizione vettori ${\vec {1M_{m}7M_{m}}}=(818.8-910.7,-855.1-(-856.2))=(-91.9,1.1)$,${\vec {1M_{m}R_{p}^{+}}}=(912-910.7,-741.2-(-856.2))=(1.3,115)$. Prodotto scalare: ${\vec {1M_{m}7M_{m}}}\cdot {\vec {1M_{m}R_{p}^{+}}}=(-91.9\cdot 1.3)+(1.1\cdot 115)=-119.47+126.5=7.03$. Norme:$|{\vec {1M_{m}7M_{m}}}|={\sqrt {(-91.9)^{2}+(1.1)^{2}}}\approx 91.92$, $|{\vec {1M_{m}R_{p}^{+}}}|={\sqrt {(1.3)^{2}+(115)^{2}}}\approx 115.02$. Coseno: $\cos(\theta )={\frac {7.03}{91.92\cdot 115.02}}\approx 0.000665$. Angolo: $\theta =\arccos(0.000665)\approx 90^{\circ }$.

---

Condilo Mediotrusivo

Questi punti rappresentano posizioni specifiche all'interno di un sistema articolare che stiamo studiando, con l'obiettivo di calcolare l'angolo tra il segmento che unisce i punti $1M_{c}$ e $/M_{c}$, e il segmento che unisce i punti $1M_{c}$ e $R_{p}c$. Questo tipo di analisi è comune nella modellazione di movimenti articolari per comprendere come si muovono i segmenti di un sistema rispetto a un punto di riferimento, come nel caso di un sistema masticatorio.

Tabella 5
Tracciato masticatorio	Markers	Distanza (mm)	Direzione $X$	Direzione $Y$
Figura 9: Rappresentazione grafica dei markers rilevati dal 'Replicator'nella masticazione sul lato destro del paziente nell'area inccisale.	2	2.13	Protrusiva	Medializzazione
	3	6.19	Protrusiva	Medializzazione
	4	10.70	Protrusiva	Medializzazione
	5	11.09	Protrusiva	Inversione
	6	6.09	Protrusiva	Lateralizzazione
	7*	2.61	Protrusiva	Lateralizzazione
	8	0.50	Protrusiva	Lateralizzazione

Per quanto riguarda le distanze e la direzione del punto 7 nel condilo mediotrusivo, abbiamo una distanza dal punto di partenza di $6.88$mm ed un angolo calcolato sull'arcoseno $\theta =\arccos(-0.971)\approx 166^{\circ }$. Infine, sottraendo questo angolo da 180°, otteniamo un angolo di $14^{\circ }$, noto come Angolo di Bennett. Per approfondire la procedura matematica, vedi  Calcolo sintetico: vettore ${\vec {AB}}=(-15.9,-60.4)$, vettore${\vec {AC}}=(0.2,52.5)$, prodotto scalare ${\vec {AB}}\cdot {\vec {AC}}=-3172.62$, norme $|{\vec {AB}}|=62.93$, $|{\vec {AC}}|=52.50$, $\cos(\theta )={\frac {-3172.62}{62.93\cdot 52.50}}\approx -0.971$, $\theta =\arccos(-0.971)\approx 166^{\circ }$.

---

Discussione sulla rototraslazione condilari

Il moto rototraslazionale dei condili è fondamentale per comprendere la cinematica mandibolare e i tracciati descritti dai denti durante la masticazione. Se i condili ruotassero semplicemente attorno a un punto fisso, i tracciati dei molari e degli incisivi sarebbero archi di cerchio con un unico centro. Tuttavia, i movimenti reali dei condili sono molto più complessi.

Durante la laterotrusione, il condilo ipsilaterale (dello stesso lato) esegue un movimento che combina rotazione attorno all'asse verticale e traslazione laterale. Allo stesso tempo, il condilo controlaterale si muove principalmente in direzione mediale e anteriore, descrivendo un percorso noto come "Tragitto orbitante".

Descrizione matematica

Matematicamente, possiamo descrivere il moto rototraslazionale del condilo laterotrusivo come una combinazione di una rotazione attorno all'asse verticale passante per il condilo stesso e una traslazione laterale lungo una traiettoria specifica. La posizione del molare ipsilaterale in un determinato istante può essere ottenuta applicando la rotazione attorno all'asse verticale e poi la traslazione corrispondente:

$x_{m}=x_{m0}\cos(\theta )-y_{m0}\sin(\theta )+T_{x}$

$y_{m}=x_{m0}\sin(\theta )+y_{m0}\cos(\theta )$

Dove:

• $(x_{m0},y_{m0})$ è la posizione iniziale del molare ipsilaterale.
• $T_{x}$ rappresenta la traslazione laterale lungo l'asse $x$.
• $(x_{m},y_{m})$ rappresenta la posizione finale del molare ipsilaterale.

Man mano che il condilo ruota e si sposta lateralmente, le coordinate $(x_{m},y_{m})$ del molare descrivono una traiettoria ellittica proiettata su un piano bidimensionale. Questo fenomeno ellittico si verifica perché il centro di rotazione istantaneo del condilo laterotrusivo non è fisso, ma si sposta continuamente a causa della traslazione laterale. Pertanto, il tracciato descritto dal molare ipsilaterale non può essere un semplice arco di cerchio, ma assume una forma ellittica.

Un comportamento simile si osserva anche per il condilo controlaterale (mediotrusivo) e per gli incisivi. Sebbene il movimento del condilo mediotrusivo sia principalmente una traslazione mediale e anteriore, può essere coinvolta anche una certa rotazione attorno all'asse verticale. Questa combinazione di traslazione e rotazione porta nuovamente a tracciati ellittici per il molare controlaterale e per gli incisivi.

È importante sottolineare che i tracciati ellittici osservati non sono ellissi perfette, ma curve più complesse, poiché i movimenti dei condili non sono semplici rotazioni e traslazioni costanti. Infatti, i condili seguono traiettorie più elaborate, con accelerazioni e decelerazioni, che si riflettono nella forma dei tracciati dei denti.

Inoltre, i tracciati dei molari e degli incisivi non sono indipendenti, ma sono strettamente correlati ai movimenti dei condili corrispondenti. Pertanto, l'analisi dei tracciati dei denti può fornire informazioni preziose sulla cinematica mandibolare e sui movimenti articolari dei condili.

Figura 10a: Rappresentazione generica di conica, segue descrizione dettagliata.

In conclusione, la combinazione di rotazione e traslazione dei condili durante i movimenti mandibolari impedisce ai tracciati dei molari e degli incisivi di essere semplici archi di cerchio. Invece, questi tracciati assumono forme ellittiche, poiché il centro di rotazione istantaneo dei condili si sposta continuamente a causa del moto rototraslazionale complesso. Per comprendere meglio la complessità delle traiettorie, è stato costruito un modello matematico basato su una conica passante per cinque punti strategicamente scelti, come illustrato nella figura 10a e approfondito nel prossimo paragrafo.

Rappresentazione cinematica attraverso una conica

Per rappresentare in modo più dettagliato e formale la forma ellittica dei tracciati dei denti dovuti al moto rototraslazionale dei condili, possiamo sovrapporre una conica (ellisse) a più punti. Questo ci permetterà di evidenziare il contributo dei movimenti dei condili laterotrusivo e mediotrusivo, nonché delle distanze occlusali da essi, nella generazione di tali tracciati pseudoellittici.

Consideriamo ad esempio il tracciato del molare ipsilaterale durante la laterotrusione. Supponiamo di avere le coordinate di 5 punti distinti su questo tracciato: $(x_{1},y_{1}),(x_{2},y_{2}),(x_{3},y_{3}),(x_{4},y_{4}),(x_{5},y_{5})$.

L'equazione generale di un'ellisse centrata nell'origine è data da:

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1$

Dove $a$ e $b$ sono rispettivamente i semiassi maggiore e minore dell'ellisse.

Per determinare i valori di $a$ e $b$ che meglio approssimano i 5 punti dati, possiamo utilizzare il metodo dei minimi quadrati. L'obiettivo è minimizzare la somma dei quadrati delle distanze dei punti dall'ellisse.

Definiamo la funzione di costo:

$J(a,b)=\sum _{i=1}^{5}\left[\left({\frac {x_{i}^{2}}{a^{2}}}+{\frac {y_{i}^{2}}{b^{2}}}-1\right)^{2}\right]$

Minimizzando $J(a,b)$ rispetto a $a$ e $b$, otteniamo le stime ottimali dei semiassi $a$ e $b$ che approssimano al meglio i punti dati.

Questa ellisse ottimizzata rappresenterà il tracciato pseudoellittico del molare ipsilaterale, influenzato dai movimenti rototraslazionali dei condili laterotrusivo e mediotrusivo, nonché dalle distanze occlusali da essi.

I semiassi $a$ e $b$ dell'ellisse saranno determinati dai pesi relativi dei contributi dei condili e delle distanze occlusali. Ad esempio, un valore di $a$ maggiore potrebbe indicare un'influenza più significativa del condilo laterotrusivo, mentre un valore di $b$ più piccolo potrebbe suggerire un'influenza minore del condilo mediotrusivo o delle distanze occlusali.

Questo approccio può essere applicato anche ai tracciati degli incisivi e dei molari controlaterali, sovrapponendo ellissi ottimizzate ai rispettivi punti per ottenere una rappresentazione formale dei loro tracciati pseudoellittici.

In questo modo, l'analisi matematica dei tracciati dei denti durante la masticazione può essere arricchita con una rappresentazione visiva più dettagliata e quantitativa, permettendo di studiare in modo più approfondito il contributo dei diversi fattori cinematici, come i movimenti dei condili e le distanze occlusali, nella generazione di tali tracciati complessi.

La scelta della conica a 5 punti

La scelta di una conica a 5 punti rappresenta un approccio matematico e geometrico efficace per modellare i tracciati articolari reali rispetto a un'ellisse ideale.

Definizione della conica

Una conica è una curva definita in geometria analitica come il luogo dei punti che soddisfano un'equazione quadratica generale:$Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0$

Dove:

• $A,B,C,D,E,F$ sono coefficienti reali determinati dai punti dati.

La forma della conica (ellisse, parabola o iperbole) dipende dal discriminante:

• Ellisse se $B^{2}-4AC<0$
• Parabola se $B^{2}-4AC=0$
• Iperbole se $B^{2}-4AC>0$

Perché 5 punti?

Una conica è univocamente determinata da 5 punti distinti e non allineati. Questo significa che se conosci 5 punti sperimentali, puoi ricostruire una sola conica che passa per quei punti.

• Univocità: La conica è unica per 5 punti non allineati.
• Adattabilità: Si adatta meglio ai dati sperimentali rispetto a un'ellisse ideale.
• Flessibilità: Modella tracciati complessi, asimmetrici o irregolari, tipici della cinematica mandibolare.

Costruzione delle coniche specifiche

Abbiamo costruito coniche specifiche per diverse aree della traiettoria mandibolare e, comunque, a secondo di cosa si vuole analizzare l'ordine dei punti prescelti può essere cambiato:

Conica del molare laterotrusivo

La conica è stata costruita utilizzando 5 punti chiave lungo il tracciato sperimentale del molare laterotrusivo

• $P_{1}=(68.3,-50.9)$
• $P_{2}=(58.3,-50.9)$
• $P_{3}=(345.2,-844.5)$
• $P_{4}=(255.7,-816)$
• $P_{5}=(509.6,-1139.9)$

Conica dell'incisivo

La conica è stata determinata utilizzando punti significativi lungo la traiettoria reale dello '<<<Incisivo':

• $P_{1}=(509.6,-1139.9)$
• $P_{2}=(631.5,-1151.8)$
• $P_{3}=(68.3,-50.9)$
• $P_{4}=(58.3,-50.9)$
• $P_{5}=(910.7,-856.2)$

Conica del molare mediotrusivo

La conica è stata generata per il 'molare mediotrusivo' usando i seguenti punti chiave:

$P_{1}=(910.7,-856.2)$

• $P_{2}=(818.8,-855.1)$
• $P_{3}=(68.3,-50.9)$
• $P_{4}=(58.3,-50.9)$
• $P_{5}=(345.2,-844.5)$

Costruzione della conica unificata

Per ottenere una visione complessiva (Fig.7b), si è calcolato una 'conica unificata' a partire dalle coniche specifiche. Questa conica è stata costruita mediando i coefficienti delle coniche delle diverse aree:

${\text{Coefficienti Conica Unificata}}={\frac {{\text{Coeff}}_{\text{molare laterotrusivo}}+{\text{Coeff}}_{\text{incisale}}+{\text{Coeff}}_{\text{molare mediotrusivo}}+{\text{Coeff}}_{\text{condilo mediotrusivo}}}{4}}$

L'equazione risultante è:

$Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0$

(dove i coefficienti verranno calcolati sulla base dei punti definitivi).

Figura 7b: Rappresentazione della conica passante per 5 punti strategicamente scelti come descritto nel testo. Notare la discrepanza tra i vettori ed il passaggio della conica che indica il diverso condizionamento della componente traslatoria da quella rotatoria. Effetto che si nota maggiormente sul molare mediotrusivo.

Applicazione della conica per individuare punti cinematici

Utilizzando la conica del molare laterotrusivo, è possibile 'prevedere il punto $7L_{c}$ (condilo laterotrusivo) conoscendo due punti di riferimento (es. punto iniziale e finale sul tracciato molare). Questo approccio permette di determinare con precisione dove cade il punto condilare laterotrusivo sulla conica e utilizzare la conica come strumento per analizzare deviazioni e adattamenti nei tracciati mandibolari reali.

Discussione e Conclusioni

Discussione sulla Rototraslazione Condilare e Tracciati Masticatori

La cinematica mandibolare è il risultato della complessa interazione tra i movimenti dei condili e i tracciati occlusali dei denti, analizzabili tramite i dati geometrici e cinematici. Ogni punto del sistema mandibolare (condili, molari, incisivi) segue traiettorie specifiche che riflettono la dinamica articolare e la relazione occlusale. L'obiettivo di questa discussione è fornire al lettore una comprensione delle correlazioni tra i tracciati condilari e dentali, nonché delle implicazioni cliniche.

Relazione tra Condilo Laterotrusivo e Tracciati Occlusali

Il condilo laterotrusivo rappresenta il lato lavorante e segue un tracciato combinato di rotazione e traslazione laterale. Le distanze e gli angoli calcolati (es. movimento di Bennett, distanza $1L_{c}-7L_{c}$ pari a $0.898\,{\text{mm}}$) dimostrano che il condilo cambia direzione durante il movimento masticatorio, invertendo il moto da protrusivo a retrusivo. Questo cambio di direzione corrisponde a una "inversione" dei tracciati occlusali, visibile anche nel molare ipsilaterale e negli incisivi.

La figura e la tabella associata dimostrano che i tracciati del condilo laterotrusivo influenzano la distribuzione delle forze occlusali. Ad esempio, il punto estremo del condilo ($7L_{c}$) rappresenta un'importante transizione biomeccanica, che può essere utilizzata clinicamente per valutare la stabilità articolare e la simmetria funzionale.Si tenga conto che una pposizione di massima retrusione masticatoria è generata quasi esclusivamente dal muscolo temporale che ha una funzione di chiusura, lateralizzazione e retrusione mandibolare. In sostanza più si masticano cibo du elevata durezza più si sposta posteriormente e la chiusura masticatoria diventa lateroretrusiva.

Dinamica dei Molari Ipsilaterali

I molari ipsilaterali al condilo laterotrusivo seguono un tracciato coerente con il moto condilare, ma la loro traiettoria riflette una maggiore interazione con i punti di contatto occlusali. Come evidenziato nella Tabella 2, i molari mostrano un graduale spostamento laterale con una successiva medializzazione nel punto $7L_{m}$, in cui si osserva un angolo di circa $73^{\circ }$.

Analisi degli Incisivi e la Transizione Occlusale

Gli incisivi laterotrusivi presentano tracciati che combinano retrusione e lateralizzazione. La distanza $1I-7I$ di $5.12\,{\text{mm}}$ con un angolo $\theta \approx 85.1^{\circ }$ sottolinea una progressiva convergenza verso la massima intercuspidazione. Clinicamente, ciò suggerisce che gli incisivi lavorano come guida durante i movimenti laterali, trasferendo il carico occlusale ai molari mediotrusivi.

Correlazione con il Condilo Mediotrusivo

Il condilo mediotrusivo, che rappresenta il lato bilanciante, segue un tracciato con una combinazione di traslazione mediale e rotazione limitata. La distanza $1M_{c}-7M_{c}$ di $2.61\,{\text{mm}}$ e un angolo $\theta \approx 166^{\circ }$ evidenziano un movimento più controllato rispetto al condilo laterotrusivo. Questa traiettoria è strettamente correlata con i tracciati del molare mediotrusivo, che seguono una direzione prevalentemente medializzante.

La dinamica del molare mediotrusivo, come mostrato nella Tabella 4, rivela un'inversione della direzione al punto $6M_{m}$, evidenziando una transizione critica per il bilanciamento delle forze masticatorie. Questo comportamento si collega direttamente al ruolo del condilo mediotrusivo nel controllo della traiettoria occlusale e della stabilità articolare.

Implicazioni Cliniche

L'analisi delle correlazioni tra tracciati condilari e occlusali permette di identificare anomalie biomeccaniche e disfunzioni articolari. Ad esempio:

• Un angolo di Bennett eccessivo ($\theta >20^{\circ }$) potrebbe indicare instabilità articolare o ipermobilità condilare.
• Tracciati irregolari degli incisivi o dei molari possono riflettere asimmetrie muscolari o disfunzioni occlusali.

Questi dati possono essere utilizzati per ottimizzare i trattamenti protesici e ortodontici, garantendo una migliore distribuzione delle forze occlusali e una riduzione del rischio di disordini temporomandibolari.

In conclusione la cinematica mandibolare è una rete complessa di rotazioni, traslazioni e interazioni occlusali. L'analisi combinata dei tracciati condilari e dentali offre una comprensione dettagliata della dinamica masticatoria, fornendo strumenti diagnostici essenziali per migliorare la funzione e la stabilità articolare. La costruzione di un modello matematico basato su dati cinematici, come illustrato nelle figure e tabelle, rappresenta un importante passo avanti nella comprensione della biomeccanica mandibolare.

---

Discussione sul 'Residuo' dei vettori-conica

La costruzione delle coniche a 5 punti ha permesso di modellare con precisione i tracciati sul Molare laterotrusivo, Incisivo e Molare mediotrusivo. L'uso della 'Conica Unificata' ha offerto una visione globale, ma per una maggiore precisione, le 'coniche specifiche' risultano più adatte per localizzare punti chiave come il punto $7L_{c}$.

Vettore molare laterotrusivo ipsilaterale

Il molare 'laterotrusivo ipsilaterale' mostra un comportamento quasi coincidente con il passaggio della conica. Questo fenomeno si spiega con la 'relazione diretta tra il condilo laterotrusivo e il molare ipsilaterale', poiché la 'rotazione del condilo laterotrusivo' attorno all'asse verticale produce una traiettoria ellittica regolare e la traslazione del condilo laterotrusivo lungo una traiettoria definita genera variazioni che rimangono vincolate alla conica. Matematicamente, considerando la conica com$Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0$

e il vettore posizione del molare laterotrusivo come $\mathbf {r} _{L_{m}}(t)=(x_{L_{m}}(t),y_{L_{m}}(t))$il discostarsi del vettore è determinato dal residuo:

$R_{L_{m}}=A(x_{L_{m}})^{2}+Bx_{L_{m}}y_{L_{m}}+C(y_{L_{m}})^{2}+Dx_{L_{m}}+Ey_{L_{m}}+F$

Essendo $R_{L_{m}}\approx 0$, il vettore segue quasi perfettamente il passaggio della conica.

Vettore molare controlaterale (mediotrusivo)

Il molare 'controlaterale' (mediotrusivo) si discosta maggiormente dalla conica. Questo fenomeno si verifica perché il condilo compie un movimento prevalentemente traslatorio con una componente minima di rotazione e la traiettoria del molare controlaterale risente delle variazioni angolari complesse del condilo mediotrusivo, generando deviazioni dal piano della conica. Geometricamente, la traiettoria del molare mediotrusivo non segue perfettamente la conica a causa delle componenti traslazionali che deviano il tracciato rispetto alla curva ellittica ideale.

Matematicamente, il residuo per il molare mediotrusivo dato da$R_{M_{m}}=A(x_{M_{m}})^{2}+Bx_{M_{m}}y_{M_{m}}+C(y_{M_{m}})^{2}+Dx_{M_{m}}+Ey_{M_{m}}+F$

con$|R_{M_{m}}|>|R_{L_{m}}|$dimostra un maggiore scostamento rispetto alla conica.

Vettore incisale

Il vettore incisale si colloca in una posizione intermedia rispetto ai molari ipsilaterali e controlaterali. Questo perchè gli 'incisivi' sono influenzati dalla combinazione dei movimenti del condilo laterotrusivo e del condilo mediotrusivo. La traiettoria degli incisivi segue una curva regolare ma leggermente deviata rispetto alla conica. Matematicamente,il residuo per il vettore incisale è dato da$R_{I}=A(x_{I})^{2}+Bx_{I}y_{I}+C(y_{I})^{2}+Dx_{I}+Ey_{I}+F$con$|R_{L_{m}}|<|R_{I}|<|R_{M_{m}}|$dimostrando che il vettore incisale si discosta più del molare ipsilaterale ma meno del molare controlaterale.

«C'è qualcosa che ancora non va?»
(......si certo è la nostra abitudine di osservare il sistema come una cinematica di un punto mentre dietro il fenomeno della magia della sfera condilare si celano altre verità)

In conclusione, se osserviamo i tracciati rilevati dal Replicator sul molare mediotrusivo possiamo verificare come il vettore con direzione $7M_{m}$ che sostanzialmente genera il solco mediotrusivo tra la cuspide centrale e distale del molare si discosta dalla ellisse generata dalla conica a 5 punti perchè è stato trascurata l'influenza che genera sul sistema cinematico la sfera condilare. Argomento che tratteremo al prossimo capitolo.

---

Bibliography & references