Asse Cerniera verticale

Home

Scientific project

Social project

Our story

Scientific community

Book index

Our network

Frisardi Masticationpedia Network

Fontana Masticationpedia Network

Ed. Lab

Donate

Contact

Change language

German

Spanish

French

Italian

Asse Cerniera verticale

 

Article by  Gianni Frisardi

 

Introduzione

Nel capitolo precedente, 'Transverse Hinge Axis', abbiamo introdotto la cinematica mandibolare concentrandoci sul piano sagittale. Durante i movimenti di protrusione e retrusione, la mandibola non si muove esclusivamente lungo l'asse $X$, ma ruota attorno al centro dell'asse $Y$. Questo movimento condilare si manifesta anteriormente, dove l'incisivo mandibolare segue traiettorie curvilinee inverse, risultato di un complesso moto spaziale generato dalla rototraslazione sugli assi condilari. Lo spazio angolare risultante, noto come 'Spazio libero Interincisivo', è essenziale per consentire movimenti masticatori fluidi e senza ostacoli.

Questo 'Spazio libero Interincisivo' riveste un ruolo cruciale nelle funzioni masticatorie. Tuttavia, strumenti come il Sirognatograph e i sistemi elettromagnetici tradizionali trascurano la componente rotazionale dei movimenti condilari, focalizzandosi principalmente sulle traslazioni. Sebbene ciò possa essere sufficiente per alcune registrazioni, tale approccio è limitato nel cogliere la complessità dei movimenti mandibolari a sei gradi di libertà.

Cinematica Mandibolare a Sei Gradi di Libertà

Il movimento mandibolare avviene in uno spazio tridimensionale e può essere descritto come un complesso moto spaziale. Ogni condilo è associato a tre assi principali:

• Asse $Y$ (latero-mediale): Definisce la rotazione attorno all'asse cerniera trasversale ($_{t}HA$, transverse Hinge Axis).
• **Asse $Z$ (verticale):** Definisce la rotazione sull'asse cerniera verticale ($_{v}HA$).
• **Asse $X$ (antero-posteriore): Definisce la rotazione attorno all'asse cerniera orizzontale ($_{o}HA$).

A ciascun asse corrisponde un piano di riferimento anatomico:

• Piano sagittale: Mostra il tracciato condilare prodotto dal movimento di rototraslazione dell'asse trasversale ($_{t}HA$).
• Piano coronale: Associato all'asse orizzontale ($_{o}HA$).
• Piano assiale: Legato al movimento generato attorno all'asse verticale ($_{v}HA$, noto anche come asse cerniera verticale).

Va evidenziato che un piano non è generato da un asse; un asse può al massimo essere contenuto in un piano o rappresentare una direzione. Più precisamente, il movimento di un asse genera una 'superficie rigata', che descrive le traiettorie spaziali risultanti.

Asse cerniera verticale

Ci concentreremo sull’asse cerniera verticale ($_{v}HA$) per la sua rilevanza nei sistemi di registrazione cinematici come pantografi, elegnatografi e assiografi. Tuttavia, è necessario esaminare il razionale della Gnatologia Classica per comprendere l'interazione tra piani e assi nel descrivere i movimenti condilari.

• Il pantografo analogico è stato considerato un dispositivo capace di riprodurre con precisione i movimenti di confine dei tracciati condilari e di trasferirli su un articolatore completamente regolabile tramite le sue 6 piastrine.

• Successivamente, si è riportato che anche il pantografo elettronico registrava i determinanti condilari con un intervallo accettabile (argomento trattato nei capitoli successivi).

• Un determinante particolare del movimento condilare, la traslazione laterale immediata mandibolare (Movimento di Bennett), è stato oggetto di dibattito e confusione nella letteratura protesica. Tuttavia, una recente revisione della letteratura ha evidenziato una mancanza di prove sul significato clinico di questo movimento.

Nota sulla Precisione e Sugli Obiettivi dello Studio

Questo studio mira a fornire una comprensione concettuale dei principi cinematici coinvolti nella dinamica masticatoria, con un focus sulla biomeccanica mandibolare. Sebbene i calcoli siano stati eseguiti con rigore, potrebbero verificarsi discrepanze dovute a:

• Approssimazioni nei dati numerici: Differenze nei valori cartesiani legate a variabili operative.
• Limiti di rappresentazione: Uso di numeri approssimati per motivi pratici.
• Finalità cliniche: Lo scopo è descrivere concetti piuttosto che ottenere precisione assoluta.

Figura 1: Cinematica mandibolare sul piano assiale rappresentata dai markers prelevati dallo strumento ogni 20 mSec. Questi punti rappresentano i condili laterotrusivi dal punto $L_{c}$ e mediotrusivi $M_{c}$. Il Laterotrusive point (a sinistra) e il Mediotrusive point (a destra) tracciano la posizione dei condili della mandibola durante un movimento masticatorio laterale, che include movimenti complessi di traslazione e rotazione. I punti numerati ($1L_{c}$....$8L_{c}$) seguono il movimento del condilo laterotrusivo nel tempo, mentre i punti $1M_{c}$....$8M_{c}$ seguono il condilo mediotrusivo. Nell'area del Molar point e dell' Incisal point sono rappresentati i percorsi occlusali durante la masticazione.

Passi Successivi

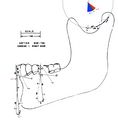
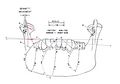
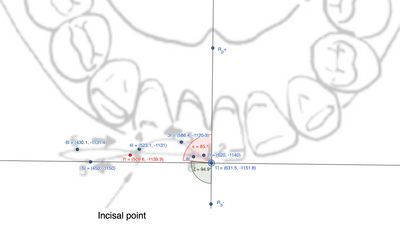
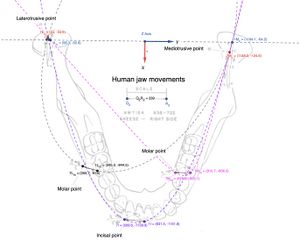
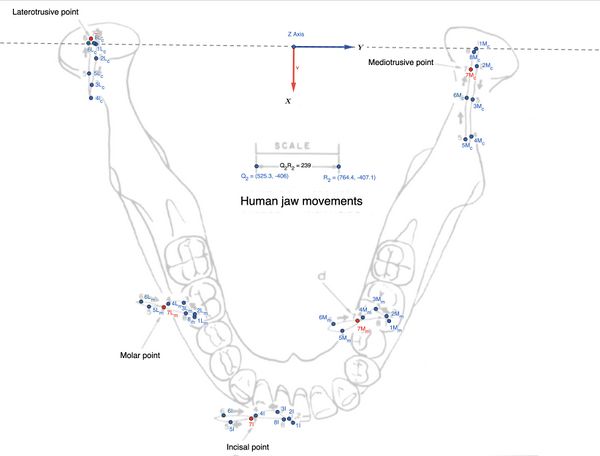
In questo capitolo, analizzeremo la cinematica dell'asse verticale ($_{v}HA$) e il fenomeno masticatorio, rappresentandolo con tracciati estratti da lavori di riferimento come quello di Lund e Gibbs.(Figura 1)

Descrizione della Calibrazione: da Pixel a Millimetri

La calibrazione di un'immagine per ottenere misurazioni accurate richiede l'attenzione a diversi fattori critici. Estrarre distanze da un'immagine può essere complesso, poiché la precisione dipende da:

1. Fattori di distorsione: Le immagini possono essere affette da distorsioni ottiche, che devono essere corrette calibrando la camera utilizzando, ad esempio, una scacchiera di riferimento.
2. Effetto prospettico: La scala di riferimento varia con la distanza dal piano di acquisizione. Per oggetti posti a diverse profondità, è necessario applicare fattori di scala specifici, calcolati utilizzando un modello come quello della pin-hole camera.
3. Distorsioni prospettiche: Queste possono essere corrette utilizzando ottiche telecentriche, particolarmente utili per applicazioni che richiedono un'elevata accuratezza, come nelle misurazioni spaziali o bioingegneristiche.

Con questa premessa, il fattore di scala utilizzato nel nostro studio rappresenta un'approssimazione valida nel contesto specifico delle immagini 2D acquisite in condizioni controllate. Tuttavia, per applicazioni più rigorose, come quelle descritte sopra, è necessario considerare strumenti e metodi avanzati per la calibrazione.

Calcolo della Distanza tra i Punti

Le coordinate dei punti sono:

$Q_{2}(525.3,-406)$ e $R_{2}(764.4,-407.1)$

La formula per la distanza euclidea è:

$d={\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}}$

Sostituendo i valori:

$d={\sqrt {(764.4-525.3)^{2}+(-407.1-(-406))^{2}}}$

$d={\sqrt {(239.1)^{2}+(-1.1)^{2}}}$

$d={\sqrt {57121.81+1.21}}={\sqrt {57123.02}}\approx 239.02\,{\text{pixel}}$

Conversione della Scala in mm

Dato che il segmento di $239.02\,{\text{pixel}}$ equivale a $1\,{\text{cm}}=10\,{\text{mm}}$, calcoliamo la conversione in mm/pixel:

${\text{Scala in mm/pixel}}={\frac {\text{Lunghezza reale (in mm)}}{\text{Distanza in pixel}}}={\frac {10}{239.02}}\approx 0.04184\,{\text{mm/pixel}}$

Quindi, ogni pixel nella figura corrisponde a circa:

$0.04184\,{\text{mm/pixel}}$.

Esempio di Applicazione: Conversione Distanza in mm

Supponiamo di voler calcolare una distanza in mm. Ad esempio, se la distanza in pixel fosse $d=100\,{\text{pixel}}$:

$d_{\text{mm}}=100\cdot 0.04184\approx 4.184\,{\text{mm}}$

Risultato Finale

La scala è:

• $239.02\,{\text{pixel/cm}}$
• $0.04184\,{\text{mm/pixel}}$

Questi valori possono essere usati per convertire qualsiasi distanza misurata in pixel nella figura in unità metriche come millimetri o centimetri.

Cinematica dei Condili

Traslazioni e Rotazioni dei Condili

Nel contesto del movimento mandibolare, i condili eseguono sia movimenti traslatori (spostamenti lineari) sia rotatori (movimenti angolari attorno a specifici assi). Questo doppio movimento, noto come rototraslazione, è fondamentale per comprendere la cinematica mandibolare.

Per descrivere la posizione e il movimento di ciascun condilo nel tempo, si utilizzano vettori di posizione, che variano in modulo e direzione a seguito del moto elicoidale. Il moto è descritto da una combinazione di spostamenti lineari e variazioni angolari che influenzano la posizione dei vettori nello spazio tridimensionale.

Vettori di Posizione del Condilo Laterotrusivo (Lavorante)

Il condilo laterotrusivo si trova sul lato in cui avviene la laterotrusione (spostamento laterale della mandibola). Durante il movimento, la sua posizione è descritta dal seguente vettore:

$P_{l}(t)=[X_{l}(t),Y_{l}(t),Z_{l}(t),\theta _{l}(t),\phi _{l}(t),\psi _{l}(t)]$

Dove:

• $X_{l}(t),Y_{l}(t),Z_{l}(t)$: Spostamenti lineari lungo gli assi cartesiani:
  • $X_{l}(t)$: Spostamento antero-posteriore.
  • $Y_{l}(t)$: Spostamento latero-mediale.
  • $Z_{l}(t)$: Spostamento verticale.

• $\theta _{l}(t)$, $\phi _{l}(t)$, $\psi _{l}(t)$: Rotazioni angolari attorno agli assi $X$, $Y$ e $Z$, descritte con gli angoli di Eulero.

Adottiamo la convenzione $X,Y,Z$, che segue l’ordine:

• $\theta _{l}(t)$: Rotazione attorno a $X$ (torsione laterale).
• $\phi _{l}(t)$: Rotazione attorno a $Y$ (apertura/chiusura).
• $\psi _{l}(t)$: Rotazione attorno a $Z$ (rotazione laterale/mediale).

Questa sequenza consente una descrizione univoca dell’orientamento del condilo nello spazio.

• 

  Figura 2: Tracciati cinematici masticatori sul piano sagittale.

• 

  Figura 2: Tracciati cinematici masticatori sul piano sagittale.

• 

  Figura 3: Tracciati cinematici masticatori sul piano coronale.

• 

  Figura 4: Tracciati cinematici masticatori sul piano assiale.

Traslazione del Condilo Mediotrusivo

Il condilo mediotrusivo, sul lato opposto al movimento laterale, si muove principalmente con una traslazione anteriore e mediale nello spazio tridimensionale. La traslazione è descritta dal seguente vettore:

$T_{M}(t)={\begin{pmatrix}X_{M}(t)\\Y_{M}(t)\\Z_{M}(t)\end{pmatrix}}$

Dove:

• $(X_{M}(t),Y_{M}(t),Z_{M}(t))$: Coordinate temporali del condilo mediotrusivo nello spazio cartesiano.

Questo tipo di traslazione influenza significativamente i tracciati occlusali, generando variazioni di orientamento durante il ciclo masticatorio.

Descrizione delle misure lineari ed angolari

Rappresentazione scalare dei tracciati condilari

Descrizione delle distanze e delle direzioni

Di seguito sono riportate le distanze calcolate tra i punti rispetto al punto di partenza (punto 1, massima intercuspidazione), considerato punto di riferimento, e le relative direzioni nello spazio, utilizzando le coordinate corrette per gli assi $X$ (antero-posteriore) e $Y$ (latero-mediale).

Calcolo delle distanze tra i punti

Le coordinate dei punti estrapolate da Geogebra dopo calibrazione, per il condilo laterotrusivo, sono:

• 1L: $(58.3,-50.9)$
• 2L: $(59,-92.3)$
• 3L: $(46.3,-169.5)$
• 4L: $(44.1,-207.7)$
• 5L: $(38.4,-136.2)$
• 6L: $(36.4,-48.2)$
• 7L: $(44,-34.9)$
• 8L: $(52.9,-48)$

Fattore di scala: $0.04184\,{\text{mm/pixel}}$

Distanze rispetto a $1L_{c}$:

$2L_{c}$:

$d={\sqrt {(59-58.3)^{2}+(-92.3-(-50.9))^{2}}}={\sqrt {(0.7)^{2}+(-41.4)^{2}}}={\sqrt {0.49+1714.36}}\approx 41.41\,{\text{pixel}}$ $d=41.41\cdot 0.04184\approx 1.734\,{\text{mm}}$

$3L_{c}$:

$d={\sqrt {(46.3-58.3)^{2}+(-169.5-(-50.9))^{2}}}={\sqrt {(-12)^{2}+(-118.6)^{2}}}={\sqrt {144+14063.96}}\approx 119.17\,{\text{pixel}}$ $d=119.17\cdot 0.04184\approx 4.99\,{\text{mm}}$

$4L_{c}$:

$d={\sqrt {(44.1-58.3)^{2}+(-207.7-(-50.9))^{2}}}={\sqrt {(-14.2)^{2}+(-156.8)^{2}}}={\sqrt {201.64+24589.44}}\approx 157.43\,{\text{pixel}}$ $d=157.43\cdot 0.04184\approx 6.59\,{\text{mm}}$

$5L_{c}$:

$d={\sqrt {(38.4-58.3)^{2}+(-136.2-(-50.9))^{2}}}={\sqrt {(-19.9)^{2}+(-85.3)^{2}}}={\sqrt {396.01+7275.09}}\approx 87.6\,{\text{pixel}}$ $d=87.6\cdot 0.04184\approx 3.66\,{\text{mm}}$

$6L_{c}$:

$d={\sqrt {(36.4-58.3)^{2}+(-48.2-(-50.9))^{2}}}={\sqrt {(-21.9)^{2}+(2.7)^{2}}}={\sqrt {479.61+7.29}}\approx 22.06\,{\text{pixel}}$ $d=22.06\cdot 0.04184\approx 0.923\,{\text{mm}}$

$7L_{c}$:

$d={\sqrt {(44-58.3)^{2}+(-34.9-(-50.9))^{2}}}={\sqrt {(-14.3)^{2}+(16)^{2}}}={\sqrt {204.49+256}}\approx 21.47\,{\text{pixel}}$ $d=21.47\cdot 0.04184\approx 0.898\,{\text{mm}}$

$8L_{c}$:

$d={\sqrt {(52.9-58.3)^{2}+(-48-(-50.9))^{2}}}={\sqrt {(-5.4)^{2}+(2.9)^{2}}}={\sqrt {29.16+8.41}}\approx 6.13\,{\text{pixel}}$

$d=6.13\cdot 0.04184\approx 0.257\,{\text{mm}}$

Rappresentazione spazio temporale dei markers

Condilo Laterotrusivo

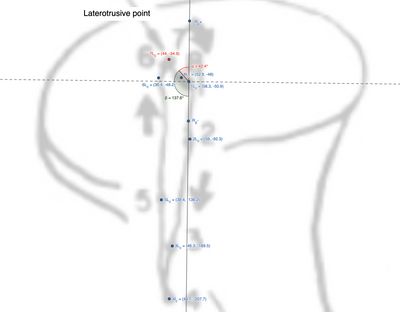
Questo paragrafo descrive il calcolo delle distanze e degli angoli tra segmenti in un piano 2D, applicati alla cinematica mandibolare. In particolare, si analizzano i movimenti articolari dei condili durante il ciclo masticatorio, rappresentati nella Figura 5 e nella Tabella 1.

Tabella 1
Tracciato masticatorio	Markers	Distanza (mm)	Direzione	Direzione $Y$
Figura 5: Markers sovrapposti in Geogebra sul tracciato del condilo laterotrusivo da modello Replicator di Lund e Gibbs.	2	1.734	Protrusiva	Parallela.
	3	4.99	Protrusiva	Lateralizzazione
	4	6.59	Protrusiva	Lateralizzazione
	5	3.66	Inversione	Inversione
	6	0.923	Retrusiva	Lateralizzazione
	7*	0.898	Protrusiva	Medializzazione
	8	0.257	Protrusiva	Medializzazione

Dalla figura e dalla tabella emerge che il punto $7L_{c}$ rappresenta l'inversione del moto condilare, con il passaggio verso un percorso mediale diretto alla massima intercuspidazione. La distanza tra il punto $7L_{c}$ e $1L_{c}$, pari a circa $0.898\,{\text{mm}}$, definisce il movimento di Bennett.

La direzione angolare è stata calcolata come: $\theta =131.87^{\circ }$ e $\theta '=42^{\circ }$.

Per approfondire, il calcolo dettagliato è riportato di seguito:  Calcolo dettagliato: distanza tra $P_{1}=(58.3,-50.9)$ e $P_{7}=(44,-34.9)$, distanza euclidea ${\sqrt {(-14.3)^{2}+(16)^{2}}}\approx 21.47\,{\text{pixel}}$, convertita in mm come $21.47\times 0.04184\approx 0.898\,{\text{mm}}$, angolo $\theta =\arccos(-0.6665)\approx 131.87^{\circ }$.

Molare Laterotrusivo

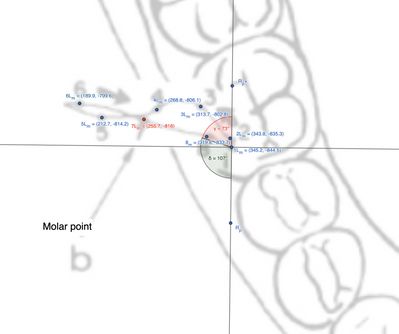
Questo paragrafo analizza i movimenti articolari del molare ipsilaterale al condilo laterotrusivo, basandosi sul calcolo delle distanze tra punti e degli angoli tra vettori mediante trigonometria vettoriale (Figura 6 e Tabella 2).

Tabella 2
Tracciato masticatorio	Markers	Distanza (mm)	Direzione $X$	Direzione dinamica $Y$
Figura 6: Marker grafici rilevati dal 'Replicator' durante la masticazione sul lato destro	2	0.39	Indietro	Lateralizzazione
	3	2.18	Indietro	Lateralizzazione
	4	3.57	Indietro	Lateralizzazione
	5	5.68	Indietro	Lateralizzazione
	6	6.76	Indietro	Inversione
	7*	3.93	Indietro	Medializzazione
	8	1.15	Indietro	Medializzazione

Osservando la figura e la tabella, si evidenziano le distanze e le direzioni dei punti marcati. In particolare, la distanza tra il punto $7L_{m}$ e il punto iniziale $1L_{m}$ è stata calcolata come circa $3.93\,_{\text{mm}}$, con un angolo tra i vettori pari a $73^{\circ }$. Calcolo dettagliato: 1. Definizione dei vettori: ${\vec {AB}}=7L_{m}-1L_{m}=(255.7,-816.0)-(345.2,-844.5)=(-89.5,28.5)$ ${\vec {AC}}=R_{p}-1L_{m}=(346.6,-727.1)-(345.2,-844.5)=(1.4,117.4)$ 2. Magnitudine dei vettori: $|{\vec {AB}}|={\sqrt {(-89.5)^{2}+(28.5)^{2}}}\approx 93.93$ $|{\vec {AC}}|={\sqrt {(1.4)^{2}+(117.4)^{2}}}\approx 117.41$ 3. Prodotto scalare: ${\vec {AB}}\cdot {\vec {AC}}=(-89.5)(1.4)+(28.5)(117.4)=2928.4$ 4. Calcolo dell'angolo: $\cos(\theta )={\frac {{\vec {AB}}\cdot {\vec {AC}}}{|{\vec {AB}}|\cdot |{\vec {AC}}|}}={\frac {2928.4}{93.93\cdot 117.41}}\approx 0.292$ $\theta =\arccos(0.292)\approx 73.02^{\circ }$

Area Incisale

Questo paragrafo analizza i movimenti articolari dell’incisivo sul lato lavorante. Utilizzando le coordinate dei punti $1_{I}$, $7_{I}$ e $R_{p}^{+}$ in uno spazio 2D, sono calcolate le distanze lineari e l’angolo tra i segmenti che collegano questi punti.(Figura 7, tabella 3)

Tabella 3
Tracciato masticatorio	Markers	Distanza (mm)	Direzione $X$	Direzione dinamica $Y$
Figura 7: Markers grafici rilevati dal 'Replicator' durante la masticazione nell'area incisale sul lato destro.	2	0.69	Retrusiva	Lateralizzazione
	3	2.30	Retrusiva	Lateralizzazione
	4	4.61	Retrusiva	Lateralizzazione
	5	7.58	Protrusiva	Lateralizzazione
	6	8.54	Retrusiva	Inversione
	7*	5.12	Retrusiva	Medializzazione
	8	1.75	Retrusiva	Medializzazione

Per i tracciati dell’area incisale, la distanza tra i punti $1_{I}$ e $7_{I}$ è di $5.12\,{\text{mm}}$, con un angolo calcolato approssimativamente pari a $85.1^{\circ }$.

Per approfondire i calcoli, ecco la spiegazione dettagliata Calcolo dettagliato: Coordinate dei punti: $1_{I}=(631.5,-1151.8)$, $7_{I}=(509.6,-1139.9)$, $R_{p}^{+}=(634.3,-912.8)$. Vettori: ${\vec {1I7I}}=(-121.9,11.9)$, ${\vec {1IR_{p}^{+}}}=(2.8,239)$. Norme: $|{\vec {1I7I}}|={\sqrt {(-121.9)^{2}+(11.9)^{2}}}\approx 122.49$, $|{\vec {1IR_{p}^{+}}}|={\sqrt {(2.8)^{2}+(239)^{2}}}\approx 238.95$. Prodotto scalare: ${\vec {1I7I}}\cdot {\vec {1IR_{p}^{+}}}=(-121.9)(2.8)+(11.9)(239)\approx 2502.78$. Coseno dell’angolo: $\cos(\theta )={\frac {{\vec {1I7I}}\cdot {\vec {1IR_{p}^{+}}}}{|{\vec {1I7I}}|\cdot |{\vec {1IR_{p}^{+}}}|}}={\frac {2502.78}{122.49\cdot 238.95}}\approx 0.0855$. Angolo: $\theta =\arccos(0.0855)\approx 85.1^{\circ }$.

Molare mediotrusivo

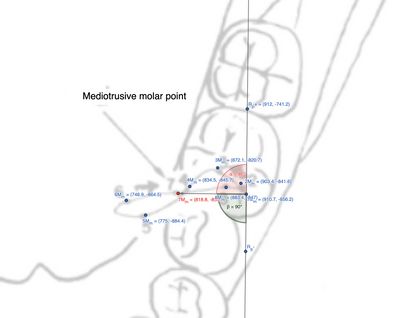
L’analisi del moto cinematico mandibolare nel molare mediotrusivo evidenzia un progressivo aumento dell’angolo di direzione rispetto al molare laterotrusivo ($73^{\circ }$) e all’incisivo ($85^{\circ }$), fino al massimo valore rilevato nel condilo ($180^{\circ }$). Questo angolo, noto come angolo di svincolo mediotrusivo, si forma tra la cuspide centrale e quella distale del primo molare. La Tabella 4 e la figura 8 mostrano le distanze tra i punti del tracciato e il punto $1M_{m}$.

Tabella 4
Tracciato mediotrusivo molare	Markers	Distanza (mm)	Direzione $X$	Direzione dinamica $Y$
Figura 8: Markers rilevati dal 'Replicator' durante la masticazione sul lato destro.	2	0.68	Retrusiva	Medializzazione
	3	2.19	Retrusiva	Medializzazione
	4	3.22	Retrusiva	Medializzazione
	5	5.79	Protrusiva	Medializzazione
	6	7.22	Protrusiva	Inversione
	7*	4.81	Retrusiva	Lateralizzazione
	8	1.18	Retrusiva	Lateralizzazione

La distanza lineare tra il punto $1M_{m}$ e $7M_{m}$ è stata calcolata come $4.81\,{\text{mm}}$, con un angolo approssimativo di $\theta =91.33^{\circ }$. Calcolo dettagliato: Vettori: ${\vec {1M_{m}7M_{m}}}=(818.8-910.7,-855.1-(-856.2))=(-91.9,1.1)$ ${\vec {1M_{m}R_{p}^{+}}}=(912-910.7,-741.2-(-856.2))=(1.3,115)$. Norme: $|{\vec {1M_{m}7M_{m}}}|={\sqrt {(-91.9)^{2}+(1.1)^{2}}}\approx 91.92$, $|{\vec {1M_{m}R_{p}^{+}}}|={\sqrt {(1.3)^{2}+(115)^{2}}}\approx 115.02$. Prodotto scalare: ${\vec {1M_{m}7M_{m}}}\cdot {\vec {1M_{m}R_{p}^{+}}}=(-91.9\cdot 1.3)+(1.1\cdot 115)=-119.47+126.5=7.03$. Coseno: $\cos(\theta )={\frac {7.03}{91.92\cdot 115.02}}\approx 0.000665$. Angolo: $\theta =\arccos(0.000665)\approx 90^{\circ }$.

Condilo Mediotrusivo

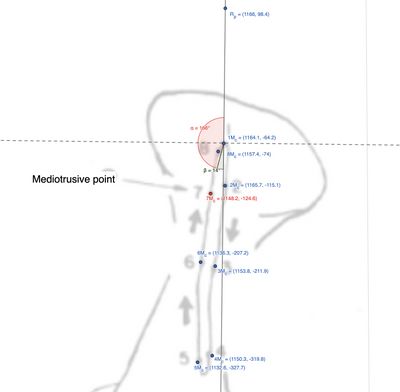
Il calcolo dell’angolo tra i segmenti $1M_{c}-7M_{c}$ e $1M_{c}-R_{p}^{c}$ è fondamentale per analizzare i movimenti articolari nel sistema masticatorio. Questa analisi consente di comprendere come si muovono i segmenti articolari rispetto a un punto di riferimento. ( Figura 9, tabella 5)

Tabella 5
Tracciato masticatorio	Markers	Distanza (mm)	Direzione $X$	Direzione $Y$
Figura 9: Markers rilevati dal 'Replicator' durante la masticazione sul lato destro nell'area incisale.	2	2.13	Protrusiva	Medializzazione
	3	6.19	Protrusiva	Medializzazione
	4	10.70	Protrusiva	Medializzazione
	5	11.09	Protrusiva	Inversione
	6	6.09	Protrusiva	Lateralizzazione
	7*	2.61	Protrusiva	Lateralizzazione
	8	0.50	Protrusiva	Lateralizzazione

La distanza tra il punto $1M_{c}$ e $7M_{c}$ è risultata $6.88\,{\text{mm}}$, con un angolo calcolato di $\theta =166^{\circ }$. Sottraendo da $180^{\circ }$, si ottiene un angolo di $14^{\circ }$, noto come Angolo di Bennett. Per il calcolo dettagliato Calcolo sintetico: Vettore: ${\vec {AB}}=(-15.9,-60.4)$, ${\vec {AC}}=(0.2,52.5)$. Prodotto scalare: ${\vec {AB}}\cdot {\vec {AC}}=-3172.62$. Norme: $|{\vec {AB}}|=62.93$, $|{\vec {AC}}|=52.50$. $\cos(\theta )={\frac {-3172.62}{62.93\cdot 52.50}}\approx -0.971$, $\theta =\arccos(-0.971)\approx 166^{\circ }$.

Discussione sulla rototraslazione condilare

Il moto rototraslazionale dei condili è cruciale per comprendere la cinematica mandibolare. Se i condili ruotassero attorno a un punto fisso, i tracciati dei molari e degli incisivi sarebbero semplici archi di cerchio. Tuttavia, i movimenti reali includono sia rotazione che traslazione.

Durante la laterotrusione, il condilo ipsilaterale combina rotazione attorno all’asse verticale e traslazione laterale, mentre il condilo mediotrusivo si muove principalmente in direzione mediale e anteriore, generando il "Tragitto orbitante".

Descrizione matematica

La rototraslazione del condilo laterotrusivo può essere rappresentata come:

$x_{m}=x_{m0}\cos(\theta )-y_{m0}\sin(\theta )+T_{x}$ $y_{m}=x_{m0}\sin(\theta )+y_{m0}\cos(\theta )$

Dove:

• $(x_{m0},y_{m0})$: posizione iniziale del molare ipsilaterale.
• $T_{x}$: traslazione laterale lungo l’asse $x$.
• $(x_{m},y_{m})$: posizione finale.

Figura 10a: Rappresentazione di una conica.

Man mano che il condilo si muove, le coordinate $(x_{m},y_{m})$ descrivono una traiettoria ellittica proiettata su un piano 2D. Questo avviene perché il centro di rotazione istantaneo del condilo non è fisso ma si sposta continuamente.

Un fenomeno simile si osserva per il condilo mediotrusivo e gli incisivi, le cui traiettorie sono influenzate da traslazioni mediali e anteriori e da rotazioni attorno all’asse verticale. Questi tracciati non sono ellissi perfette, ma curve più complesse a causa delle variazioni nei movimenti condilari.

I tracciati dentali sono correlati ai movimenti dei condili e offrono preziose informazioni sulla cinematica mandibolare, per cui sarebbe auspicabile spendere qualche parola in più sulla velocità del moto masticatorio e la rappresentazione di questa cinematica mandibolare in un forma geometrico/matematica chiamata 'Conica'.

Rappresentazione in una 'Conica'

Un modello basato su una conica passante per cinque punti strategici aiuta a rappresentare meglio queste traiettorie, come illustrato nella figura 10a.

In sintesi, i tracciati dei molari e degli incisivi assumono forme ellittiche complesse, poiché il centro di rotazione condilare si sposta continuamente. Questo modello aiuta a comprendere meglio la complessità dei movimenti mandibolari. La rappresentazione spaziale dei markers etichettati come punto 1,2,3.....8 ci ha restituito distanze in millimetri ed angoli tra i punti ed il punto 1 (massima intercuspidazione) considerato come riferimento. Rimane ora da razionalizzare il contenuto geometrico matematico estrapolandone il concetto di velocità nelle diverse aree del sistema ( condili e punti occlusali) e la rappresentazione del fenomeno cinematico attraverso un formalismo matematico denominato 'conica'. Solo dopo formalizzato questo argomento si potranno generare delle asserzioni sul tema specifico.

Analisi delle Velocità nella cinematica masticatoria

Velocità Lineari e Angolari

Il movimento mandibolare rappresenta una combinazione complessa di traslazioni lineari e rotazioni angolari. Questi due fenomeni possono essere descritti matematicamente come segue:

• Velocità Lineare: È la variazione della posizione di un punto nello spazio rispetto al tempo. Per un punto $P(t)$ con coordinate $(x(t),y(t),z(t))$, la velocità lineare è definita come: $v={\sqrt {\left({\frac {dx}{dt}}\right)^{2}+\left({\frac {dy}{dt}}\right)^{2}+\left({\frac {dz}{dt}}\right)^{2}}}$. La velocità lineare è particolarmente significativa nei movimenti traslatori, come quelli del condilo mediotrusivo, che si sposta lungo traiettorie più lunghe piuttosto che il fenomemo rototraslatorio dal punto $1L_{c}-8L_{c}$ del condilo laterotrusivo.
• Velocità Angolare: È la variazione dell’angolo di rotazione attorno a un asse rispetto al tempo. Considerando un angolo $\theta (t)$, la velocità angolare è definita come: $\omega ={\frac {d\theta }{dt}}$. Questa componente predomina nei movimenti di rotazione del condilo laterotrusivo dove l’arco descritto dalla rotazione è più rilevante rispetto alla traslazione.

Relazione Geometrica tra Velocità Lineare e Angolare

Se un punto si muove lungo un arco di raggio $r$, le velocità lineare $v$ e angolare $\omega$ sono legate dalla relazione:

$v=r\cdot \omega$.

In ambito mandibolare:

Il condilo laterotrusivo, con un raggio $r$ più piccolo, sviluppa una velocità angolare $\omega$ maggiore.

Il condilo mediotrusivo, con un raggio maggiore, mostra una velocità lineare $v$ più elevata per sincronizzarsi con il condilo laterotrusivo.

Utilizzando i dati relativi a distanze e angoli riportati in tabelle 1,2,3,4 e 5 e nello specifico, per semplificazione soltanto la distanza tra il punto$1-7$ abbiamo che sul Condilo Laterotrusivo $L_{c}$ la distanza percorsa è di $d_{L_{c}}=0.898\,{\text{mm}}$ con un angolo formato tra i punti occlusali $1-7$ con vertice in $1L_{c}$ calcolato in $\approxeq \theta _{L_{c}}''=5^{\circ }$ per distinguerlo da $\theta _{L_{c}}=42^{\circ }$ e che rimane simile per tutti le aree del sistema ( condilo mediotrusivo, molari ed incisivo). Il moto è prevalentemente rotatorio, con una componente traslatoria ridotta.

La tabella X riassume i parametri per la valitazione analitica delle velocità:

Nel Condilo Mediotrusivo (M_c), invece, la distanza percorsa è $d_{M_{c}}=2.61\,{\text{mm}}$. Il movimento è prevalentemente traslatorio, suggerendo una velocità lineare più elevata.

---

Analisi del Movimento Simultaneo verso il Punto 1

L'analisi del movimento simultaneo durante la chiusura mandibolare è cruciale per comprendere la sincronizzazione tra le diverse strutture coinvolte. Ogni elemento della mandibola (condili, molari e incisivi) segue un proprio percorso, percorrendo distanze differenti, ma tutti devono 'ritornare contemporaneamente alla posizione di massima intercuspidazione (punto 1). Poiché le distanze percorse sono diverse, la velocità di ciascun segmento deve variare in modo proporzionale per garantire il 'tempo di ritorno uniforme'.

Sincronizzazione Temporale e Differenze nelle Distanze

Principio della sincronizzazione: Indipendentemente dalla distanza percorsa, 'tutti i punti devono raggiungere il punto 1 nello stesso tempo' $t_{tot}$.

Distanze percorse dai vari segmenti:

Tabella X: Distanze percorse dai marker

Struttura	Distanza percorsa $d$ (mm)
Condilo laterotrusivo $L_{c}$	$0.898$
Condilo mediotrusivo $M_{c}$	$2.61$
Molare laterotrusivo $L_{m}$	$3.93$
Molare mediotrusivo $M_{m}$	$4.81$
Incisivo $I$	$5.12$

Poiché i valori di $d$ sono diversi, ciascuna struttura deve adattare la sua 'velocità di ritorno' per rispettare $t_{tot}$.

---

Calcolo della Velocità di Ritorno

Assumiamo che il tempo totale $t_{tot}$ sia governato dal condilo laterotrusivo $L_{c}$, il cui valore sperimentale è:

$t_{tot}={\frac {d_{L_{c}}}{v_{L_{c}}}}={\frac {0.898}{224.5}}\approx 0.004{\text{ s}}$

Dove $v_{L_{c}}=224.5$ mm/s è il valore medio calcolato sulla base della letteratura ($222-225$ mm/s).

Ora possiamo calcolare le velocità per ogni segmento usando la formula:

$v={\frac {d}{t_{tot}}}$

Velocità di ritorno per ogni segmento:

Velocità calcolate per i vari settori

Struttura	Distanza $d$ (mm)	Velocità $v$ (mm/s)	Velocità $v$ (m/s)
Condilo laterotrusivo $L_{c}$	$0.898$	$224.5$	$0.2245$
Condilo mediotrusivo $M_{c}$	$2.61$	$652.5$	$0.6525$
Molare laterotrusivo $L_{m}$	$3.93$	$982.5$	$0.9825$
Molare mediotrusivo $M_{m}$	$4.81$	$1202.5$	$1.2025$
Incisivo $I$	$5.12$	$1280.0$	$1.2800$

Osservazioni:

✔️ La velocità **aumenta** con la distanza percorsa.

✔️ L’incisivo ha la velocità più alta perché percorre il tragitto più lungo.

✔️ Il condilo laterotrusivo ha la velocità più bassa perché si muove prevalentemente in **rotazione**.

---

Interpretazione Biomeccanica

🔹 Ruolo del Condilo Laterotrusivo $L_{c}$

La velocità relativamente bassa ($0.2245\,{\text{m/s}}$) e la breve distanza percorsa ($0.898\,{\text{mm}}$) riflettono un movimento prevalentemente rotatorio. Il $L_{c}$ funge da "pivot" durante il movimento mandibolare. Movimento prevalentemente 'rotatorio' attorno a un asse verticale. Breve distanza percorsa 'velocità minore'. Funziona come 'fulcro' del movimento mandibolare. Questo termine 'Fulcro' riprende l'asserzione precedentemente esposta di come il fulcro in questo caso dell'asse cerniera verticale assuma un posto di primo piano nel fenomeno cinematico mandibolare.

🔹 Ruolo del Condilo Mediotrusivo $M_{c}$

Con una velocità media di $0.6525\,{\text{m/s}}$, il $M_{c}$ compensa la distanza maggiore ($2.61\,{\text{mm}}$) con una componente traslatoria predominante. Questo condilo stabilizza il movimento mandibolare e bilancia la forza generata dal $L_{c}$. Movimento prevalentemente 'traslatorio' lungo una traiettoria più ampia. Distanza maggiore 'velocità superiore'. Stabilizza il movimento per sincronizzarsi con il condilo laterotrusivo. Se questo condilo è stabilizzatore avrà un significato particolare nel sincronizzarsi con il condilo laterotrusivo e ciò anticipa l'interessante argomento del prossimo capitolo che riguarda la 'magia della sfera condilare'.

🔹 Ruolo dei Molari

Il molare laterotrusivo ($L_{m}$) mostra una velocità più elevata ($0.9825\,{\text{m/s}}$) rispetto al condilo $L_{c}$, suggerendo che la sua traiettoria dipenda sia dalla rotazione del $L_{c}$ sia dalla traslazione del $M_{c}$. - Il molare mediotrusivo ($M_{m}$) ha una velocità simile ($1.2025\,{\text{m/s}}$) all’incisivo, suggerendo un maggiore coinvolgimento nei movimenti traslatori. Il 'molare laterotrusivo' ($L_{m}$) segue una traiettoria influenzata sia dalla 'rotazione' del condilo laterotrusivo sia dalla 'traslazione' del condilo mediotrusivo. Il 'molare mediotrusivo ($M_{m}$) ha un movimento più 'traslatorio', con velocità più elevata rispetto a $L_{m}$.

🔹 Ruolo dell’Incisivo

La velocità massima ($1.28\,{\text{m/s}}$) riflette il suo ruolo come punto guida dei movimenti mandibolari. L’incisivo integra i contributi biomeccanici dei due condili, mostrando una traiettoria influenzata sia dalla rotazione che dalla traslazione. Percorre la distanza più lunga, quindi 'raggiunge la massima velocità'. La sua traiettoria è influenzata sia dalla rotazione del condilo laterotrusivo che dalla traslazione del condilo mediotrusivo.

📌 In conclusione, la mandibola bilancia le 'differenze di distanza' attraverso variazioni di velocità, garantendo che tutti i punti raggiungano 'contemporaneamente' la massima intercuspidazione. Implicazioni: Questo modello può essere utilizzato per comprendere le 'disfunzioni temporomandibolari (DTM)'. L'analisi cinematica è fondamentale per lo sviluppo di 'protesi occlusali ottimizzate' ed evitare incongruenze ed interferenze occlusali.

Future ricerche possono affinare la modellizzazione basata sulle 'coniche e sugli schemi neurofisiologici' associati al movimento mandibolare.

---

---

Bibliography & references