Logic of medical language: Introduction to quantum-like probability in the masticatory system

Go to top

Logic of medical language: Introduction to quantum-like probability in the masticatory system

Article by Gianni Frisardi · Alice Bisirri · Flavio Frisardi

Abstract: This study addresses the epistemological foundations of the concept of 'Malocclusion,' proposing a neurophysiological reinterpretation that challenges the traditional orthodontic perspective. Through the analysis of clinical cases, the limits of classical macroscopic observation in diagnosing malocclusion are highlighted, introducing a quantum interpretation that considers the superposition of system states. Specifically, Schrödinger’s paradox is explored as a metaphor to describe how a complex system, like the masticatory system, can exist in a mixed state, which cannot be reduced to a simple dichotomy of healthy versus sick.

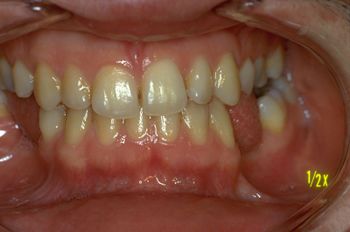
The clinical example of a patient who underwent orthognathic surgery (Figure 2) demonstrates how an apparently "normal" occlusal condition can conceal severe trigeminal system anomalies, revealed only through advanced electrophysiological tests. Conversely, a patient with clear signs of malocclusion (Figure 1) might present a more balanced neurophysiological profile. These findings suggest that macroscopic observable reality may not fully reflect the deeper state of the system.

By applying principles of quantum physics, such as the superposition of states and wave function collapse, we argue that classical clinical observation is insufficient to grasp the complexity of the masticatory system. Only through the integration of advanced diagnostic techniques, like trigeminal motor evoked potentials (Root-MEPs) and other neurophysiological methods, can diagnostic uncertainty be reduced, enhancing the ability to detect underlying dysfunctions early on.

The study calls for a reconsideration of the concept of 'Normocclusion' and a reassessment of current diagnostic models, proposing an interdisciplinary approach that bridges neurophysiology and dentistry. This work paves the way for a new understanding of the masticatory system, moving beyond rigid statistical classification and embracing a more dynamic and complex view of dental and neurological health.

Introduction

For the second time we find ourselves faced with an epistemological study of a topic on which most of the dental rehabilitation disciplines are based, that of 'Malocclusion' which in the light of what has been said in the previous chapters deserves clarification.

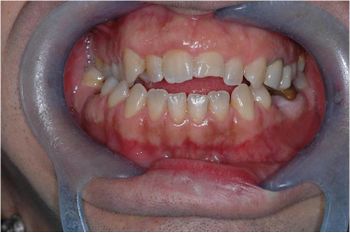
In the first chapter 'Introduction' we have already mentioned the patient in figure 1 in which it would be irreverent towards the orthodontics discipline not to consider a state of 'Malocclusion' but in some way we have also questioned the 'Axiomatic Information' by replacing the classic orthodontic dogma with a neurophysiological vision of the system status of the patient. From this approach it was clear that mesoscopic reality is very different from macroscopic reality to which, we are used to.

But if this is an anomaly, then, what should we expect from the patient in figure 2 undergoing orthognathic surgery (read descriptive caption) ?

Figura 1: Patient n ° 1 with open bite and right posterior crossbite which in orthodontic terms is considered 'Malocclusion'.
Figura 1: Patient n ° 2 after orthognathic surgery therapy for a III skeletal class. The restoration of 'Normal occlusion' is formally optimal, at least, with respect to the occlusal image of patient n°1. Apart from a slight deviation of the incisal central line and the partial mandibular edentulism, the patient reports a remarkable aesthetic satisfaction and good apparent masticatory function with great satisfaction of the maxillofacial surgeons.

The patient treated with orthognathic surgery (Fig.2) subjected to trigeminal electrophysiological examinations returned an extremely severe 'System state' picture with marked asymmetries of trigeminal reflexes so as to induce a neurophysiopathological study. This data points to a 'Malocclusion' even if the intermaxillary relationships objectively appear in a much more congruent condition occlusally than that of patient n ° 1 in figure 1.

Having said this, it makes us think:

'Can the profound reality of a 'System state' be reduced only to a macroscopic observation (Observable) if such 'Complex system' is a set of mixed states? Furthermore, the sharing of an interpretation of "Normocclusion or Malocclusion" through a classical statistical description has nothing to do with a quantum interpretation of reality because in the classical we observe macroscopic phenomena (mandibular movements, TMJ, etc.) while in reality quantum we are dealing with mesoscopic phenomena such as synaptic transmissions.

Here comes a very extravagant and risky but contextually significant argument, what in quantum physics is called superposition of states in a 'System'.

«I am perplexed about what has been said because at this point I no longer have those axiomatic certainties of the past .... give me a concrete example to understand where you want to go.»
(Of course, I will immediately satisfy you by explaining the paradox of Schrödinger's cat)

Schrödinger's cat

The "philosophy" of the superposition of quantum states

Figura 3: The structure of the experimental apparatus. Apparently, the cat can be both alive and dead at the same time.

Nel 1935 Erwin Schrödinger^[1]^[2]: in order to highlight the paradoxical results of the Copenhagen interpretation he proposed an imaginary experiment in which a cat is placed in a box containing a vial sealed with poison. Thanks to a well-constructed mechanism, the vial could break. Figure 3 graphically represents the imaginary device just exposed. To better understand the meaning of this reference to quantum, we report a specific content extracted from Wikipedia.^[3]

A cat is locked up in a steel box together with the following infernal machine (which must be protected from the possibility of being grabbed directly by the cat): in a Geiger counter there is a tiny portion of radioactive substance, so little that in the course of a now perhaps one of its atoms will disintegrate, but also, equally likely, none; if the event occurs, the counter signals it and activates a relay of a hammer which breaks a vial with cyanide. After leaving this whole system undisturbed for an hour, it would appear that the cat is still alive if in the meantime no atom had disintegrated, while the first atomic disintegration would have poisoned it.

The mathematic function $\psi$ of the whole system leads to the affirmation that in it the live cat and the dead cat are not pure states, but mixed with equal weight.^[4]»

«mixed with equal weight, since the patient's events can only be two, healthy or sick, means 50%»
(I'm curious to know where you want to go)

Often the result of the experiment is presented in the following terms. After an interval equal to the half-life, the atom may or may not have decayed with the same probability, so it is in a superposition of the two states: in Dirac notation, the state of the atom is:

$|A\rangle ={\frac {1}{\sqrt {2}}}\,\left(|{\textrm {lapsed}}\rangle +|{\textrm {non}}\;{\textrm {lapsed}}\rangle \right)$

We begin to employ notions of quantum mathematics, in fact, the acronym $|A\rangle$ stands for 'ket'^[5]

But since the decay determines the fate of the cat, it should be considered both alive and dead:

$|G\rangle ={\frac {1}{\sqrt {2}}}\,\left(|{\textrm {dead}}\rangle +|{\textrm {live}}\rangle \right)$

at least until a direct observation is carried out by opening the box. Here it should be remembered that direct observation consists of an observer and a means of measurement.

The apparent paradox arises from the fact that in quantum mechanics it is not possible to classically describe objects, and a probabilistic representation is used: to show the fact that a particle can be placed in different positions, for example, it is described as if it were simultaneously in all the positions it can take. To every possible position corresponds the probability that observing the particle it is in that position. The observation operation, however, irremediably modifies the system since once observed in a position the particle definitively assumes that position (ie it has probability 1 of being there) and therefore it is no longer in a "superposition of states".

Returning to the case of the cat, however, it should be noted that the above description is incorrect^[6]. The same conclusion of Schrödinger, who nevertheless never uses the term "paradox", is expressed in very different terms: Schrödinger refers to the wave function of the whole system , not to that of the cat. In fact, quantum theory states that the atom + cat system is described by the quantum correlation state.

$|A,G\rangle ={\frac {1}{\sqrt {2}}}\,\left(|{\textrm {atom}}\;{\textrm {lapsed,}}\;{\textrm {cat}}\;{\textrm {dead}}\rangle +|{\textrm {atom}}\;{\textrm {non}}\;{\textrm {lapsed,}}\;{\textrm {cat}}\;{\textrm {live}}\rangle \right).$

It is therefore not correct to say that the cat is in a superposition of two states, because the superposition affects the entire system ^[7]. The fundamental difference is that the two subsystems, i.e. the atom and the cat taken individually, are rather described by a statistical mixture ^[8]. The uncertainty about the fate of the cat is "classic": it is alive or dead with a probability of 50%, without any interference between the two different states.

The perplexity expressed by Schrödinger lies in the fact that quantum mechanics is apparently also applicable to a living being, which can find itself in a state of quantum correlation ( entanglement ) with a particle. It is therefore legitimate to ask whether even a macroscopic object should obey the laws of quantum mechanics, without the possibility of verifying its effects at an experimental level.

Schrödinger described the previously described diabolical device whereby a feline would become entangled with a single atom. The system would be described by a wave function, commonly abbreviated with $\psi$ , which represents, at the same time, the live cat with the excited atom and the dead cat with the atom returned to the state fundamental, after its decay triggered the lethal device. Quantum physics experts will object that the cat is an open complex system, which cannot, even at the start of the cruel experiment, be described by a $\psi$ wave function. The reasoning, however, raises an important question: Why, and how, does the weirdness of the quantum world disappear in macroscopic systems?^[9]

The peculiarity is that the breaking of the vial is determined by the decay of particles (process subject to quantum rules). Quantum rules (microscopic particles) are very different from those of macroscopic physics: with this thought experiment, however, it was possible to have the cat's life conditioned by quantum rules.

It is interesting to see how Schrödinger managed to create with an imaginary experiment to involve the consequences of quantum theory to the macrospic world represented by the cat.

The mathematical formalism

The cat experiment is connected, as mentioned, to the problem of measurement. A quantum system is in a superposition of two states $A$ and $B$ (mathematically represented by the 'ket' $|A\rangle +|B\rangle$ ); an observation of it forces the system to go definitively or in the $|A\rangle$ or in the $|B\rangle$ . The presence of the cat causes the superposition in which the atom is found to be "transferred" to the overall system (atom + cat). The atom, therefore, is no longer in a superposition, just as the cat is not.From this first presentation we understand the meaning of the argument

The only way to understand the condition of the cat remains to open the box and check if the cyanide ampoule is broken and consequently the cat is dead.

The formula representing this situation is the following:

$\psi (t_{0})=|1\rangle |live\rangle$ which can be read in the following way: the wave function $\psi$ over time $t_{0}$ is the same as ket $|1\rangle$ and the cat is alive

A state that will then evolve in a time period $T$ in which (except for phase and normalization factors) the two states in $t_{1}$ , (due to the observer's ignorance?) , coexist:

$\psi (t_{1})=|1\rangle |live\rangle +|0\rangle |dead\rangle$

What will collapse state $\psi (t_{1})=|1\rangle |live\rangle +|0\rangle |dead\rangle$ into one $|1\rangle |live\rangle$ or only $|0\rangle |dead\rangle$ ?

Leaving aside the various interpretations, for orthodox thought the collapse will be caused by the interaction with a macroscopic measuring object, that is when this 'Observable' is observed by the observer. We have therefore generated a (observable) System comprising the physical State of the System itself, an observer and a measuring instrument.

To be precise, the formula $\psi (t_{1})=|1\rangle |live\rangle +|0\rangle |dead\rangle$ is incomplete, you need to multiply each term to the right of the equation with a number. The number indicates the 'probability' that the specific event will occur, the complete formula will be:

$\psi (t_{1})={\sqrt {p_{1}}}|1\rangle |live\rangle +{\sqrt {p_{0}}}|0\rangle |dead\rangle$

The number indicates the probability (square rooted) that the specific event will occur.

Let's take an example that brings us back to the medical field:

if the $|1\rangle |healthy\rangle$ event has a 50% chance of occurring and the $|0\rangle |sick\rangle$ event has 50% to occur then the formula becomes (unless phase factors)

$\psi (t)={\sqrt {5}}0\%|1\rangle |healthy\rangle +{\sqrt {5}}0\%|0\rangle |sick\rangle$

which in more exact terms mathematically turns into

$\psi (t)={\sqrt {0}}.5|1\rangle |healthy\rangle +{\sqrt {0}}.5|0\rangle |sick\rangle$

«Please give me an example otherwise I won't follow you»
(yes of course it's simpler than you think)

Let's imagine that an 'Observable' is the human brain that from a purely symbolic point of view could represent Schrödinger's cat box, given that the skull contains an organ of such excellent functionality.

At this point, in the absence of particular symptoms and clinical signs, we can say that the subject is healthy. In practice we have done nothing but say the same thing that can be said about Schrödinger's cat box and that is that 50% of the cat is alive (healthy subject) and 50% could be dead (sick subject).

Take into account the subtlety of Schrödinger's metaphor because most people belittle the concept by reducing everything to a naive logic in which the cat was already dead even before opening the box and my 6-year-old nephew would have reached this point too.Schrödinger's real metaphorical sense does not refer directly to the cat (macroscopic structure) but to the uranium atom (microscopic structure) which decays (dead cat) with a random temporal probability implying that the cat's life is linked to the temporal random probability of the decay of uranium. In short, the interpretation that derives from the macroscopic observable would be a selective filter that delays the interpretation of the microscopic observable, which means that the absence of symptoms could be a phenomenon dampened by the macromolecular filter.

In this sense, from the moment in which the uranium, following its own random decay process, activates the hammer that breaks the ampoule and the cyanide spreads into the box. The time elapsing from the decay to the actual death of the cat $\Delta (t)$ corresponds to the superposition of states.

We will often return to these topics during the readings, especially in describing the various clinical cases that will be reported, denoting the temporal differences between normal clinical situations and manifestation of symptoms,

This $\Delta (t)$ is the superposition of states and the collapse of the wave function (dead or alive cat) corresponds to a mainly quantum dialectic.

Returning to our example, to understand if the subject actually, even better the subject's brain is intact or unstructured (the term healthy or sick is still a further step) we should open the box and see inside the state of the Central Nervous System.

Not even Schrödinger would have used this metaphor so we invented measuring instruments .... fantastic !!!

«but what do they measure ....»
(it is not so much what it measures but how the measure is interpreted)

Figure 4: An EEG trace corresponds to the space-time summation of a series of wave frequencies

(\delta ,\theta ,\alpha ,\beta ,\gamma )

where a dot (red / arrow) will correspond to positions spatially different than the recorded wave frequencies. (Lagrange coordinates)

Electroencephalography (EEG)

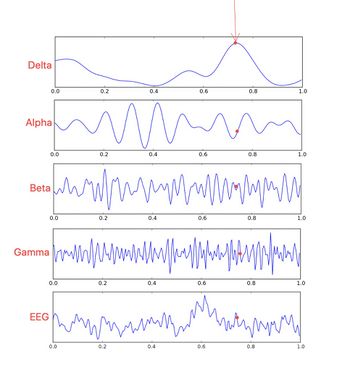
To stay on the neurophysiological theme, let's consider EEG electroencephalography. The measuring instrument basically measures nothing more than the difference in ionic electric potential 'dipole' that moves at sustained speeds here and there between the neural interconnections (Lagrangian coordinates) ^[10]). Figure 4

Well, here we introduce the quantum-like concept: if we observe the state of the brain through an EEG measurement we can only say that in a situation of this type the EEG state is nothing more than a superposition of mixed states which are essentially at least the 5 frequencies of wave $(\delta ,\theta ,\alpha ,\beta ,\gamma )$ depicted in figure 4. (EEG trace)

With this measurement (if we consider the EEG trace at the bottom of Figure 4) it remains very difficult to extrapolate the real condition of integrity of a specific and restricted brain area even supported by sophisticated mathematical / statistical analysis methods such as Fourier transforms, Wavelets etc., because the uncertainty of the measurement increases considerably in relation to the measured volume amplitude, the neuronal discharge rate, the sampling frequency, etc.

The EEG is not only the result of a tonic activity of the neuronal pool but a space-time sum of synchronous (phasic) and asynchronous (tonic) neuronal activities which sometimes collide, canceling, among other things, parts of the EEG trace.

«Basically it is like trying to understand the origin of the sound of a flute in an orchestra while recognizing its presence.»

Unfortunately in the EEG measurement we have a form of uncertainty of the measurement data. This phenomenon has been defined as the analogous 'Heisenberg Indetermination' principle of the form, $\bigtriangleup x(t)\bigtriangleup p_{x}(t)\geqq K_{brain}$ in which $K_{brain}$ stands for uncertainty constant of the electroencephalographic measurement. The authors of this study^[11] found that their quantum-like model leads to a minimum value of uncertainty constant in $\bigtriangleup x(t)\bigtriangleup p_{x}(t)$ eand in $\bigtriangleup y(t)\bigtriangleup p_{y}(t)$ of $0,78\pm 0,41{\tfrac {cm^{2}}{4ms}}$ in the case of the EEG. ( see chapter 'Exploring electroencephalography with a model inspired by quantum mechanics'.

At this point we have two 'Observables' in an asymptomatic subject tested in time $t$ the one deriving from the system measurement ' $A$ ' (EEG) which from what has been said could return a data system integrity (data polluted by $K_{brain}$ ) and an observable '' $B$ ' corresponding to the state of health of the subject who turns out to be sick.

The reality observed according to this projection would make the two observables $A$ and $B$ incompatible.

In textbooks on quantum mechanics, it is commonly pointed out that the main distinguishing feature of quantum theory is the presence of 'incompatible observables'. Recall that two observables, as in our case, $A$ e $B$ , are incompatible if it is impossible to attribute joint values to them. In the probabilistic model, this leads to the impossibility of determining their 'joint probability' distribution (JPD). (see chapter 'Quantum-like modeling in biology with open quantum systems and instruments')

«after a premise of this type, how do we approach the diagnosis of our poor Mary Poppins?»
(.... we will see in the next chapters how the approach changes)

Bibliography & references

↑ Milton Packer. The Parable of Schrödinger's Cat and the Illusion of Statistical Significance in Clinical Trials. . Circulation. . 2019 Sep 9;140(10):799-800doi: 10.1161/CIRCULATIONAHA.
↑ Carlos E Rochitte. Cardiac MRI and CT: the eyes to visualize coronary arterial disease and their effect on the prognosis explained by the Schrödinger's cat paradox. Radiol Bras..Jan-Feb 2016;49(1):VII-VIII. doi: 10.1590/0100-3984.2016.49.1e2.
↑ Schrödinger's cat paradox
↑ Schrödinger, Erwin (November 1935). "Die gegenwärtige Situation in der Quantenmechanik (The present situation in quantum mechanics)". Naturwissenschaften. 23 (48): 807–812.
↑ Notation bra-ket
↑ Stefan Rinner, Ernst Werner: On the role of entanglement in Schrödinger's cat paradox, Central European Journal of Physics 02/2008; 6(1):178-183
↑ In fact, the apparatus imagined by Schrödinger is even more complex, because it does not simply include an atom and a cat . To be precise, the other elements, such as the Geiger counter and the cyanide vial, should also be considered, which are also macroscopic. But even with this addition, the conclusions of the reasoning are essentially the same.
↑ Scully et al: State reduction in quantum mechanics: a calculational example, Phys. Rep. 43, 485–498 (1978).
↑ S. Haroche: Entanglement, decoherence and the quantum/classical boundary Archiviato il 25 aprile 2014 in Internet Archive., Physics Today, July 1998.
↑ Bin-Qiang Chen, Bai-Xun Zheng, Chu-Qiao Wang, Wei-Fang Sun. Adaptive Sparse Detector for Suppressing Powerline Component in EEG Measurements. Front Public Health. 2021 May 7;9:669190. doi: 10.3389/fpubh.2021.669190. eCollection 2021.
↑ Nicholas J M Popiel, Colin Metrow, Geoffrey Laforge Adrian M Owen, Bobby Stojanoski, Andrea Soddu. Exploring electroencephalography with a model inspired by quantum mechanics. Sci Rep. 2021 Oct 5;11(1):19771. doi: 10.1038/s41598-021-97960-7.

[:2-1] Milton Packer. The Parable of Schrödinger's Cat and the Illusion of Statistical Significance in Clinical Trials. . Circulation. . 2019 Sep 9;140(10):799-800doi: 10.1161/CIRCULATIONAHA.

[2] Carlos E Rochitte. Cardiac MRI and CT: the eyes to visualize coronary arterial disease and their effect on the prognosis explained by the Schrödinger's cat paradox. Radiol Bras..Jan-Feb 2016;49(1):VII-VIII. doi: 10.1590/0100-3984.2016.49.1e2.

[3] Schrödinger's cat paradox

[4] Schrödinger, Erwin (November 1935). "Die gegenwärtige Situation in der Quantenmechanik (The present situation in quantum mechanics)". Naturwissenschaften. 23 (48): 807–812.

[5] Notation bra-ket

[6] Stefan Rinner, Ernst Werner: On the role of entanglement in Schrödinger's cat paradox, Central European Journal of Physics 02/2008; 6(1):178-183

[7] In fact, the apparatus imagined by Schrödinger is even more complex, because it does not simply include an atom and a cat . To be precise, the other elements, such as the Geiger counter and the cyanide vial, should also be considered, which are also macroscopic. But even with this addition, the conclusions of the reasoning are essentially the same.

[8] Scully et al: State reduction in quantum mechanics: a calculational example, Phys. Rep. 43, 485–498 (1978).

[9] S. Haroche: Entanglement, decoherence and the quantum/classical boundary Archiviato il 25 aprile 2014 in Internet Archive., Physics Today, July 1998.

[10] Bin-Qiang Chen, Bai-Xun Zheng, Chu-Qiao Wang, Wei-Fang Sun. Adaptive Sparse Detector for Suppressing Powerline Component in EEG Measurements. Front Public Health. 2021 May 7;9:669190. doi: 10.3389/fpubh.2021.669190. eCollection 2021.

[11] Nicholas J M Popiel, Colin Metrow, Geoffrey Laforge Adrian M Owen, Bobby Stojanoski, Andrea Soddu. Exploring electroencephalography with a model inspired by quantum mechanics. Sci Rep. 2021 Oct 5;11(1):19771. doi: 10.1038/s41598-021-97960-7.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]