La lógica del lenguaje probabilístico
La lógica del lenguaje probabilístico
Resumen
El texto trata sobre la lógica del lenguaje probabilístico aplicado al campo médico, destacando cómo la incertidumbre es una parte intrínseca de la práctica científica. A través de conceptos probabilísticos y estadísticos, se busca gestionar y comprender las incertidumbres relacionadas con la teoría y la práctica médica.
Se enfatiza el papel de la probabilidad en la relación entre teoría y observación, distinguiendo entre incertidumbre subjetiva y casualidad. La incertidumbre subjetiva concierne al estado de conocimiento y convicción de los individuos, mientras que la casualidad se refiere a la falta de una conexión certera entre causa y efecto.
En el enfoque médico, se discute la importancia de comprender y distinguir entre probabilidad subjetiva y objetiva. La probabilidad subjetiva refleja la convicción individual, mientras que la objetiva se basa en datos y pruebas empíricas.
Luego se profundiza en el concepto de análisis probabilístico-causal, que busca cuantificar la relación entre eventos y procesos aleatorios en el diagnóstico clínico. Se presenta una exposición detallada sobre cómo interpretar probabilidades condicionales y utilizar la partición de la relevancia causal para formular un diagnóstico diferencial.
Finalmente, se aborda el tema de la interdisciplinariedad en la investigación científica, destacando la importancia de un enfoque interdisciplinario para abordar problemas complejos. También se menciona la lógica difusa como una posible herramienta para gestionar la incertidumbre en contextos médicos.
Lógica del lenguaje probabilístico en medicina
Toda idea científica (ya sea en medicina, arquitectura, ingeniería, química o cualquier otra materia), cuando se pone en práctica, está sujeta a pequeños errores e incertidumbres. Las matemáticas, a través de la teoría de la probabilidad y la inferencia estadística, ayudan a controlar con precisión y, por lo tanto, a contener estas incertidumbres. Siempre hay que considerar que en todos los casos prácticos "los resultados también dependen de muchos otros factores externos a la teoría", ya sean condiciones iniciales y ambientales, errores experimentales u otros.
Todas las incertidumbres acerca de estos factores hacen que la relación teoría-observación sea probabilística. En el abordaje médico, hay dos tipos de incertidumbre que más pesan en el diagnóstico: la incertidumbre subjetiva y la casualidad.[1][2]Se vuelve esencial, por lo tanto, en este escenario distinguir entre estas dos incertidumbres y mostrar que el concepto de probabilidad tiene diferentes significados en estos dos contextos. Intentaremos exponer estos conceptos vinculando cada paso crucial con el enfoque clínico que se ha informado en los capítulos anteriores y, en particular, el enfoque en el contexto dental y neurológico en la lucha por la primacía del diagnóstico de nuestra querida Mary Poppins.
Incertidumbre subjetiva y casualità
Imaginemos preguntarle a Mary Poppins cuál de los dos colegas médicos, el dentista o el neurólogo, tiene razón.
La pregunta crearía una especie de agitación basada en la incertidumbre interna; por tanto, las nociones de certeza e incertidumbre se refieren a estados epistémicos subjetivos de los seres humanos y no a estados del mundo externo, porque en ese mundo no hay certeza ni incertidumbre. En este sentido, como hemos mencionado, hay un mundo interior y un mundo exterior a nosotros mismos que no responden a cánones de incertidumbre, sino de probabilidad.
Mary Poppins puede estar subjetivamente segura o insegura de si sufre TTM o una forma neuropática o neuromuscular de OP: esto porque la "incertidumbre" es un estado epistémico subjetivo por debajo del umbral del conocimiento y la creencia; de ahí el término.
Incertidumbre subjetiva
Sin duda el término ‘subjetivo’ asusta a muchos, especialmente a quienes pretenden ejercer la ciencia persiguiendo el saludable ideal de ‘objetividad’, tal y como el sentido común percibe este término. Es, por tanto, oportuno hacer algunas aclaraciones sobre el uso de este término en este contexto:
- ‘Subjetivo’ indica que la evaluación de probabilidad depende del estado de información del individuo que la realiza.
- 'Subjetivo' no significa arbitrario
La llamada “objetividad”, tal como la perciben quienes están fuera de la investigación científica, se define cuando una comunidad de seres racionales comparte el mismo estado de información. Pero incluso en este caso, uno debería hablar más propiamente de "intersubjetividad" (es decir, el intercambio, por parte de un grupo, de opiniones subjetivas).
En los casos clínicos, precisamente porque los pacientes rara vez poseen nociones avanzadas de medicina, se debe considerar la incertidumbre subjetiva. Vivir con incertidumbre requiere que utilicemos un enfoque probabilístico.
Casualidad
La casualidad indica la falta de una cierta conexión entre causa y efecto. La incertidumbre de una estrecha unión entre la fuente y el fenómeno es uno de los problemas más adversos para determinar un diagnóstico.
En un caso clínico un fenómeno Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A(x)} (como por ejemplo una maloclusión, una mordida cruzada, una mordida abierta, etc...) se asocia aleatoriamente con otro fenómeno Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B(x)} (como la degeneración ósea de la ATM); cuando haya excepciones para las que la proposición lógica Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A(x) \rightarrow B(x)} no siempre sea verdadera (pero lo es la mayor parte del tiempo), diremos que la relación Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A(x) \rightarrow B(x)} no siempre es cierto, pero es probable.
Probabilidad subjetiva y objetiva
En este capítulo, algunos temas ya tratados en el fantástico libro de Kazem Sadegh-Zadeh[3], que aborda el problema de la lógica del lenguaje médico, son retomadas y remodelamos su contenido refiriéndolas a nuestro caso clínico de Mary Poppins, para acercar nuestra comprensión a los contextos odontológicos.
Se dice que los eventos aleatorios y subjetivamente inciertos son probables; en consecuencia, la casualidad y la incertidumbre se tratan como probabilidades cualitativas, comparativas o cuantitativas.
Para aclarar este concepto, volvamos al ejemplo de Mary Poppins. Un médico, habiendo escuchado sus síntomas, podrá decir que:
Para aclarar este concepto, volvamos al ejemplo de Mary Poppins. Un médico, habiendo escuchado sus síntomas, podrá decir que:
- Mary Poppins probablemente sufre de TMD (término cualitativo).
- Es más probable que Mary Poppins tenga TTM que OP neuropática (término comparativo: número de casos diagnosticados de TTM versus nOP.
- La probabilidad de que Mary Poppins tenga TTM es 0,15 (término cuantitativo, relativo a la población).
Probabilidad subjetiva
En un contexto de incertidumbre subjetiva humana, los datos probabilísticos, cualitativos, comparativos y/o cuantitativos pueden ser interpretados como una medida de incertidumbre subjetiva por el médico, para hacer que los "estados de convicción" sean numéricamente representables.
Por ejemplo, decir que "la probabilidad de que Mary Poppins esté afectada por TTM es 0,15 de los casos" es lo mismo que decir "en la medida del 15%, creo que Mary Poppins está afectada por TTM"; lo que significa que el grado de convicción es el grado de probabilidad subjetiva.
Probabilidad objetiva
Por otro lado, los eventos y procesos aleatorios no pueden ser descritos por procesos deterministas en la forma 'si A entonces B'. Las estadísticas se utilizan para cuantificar la frecuencia de asociación entre A y B y para representar las relaciones entre ellos como un grado de probabilidad que introduce el grado de probabilidad objetiva.
A raíz de la creciente probabilización de la incertidumbre y la aleatoriedad en la medicina desde el siglo XVIII, el término "probabilidad" se ha convertido en un elemento respetado del lenguaje, la metodología y la epistemología médica. Desafortunadamente, los dos tipos de probabilidad, la probabilidad subjetiva y la probabilidad objetiva, no se diferencian con precisión en medicina, y lo mismo sucede en otras disciplinas. El hecho fundamental sigue siendo que el significado más importante que la teoría de la probabilidad ha generado en medicina, particularmente en los conceptos de probabilidad en etiología, epidemiología, diagnóstico y terapia, es su contribución a nuestra comprensión y representación de la causalidad biológica.
Análisis probabilístico-causal
De estas premisas se desprende que el diagnóstico clínico se realiza mediante el denominado método hipotético-deductivo denominado DN[4] (modelo deductivo-nomológico)[5]. Pero esto no es realista, ya que el conocimiento médico utilizado en la toma de decisiones clínicas difícilmente contiene leyes deterministas causales que permitan explicaciones causales y, por tanto, formular diagnósticos clínicos, entre otras cosas en el contexto del especialista. Intentemos analizar nuevamente el caso de nuestra Mary Poppins, esta vez intentando un enfoque probabilístico-causal.
Consideremos un número Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} de personas, incluidas las personas que informan dolor orofacial que generalmente tienen degeneración ósea de la articulación temporomandibular. Sin embargo, también pueden existir otras causas aparentemente no relacionadas. Debemos traducir matemáticamente la 'relevancia' que estas incertidumbres causales tienen para determinar un diagnóstico.
La relevancia casual
Para ello consideramos el grado de relevancia causal Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (cr)} de un evento Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_1} con respecto a un evento Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_2} donde:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_1} = Pacientes con degeneración ósea de la articulación temporomandibular.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_2} = Pacientes que refieren dolor orofacial.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_3} = Pacientes sin degeneración ósea de la articulación temporomandibular.
Usaremos la probabilidad condicional Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(A \mid B)} , que es la probabilidad de que el evento Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} ocurra solo después de que el evento Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B} ya haya ocurrido.
Con estas premisas la relevancia causal Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle cr} de la muestra Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} de pacientes es:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle cr=P(E_2 \mid E_1)- P(E_2 \mid E_3)}
dónde
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(E_2 \mid E_1)} indica la probabilidad de que algunas personas (entre Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} consideradas) padezcan Dolor Orofacial causado por la degeneración ósea de la Articulación Temporomandibular,
aunque
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(E_2 \mid E_3)} indica la probabilidad de que otras personas (siempre entre Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} considerados) padezcan Dolor Orofacial condicionado por algo distinto a la degeneración ósea de la Articulación Temporomandibular.
Dado que todas las probabilidades sugieren que Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(A \mid B)} es un valor entre Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0 } y Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1 } , el parámetro Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (cr)} será un número que está entre Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -1 } y Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1 }
Los significados que le podemos dar a este número son los siguientes:
- tenemos los casos extremos (que en realidad nunca se dan) que son:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle cr=1} indicando que la única causa del dolor orofacial es la degeneración ósea de la ATM,
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle cr=-1} lo que indica que la causa del dolor orofacial nunca es la degeneración ósea de la ATM sino otra cosa,
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle cr=0} indicando que la probabilidad de que el dolor orofacial sea causado por la degeneración ósea de la ATM o de otra manera es exactamente la misma,
- y los casos intermedios (que son los realistas)
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle cr>0} lo que indica que la causa del dolor orofacial es más probable que sea la degeneración ósea de la ATM,
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle cr<0} lo que indica que la causa del dolor orofacial probablemente no sea la degeneración ósea de la ATM.
Segundo Enfoque Clínico
(pasa el cursor sobre las imágenes)
Sea entonces Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(D)} la probabilidad de encontrar, en la muestra de nuestras Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} personas, individuos que presenten los elementos pertenecientes al mencionado conjunto Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D=\{\delta_1,\delta_2,...,\delta_n\}}
Para aprovechar la información proporcionada por este conjunto de datos, se introduce el concepto de partición de relevancia causal:
La partición de la relevancia causal
- Siempre sea Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} el número de personas sobre las que tenemos que realizar los análisis, si dividimos (basado en ciertas condiciones como se explica a continuación) este grupo en Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} subconjuntos Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_i} con Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i=1,2,\dots,k} , se crea un grupo que se denomina "conjunto de partición" Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi = \{C_1, C_2,\dots,C_k \} \qquad \qquad \text{con} \qquad \qquad C_i \subset n , }
donde con el simbolismo Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_i \subset n } indica que la subclase Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_i} está contenida en Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n}
La partición Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi} , para que sea definida como una partición de relevancia causal, debe tener estas propiedades:
- Para cada subclase Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_i} debe aplicarse la condición Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle rc=P(D \mid C_i)- P(D )\neq 0, } es decir la probabilidad de encontrar en el subgrupo Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_i} una persona que presente los síntomas, signos clínicos y elementos pertenecientes al conjuntoFailed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D=\{\delta_1,\delta_2,...,\delta_n\}} . Se dice que una partición causalmente relevante de este tipo es homogénea.
- Cada subconjunto Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_i} debe ser 'elemental', es decir, no debe dividirse más en otros subconjuntos, porque si estos existieran no tendrían relevancia causal.
Ahora supongamos, por ejemplo, que la población muestra Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} , a la que pertenece nuestra buena paciente Mary Poppins, es una categoría de sujetos de 20 a 70 años. Suponemos también que en esta población tenemos a quienes presentan los elementos pertenecientes a la conjunto de datos Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D=\{\delta_1,.....\delta_n\}} que corresponden a las pruebas de laboratorio mencionadas anteriormente y precisamente en 'The logic of classical language'.
Supongamos que en una muestra de 10.000 sujetos de 20 a 70 tendremos una incidencia de 30 sujetos Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p(D)=0.003} mostrando signos clínicos Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta_1} y Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta_4 } . Preferimos utilizar estos informes para la demostración del proceso probabilístico porque en la literatura los datos referentes a Los signos y síntomas clínicos de los trastornos temporomandibulares tienen una variación demasiado amplia y una incidencia demasiado alta en nuestra opinión.[6][7][8][9][10][11]
Un ejemplo de una partición con presunta probabilidad en la que la degeneración de la ATM (Deg.TMJ) se produce junto con los trastornos temporomandibulares (TMD) sería el siguiente:
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(D| Deg.TMJ \cap TMDs)=0.95 \qquad \qquad \; } | dónde | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \C_1 \equiv Deg.TMJ \cap TMDs} | |||
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(D| Deg.TMJ \cap noTMDs)=0.3 \qquad \qquad \quad } | dónde | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_2\equiv Deg.TMJ \cap noTMDs} | |||
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(D| no Deg.TMJ \cap TMDs)=0.199 \qquad \qquad \; } | dónde | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_3\equiv no Deg.TMJ \cap TMDs} | |||
| dónde | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_4\equiv noDeg.TMJ \cap noTMDs} |
- «Una partición homogénea proporciona lo que estamos acostumbrados a llamar Diagnóstico Diferencial.»
Situaciones clínicas
Estas probabilidades condicionales demuestran que cada una de las cuatro subclases de la partición es causalmente relevante para los datos del paciente Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D=\{\delta_1,.....\delta_n\}} en la muestra de población Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle PO} . Dada la partición antes mencionada de la clase de referencia, tenemos las siguientes situaciones clínicas:
- Mary Poppins Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \in} Degeneración de la articulación temporomandibular Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cap} Trastornos temporomandibulares
- Mary Poppins Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \in} degeneración de la articulación temporomandibular Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cap} no Trastornos temporomandibulares
- Mary Poppins Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \in} sin degeneración de la articulación temporomandibular Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cap} Trastornos temporomandibulares
- Mary Poppins Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \in} sin degeneración de la articulación temporomandibular Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cap} sin trastornos temporomandibulares
Para llegar al diagnóstico final anterior, realizamos un análisis probabilístico-causal del estado de salud de Mary Poppins cuyos datos iniciales fueron Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D=\{\delta_1,.....\delta_n\}} .
En general, podemos referirnos a un proceso lógico en el que examinamos los siguientes elementos:
- un individuo: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a}
- su conjunto de datos inicialFailed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D=\{\delta_1,.....\delta_n\}}
- una muestra de población Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} a la que pertenece,
- una probabilidad básica Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(D)=0,003}
En este punto conviene introducir argumentos demasiado especializados que alejarían al lector del tema pero que tienen una gran importancia epistémica por lo que intentaremos extraer el hilo lógico más descrito del concepto Analysandum/Analysans.
El análisis probabilístico-causal de Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D=\{\delta_1,.....\delta_n\}} es entonces un par de las siguientes formas lógicas (Analysandum / Analysans[12]):
- Analysandum Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \{P(D),a\}} : es una forma lógica que contiene dos parámetros: probabilidad Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(D)} de seleccionar una persona que tenga los síntomas y elementos pertenecientes al conjunto Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D=\{\delta_1,\delta_2,...,\delta_n\}} , y el individuo genérico Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} que es propenso a esos síntomas.
- Analysan Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \{\pi,a,KB\}} : es una forma lógica que contiene tres parámetros: la partición Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi} , el individuo genérico Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} perteneciente a la muestra poblacional Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} y Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle KB} (Base de Conocimiento) que incluye un conjunto de Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n>1} enunciados de probabilidad condicionada.
Por ejemplo, se puede concluir que el diagnóstico definitivo es el siguiente:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(D| Deg.TMJ \cap TMDs)=0.95} - esto significa que nuestra Mary Poppins está afectada en un 95% por TTM, ya que tiene una degeneración de la Articulación Temporomandibular además de los datos positivos Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D=\{\delta_1,.....\delta_n\}}
Consideraciones finales
Tomamos un camino largo y tortuoso para comprender mejor la complejidad que enfrenta el colega que lucha con la responsabilidad ética muy pesada de hacer un diagnóstico. Sin embargo, esta tarea se vuelve aún más compleja cuando necesitamos ser minuciosos y cuidadosos al realizar un diagnóstico diferencial.
Aquí entramos en un tema delicado, que está conectado con los contenidos epistemológicos y que en primer lugar fue relatado en el "Introduction". Nosotras estamos hablando de:
- Interdisciplinariedad
En la política científica, generalmente se reconoce que la resolución de problemas basada en la ciencia requiere investigación interdisciplinaria (IDR), como propone el proyecto de la UE llamado Horizonte 2020[13]. En un estudio reciente, los autores se centran en la pregunta de por qué los investigadores tienen dificultades cognitivas y epistémicas para realizar IDR. Se cree que la pérdida de interés filosófico en la epistemología de la investigación interdisciplinaria es causada por un paradigma filosófico de la ciencia denominado “Paradigma de la Física de la Ciencia”, que impide reconocer cambios importantes en la IDR tanto en la filosofía de la ciencia como en la investigación.
El paradigma filosófico alternativo propuesto, llamado 'Paradigma de Ingeniería de la Ciencia', hace suposiciones filosóficas alternativas sobre aspectos como el propósito de la ciencia, el carácter del conocimiento, los criterios epistémicos y pragmáticos para la aceptación del conocimiento y el papel de las herramientas tecnológicas. En consecuencia, los investigadores científicos necesitan los llamados andamios metacognitivos para ayudarlos en el análisis y reconstrucción de cómo se construye el "conocimiento" en diferentes disciplinas.
En la investigación interdisciplinaria, los andamios metacognitivos ayudan a la comunicación interdisciplinaria a analizar y articular cómo la disciplina construye conocimiento.[14][15]
Este concepto está ligado al tema tratado anteriormente en el que el colega debe ser consciente de su propia 'Incertidumbre Subjetiva' (debido a un lenguaje lógico clásico 'enfermo o sano') y de la 'Incertidumbre Objetiva' (debido a un lenguaje lógico probabilístico ' probablemente enfermo o probablemente sano'). No es complicado probar esta afirmación: la incertidumbre de la que estamos hablando deriva del hecho de que los elementos, afirmaciones, datos, clases y subclases mencionados y que construyen el aparato de la lógica del lenguaje probabilístico: Analysandum Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \{P(D),a\}} y Analysan Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \{\pi,a,KB\}} son elementos que existen en un mundo específico, y en este caso en un contexto odontológico en el que el elemento Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle KB} del proceso indica indiscutiblemente un "conocimiento básico" sólo en un contexto odontológico específico.
Esta conclusión confirmada por el dentista fue la siguiente:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(D| Deg.TMJ \cap TMDs)=0.95}
o mejor: es mi creencia del 95% que Mary Poppins está afectada por TTM ya que tiene una degeneración de la articulación temporomandibular además de la positividad de los datos Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D=\{\delta_1,\dots\delta_n\}} . Pero algo extraño sucede porque de la nada, un investigador, que utiliza 'andamios metacognitivos'[16] para una implementación en el análisis y reconstrucción de cómo se construye el 'conocimiento' en diferentes disciplinas, exige al odontólogo una respuesta a la siguiente pregunta:
«¿Existe otro mundo o contexto, paralelo al tuyo, en el que además de los datos D haya otros datos desconocidos para ti?»
|
y aumente la dosis: someta a Mary Poppins a las siguientes pruebas electrofisiológicas del trigémino, etiquételas como hicimos anteriormente para los datos establecidos Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D=\{\delta_1,\dots\delta_n\}}
generar otro conjunto que contenga un número Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m}
de datos desconocidos (no pertenecientes a la rama puramente dental) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C=\{\gamma_1,\dots\gamma_m\}}
creando así un conjunto completamente nuevo que llamaremos Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{unknow}= D+C=\{\delta_1,\dots,\delta_n,\gamma_1,\dots,\gamma_m\}}
(called Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{unknown}}
precisamente por la presencia de datos desconocidos para el contexto odontológico).
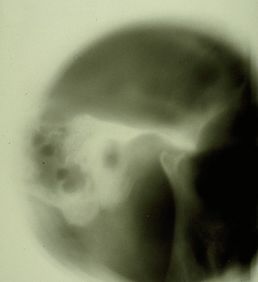
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta_1=} Informe radiológico positivo de la ATM en la Figura 2
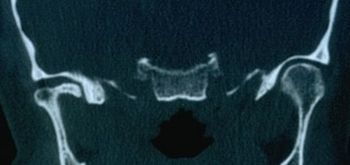
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta_2=} Informe de TC positivo de la ATM en la Figura 3
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta_3=} Informe axiográfico positivo de los trazos condilares en la Figura 4
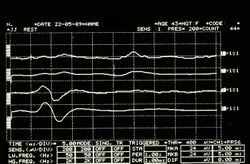
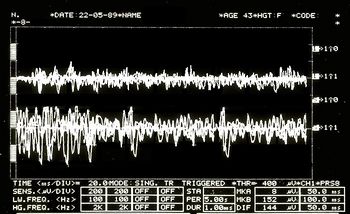
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta_4=} Patrón de interferencia EMG asimétrico en la Figura 5
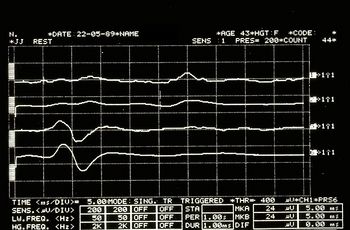
Tirón de mandíbula en la figura 6
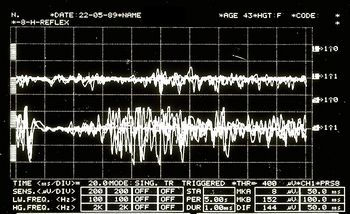
Período de silencio mecánico en la figura 7
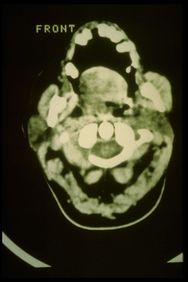
TC del músculo masetero derecho en la Figura 8
Tercer enfoque clínico
(pasa el cursor sobre las imágenes)
De esta manera se ha demostrado que, inevitablemente,
Al explorar esta línea perimetral del contexto especializado, crearemos un área cercana a ella que llamaremos 'zona difusa' o 'lógica difusa' que discutiremos en el próximo capítulo.
«... por lo que parece ni con una lógica de lenguaje probabilístico podremos definir un diagnóstico exacto.»
(de hecho, por esta razón también deberíamos considerar Fuzzy Logic Language) |
- ↑ Vázquez-Delgado E, Cascos-Romero J, Gay-Escoda C, «Myofascial pain associated to trigger points: a literature review. Part 2: differential diagnosis and treatment», in Med Oral Patol Oral Cir Bucal, 2007».
PMID:20173729
DOI:10.4317/medoral.15.e639 - ↑ Thoppay J, Desai B, «Oral burning: local and systemic connection for a patient-centric approach», in EPMA J, 2019».
PMID:30984309 - PMCID:PMC6459460
DOI:10.1007/s13167-018-0157-3 - ↑ Sadegh-Zadeh Kazem, «Handbook of Analytic Philosophy of Medicine», Springer, 2012, Dordrecht».
ISBN: 978-94-007-2259-0
DOI:10.1007/978-94-007-2260-6 . - ↑ Sarkar S, «Nagel on Reduction», in Stud Hist Philos Sci, 2015».
PMID:26386529
DOI:10.1016/j.shpsa.2015.05.006 - ↑ DN model of scientific explanation, also known as Hempel's model, Hempel–Oppenheim model, Popper–Hempel model, or covering law model
- ↑ Pantoja LLQ, De Toledo IP, Pupo YM, Porporatti AL, De Luca Canto G, Zwir LF, Guerra ENS, «Prevalence of degenerative joint disease of the temporomandibular joint: a systematic review», in Clin Oral Investig, 2019».
PMID:30311063
DOI:10.1007/s00784-018-2664-y - ↑ De Toledo IP, Stefani FM, Porporatti AL, Mezzomo LA, Peres MA, Flores-Mir C, De Luca Canto G, «Prevalence of otologic signs and symptoms in adult patients with temporomandibular disorders: a systematic review and meta-analysis», in Clin Oral Investig, 2017».
PMID:27511214
DOI:10.1007/s00784-016-1926-9 - ↑ Bonotto D, Penteado CA, Namba EL, Cunali PA, Rached RN, Azevedo-Alanis LR, «Prevalence of temporomandibular disorders in rugby players», in Gen Dent».
PMID:31355769 - ↑ da Silva CG, Pachêco-Pereira C, Porporatti AL, Savi MG, Peres MA, Flores-Mir C, De Luca Canto G, «Prevalence of clinical signs of intra-articular temporomandibular disorders in children and adolescents: A systematic review and meta-analysis», in Am Dent Assoc, 2016». - PMCID:26552334
DOI:10.1016/j.adaj.2015.07.017 - ↑ Gauer RL, Semidey MJ, «Diagnosis and treatment of temporomandibular disorders», in Am Fam Physician, 2015».
PMID:25822556 - ↑ Kohlmann T, «Epidemiology of orofacial pain», in Schmerz, 2002».
PMID:12235497
DOI:10.1007/s004820200000 - ↑ Westmeyer H, «The diagnostic process as a statistical-causal analysis», in APA, 1975».
DOI:10.1007/BF00139821
This is an Open Access resource! - ↑ European Union, Horizon 2020
- ↑ Boon M, Van Baalen S, «Epistemology for interdisciplinary research - shifting philosophical paradigms of science», in Eur J Philos Sci, 2019».
DOI:10.1007/s13194-018-0242-4 9(1):16. - ↑ Boon M, «An engineering paradigm in the biomedical sciences: Knowledge as epistemic tool», in Prog Biophys Mol Biol, 2017».
DOI:10.1016/j.pbiomolbio.2017.04.001 - ↑ Boon M, Van Baalen S, «Epistemology for interdisciplinary research - shifting philosophical paradigms of science», in Eur J Philos Sci, 2019».
PMID:30873248 - PMCID:PMC6383598
DOI:10.1007/s13194-018-0242-4
This is an Open Access resource!
particularly focusing on the field of the neurophysiology of the masticatory system