Fuzzy language logic
Fuzzy language logic
Abstract: In this chapter, we delve into the cognitive limits of diagnostic reasoning, focusing on how knowledge in medical science is bound by time and context, represented by two parameters: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle KB_t} (time-dependent knowledge base) and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle KB_c} (context-dependent knowledge base). These parameters emphasize how scientific knowledge evolves and is shaped by the specific context in which it operates. Through practical examples, such as research on Temporomandibular Disorders (TMD) and Orofacial Pain (OP), we illustrate the interconnectedness of scientific fields and the significant drop in knowledge integration when topics are combined.
The discussion moves from the limitations of classical logic to the broader framework of probabilistic reasoning, and eventually to fuzzy logic. We examine how classical logic, with its binary nature, is inadequate for medical diagnosis, where uncertainty is inherent. By introducing fuzzy logic, a multivalent approach, we show how it is better suited to handling the complexities and uncertainties of clinical cases, such as that of Mary Poppins.
Fuzzy logic allows for a more flexible representation of truth, enabling the partial inclusion of concepts within sets, and thus reducing diagnostic errors. The chapter emphasizes the importance of expanding our knowledge base across different contexts and integrating interdisciplinary perspectives, particularly in dentistry and neurophysiology. Finally, it concludes with a call for continued exploration of system logic, setting the stage for the following chapter on the "System Language Logic."
Introduction
We have come this far because, as colleagues, are very often faced with responsibilities and decisions that are very difficult to take and issues such as conscience, intelligence and humility come into play. In such a situation, however, we are faced with two equally difficult obstacles to manage that of one Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle KB} (Knowledge Basis), as we discussed in the chapter ‘Logic of probabilistic language’, limited in the time that we codify in Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle KB_t} and one Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle KB} limited in the specific context (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle KB_c} ). These two parameters of epistemology characterize the scientific age in which we live. Also, both that the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle KB_c} are dependent variables of our phylogeny, and, in particular of our conceptual plasticity and attitude to change.[1]
(I'll give you a practical example)
How much research has been produced on the topic 'Fuzzy logic'?
Pubmed responds with 2862 articles in the last 10 years[2][3], so that we can say that ours is current and is sufficiently updated. However, if we wanted to focus attention on a specific topic like ‘Temporomandibular Disorders’, the database will respond with as many as 2,235 articles. [4] Hence, if we wanted to check another topic like ‘Orofacial Pain’, Pubmed gives us 1,986 articles.[5] This means that the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle KB_t} for these three topics in the last 10 years it has been sufficiently updated.
If, now, we wanted to verify the interconnection between the topics, we will notice that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle KB_c} in the contexts will be the following:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle KB_c=} 'Temporomandibular disorders AND Orofacial Pain'Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rightarrow} 9 articles in the last 10 years[6]
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle KB_c=} 'Temporomandibular disorders AND Orofacial Pain AND Fuzzy logic' 0 articles in the last 10 years[7]
The example means that the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle KB_t} is relatively up-to-date individually for the three topics while it decreases dramatically when the topics between contexts are merged and specifically to 9 articles for Point 1 and even to 0 articles for Point 2. So, the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle KB_t} is a time dependent variable while the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle KB_c} is a cognitive variable dependent on our aptitude for the progress of science, as already mentioned—among other things—in the chapter ‘Introduction’.
(Wait and see)
We ended the previous chapter by asserting that the logic of a classical language and subsequently probabilistic logic have helped us a lot in the progress of medical science and diagnostics but implicitly carry within themselves the limits of their own logic of language, which limits the vision of the biological universe. We also verified that with the logic of a classical language—so to speak, Aristotelian—the logical syntax that is derived from it in the diagnostics of our Mary Poppins limits, in fact, the clinical conclusion.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{a \in x \mid \forall \text{x} \; A(\text{x}) \rightarrow {B}(\text{x}) \vdash A( a)\rightarrow B(a) \}} (see chapter The logic of the classic language),
argues that: "every normal patient Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \forall\text{x}} which is positive on the radiographic examination of the TMJ Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{\mathcal{A}}(\text{x})} has TMDsFailed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rightarrow\mathrm{\mathcal{B}}(\text{x})} , as a direct consequence Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vdash} Mary Poppins being positive (and also being a "normal" patient) on the TMJ x-ray Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A(a)} then Mary Poppins is also affected by TMDs Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rightarrow \mathcal{B}(a)}
The limitation of the logical path that has been followed has led us to undertake an alternative path, in which the bivalence or binary nature of classical language logic is avoided and a probabilistic model is followed. The dentist colleague, in fact, changed the vocabulary and preferred a conclusion like:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(D| Deg.TMJ \cap TMDs)=0.95}
and which is, that our Mary Poppins is 95% affected by TMDs since she has a degeneration of the temporomandibular joint supported by the positivity of the data Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D=\{\delta_1,\dots\delta_4\}} in a population sample Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} . However, we also found that in the process of constructing probabilistic logic (Analysandum Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \{P(D),a\}} ) which allowed us to formulate the aforementioned differential diagnostic conclusions and choose the most plausible one, there is a crucial element to the whole AnalysandFailed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \{\pi,a,KB\}} represented by the term Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle KB} which indicates, specifically, a 'Knowledge Base' of the context on which the logic of probabilistic language is built.
We therefore concluded that perhaps the dentist colleague should have become aware of his own 'Subjective Uncertainty' (affected by TMDs or nOP?) and 'Objective Uncertainty' (probably more affected by TMDs or nOP?).
Why have we come to these critical conclusions?
For a widely shared form of the representation of reality, supported by the testimony of authoritative figures who confirm its criticality. This has given rise to a vision of reality which, at first glance, would seem unsuitable for medical language; in fact, expressions such as ‘about 2’ or ‘moderately’ can arouse legitimate perplexity and seem an anachronistic return to pre-scientific concepts. On the contrary, however, the use of fuzzy numbers or assertions allows scientific data to be treated in contexts in which one cannot speak of ‘probability’ but only of ‘possibility’.[8]
Fuzzy truth
In the ambitious attempt to mathematically translate human rationality, it was thought in the mid-twentieth century to expand the concept of classical logic by formulating fuzzy logic. Fuzzy logic concerns the properties that we could call ‘graduality’, i.e., which can be attributed to an object with different degrees. Examples are the properties ‘being sick’, ‘having pain’, ‘being tall’, ‘being young’, and so on.
Mathematically, fuzzy logic allows us to attribute to each proposition a degree of truth between Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1} . The most classic example to explain this concept is that of age: we can say that a new-born has a ‘degree of youth’ equal to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1} , an eighteen-year-old equal to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0,8} , a sixty-year-old equal to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0,4} , and so on
In the context of classical logic, on the other hand, the statements:
- a ten-year-old is young
- a thirty-year-old is young
are both true. However, in the case of classical logic (which allows only the two true or false data), this would mean that the infant and the thirty-year-old are equally young. Which is obviously wrong.
The importance and the charm of fuzzy logic arise from the fact that it is able to translate the uncertainty inherent in some data of human language into mathematical formalism, coding ‘elastic’ concepts (such as almost high, fairly good, etc.), in order to make them understandable and manageable by computers.
Set theory
As mentioned in the previous chapter, the basic concept of fuzzy logic is that of multivalence, i.e., in terms of set theory, of the possibility that an object can belong to a set even partially and, therefore, also to several sets with different degrees. Let us recall from the beginning the basic elements of the theory of ordinary sets. As will be seen, in them appear the formal expressions of the principles of Aristotelian logic, recalled in the previous chapter.
Quantifiers
- Membership: represented by the symbol Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \in } (belongs), - for example the number 13 belongs to the set of odd numbers Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \in } Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 13\in Odd }
- Non-membership: represented by the symbol Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \notin } (It does not belong)
- Inclusion: Represented by the symbol Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \subset} (is content), - for example the whole Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} it is contained within the larger set Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A \subset U} (in this case it is said that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} is a subset of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U} )
- Universal quantifier, which is indicated by the symbol Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \forall} (for each)
- Demonstration, which is indicated by the symbol Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mid} (such that)
Set operators
Given the whole universe Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U} we indicate with Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} its generic element so that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x \in U} ; then, we consider two subsets Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} and internal to so that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A \subset U} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B \subset U}
The theory of fuzzy language logic is an extension of the classical theory of sets in which, however, the principles of non-contradiction and the excluded third are not valid. Remember that in classical logic, given the set Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} and its complementary Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bar{A}} , the principle of non-contradiction states that if an element belongs to the whole Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} it cannot at the same time also belong to its complementary ; according to the principle of the excluded third, however, the union of a whole Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} and its complementary Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bar{A}} constitutes the complete universe Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U} .
In other words, if any element does not belong to the whole, it must necessarily belong to its complementary.
Fuzzy set Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tilde{A}} and membership function Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu_{\displaystyle {\tilde {A}}}(x)}
We choose - as a formalism - to represent a fuzzy set with the 'tilde':Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tilde{A}} . A fuzzy set is a set where the elements have a 'degree' of belonging (consistent with fuzzy logic): some can be included in the set at 100%, others in lower percentages.
To mathematically represent this degree of belonging is the function Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu_{\displaystyle {\tilde {A}}}(x)} called 'Membership Function'. The function Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu_{\displaystyle {\tilde {A}}}(x)} is a continuous function defined in the interval Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [0;1]} where it is:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu_ {\tilde {A}}(x) = 1\rightarrow } if Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} is totally contained in Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} (these points are called 'nucleus', they indicate plausible predicate values).
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu_ {\tilde {A}}(x) = 0\rightarrow } if Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} is not contained in Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0<\mu_ {\tilde {A}}(x) < 1 \;\rightarrow } if Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} is partially contained in Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} (these points are called 'support', they indicate the possible predicate values).
The graphical representation of the function Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu_{\displaystyle {\tilde {A}}}(x)} can be varied; from those with linear lines (triangular, trapezoidal) to those in the shape of bells or 'S' (sigmoidal) as depicted in Figure 1, which contains the whole graphic concept of the function of belonging.[9][10]
The support set of a fuzzy set is defined as the zone in which the degree of membership results Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0<\mu_ {\tilde {A}}(x) < 1} ; on the other hand, the core is defined as the area in which the degree of belonging assumes value Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu_ {\tilde {A}}(x) = 1}
The 'Support set' represents the values of the predicate deemed possible, while the 'core' represents those deemed more plausible.
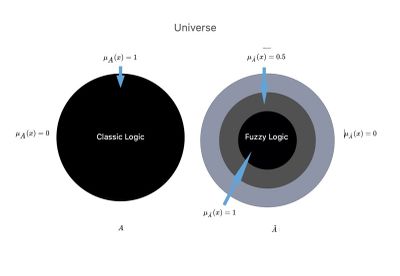
If Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {A}} represented a set in the ordinary sense of the term or classical language logic previously described, its membership function could assume only the values Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1} or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0} , depending on whether the element Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} belongs to the whole or not, as considered. Figure 2 shows a graphic representation of the crisp (rigidly defined) or fuzzy concept of membership, which clearly recalls Smuts's considerations.[11]
Let us go back to the specific case of our Mary Poppins, in which we see a discrepancy between the assertions of the dentist and the neurologist and we look for a comparison between classical logic and fuzzy logic:
Figure 2: Let us imagine the Science Universe Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U} in which there are two parallel worlds or contexts, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {A}} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tilde{A}} .
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {A}=} In the scientific context, the so-called ‘crisp’, and we have converted into the logic of Classic Language, in which the physician has an absolute scientific background information Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle KB} with a clear dividing line that we have named Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle KB_c} .
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tilde{A}=} In another scientific context called ‘fuzzy logic’, and in which there is a union between the subset Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {A}} in Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tilde{A}} that we can go so far as to say: union between Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle KB_c} .
We will remarkably notice the following deductions:
- Classical Logic in the Dental Context Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {A}} in which only a logical process that gives as results Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu_{\displaystyle {{A}}}(x)= 1 } will be possible, or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu_{\displaystyle {{A}}}(x)= 0 } being the range of data Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D=\{\delta_1,\dots,\delta_4\}} reduced to basic knowledge Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle KB} in the set Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {A}} . This means that outside the dental world there is a void and that term of set theory is written precisely Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu_{\displaystyle {{A}}}(x)= 0 } and which is synonymous with a high range of:
- Fuzzy logic in a dental context Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tilde{A}}
in which they are represented beyond the basic knowledge Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle KB}
of the dental context also those partially acquired from the neurophysiological world Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0<\mu_ {\tilde {A}}(x) < 1}
will have the prerogative to return a result Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu_\tilde{A}(x)= 1 }
and a result Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0<\mu_ {\tilde {A}}(x) < 1}
because of basic knowledge Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle KB}
which at this point is represented by the union of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle KB_c}
dental and neurological contexts. The result of this scientific-clinical implementation of dentistry would allow a «Reduction of differential diagnostic error»
Consideraciones finales
Los temas que podían distraer la atención del lector eran, de hecho, esenciales para demostrar el mensaje. Normalmente, en efecto, cuando cualquier mente más o menos brillante se permite arrojar una piedra al estanque de la Ciencia, se genera una onda expansiva, propia del período de la ciencia extraordinaria de Kuhn, contra la que se pelean la mayoría de los miembros de la comunidad científica internacional. De buena fe podemos decir que este fenómeno —en lo que se refiere a los temas que aquí abordamos— está bien representado en la premisa al inicio del capítulo.
En estos capítulos, en realidad, se ha abordado un tema fundamental para la ciencia: la reevaluación, el peso específico que siempre se le ha dado al Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P-value} , la toma de conciencia de los contextos científico/clínicos , habiendo emprendido un camino más elástico de la Lógica Difusa que el Clásica, dándose cuenta de la extrema importancia del y en definitiva de la unión de los contextos para aumentar su capacidad diagnóstica.[12][13]
En el próximo capítulo estaremos listos para emprender un camino igualmente fascinante: nos conducirá al contexto de una lógica de Lenguaje de Sistemas, y nos permitirá profundizar nuestro conocimiento, ya no solo en la semiótica clínica, sino en la comprensión de la lógica de sistemas. funciones (recientemente se está evaluando en disciplinas neuromotoras para la enfermedad de Parkinson).[14]
En Masticationpedia, por supuesto, informaremos sobre el tema 'Inferencia del sistema' en el campo del sistema masticatorio, como podemos leer en el próximo capítulo titulado 'Lógica del sistema'.
- ↑ Takeuchi S, Okuda S, «Knowledge base toward understanding actionable alterations and realizing precision oncology», in Int J Clin Oncol, 2019».
PMID:30542800 - PMCID:PMC6373253
DOI:10.1007/s10147-018-1378-0
This is an Open Access resource! - ↑ Fuzzy logic on Pubmed
- ↑ All statistics collected following visits to the Pubmed site (https://pubmed.ncbi.nlm.nih.gov/). Last checked: December 2020.
- ↑ Temporomandibular Disorders in Pubmed
- ↑ Orofacial Pain in Pubmed
- ↑ Temporomandibular disorders AND Orofacial Pain in Pubmed
- ↑ "Temporomandibular disorders AND Orofacial Pain AND Fuzzy logic" in Pubmed
- ↑ Dubois D, Prade H, «Fundamentals of Fuzzy Sets», Kluwer Academic Publishers, 2000, Boston».
- ↑ Zhang W, Yang J, Fang Y, Chen H, Mao Y, Kumar M, «Analytical fuzzy approach to biological data analysis», in Saudi J Biol Sci, 2017».
PMID:28386181 - PMCID:PMC5372457
DOI:10.1016/j.sjbs.2017.01.027 - ↑ Lazar P, Jayapathy R, Torrents-Barrena J, Mol B, Mohanalin, Puig D, «Fuzzy-entropy threshold based on a complex wavelet denoising technique to diagnose Alzheimer disease», in Healthc Technol Lett, The Institution of Engineering and Technology, 2016».
PMID:30800318 - PMCID:PMC6371778
DOI:10.1049/htl.2016.0022 - ↑ •SMUTS J.C. 1926, Holism and Evolution, London: Macmillan.
- ↑ Mehrdad Farzandipour, Ehsan Nabovati, Soheila Saeedi, Esmaeil Fakharian. Fuzzy decision support systems to diagnose musculoskeletal disorders: A systematic literature review . Comput Methods Programs Biomed. 2018 Sep;163:101-109. doi: 10.1016/j.cmpb.2018.06.002. Epub 2018 Jun 6.
- ↑ Long Huang, Shaohua Xu, Kun Liu, Ruiping Yang, Lu Wu. A Fuzzy Radial Basis Adaptive Inference Network and Its Application to Time-Varying Signal Classification . Comput Intell Neurosci, 2021 Jun 23;2021:5528291.
doi: 10.1155/2021/5528291.eCollection 2021. - ↑ Mehrbakhsh Nilashi, Othman Ibrahim, Ali Ahani. Accuracy Improvement for Predicting Parkinson's Disease Progression. Sci Rep. 2016 Sep 30;6:34181. doi: 10.1038/srep34181.
particularly focusing on the field of the neurophysiology of the masticatory system