Conclusione della sezione “Scienza Normale”.
Conclusione della sezione “Scienza Normale”.
Article by Gianni Frisardi · Giorgio Cruccu · Luca Fontana · Cesare Iani · Diego Centonze · Manuel Luci · Flavio Frisardi
|
Introduzione
Abbiamo raggiunto la conclusione della sezione sulla 'Scienza Normale', che equivale fondamentalmente alla fase 2 dei 'Paradigmi di Kuhn', dove è stato presentato lo status quo del paradigma nel campo del Dolore Orofacciale (OP) e dei Disordini Temporomandibolari (TMD). Allo stesso tempo, sono stati evidenziati una serie di problemi diagnostici che non sono ancora classificabili come 'Anomalie' ma piuttosto come elementi critici da valutare nel contesto del capitolo.
Le condizioni croniche di 'OP' possono essere particolarmente difficili da diagnosticare e trattare a causa della loro complessità e della limitata comprensione dei meccanismi alla base della loro eziologia e patogenesi.[1][2] Una caratteristica frequente dell' 'OP' è la natura multifattoriale della patologia, che complica ulteriormente la diagnosi. I TMD, ad esempio, noti come Disordini Temporo-Mandibolari (TMD), Dolore Cranio-Facciale (CFP) e Disfunzione dell'Articolazione Temporo-Mandibolare (disfunzione TMJ) nei paesi anglosassoni, a volte presentano sfide diagnostiche. Il dolore orofacciale causato dai TMD spesso si sovrappone a sintomi e segni clinici simili ad altri disturbi dolorosi, che possono essere manifestazioni di altre malattie neurologiche sistemiche. Questo scenario clinico può rendere difficile la diagnosi differenziale, specialmente nelle fasi iniziali della malattia.[3][4][5][6] In una percentuale di pazienti con disturbi funzionali dell'apparato stomatognatico, sono stati identificati alcuni fattori di rischio periferici, cioè occlusali[7][8][9][10][11][12] così come una serie di fattori di rischio biopsicosociali centrali riguardanti le disfunzioni del Sistema Nervoso Centrale.[13][14][15] Tuttavia, questi studi non hanno fornito nuove informazioni sulle cause principali dei TMD e sulle loro implicazioni per la gestione di questi pazienti[16] e di conseguenza, sono stati proposti una vasta gamma di trattamenti per lo più conservativi[17][18][19][20] ma la mancanza di evidenze cliniche ha permesso di contestare il ruolo dell'occlusione nei TMD[21] sebbene non vi siano prove scientifiche che contraddicano un ruolo causale dell'occlusione nei disturbi funzionali.[22][23]
In conclusione, un ostacolo critico nella comprensione dei TMD e quindi nella diagnosi differenziale con 'OP' è stata la perdita di criteri diagnostici standardizzati per definire i sottotipi di TMD, e per questo motivo sono stati condotti numerosi studi per creare un metodo di valutazione diagnostica standardizzata chiamato Research Diagnostic Criteria (RDC) e firmato in RDC. Per ulteriori informazioni sul tema RDC segui il capitolo specifico.
Il fatto è che nei capitoli precedenti abbiamo evidenziato questioni critiche da non sottovalutare sia per il ritardo nella diagnosi sia per il pericolo di errori diagnostici che possono compromettere la salute dei pazienti, come ben documentato nella presentazione dei casi clinici. Lo studio clinico prospettico, che presenteremo in questo capitolo, costituirà la base di un nuovo paradigma diagnostico che vedremo realizzato alla fine della stesura editoriale di Masticationpedia e precisamente nella sezione 'Scienza Straordinaria'. Data la complessità, delicatezza e criticità del tema, lo studio clinico prospettico è durato 5 anni durante i quali i soggetti coinvolti sono stati studiati, seguiti e riesaminati in tre tempi diversi: in un momento Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_0=} Fase diagnostica preliminare; un tempo Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_n=} Fase diagnostica avanzata e infine un tempo Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_{n+1}=} Fase diagnostica definitiva che chiuderà il progetto da cui sarà modellato un protocollo chiamato 'Indice Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\Psi\rangle} ', letto come 'Indice ket Psi'.
L'accuratezza dei dati derivati dallo studio prospettico in vari tempi di valutazione è stata correlata con il modello bayesiano, motivo per cui è necessario richiamarlo brevemente.
Teorema di Bayes
Il teorema di Bayes è un principio importante della teoria della probabilità che ci permette di aggiornare le credenze o le probabilità su un evento alla luce di nuove evidenze o informazioni. In altre parole, ci consente di ricalcolare la probabilità di un'ipotesi, data l'osservazione di alcuni dati.
La formula per il teorema di Bayes è:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)}}
dove:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(A|B)} - Probabilità che A si verifichi dopo aver osservato B,
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(B|A)} - Probabilità di osservare B se A è vero,
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(A)} - Probabilità iniziale di A,
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(B)} - Probabilità totale.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(B)} è cruciale per comprendere la discussione che segue. Viene spesso chiamata la 'Formula della Probabilità Totale'.
In termini semplici, il teorema di Bayes ci dice come aggiornare la nostra credenza su un'ipotesi (evento A) alla luce di nuove evidenze (evento B). Praticamente, può essere utile quando abbiamo una conoscenza preliminare sulla probabilità di un evento Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(A)} e otteniamo nuove informazioni che potrebbero influenzare questa probabilità Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(B|A)} . Il teorema di Bayes ci consente di calcolare la probabilità aggiornata dell'evento Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} alla luce di queste nuove informazioni. Un esempio comune è il test diagnostico in medicina. Supponiamo di avere una malattia rara, con una probabilità dell'1% di colpire la popolazione. Il test per questa malattia ha una sensibilità dell'80% e una specificità del 90%. Se otteniamo un risultato positivo al test, come dovremmo interpretarlo?
Utilizzando il teorema di Bayes, possiamo calcolare la probabilità che una persona abbia effettivamente la malattia data la positività del test. Ciò comporta il calcolo delle probabilità condizionate della malattia data un risultato positivo al test, utilizzando le informazioni sulla sensibilità e specificità del test insieme alla prevalenza della malattia nella popolazione.
In breve, il teorema di Bayes fornisce un modo potente per aggiornare le nostre credenze o probabilità basate su nuove evidenze o informazioni, rendendolo uno strumento fondamentale in molti campi, dalla statistica alla medicina, all'intelligenza artificiale.
A questo punto, possiamo trasferire i risultati del test RDC in Bayes e quantificare le probabilità di positività e/o negatività clinica. Iniziamo con i dati derivanti dalla prima analisi del campione basata sul modello RDC classico e chiamata Indice Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi} al tempo Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_0} .

Indice Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi} al tempo Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_0}
Iniziamo con una panoramica dei risultati ottenuti dal modello RDC applicato a un campione di 30 soggetti asintomatici e 10 sintomatici, analizzando la sensibilità e la specificità del test e, di conseguenza, la probabilità totale calcolata tramite il teorema di Bayes. Questo teorema è fondamentale per valutare la probabilità che un paziente con un test positivo sia effettivamente affetto dalla malattia.
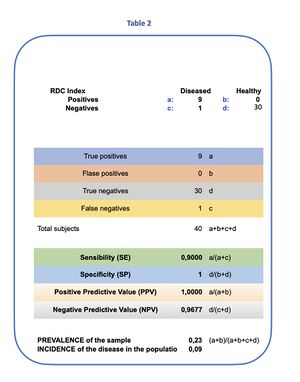
Il modello ha identificato 9 soggetti sintomatici affetti da TMD che soddisfavano i criteri clinici RDC e un soggetto sano tra i sintomatici, con una prevalenza della malattia del 9%[24] nella popolazione esaminata. (Tabella 1) Procediamo ora ad applicare il teorema di Bayes ai dati statistici.
Basandoci sui risultati del test RDC per i nostri 40 soggetti, di cui 9 sono stati considerati affetti da TMD e 1 come falso negativo, procediamo come segue:
- Prevalenza (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(A)} ): 9%,
- Sensibilità (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(B|A)} ): 90%,
- Specificità (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(\neg B|\neg A)} ): 100%, quindi Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(B|\neg A) = 0} .
Calcolo della Formula della Probabilità Totale Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(B)}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(B) = P(B|A) \cdot P(A) + P(B|\neg A) \cdot (1 - P(A)) = 0.081}
Questo calcolo è essenziale per affrontare i concetti che seguiranno.
Calcolo di Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(A|B)}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(A|B) = \frac{0.90 \cdot 0.09}{0.081} = 1.00}
Pertanto, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(A|B)} rappresenta la probabilità che il paziente sia affetto da TMD dato che il risultato del test è positivo. Questo risultato, che indica una certezza del 100% nella diagnosi dopo un test RDC positivo per i TMD, solleva preoccupazioni sul valore elevato di certezza probabilistica e sulla possibile presenza di altre patologie gravi che potrebbero manifestare sintomi simili ai TMD in una fase iniziale.
Martina K. Shephard e Gary Heir[25] illustrano nel loro articolo scientifico che varie condizioni patologiche possono confondere la diagnosi di Dolore Orofacciale, come i TMD, includendo malattie cardiovascolari, disturbi muscoloscheletrici e condizioni neurologiche.
Per questo motivo, abbiamo sottoposto i soggetti sintomatici a ulteriori valutazioni da parte di un team multidisciplinare. Il follow-up, conclusosi dopo due anni, ha fornito risposte significative ai dubbi espressi, dimostrando la complessità delle diagnosi mediche e l'importanza di un approccio olistico nella valutazione dei sintomi. Infatti, i dati aggiornati sono stati ricalcolati contemporaneamente a una serie di impostazioni statistiche alternative. Questo secondo passaggio è stato chiamato, appropriatamente, 'Indice Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi} ' al tempo Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_n}
Indice Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi} al tempo Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_n}
Il follow-up di due anni ha rivelato che molti dei 10 soggetti sintomatici erano affetti da gravi malattie neurologiche e sistemiche, come meningiomi, cavernomi pineali, sclerodermia e spasmi emimasticatori. Queste condizioni sono già state descritte nei capitoli della sezione "Scienza Normale". La scoperta di tali gravi patologie tra i soggetti esaminati ha suscitato notevole preoccupazione, rivelando un alto rischio per la vita di alcuni individui. Questo risultato deve essere interpretato come un'anomalia epistemologica che trascende i dogmi delle scuole di pensiero consolidate.
La mentalità prevalente in medicina è basata su un formalismo deterministico, secondo cui variabili, eventi e dati sono commutabili, e invertire i dati di output non altera il risultato. Tuttavia, nella pratica clinica, emerge una variabile critica: il tempo. Il tempo stabilisce un ordine sia nella manifestazione del danno organico sia nei sintomi di dolore orofacciale e/o bruxismo. Questa considerazione, apparentemente logica e banale, introduce una questione epistemologica profonda, in quanto segna il passaggio da un modello statistico classico e deterministico a un modello quantistico e indeterminato.
Consideriamo il caso clinico di un paziente affetto da bruxismo, descritto nel capitolo "Bruxismo". Il paziente ha riferito bruxismo notturno e diurno già dal 2000 ai suoi colleghi odontoiatri, che sono intervenuti con il trattamento del biteplane. In quel contesto, la diagnosi era di TMD, formulata attraverso il modello RDC già nel 2000. I colleghi hanno continuato a seguire il paziente fino al 2014, anno in cui si è presentato al nostro Centro di Neurognatologia. Durante la prima fase della ricerca sperimentale, chiamata "Indice Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi} al tempo Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_0} ", la diagnosi di bruxismo, secondo il modello RDC, è stata confermata poiché il paziente soddisfaceva i requisiti specifici del modello. Tuttavia, successivamente, al tempo Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_n} (come descritto in precedenza), la diagnosi è cambiata in "Cavernoma Pineale".
Supponiamo che nel 2000 i colleghi odontoiatri avessero eseguito un'EMG interferenziale dei masseteri (Figura 1) e, non rilevando anomalie neuromotorie (simmetria delle ampiezze e frequenza di scarica delle unità motorie), avessero concluso, naturalmente, che il paziente fosse sano nonostante episodi sporadici di bruxismo. Tuttavia, con l'intervento del 2014, quando abbiamo eseguito il Ciclo di Recupero del Riflesso Inibitorio del Massetere (Figura 2), abbiamo rivelato una grave ipereccitabilità neuromotoria trigeminale organica, portando alla diagnosi definitiva di "Cavernoma Pineale". Questo dimostra come, già dal 2000, il danno organico potesse essere presente ma la diagnosi è cambiata solo nel 2014, illustrando l'importanza dell'ordine delle informazioni e la non commutabilità dei dati.
In questa esplorazione, senza entrare in dettagli eccessivamente tecnici, introduciamo il concetto di variabili non commutative e il loro impatto sulla pratica medica.
Variabili non commutative
Modello di Bayes
Come accennato in precedenza, il modello di Bayes serve ad aggiornare le probabilità di diagnosi alla luce di nuove evidenze. Riportiamo il formalismo matematico per seguire meglio le differenze tra i modelli:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)}} e solo il termine Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(B)} che è cruciale per comprendere la discussione che segue. Questo, lo ripetiamo, è spesso chiamato la 'Formula della Probabilità Totale'.
Modello Quantistico
Il modello quantistico impiega operatori matematici che possono essere non commutativi, dimostrando come l'ordine di applicazione degli operatori possa influenzare il risultato.
Infatti, la proprietà:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{A}\hat{B} \neq \hat{B}\hat{A}}
non trova un analogo diretto nel modello bayesiano, che non considera l'effetto dell'ordine dei test.
A differenza dei modelli classici, i modelli quantistici possono incorporare effetti di sovrapposizione e interferenza tra stati, che sono assenti nella teoria della probabilità classica.
Limiti del Modello di Bayes
Il modello di Bayes non tiene conto dell'ordine dei test; semplicemente somma le evidenze senza considerare come l'ordine possa influenzare i risultati. Le probabilità nel modello di Bayes sono interpretate come misure di incertezza basate sulle informazioni disponibili, mentre nella meccanica quantistica, le probabilità emergono anche dai principi di sovrapposizione e non-località. Per distinguerlo dal noto Teorema di Bayes ma al contempo differenziarlo dai modelli di tipo quantistico, potremmo chiamare questo approccio 'QBism'.
Quantum Bayesianism ‘QBism’
I modelli non classici come Bayes forniscono una prospettiva basata sui principi della meccanica quantistica, illustrando come l'ordine dei test diagnostici possa influenzare i risultati della diagnosi, sfruttando la non commutatività degli operatori quantistici.
Non commutatività dei Dati
Ogni test diagnostico è modellato come un operatore quantistico che agisce su uno spazio di stato, rappresentando le diverse condizioni di salute del paziente.
- Operatore EMG Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{E}}
(vedi figura 1)
- Poco efficace per rilevare l'ipereccitabilità neuromotoria trigeminale.
- Matrice dell'operatore:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{E} = \begin{pmatrix} 0.95 & 0.05 \\ 0.05 & 0.95 \end{pmatrix}}
- Operatore rcIMR Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{P}}
(vedi figura 2)
- Molto efficace per rilevare l'ipereccitabilità neuromotoria trigeminale.
- Matrice dell'operatore:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{P} = \begin{pmatrix} 0.1 & 0.9 \\ 0.9 & 0.1 \end{pmatrix}}
Stato Iniziale del Paziente
- Il vettore di stato iniziale del paziente è:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi=\begin{pmatrix} 1 \\ 0 \end{pmatrix}} Questo indica che il paziente è inizialmente considerato sano.
Simulazione dei Risultati
- Scenario 1: EMG nel 2000 seguito dal test rcIMR nel 2014
- Risultato dopo l'EMG:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{E} \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \begin{pmatrix} 0.95 \\ 0.05 \end{pmatrix}}
Questo indica che, dopo l'applicazione dell'EMG, il vettore di stato mostra una probabilità del 95% che il paziente sia sano e solo una probabilità del 5% di malattia, evidenziando la scarsa sensibilità dell'EMG per la patologia in questione (Cavernoma Pineale).
- Risultato dopo rcIMR nel 2014:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{P} \begin{pmatrix} 0.95 \\ 0.05 \end{pmatrix} = \begin{pmatrix} 0.14 \\ 0.86 \end{pmatrix}}
- Questo conferma che, numericamente, l'applicazione della matrice ha trasformato lo stato in modo che la probabilità di rilevare la malattia sia aumentata significativamente (dal 5% all'86%), evidenziando la malattia che l'EMG non aveva rilevato.
- Scenario 2: rcIMR eseguito nel 2000
- Risultato immediato:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{P} \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \begin{pmatrix} 0.1 \\ 0.9 \end{pmatrix}} Avrebbe rivelato la malattia già nel 2000.
La simulazione mostra chiaramente che l'uso del test 'Ciclo di Recupero del Riflesso Inibitorio del Massetere' (rcIMR) come test iniziale nel 2000 avrebbe potuto rivelare il Cavernoma Pineale immediatamente, offrendo la possibilità di una diagnosi e un intervento 14 anni prima. Questo sottolinea l'importanza critica dell'ordine in cui vengono eseguiti i test diagnostici e l'impatto potenziale sulla gestione del paziente. La non commutatività degli operatori (test diagnostici) in medicina può avere implicazioni reali e significative per la diagnosi e il trattamento delle condizioni mediche.
Probabilità Classica vs Probabilità Quantistica
La probabilità classica (CP) è un modello formalizzato matematicamente da Kolmogorov nel 1933[26] ed è basata sul calcolo delle misure di probabilità, dove a ciascun evento viene assegnato un peso non negativo Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p(A)} . La caratteristica fondamentale della CP è la sua additività: se due eventi Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} e Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta} sono disgiunti, la probabilità della loro unione è uguale alla somma delle loro probabilità individuali:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(\alpha \cup \beta) = P(\alpha) + P(\beta)}
Nella CP, la formula della probabilità totale (FTP) è derivata utilizzando l'additività della probabilità e la formula di Bayes, per definire la probabilità condizionata:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(B = \beta) = \sum_\alpha P(A = \alpha) P(B = \beta \mid A = \alpha)}
La probabilità quantistica (QP), invece, opera con ampiezze di probabilità complesse piuttosto che semplici misure di probabilità. La QP è considerata un modello vettoriale di ragionamento probabilistico, dove ciascuna ampiezza complessa determina la probabilità secondo la regola di Born:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P = |\psi|^2} , dove Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\psi|^2} è il quadrato del modulo dell'ampiezza complessa.
A differenza della CP, la QP consente la violazione delle leggi fondamentali della CP a causa delle ampiezze di probabilità complesse.
Nella QP, la versione classica della FTP è modificata dal termine di interferenza. Per gli osservabili quantistici Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} e Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B} , rappresentati da operatori hermitiani Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{A}} e Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{B}} , la versione quantistica della FTP appare come segue (la formula è stata divisa in due parti per motivi di spazio e descrizione):
| Parte 1: | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \longrightarrow} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(B = \beta) = \sum_\alpha P(A = \alpha_1) P(B = \beta \mid A = \alpha_1) } | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Eq.1} | |||||||
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle + } | ||||||||||
| Parte 2: | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \longrightarrow} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2\sum_{\alpha_1 < \alpha_2} \cos\theta_{\alpha_1 \alpha_2} \sqrt{P(A = \alpha_1) P(B = \beta \mid A = \alpha_1) P(A = \alpha_2) P(B = \beta \mid A = \alpha_2)}} | ||||||||
Questa equazione evidenzia come la QP differisca significativamente dalla CP, soprattutto nella modulazione indotta dall'interferenza dei dati, offrendo una nuova prospettiva su come l'ordine dei test diagnostici possa influenzare i risultati.
Dati derivati dal follow-up al tempo Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_n}
Consideriamo una vista clinica più pratica di ciò che accade ai nostri cari dati che escono dalla tabella:
- Popolazione Totale: 40 individui
- Totale Sintomatici: 10 individui
- Con TMD effettivi: 9 (numero di soggetti sintomatici diagnosticati dal modello RDC)
- Con Altre Patologie Gravi (non-TMD): 7 (durante il follow-up al tempo Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_n} da parte del gruppo di esperti, è stato verificato che tra i 10 soggetti sintomatici, 7 erano affetti da gravi patologie non-TMD)
- Falso Negativo (malato ma considerato sano): 1 (tra i 10 soggetti sani rimasti come falso negativo sia nel test RDC che nella verifica del gruppo di esperti al tempo Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_n} il solito soggetto N° 40)
Dati di test dalla tabella 2 che rappresentano l'analisi statistica e Bayes al tempo Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_0} abbiamo:
- Sensibilità (SE): Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 90%\longrightarrow 0.9}
- Specificità (SP): Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 100%\longrightarrow1}
- Prevalenza dei TMD tra i Sintomatici: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(A=\alpha_1) = \frac{9}{10} = 0.9} . Questo indica che 9 su 10 individui sintomatici sono stati diagnosticati come TMD tramite il modello RDC. Questo corrisponde a una prevalenza del Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 90%\longrightarrow 0.9} in termini matematici, nel gruppo dei sintomatici. Questo calcolo riflette correttamente la proporzione di soggetti affetti da TMD rispetto al numero totale di sintomatici
- Probabilità dei TMD: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(B = \beta \mid A = \alpha_1) = 0.9} — Probabilità di essere diagnosticati correttamente come TMD se si ha un TMD (alta sensibilità del test).
- Prevalenza di Altre Patologie Gravi tra i Sintomatici: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(A=\alpha_2) = \frac{7}{10} = 0.7} . Questo indica che 7 su 10 individui sintomatici sono stati identificati con patologie gravi diverse dai TMD durante il follow-up al tempo Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_n} . Questo rappresenta una prevalenza del Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 70%\longrightarrow0.7} in termini matematici, nel gruppo di sintomatici classificati come non-TMD.
- Probabilità di non-TMD: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(B = \beta \mid A = \alpha_2)} — Probabilità di essere erroneamente diagnosticati come TMD quando si ha una patologia non-TMD
- Angolo Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta = \frac{\pi}{1.5}} : L'angolo Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta } assume un'importanza significativa in questo contesto, cioè una differenza tra i dati che escono dall'esperimento tra i soggetti classificati come pazienti affetti da TMD tramite il test RDC (quantità 9 su 10) e quelli diagnosticati al tempo Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_n} dal gruppo di esperti considerati malati con gravi patologie non-TMD (7 su 10). Questo rapporto è quindi quantificato come Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\pi}{1.5}} in radianti che, convertito in gradi, corrisponde a un angolo Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta =120^\circ } . L'angolo Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta} rappresenta un concetto matematico che in questo contesto specifico viene utilizzato per quantificare la discrepanza tra due categorie diagnostiche all'interno dello stesso gruppo di pazienti sintomatici: pazienti con TMD e quelli con altre patologie gravi (non-TMD). La scelta di rappresentare questa discrepanza attraverso un angolo e il suo coseno può essere vista come un tentativo di applicare principi di geometria o fisica (come l'interferenza delle onde) per interpretare la complessità delle diagnosi mediche. Ecco come questo concetto può influenzare la pratica clinica:
- Differenziazione Diagnostica: L'angolo Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta = 120^\circ} e il valore del coseno di Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta} (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -0.5} ) indicano una separazione distinta tra i due gruppi diagnostici nel contesto del modello di analisi. Un angolo di 120°, che è relativamente ampio, suggerisce che le caratteristiche dei pazienti con TMD sono sostanzialmente diverse da quelle dei pazienti con altre patologie gravi. Questo può aiutare i clinici a considerare l'importanza di non sovrapporre trattamenti e affinare gli strumenti diagnostici per mirare meglio le terapie.
- Implicazioni per Diagnosi e Trattamento: L'interpretazione dell'angolo e del coseno può essere utilizzata per valutare quanto bene un test diagnostico distingue tra queste due condizioni. Se il coseno fosse vicino a 1 (o Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta} vicino a 0°), indicherebbe che i test non stanno facendo una buona distinzione tra le condizioni. Al contrario, un valore di coseno negativo indica una distinzione marcata, che è cruciale per evitare trattamenti inappropriati o inefficaci.
- Sviluppo di Protocolli Specifici: Comprendere la natura di Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta} può portare allo sviluppo di protocolli diagnostici e terapeutici più specializzati, migliorando l'efficacia del trattamento per ciascun gruppo di patologie. Questo approccio è particolarmente rilevante nel campo medico dove la precisione della diagnosi influisce direttamente sul successo del trattamento.
- Coseno dell'angolo Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta\longrightarrow } Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cos(\theta) = -0.5} : Pertanto, possiamo interpretare Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta =120^\circ } come l'angolo che rappresenta questa proporzione, il cui Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cos(\theta) = -0.5} . In questo contesto, il coseno di Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta } può essere considerato come una misura della discrepanza tra Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_1 } e Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_2 } , dove valori più alti di Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cos\theta } indicano una maggiore differenza tra soggetti sintomatici malati di TMD e quelli non-TMD
Calcolo della Probabilità di un Vero Positivo
La probabilità di un vero positivo nel test RDC e quindi affetto da TMD senza considerare l'interferenza con altre patologie diagnosticate al tempo Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_n} è calcolata come:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(B=\text{TMDs} | A=\alpha_1) = 0.9 \times 0.9 = 0.81\longrightarrow 81%} e per seguire il concetto di probabilità quantistica più agevolmente nell'equazione 1, la prima parte dell'equazione sarà completata come segue:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(B = \beta) = \sum_\alpha P(A = \alpha_1) P(B = \beta \mid A = \alpha_1 ) \longrightarrow P(B=\text{TMDs} | A=\alpha_1) = 0.9 \times 0.9 = 0.81\longrightarrow 81% }
Calcolo dell'Interferenza
L'interferenza è calcolata utilizzando la formula:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Interference} = 2 \times \cos(\theta) \times \sqrt{P(A=\alpha_1) \times P(B=\text{TMDs} | A=\alpha_1)} \times \sqrt{P(A=\alpha_2)}\rightarrow} Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2 \times (-0.5) \times \sqrt{0.9 \times 0.81} \times \sqrt{0.7} \approx -0.7144}
L'efficacia del test, aggiustata per l'interferenza, è Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(B=\text{TMDs} | A=\alpha_{\text{TMDs}}) + \text{Interference}}
Questo risultato indica una drastica riduzione dell'efficacia del test diagnostico quando si considera l'interferenza causata dalla coesistenza di altre patologie.
Riassumiamo sinteticamente riportando la formula delle probabilità quantistiche Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Eq.1} , i dati numerici per comprendere meglio il significato delle procedure matematiche e il significato clinico diagnostico derivato come segue:
| Part 1: | Part 2: | ||||
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(B = \beta) = \sum_\alpha ( 0.9 \times 0.9) } | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle +} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2 \times (-0.5) \times \sqrt{0.9 \times 0.81} \times \sqrt{0.7} 6 % } | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Eq.2} | ||
Conclusione
La diagnosi dei Disturbi Temporomandibolari (TMD) attraverso il modello RDC e l'uso del Teorema di Bayes rappresenta un approccio robusto che integra dati clinici con principi statistici avanzati. Tuttavia, la complessità di una tale diagnosi risiede non solo nella variabilità dei sintomi ma anche nell'interferenza di altre patologie che possono imitare o aggravare i sintomi dei TMD. La specificità e la sensibilità del test diagnostico, sebbene elevate, non escludono il rischio di falsi positivi o negativi, anche quelli non rappresentati nel modello RDC, evidenziando la necessità di un approccio diagnostico più olistico e multidisciplinare.
La probabilità di un vero positivo calcolata come mostra un'alta probabilità che il paziente sia effettivamente affetto da TMD quando il test è positivo secondo il modello RDC. Tuttavia, l'introduzione dell'angolo che misura la discrepanza tra i pazienti con TMD e quelli con altre gravi patologie non-TMD condotte nel follow-up dal gruppo di esperti, sottolinea la complessità dell'utilizzo di un singolo parametro diagnostico per differenziare le varie condizioni cliniche.
L'interferenza calcolata, che riduce drasticamente l'efficacia del test a , solleva seri dubbi sulla sua utilità senza un'adeguata considerazione delle condizioni concomitanti. Questo sottolinea l'importanza di un follow-up dettagliato e di una valutazione clinica che non si basi esclusivamente su risultati quantitativi.
Il modello di Bayes, sebbene sia uno strumento potente nella riformulazione delle probabilità diagnostiche, mostra i suoi limiti nel campo dei TMD a causa della complessa eziologia e presentazione clinica di questi disturbi. La discussione sul modello quantistico, che considera la non commutatività dei dati, apre nuove prospettive sulla gestione dei dati diagnostici, suggerendo che l'ordine in cui vengono eseguiti i test può alterare significativamente l'interpretazione dei risultati. Questo modello offre un approccio innovativo che potrebbe migliorare l'accuratezza diagnostica, specialmente in scenari clinici complessi dove molteplici interazioni tra vari test e sintomi possono alterare le probabilità diagnostiche.
In futuro, integrare modelli quantistici insieme ai metodi diagnostici consolidati potrebbe non solo affinare le nostre capacità diagnostiche per i TMD, ma anche offrire una comprensione più profonda delle interdipendenze tra vari sintomi e condizioni. Ciò richiederebbe ulteriori studi e validazioni per garantire che tali metodi non siano solo teoricamente validi ma anche praticamente applicabili nel contesto clinico.
In sintesi, mentre il modello di Bayes continua a essere un pilastro fondamentale nell'analisi probabilistica in medicina, l'adozione di approcci basati sulla meccanica quantistica potrebbe rivoluzionare il modo in cui comprendiamo e gestiamo malattie complesse come i TMD. Questo sottolinea l'importanza di un approccio diagnostico che sia al contempo rigoroso e flessibile, capace di adattarsi e integrare nuove scoperte scientifiche e tecnologiche.
- ↑ NASEM Temporomandibular Disorders: Priorities for Research and Care The National Academies Press, Washington, DC (2020), 10.17226/25652
- ↑ B.J. Sessle. Chronic orofacial pain: models, mechanisms, and genetic and related environmental influences. Int J. Mol. Sci., 22 (2021), p. 7112, 10.3390/ijms22137112
- ↑ Sollecito T.P., Richardson R.M., Quinn P.D., Cohen G.S.: Intracranial schwannoma as atypical facial pain. Case report. Oral Surg Oral Med Oral Pathol. 1993;76:153-6
- ↑ Shankland W.E.: Trigeminal neuralgia: typical or atypical? Cranio. 1993;11:108-12.
- ↑ Graff-Radford S.B., Solberg W.K.: Is atypical odontalgia a psychological problem? Oral Surg Oral Med Oral Pathol. 1993;75:579-82.
- ↑ Ruelle A., Datti R., Andrioli G.: Cerebellopontine angle osteoma causing trigeminal neuralgia: case report. Neurosurgery. 1994;35:1135-7.
- ↑ B.C. Cooper Temporomandibular disorders: a position paper of the International College of Cranio-Mandibular Orthopedics (ICCMO) Cranio, 29 (2011), pp. 237-244, 10.1179/crn.2011.034
- ↑ M.S. Nguyen, T. Jagomägi, T. Nguyen, M.Saag, Ü. Voog-Oras Occlusal support and temporomandibular disorders among elderly Vietnamese Int J. Prosthodont, 30 (2017), pp. 465-470, 10.11607/ijp.5216
- ↑ M.S. Nguyen, M. Saag, T. Jagomägi, Q.H.Nguyen, Ü. Voog-Oras The impact of occlusal support on temporomandibular disorders: a literature review Proc. Singap. Healthc., 31 (2021), pp. 1-12, 10.1177/2010105821102
- ↑ T.R. Walton, D.M. Layton Mediotrusive occlusal contacts: best evidence consensus statement J. Prosthodont, 30 (S1) (2021), pp. 43-51, 10.1111/jopr.13328
- ↑ A. Kucukguven, M.D. Demiryurek, I.Vargel Temporomandibular joint innervation: anatomical study and clinical implications Ann. Anat., 240 (2022), Article 151882, 10.1016/j.aanat.2021.151882
- ↑ E. Tervahauta, L. Närhi, P. Pirttiniemi, K.Sipilä, R. Näpänkangas, M. Tolvanen, V.Vuollo, A.S. Silvola Prevalence of sagittal molar and canine relationships, asymmetries and midline shift in relation to temporomandibular disorders (TMD) in a Finnish adult population Acta Odontol. Scand., 80 (2022), pp. 1-11, 10.1080/00016357.2022.2036364
- ↑ R.B. Fillingim, R. Ohrbach, J.D.Greenspan, C. Knott, R. Dubner, E. Bair, C. Baraian, G.D. Slade, W. Maixner Potential psychosocial risk factors for chronic TMD: descriptive data and empirically identified domains from the OPPERA case-control study J. Pain., 12 (11 Suppl) (2011), pp. T46-T60, 10.1016/j.jpain.2011.08.007
- ↑ G.D. Slade, R. Ohrbachm, J.D.Greenspan, R.B. Fillingim, E. Bair, A.E.Sanders, R. Dubner, L. Diatchenko, C.B.Meloto, S. Smith, W. Maixner Painful temporomandibular disorder: decade of discovery from OPPERA studies J. Dent. Res, 95 (10) (2016), pp. 1084-1092, 10.1177/0022034516653743
- ↑ G.D. Slade, R. Ohrbach, J.D. Greenspan, R.B. Fillingim, E. Bair, A.E. Sanders, R.Dubner, L. Diatchenko, C.B. Meloto, S.Smith, W. Maixner Painful temporomandibular disorder: decade of discovery from OPPERA studies J. Dent. Res, 95 (2016), pp. 1084-1092, 10.1177/0022034516653743
- ↑ P. Svensson, F. Exposto Commentary 2: further evidence for overlaps among chronic pain conditions-but no news about causal relationships J. Oral. Facial Pain. Headache, 34(Suppl) (2020), pp. s6-s8, 10.11607/ofph.2020.suppl.c2
- ↑ C.S. Stohler, G.A. Zarb On the management of temporomandibular disorders: a plea for a low-tech, high-prudence therapeutic approach J. Orofac. Pain., 13 (1999), pp. 255-261
- ↑ J. Feng, M. Luo, J. Ma, Y. Tian, X. Han, D.Bai The treatment modalities of masticatory muscle pain a network meta-analysis Med. (Baltim. ), 98 (2019), Article e17934, 10.1097/MD.0000000000017934
- ↑ Z. Al-Ani Occlusion and temporomandibular disorders: a long-standing controversy in dentistry Prim. Dent. J., 9 (2020), pp. 43-48, 10.1177/2050168420911029
- ↑ C. Penlington, C. Bowes, G. Taylor, A.A.Otemade, P. Waterhouse, J. Durham, R.Ohrbach Psychological therapies for temporomandibular disorders (TMDs) Cochrane Database Syst. Rev., Issue 8(2022), Article CD013515, 10.1002/14651858.CD013515.pub2
- ↑ P. Alanen Occlusion and temporomandibular disorders (TMD): still unsolved question? J. Dent. Res, 81 (2002), pp. 518-519, 10.1177/154405910208100803
- ↑ P. Kirveskari, T. Jamsa, P. Alanen Occlusal adjustment and the incidence of demand for temporomandibular disorder treatment J. Prosthet. Dent., 79 (1998), pp. 433-438, 10.1016/s0022-3913(98)70158-1
- ↑ T. de Abreu, C. Bahia, T. Foscaldo, P.Senna, H. de Souza, R. Fischer, P.Kirveskari Effect of occlusal equilibration on masticatory muscle activity in females with sleep bruxism: a double-blind randomised controlled trial J. Sleep. Res., 14 (2023), Article e13879, 10.1111/jsr.13879
- ↑ ?
- ↑ Martina K. Shephard & Gary Heir.Orofacial Pain in the Medically Complex Patient. Contemporary Oral Medicine, 26 January 2019
- ↑ Kolmogorov A.N. Grundbegriffe Der Wahrscheinlichkeitsrechnung Springer-Verlag, Berlin (1933)