Difference between revisions of "Die Logik der probabilistischen Sprache"
| (4 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
{{ | {{main menu}}[[File:Spasmo_emimasticatorio_JJ.jpg|alt=|left|250x250px]] | ||
Der Text behandelt die Logik der probabilistischen Sprache im medizinischen Bereich und hebt hervor, wie Unsicherheit ein wesentlicher Bestandteil wissenschaftlicher Praxis ist. Durch probabilistische und statistische Konzepte wird versucht, die mit medizinischer Theorie und Praxis verbundenen Unsicherheiten zu bewältigen und zu verstehen. | |||
Die Rolle der Wahrscheinlichkeit im Verhältnis zwischen Theorie und Beobachtung wird betont, wobei zwischen subjektiver Unsicherheit und Zufälligkeit unterschieden wird. Subjektive Unsicherheit betrifft den Wissens- und Überzeugungsstand der Individuen, während Zufälligkeit auf das Fehlen einer bestimmten Verbindung zwischen Ursache und Wirkung verweist. | |||
Im medizinischen Ansatz wird die Bedeutung des Verständnisses und der Unterscheidung zwischen subjektiver und objektiver Wahrscheinlichkeit erörtert. Subjektive Wahrscheinlichkeit spiegelt den individuellen Glauben wider, während objektive Wahrscheinlichkeit auf Daten und empirischen Beweisen beruht. | |||
Das Konzept der probabilistisch-kausalen Analyse wird dann weiter vertieft, das darauf abzielt, die Beziehung zwischen Ereignissen und zufälligen Prozessen bei der klinischen Diagnose zu quantifizieren. Es wird eine detaillierte Darstellung darüber gegeben, wie bedingte Wahrscheinlichkeiten interpretiert und wie die Aufteilung der kausalen Relevanz genutzt werden kann, um eine Differentialdiagnose zu formulieren. | |||
Schließlich wird das Thema der Interdisziplinarität in der wissenschaftlichen Forschung angesprochen, wobei die Bedeutung eines interdisziplinären Ansatzes zur Bewältigung komplexer Probleme hervorgehoben wird. Auch die Fuzzylogik wird als mögliches Instrument zur Bewältigung von Unsicherheiten in medizinischen Kontexten erwähnt. | |||
{{ArtBy| | {{ArtBy| | ||
| Line 24: | Line 15: | ||
| autore2 = Riccardo Azzali | | autore2 = Riccardo Azzali | ||
| autore3 = Flavio Frisardi | | autore3 = Flavio Frisardi | ||
}} | }}{{:Store:LPLde01}} | ||
{{:Store: | |||
{{:Store: | {{:Store:LPLde02}} | ||
{{:Store: | {{:Store:LPLde03}} | ||
{{:Store: | {{:Store:LPLde04}} | ||
{{:Store: | {{:Store:LPLde05}} | ||
Latest revision as of 09:57, 20 October 2024
Die Logik der probabilistischen Sprache
Der Text behandelt die Logik der probabilistischen Sprache im medizinischen Bereich und hebt hervor, wie Unsicherheit ein wesentlicher Bestandteil wissenschaftlicher Praxis ist. Durch probabilistische und statistische Konzepte wird versucht, die mit medizinischer Theorie und Praxis verbundenen Unsicherheiten zu bewältigen und zu verstehen.
Die Rolle der Wahrscheinlichkeit im Verhältnis zwischen Theorie und Beobachtung wird betont, wobei zwischen subjektiver Unsicherheit und Zufälligkeit unterschieden wird. Subjektive Unsicherheit betrifft den Wissens- und Überzeugungsstand der Individuen, während Zufälligkeit auf das Fehlen einer bestimmten Verbindung zwischen Ursache und Wirkung verweist.
Im medizinischen Ansatz wird die Bedeutung des Verständnisses und der Unterscheidung zwischen subjektiver und objektiver Wahrscheinlichkeit erörtert. Subjektive Wahrscheinlichkeit spiegelt den individuellen Glauben wider, während objektive Wahrscheinlichkeit auf Daten und empirischen Beweisen beruht.
Das Konzept der probabilistisch-kausalen Analyse wird dann weiter vertieft, das darauf abzielt, die Beziehung zwischen Ereignissen und zufälligen Prozessen bei der klinischen Diagnose zu quantifizieren. Es wird eine detaillierte Darstellung darüber gegeben, wie bedingte Wahrscheinlichkeiten interpretiert und wie die Aufteilung der kausalen Relevanz genutzt werden kann, um eine Differentialdiagnose zu formulieren.
Schließlich wird das Thema der Interdisziplinarität in der wissenschaftlichen Forschung angesprochen, wobei die Bedeutung eines interdisziplinären Ansatzes zur Bewältigung komplexer Probleme hervorgehoben wird. Auch die Fuzzylogik wird als mögliches Instrument zur Bewältigung von Unsicherheiten in medizinischen Kontexten erwähnt.
==Probabilistische Sprachlogik in der Medizin==
Jede wissenschaftliche Idee (ob in Medizin, Architektur, Ingenieurwesen, Chemie oder einem anderen Fach) ist bei der Umsetzung in die Praxis mit kleinen Fehlern und Unsicherheiten behaftet. Mathematik – durch Wahrscheinlichkeitstheorie und statistische Inferenz – hilft, diese Unsicherheiten genau zu kontrollieren und dadurch einzudämmen. Dabei ist immer zu berücksichtigen, dass in allen praktischen Fällen "die Ergebnisse auch von vielen anderen Faktoren außerhalb der Theorie abhängen", seien es Ausgangs- und Umgebungsbedingungen, Versuchsfehler oder anderes.
All die Unsicherheiten in Bezug auf diese Faktoren machen die Theorie-Beobachtungs-Beziehung zu einer probabilistischen. Im medizinischen Ansatz gibt es zwei Arten von Unsicherheit, die Diagnosen am stärksten belasten: subjektive Unsicherheit und Zufall.[1][2]Es ist daher in diesem Szenario wesentlich, zwischen diesen beiden Unsicherheiten zu unterscheiden und zu zeigen, dass der Begriff der Wahrscheinlichkeit in diesen beiden Kontexten unterschiedliche Bedeutungen hat. Wir werden versuchen, diese Konzepte offenzulegen, indem wir jeden entscheidenden Schritt mit dem klinischen Ansatz verknüpfen, über den in den vorangegangenen Kapiteln berichtet wurde, und insbesondere mit dem Ansatz im zahnärztlichen und neurologischen Kontext im Kampf um den Vorrang der Diagnose für unsere liebe Mary Poppins.
Subjektive Unsicherheit und Unfall
Stellen wir uns vor, Mary Poppins zu fragen, welcher der beiden ärztlichen Kollegen – der Zahnarzt oder der Neurologe – Recht hat. Die Frage würde eine Art Aufregung erzeugen, die auf innerer Unsicherheit beruht; Daher beziehen sich die Begriffe Gewissheit und Ungewissheit auf subjektive epistemische Zustände von Menschen und nicht auf Zustände der Außenwelt, weil es in dieser Welt keine Gewissheit oder Ungewissheit gibt. In diesem Sinne gibt es, wie wir bereits erwähnt haben, eine innere Welt und eine Welt außerhalb von uns selbst, die beide nicht auf Kanons der Unsicherheit, sondern der Wahrscheinlichkeit reagieren. Mary Poppins kann subjektiv sicher oder unsicher sein, ob sie an TMDs oder einer neuropathischen oder neuromuskulären Form von OP leidet: Dies liegt daran, dass „Unsicherheit“ ein subjektiver, erkenntnistheoretischer Zustand unterhalb der Schwelle von Wissen und Überzeugung ist; daher der Begriff.
Subjektive Unsicherheit
Zweifellos macht der Begriff „subjektiv“ vielen Angst, insbesondere denen, die beabsichtigen, Wissenschaft zu betreiben, indem sie das gesunde Ideal der „Objektivität“ verfolgen, da dieser Begriff vom gesunden Menschenverstand wahrgenommen wird. Es ist daher angebracht, einige Erläuterungen zur Verwendung dieses Begriffs in diesem Zusammenhang zu machen:
- „Subjektiv“ gibt an, dass die Wahrscheinlichkeitsbewertung vom Informationsstand der Person abhängt, die sie durchführt.
- „Subjektiv“ bedeutet nicht willkürlich.
Die sogenannte „Objektivität“, wie sie außerhalb der wissenschaftlichen Forschung wahrgenommen wird, ist definiert, wenn eine Gemeinschaft rationaler Wesen den gleichen Informationsstand teilt. Aber selbst in diesem Fall sollte man richtiger von „Intersubjektivität“ sprechen (d. h. dem Teilen subjektiver Meinungen durch eine Gruppe).
In klinischen Fällen – gerade weil Patienten selten fortgeschrittene medizinische Vorstellungen haben – muss mit subjektiver Unsicherheit gerechnet werden. Das Leben mit Ungewissheit erfordert, dass wir einen probabilistischen Ansatz verwenden.
Lässigkeit
Die Zufälligkeit weist auf das Fehlen eines bestimmten Zusammenhangs zwischen Ursache und Wirkung hin. Die Ungewissheit einer engen Verbindung zwischen der Quelle und dem Phänomen gehört zu den nachteiligsten Problemen bei der Bestimmung einer Diagnose.
In einem klinischen Fall wird ein Phänomen (wie zum Beispiel ein Fehlbiss, ein Kreuzbiss, ein offener Biss usw.) zufällig mit einem anderen Phänomen (wie z. B. einer Degeneration des Kiefergelenks) assoziiert; Wenn es Ausnahmen gibt, für die der logische Satz nicht immer wahr ist (aber meistens), werden wir sagen, dass die Relation nicht immer wahr, aber wahrscheinlich ist.
Subjektive und objektive Wahrscheinlichkeit
In diesem Kapitel werden einige Themen behandelt, die bereits in dem fantastischen Buch von Kazem Sadegh-Zadeh behandelt wurden[3],die sich mit dem Problem der Logik medizinischer Sprache befassen, werden wieder aufgegriffen und inhaltlich umgestaltet, indem wir sie auf unseren klinischen Fall von Mary Poppins verweisen, um unser Verständnis näher an zahnärztlichen Kontexten zu halten.
Zufällige und subjektiv unsichere Ereignisse gelten als wahrscheinlich; Folglich werden Zufall und Ungewissheit als qualitative, vergleichende oder quantitative Wahrscheinlichkeiten behandelt.
Um dieses Konzept zu verdeutlichen, kehren wir zum Beispiel von Mary Poppins zurück. Ein Arzt, der ihre Symptome gehört hat, wird sagen können:
- Mary Poppins leidet wahrscheinlich an TMDs (qualitativer Begriff).
- Mary Poppins hat eher TMDs als neuropathische OP (Vergleichsbegriff: Anzahl der diagnostizierten Fälle von TMDs versus nOP.
- Die Wahrscheinlichkeit, dass Mary Poppins CMDs hat, beträgt 0,15 (quantitativer Begriff, relativ zur Bevölkerung).
Subjektive Wahrscheinlichkeit
Im Zusammenhang mit menschlicher subjektiver Unsicherheit können die probabilistischen, qualitativen, vergleichenden und/oder quantitativen Daten vom Kliniker als Maß der subjektiven Unsicherheit interpretiert werden, um die „Überzeugungszustände“ numerisch darstellbar zu machen. Zum Beispiel zu sagen, dass „die Wahrscheinlichkeit, dass Mary Poppins von TMDs betroffen ist, 0,15 der Fälle beträgt“ ist dasselbe wie zu sagen „im Maße von 15 % glaube ich, dass Mary Poppins von TMDs betroffen ist“; was bedeutet, dass der Grad der Überzeugung der Grad der subjektiven Wahrscheinlichkeit ist.
Objektive Wahrscheinlichkeit
Andererseits können Ereignisse und zufällige Prozesse nicht durch deterministische Prozesse in der Form „wenn A, dann B“ beschrieben werden. Statistiken werden verwendet, um die Häufigkeit der Assoziation zwischen A und B zu quantifizieren und die Beziehungen zwischen ihnen als Grad der Wahrscheinlichkeit darzustellen, der den Grad der objektiven Wahrscheinlichkeit einführt. Im Zuge der zunehmenden Probabilisierung von Ungewissheit und Zufälligkeit in der Medizin seit dem 18. Jahrhundert ist der Begriff „Wahrscheinlichkeit“ zu einem angesehenen Element der medizinischen Sprache, Methodik und Erkenntnistheorie geworden. Leider werden die beiden Arten von Wahrscheinlichkeiten, die subjektive Wahrscheinlichkeit und die objektive, in der Medizin nicht genau unterschieden, und das gleiche geschieht auch in anderen Disziplinen. Grundsätzlich bleibt, dass die wichtigste Bedeutung, die die Wahrscheinlichkeitstheorie in der Medizin, insbesondere in den Wahrscheinlichkeitskonzepten der Ätiologie, Epidemiologie, Diagnostik und Therapie, generiert hat, ihr Beitrag zum Verständnis und zur Darstellung biologischer Unfallfolgen ist.
Probabilistisch-kausale Analyse
Aus diesen Prämissen geht hervor, dass die klinische Diagnose nach der sogenannten hypothetisch-deduktiven Methode, DN genannt, gestellt wird[4] (deductive-nomological model[5]).Dies ist jedoch unrealistisch, da das in der klinischen Entscheidungsfindung verwendete medizinische Wissen kaum kausaldeterministische Gesetzmäßigkeiten enthält, um kausale Erklärungen zu ermöglichen und damit ua im Fachkontext klinische Diagnosen zu formulieren. Lassen Sie uns versuchen, den Fall unserer Mary Poppins erneut zu analysieren, diesmal versuchen wir es mit einem probabilistisch-kausalen Ansatz.
Betrachten wir eine Anzahl von Personen, einschließlich Personen, die über orofaziale Schmerzen berichten und im Allgemeinen eine Knochendegeneration des Kiefergelenks haben. Es kann jedoch auch andere scheinbar unabhängige Ursachen geben. Wir müssen die „Relevanz“, die diese kausalen Ungewissheiten für die Bestimmung einer Diagnose haben, mathematisch übersetzen.
Die beiläufige Relevanz
Dazu betrachten wir den Grad der kausalen Relevanz eines Ereignisses in Bezug auf ein Ereignis , wobei gilt:
- = Patienten mit Knochendegeneration des Kiefergelenks
- = Patienten, die über orofaziale Schmerzen berichten
- =Patienten ohne Knochendegeneration des Kiefergelenks.
Wir verwenden die bedingte Wahrscheinlichkeit , also die Wahrscheinlichkeit, dass das Ereignis erst eintritt, nachdem das Ereignis bereits eingetreten ist.
Mit diesen Prämissen ist die kausale Relevanz der Patientenstichprobe :
Wo
- gibt die Wahrscheinlichkeit an, dass einige Personen (von berücksichtigten Personen) an orofazialen Schmerzen leiden, die durch eine Knochendegeneration des Kiefergelenks verursacht werden,
während
- gibt die Wahrscheinlichkeit an, dass andere Personen (immer unter berücksichtigt) an orofazialen Schmerzen leiden, die durch etwas anderes als eine Knochendegeneration des Kiefergelenks bedingt sind.
Da aller Wahrscheinlichkeit nach ein Wert zwischen und ist, wird der Parameter eine Zahl zwischen und sein
Die Bedeutungen, die wir dieser Zahl geben können, sind wie folgt.
- wir haben die extremen Fälle (die in Wirklichkeit nie vorkommen), die sind:
- was darauf hinweist, dass die einzige Ursache für orofaziale Schmerzen die Knochendegeneration des Kiefergelenks ist,
- was darauf hindeutet, dass die Ursache für orofaziale Schmerzen niemals eine Knochendegeneration des Kiefergelenks ist, sondern etwas anderes,
- was darauf hinweist, dass die Wahrscheinlichkeit, dass orofaziale Schmerzen durch Knochendegeneration des Kiefergelenks oder auf andere Weise verursacht werden, genau gleich ist,
- und die Zwischenfälle (die die realistischen sind)
- was darauf hindeutet, dass die Ursache für orofaziale Schmerzen eher eine Knochendegeneration des Kiefergelenks ist,
- was darauf hindeutet, dass die Ursache für orofaziale Schmerzen eher nicht die Knochendegeneration des Kiefergelenks ist.
Zweiter klinischer Ansatz
(fahren Sie mit der Maus über die Bilder)
Also sei es dann die Wahrscheinlichkeit, in der Stichprobe unserer Personen Personen zu finden, die die Elemente aufweisen, die zu der oben genannten Menge gehören.
Um die Informationen aus diesem Datensatz zu nutzen, wird das Konzept der Aufteilung der kausalen Relevanz eingeführt:
Die Aufteilung der kausalen Relevanz
- Sei immer die Anzahl der Personen, für die wir die Analysen durchführen müssen, wenn wir (basierend auf bestimmten Bedingungen, wie unten erklärt) diese Gruppe in Teilmengen mit aufteilen, wird ein Cluster erstellt, der als "Partitionsmenge" bezeichnet wird:
wobei mit der Symbolik anzeigt, dass die Unterklasse in enthalten ist. Die Partition muss, um als Partition mit kausaler Relevanz definiert zu werden, diese Eigenschaften haben:
- Für jede Unterklasse muss die Bedingung gelten, dh die Wahrscheinlichkeit, in der Untergruppe eine Person zu finden, die die zur Menge gehörenden Symptome, Krankheitszeichen und Elemente aufweist. Eine solche kausal relevante Partition wird als homogen bezeichnet.
- Jede Teilmenge muss „elementar“ sein, d. h. sie darf nicht weiter in andere Teilmengen unterteilt werden, denn wenn diese existierten, hätten sie keine kausale Bedeutung.
Nehmen wir nun beispielsweise an, dass die Populationsstichprobe , zu der unsere gute Patientin Mary Poppins gehört, eine Kategorie von Probanden im Alter von 20 bis 70 Jahren ist. Wir nehmen auch an, dass wir in dieser Population diejenigen haben, die die Elemente präsentieren, die zu der gehören Datensatz die den oben genannten Labortests entsprechen und precisa in 'The logic of classical language'.
Nehmen wir an, dass wir in einer Stichprobe von 10.000 Probanden von 20 bis 70 eine Inzidenz von 30 Probanden haben, die klinische Anzeichen von und zeigen. Wir haben es vorgezogen, diese Berichte zur Demonstration des probabilistischen Prozesses zu verwenden, da in der Literatur die Daten bzgl Klinische Anzeichen und Symptome für Kiefergelenkserkrankungen weisen unserer Meinung nach eine zu große Variation sowie eine zu hohe Inzidenz auf.[6][7][8][9][10][11]
Ein Beispiel für eine Partition mit vermuteter Wahrscheinlichkeit, bei der eine Kiefergelenksdegeneration (Grad.TMJ) in Verbindung mit Kiefergelenkserkrankungen (TMDs) auftritt, wäre die folgende:
| Wo | |||
| Wo | |||
| Wo | |||
| Wo |
- «Eine homogene Partition stellt das bereit, was wir gewöhnlich Differentialdiagnose nennen.»
Klinische Situationen
Diese bedingten Wahrscheinlichkeiten demonstrieren, dass jede der vier Unterklassen der Partition kausal relevant für die Patientendaten in der Bevölkerungsstichprobe ist. Angesichts der oben erwähnten Partition der Referenzklasse haben wir die folgenden klinischen Situationen:
- Mary Poppins Degeneration des Kiefergelenks Kiefergelenkserkrankungen
- Mary Poppins Degeneration des Kiefergelenks keine Kiefergelenkserkrankungen
- Mary Poppins keine Degeneration des Kiefergelenks Kiefergelenkserkrankungen
- Mary Poppins keine Degeneration des Kiefergelenks keine Kiefergelenkserkrankungen
Um zu der obigen endgültigen Diagnose zu gelangen, führten wir eine probabilistisch-kausale Analyse des Gesundheitszustands von Mary Poppins durch, deren Ausgangsdaten waren.
Im Allgemeinen können wir von einem logischen Prozess sprechen, in dem wir die folgenden Elemente untersuchen:
- ein Individuum:
- seinen Anfangsdatensatz
- eine Populationsstichprobe , zu der es gehört,
- eine Basiswahrscheinlichkeit
An dieser Stelle sollten wir zu spezialisierte Argumente einführen, die den Leser vom Thema ablenken würden, die aber eine hohe epistemische Bedeutung haben, für die wir versuchen werden, den am besten beschriebenen logischen Faden des Analysandum/Analysans-Konzepts herauszuziehen. Die probabilistisch-kausale Analyse von ist dann ein Paar der folgenden logischen Formen (Analysandum / Analysans[12]):
- Analysand : ist eine logische Form, die zwei Parameter enthält: Wahrscheinlichkeit , eine Person auszuwählen, die die Symptome und Elemente hat, die zur Menge gehören, und die generische Person , die für diese Symptome anfällig ist.
- Analysator : ist eine logische Form, die drei Parameter enthält: die Partition , die generische Person , die zur Populationsstichprobe gehört, und (Wissensbasis), die einen Satz von Aussagen zur bedingten Wahrscheinlichkeit enthält.
Beispielsweise kann daraus geschlossen werden, dass die definitive Diagnose die folgende ist:
bedeutet das, dass unsere Mary Poppins zu 95% von CMDs betroffen ist, da sie zusätzlich zu den positiven Daten eine Degeneration des Kiefergelenks hat
Schlussbetrachtungen
Wir haben einen langen und gewundenen Weg zurückgelegt, um die Komplexität besser zu verstehen, auf die der Kollege trifft, der mit der sehr schweren ethischen Verantwortung zu kämpfen hat, eine Diagnose zu stellen. Diese Aufgabe wird jedoch noch komplexer, wenn wir bei der Erstellung einer Differenzialdiagnose detailliert und sorgfältig vorgehen müssen. Hier betreten wir ein heikles Thema, das mit den erkenntnistheoretischen Inhalten zusammenhängt und über das zunächst im berichtet wurde "Introduction". Es handelt sich dabei um:
- Interdisziplinarität:
In der Wissenschaftspolitik ist allgemein anerkannt, dass wissenschaftsbasierte Problemlösungen interdisziplinäre Forschung (IDR) erfordern, wie sie das EU-Projekt Horizon 2020 vorschlägt[13].In einer aktuellen Studie konzentrieren sich die Autoren auf die Frage, warum Forscher kognitive und epistemische Schwierigkeiten bei der Durchführung von IDR haben. Es wird angenommen, dass der Verlust des philosophischen Interesses an der Erkenntnistheorie interdisziplinärer Forschung durch ein philosophisches Wissenschaftsparadigma namens "Physics Paradigm of Science" verursacht wird, das die Anerkennung wichtiger IDR-Änderungen sowohl in der Wissenschaftsphilosophie als auch in der Forschung verhindert. Das vorgeschlagene alternative philosophische Paradigma, genannt „Engineering Paradigm of Science“, macht alternative philosophische Annahmen über Aspekte wie den Zweck der Wissenschaft, den Charakter des Wissens, die epistemischen und pragmatischen Kriterien für die Akzeptanz von Wissen und die Rolle technologischer Werkzeuge. Folglich benötigen wissenschaftliche Forscher sogenannte metakognitive Gerüste, die ihnen bei der Analyse und Rekonstruktion der Konstruktion von „Wissen“ in verschiedenen Disziplinen helfen. In der interdisziplinären Forschung helfen metakognitive Gerüste der interdisziplinären Kommunikation, zu analysieren und zu artikulieren, wie die Disziplin Wissen aufbaut.[14][15]
Dieses Konzept knüpft an das zuvor diskutierte Thema an, bei dem sich der Kollege seiner eigenen „subjektiven Unsicherheit“ (aufgrund einer klassischen Logiksprache „krank oder gesund“) und seiner „objektiven Unsicherheit“ (aufgrund einer probabilistischen Logiksprache „ wahrscheinlich krank oder wahrscheinlich gesund"). Es ist nicht kompliziert, diese Behauptung zu beweisen: Die Ungewissheit, von der wir sprechen, ergibt sich aus der Tatsache, dass die erwähnten Elemente, Behauptungen, Daten, Klassen und Unterklassen den Apparat der Logik der Sprache der Wahrscheinlichkeitstheorie bilden: Analysandum und Analysan sind Elemente, die in einer bestimmten Welt existieren, und in diesem Fall in einem zahnmedizinischen Kontext, in dem das Element des Prozesses weist unbestreitbar nur in einem spezifischen zahnmedizinischen Kontext auf ein "Basiswissen" hin.
Diese vom Zahnarzt bestätigte Schlussfolgerung lautete wie folgt:
oder besser: ich bin zu 95% der Überzeugung, dass Mary Poppins von TMDs betroffen ist, da sie zusätzlich zur Positivität der Daten eine Degeneration des Kiefergelenks hat Doch etwas Seltsames passiert, denn aus dem Nichts fordert ein Forscher, der „metakognitive Gerüste“[16] für eine Umsetzung in die Analyse und Rekonstruktion des Aufbaus von „Wissen“ in verschiedenen Disziplinen einsetzt, vom Zahnarzt eine Antwort auf folgende Frage:
«Gibt es eine andere Welt oder einen Kontext, parallel zu Ihrer, in der es neben den D-Daten weitere Ihnen unbekannte Daten gibt?»
|
und erhöhen Sie die Dosis: Unterziehen Sie Mary Poppins den folgenden trigeminalen elektrophysiologischen Tests, beschriften Sie sie wie zuvor für die Satzdaten Generieren eines weiteren Satzes, der eine Zahl enthält von unbekannten Daten (nicht zum reinen Dentalbereich gehörend) wodurch ein völlig neuer Satz entsteht, den wir nennen werden (genannt gerade aufgrund des Vorhandenseins von Daten, die dem zahnmedizinischen Kontext unbekannt sind).
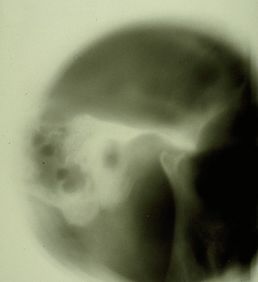
Positiver radiologischer Bericht des Kiefergelenks in Abbildung 2
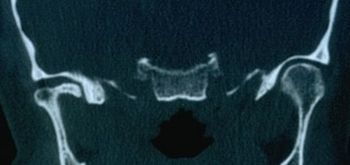
Positiver CT-Bericht des Kiefergelenks in Abbildung 3
Positiver axiographischer Bericht der Kondylenspuren in Abbildung 4
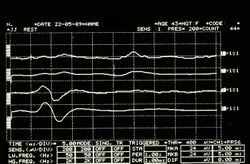
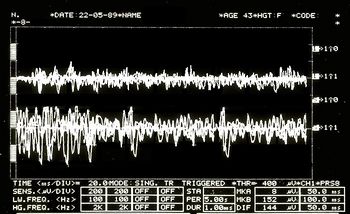
Asymmetrisches EMG-Interferenzmuster in Abbildung 5
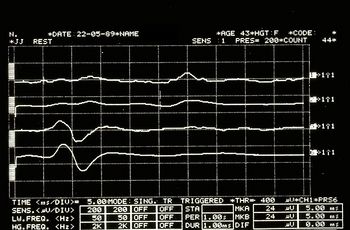
Kieferruck in Abbildung 6
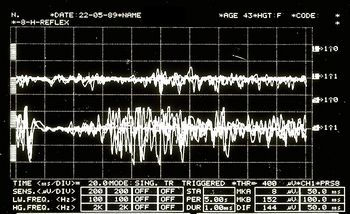
Mechanische Ruhezeit in Abbildung 7
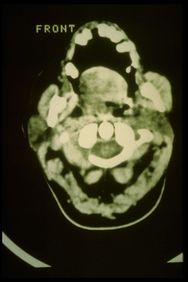
CT rechter Massetermuskel in Abbildung 8
Dritter klinischer Ansatz
(fahren Sie mit der Maus über die Bilder)
Auf diese Weise wurde gezeigt, dass zwangsläufig
Indem wir diese Begrenzungslinie des Fachkontextes untersuchen, werden wir einen Bereich in ihrer Nähe schaffen, den wir die „Fuzzy-Zone“ oder „Fuzzy-Logik“ nennen werden, die wir im nächsten Kapitel besprechen werden.
«... wie es scheint, werden wir nicht einmal mit einer probabilistischen Sprachlogik in der Lage sein, eine genaue Diagnose zu definieren.»
(in der Tat sollten wir aus diesem Grund auch darüber nachdenken Fuzzy Logic Language) |
- ↑ Vázquez-Delgado E, Cascos-Romero J, Gay-Escoda C, «Myofascial pain associated to trigger points: a literature review. Part 2: differential diagnosis and treatment», in Med Oral Patol Oral Cir Bucal, 2007».
PMID:20173729
DOI:10.4317/medoral.15.e639 - ↑ Thoppay J, Desai B, «Oral burning: local and systemic connection for a patient-centric approach», in EPMA J, 2019».
PMID:30984309 - PMCID:PMC6459460
DOI:10.1007/s13167-018-0157-3 - ↑ Sadegh-Zadeh Kazem, «Handbook of Analytic Philosophy of Medicine», Springer, 2012, Dordrecht».
ISBN: 978-94-007-2259-0
DOI:10.1007/978-94-007-2260-6 . - ↑ Sarkar S, «Nagel on Reduction», in Stud Hist Philos Sci, 2015».
PMID:26386529
DOI:10.1016/j.shpsa.2015.05.006 - ↑ DN model of scientific explanation, also known as Hempel's model, Hempel–Oppenheim model, Popper–Hempel model, or covering law model
- ↑ Pantoja LLQ, De Toledo IP, Pupo YM, Porporatti AL, De Luca Canto G, Zwir LF, Guerra ENS, «Prevalence of degenerative joint disease of the temporomandibular joint: a systematic review», in Clin Oral Investig, 2019».
PMID:30311063
DOI:10.1007/s00784-018-2664-y - ↑ De Toledo IP, Stefani FM, Porporatti AL, Mezzomo LA, Peres MA, Flores-Mir C, De Luca Canto G, «Prevalence of otologic signs and symptoms in adult patients with temporomandibular disorders: a systematic review and meta-analysis», in Clin Oral Investig, 2017».
PMID:27511214
DOI:10.1007/s00784-016-1926-9 - ↑ Bonotto D, Penteado CA, Namba EL, Cunali PA, Rached RN, Azevedo-Alanis LR, «Prevalence of temporomandibular disorders in rugby players», in Gen Dent».
PMID:31355769 - ↑ da Silva CG, Pachêco-Pereira C, Porporatti AL, Savi MG, Peres MA, Flores-Mir C, De Luca Canto G, «Prevalence of clinical signs of intra-articular temporomandibular disorders in children and adolescents: A systematic review and meta-analysis», in Am Dent Assoc, 2016». - PMCID:26552334
DOI:10.1016/j.adaj.2015.07.017 - ↑ Gauer RL, Semidey MJ, «Diagnosis and treatment of temporomandibular disorders», in Am Fam Physician, 2015».
PMID:25822556 - ↑ Kohlmann T, «Epidemiology of orofacial pain», in Schmerz, 2002».
PMID:12235497
DOI:10.1007/s004820200000 - ↑ Westmeyer H, «The diagnostic process as a statistical-causal analysis», in APA, 1975».
DOI:10.1007/BF00139821
This is an Open Access resource! - ↑ European Union, Horizon 2020
- ↑ Boon M, Van Baalen S, «Epistemology for interdisciplinary research - shifting philosophical paradigms of science», in Eur J Philos Sci, 2019».
DOI:10.1007/s13194-018-0242-4 9(1):16. - ↑ Boon M, «An engineering paradigm in the biomedical sciences: Knowledge as epistemic tool», in Prog Biophys Mol Biol, 2017».
DOI:10.1016/j.pbiomolbio.2017.04.001 - ↑ Boon M, Van Baalen S, «Epistemology for interdisciplinary research - shifting philosophical paradigms of science», in Eur J Philos Sci, 2019».
PMID:30873248 - PMCID:PMC6383598
DOI:10.1007/s13194-018-0242-4
This is an Open Access resource!
particularly focusing on the field of the neurophysiology of the masticatory system