Fuzzy-Sprachlogik

Home

Scientific project

Social project

Our story

Scientific community

Book index

Our network

Frisardi Masticationpedia Network

Fontana Masticationpedia Network

Ed. Lab

Donate

Contact

Change language

[[|German]]

[[|Spanish]]

[[|French]]

[[|Italian]]

Fuzzy-Sprachlogik

In diesem Kapitel werden wir uns mit der Fuzzy-Logik beschäftigen. Fuzzy heißt sie, weil sie sich durch Gradualität auszeichnet: Einem Objekt kann eine Eigenschaft zugeordnet werden, die unterschiedliche Wahrheitsgrade haben kann.

Im ersten Teil dieses Kapitels wird die Bedeutung der abgestuften Wahrheit begrifflich erörtert, während wir uns im zweiten Teil mit dem mathematischen Formalismus beschäftigen, indem wir die Zugehörigkeitsfunktion $\mu _{\displaystyle {\tilde {A}}}(x)$ ist das Element, das es uns ermöglicht, die Nuancen dieser Sprachlogik mathematisch zu synthetisieren. Es konnte gezeigt werden, dass mit Fuzzy Reasoning, im Gegensatz zu früheren Sprachlogiken, Diagnosen weniger Unsicherheit aufweisen. Trotzdem bleibt das Bedürfnis, die Sprachmethode weiter zu verfeinern und mit weiteren "Logiken" anzureichern.

 

 

Einführung

Wir sind so weit gekommen, weil wir als Kolleginnen und Kollegen sehr oft mit Verantwortungen und Entscheidungen konfrontiert sind, die sehr schwer zu treffen sind und Themen wie Gewissen, Intelligenz und Demut ins Spiel kommen. In einer solchen Situation sind wir jedoch mit zwei ebenso schwierigen Hindernissen konfrontiert, um die einer $KB$ (Wissensbasis) zu bewältigen, wie wir im Kapitel „Logik der probabilistischen Sprache“ besprochen haben, die in der Zeit begrenzt ist, die wir in $KB_{t}$ und eins kodifizieren $KB$ im konkreten Kontext eingeschränkt ($KB_{c}$). Diese beiden erkenntnistheoretischen Parameter charakterisieren das wissenschaftliche Zeitalter, in dem wir leben. Außerdem sind sowohl $KB_{t}$ als auch $KB_{c}$ abhängige Variablen unserer Phylogenie und insbesondere unserer konzeptionellen Plastizität und Einstellung zu Veränderungen.

«Ich folge dir nicht»
(Ich gebe Ihnen ein praktisches Beispiel)

• Wie viel Forschung gibt es zum Thema „Fuzzy-Logik“?

Pubmed antwortet mit 2862 Artikeln in den letzten 10 Jahren, sodass wir sagen können, dass unserer aktuell und ausreichend aktualisiert ist. Wenn wir jedoch die Aufmerksamkeit auf ein bestimmtes Thema wie „Temporandibuläre Störungen“ lenken möchten, antwortet die Datenbank mit bis zu 2.235 Artikeln. Wenn wir also ein anderes Thema wie „orofaziale Schmerzen“ überprüfen möchten, gibt uns Pubmed 1.986 Artikel. Das bedeutet, dass die $KB_{t}$ für diese drei Themen in den letzten 10 Jahren ausreichend aktualisiert wurde.

Wenn wir nun die Verbindung zwischen den Themen überprüfen wollten, werden wir feststellen, dass $KB_{c}$ in den Kontexten Folgendes sein wird:

1. $KB_{c}=$'Temporandibuläre Erkrankungen UND orofaziale Schmerzen'$\rightarrow$ 9 Artikel in den letzten 10 Jahren
2. $KB_{c}=$ 'Kiefermandibuläre Erkrankungen UND orofaziale Schmerzen UND Fuzzy-Logik' 0 Artikel in den letzten 10 Jahren

Das Beispiel bedeutet, dass die $KB_{t}$ einzeln für die drei Themen relativ aktuell ist, während sie dramatisch abnimmt, wenn die Themen zwischen Kontexten zusammengeführt werden, und zwar auf 9 Artikel für Punkt 1 und sogar auf 0 Artikel für Punkt 2. Also die $KB_{t}$ ist eine zeitabhängige Variable, während die $KB_{c}$ eine kognitive Variable ist, die von unserer Eignung für den Fortschritt der Wissenschaft abhängig ist, wie unter anderem bereits im Kapitel „Einführung“ erwähnt.

«du hast mich fast überzeugt»
(warten wir es ab)

Wir beendeten das vorige Kapitel mit der Feststellung, dass die Logik einer klassischen Sprache und anschließend die Wahrscheinlichkeitslogik uns beim Fortschritt der medizinischen Wissenschaft und Diagnostik sehr geholfen haben, aber implizit die Grenzen ihrer eigenen Sprachlogik in sich tragen, die die Vision einschränken das biologische Universum. Wir haben auch verifiziert, dass mit der Logik einer klassischen Sprache – sozusagen aristotelisch – die daraus abgeleitete logische Syntax in der Diagnostik unserer Mary Poppins der klinischen Schlussfolgerung in der Tat Grenzen setzt.

$\{a\in x\mid \forall {\text{x}}\;A({\text{x}})\rightarrow {B}({\text{x}})\vdash A(a)\rightarrow B(a)\}$ (siehe Kapitel Classical Language's Logic),

argumentiert, dass: „jeder normale Patient $\forall {\text{x}}$ , der bei der Röntgenuntersuchung des Kiefergelenks $\mathrm {\mathcal {A}} ({\text{x}})$ positiv ist, TMDs $\rightarrow \mathrm {\mathcal {B}} ({\text{x}})$ hat, als direkte Folge $\vdash$ Mary Poppins positiv ist (und auch eine „normale“ Patientin ist) auf der TMJ-Röntgenaufnahme $A(a)$ dann Mary Auch Poppins ist von TMDs $\rightarrow {\mathcal {B}}(a)$ betroffen

Die Einschränkung des eingeschlagenen logischen Pfades hat uns veranlasst, einen alternativen Pfad einzuschlagen, bei dem die Bivalenz oder Binärnatur der klassischen Sprachlogik vermieden und ein probabilistisches Modell verfolgt wird. Der Zahnarztkollege änderte tatsächlich das Vokabular und bevorzugte eine Schlussfolgerung wie:

$P(D|Deg.TMJ\cap TMDs)=0.95$

und das heißt, dass unsere Mary Poppins zu 95 % von TMDs betroffen ist, da sie eine Degeneration des Kiefergelenks hat, was durch die Positivität der Daten $D=\{\delta _{1},\dots \delta _{4}\}$ in einer Bevölkerungsstichprobe $n$ unterstützt wird. Wir haben dies jedoch auch im Prozess der Konstruktion der Wahrscheinlichkeitslogik festgestellt (Analysandum $=\{P(D),a\}$, der es uns ermöglichte, die oben genannten differenzialdiagnostischen Schlussfolgerungen zu formulieren und die plausibelste auszuwählen, gibt es ein entscheidendes Element für den gesamten Analysand $=\{\pi ,a,KB\}$, das durch den Begriff $KB$ repräsentiert wird, der insbesondere auf eine „Wissensbasis“ des Kontexts hinweist die Logik der probabilistischen Sprache wird aufgebaut.

Wir schlussfolgerten daher, dass der Zahnarztkollege sich vielleicht seiner eigenen „subjektiven Unsicherheit“ (betroffen von TMDs oder _nOP?) und „objektiver Unsicherheit“ (wahrscheinlich stärker betroffen von CMDs oder _nOP?) hätte bewusst werden sollen.

• Warum sind wir zu diesen kritischen Schlussfolgerungen gekommen?

Für eine weit verbreitete Form der Darstellung der Realität, gestützt durch die Aussage maßgeblicher Persönlichkeiten, die ihre Kritikalität bestätigen. Daraus ist eine Vision der Realität entstanden, die auf den ersten Blick für eine medizinische Sprache ungeeignet erscheint; tatsächlich können Ausdrücke wie „ungefähr 2“ oder „mäßig“ berechtigte Verwirrung hervorrufen und als anachronistische Rückkehr zu vorwissenschaftlichen Konzepten erscheinen. Im Gegenteil, die Verwendung von Fuzzy-Zahlen oder Behauptungen erlaubt es, wissenschaftliche Daten in Kontexten zu behandeln, in denen nicht von „Wahrscheinlichkeit“, sondern nur von „Möglichkeit“ gesprochen werden kann.

«Wahrscheinlichkeit oder Möglichkeit?»

Fuzzy Wahrheit

In dem ehrgeizigen Versuch, die menschliche Rationalität mathematisch zu übersetzen, dachte man Mitte des 20. Jahrhunderts daran, den Begriff der klassischen Logik durch die Formulierung der Fuzzy-Logik zu erweitern. Die Fuzzy-Logik betrifft die Eigenschaften, die wir als „Gradualität“ bezeichnen könnten, d. h. die einem Objekt mit unterschiedlichen Graden zugeschrieben werden können. Beispiele sind die Eigenschaften „krank sein“, „Schmerzen haben“, „groß sein“, „jung sein“ und so weiter.

Mathematisch erlaubt uns die Fuzzy-Logik, jeder Aussage einen Wahrheitsgrad zwischen $0$ und $1$ zuzuschreiben. Das klassischste Beispiel zur Erklärung dieses Konzepts ist das Alter: Wir können sagen, dass ein Neugeborenes einen „Jugendgrad“ von $1$ hat, ein Achtzehnjähriger von $0,8$, ein Sechzigjähriger von $0,4$ und so weiter

Im Kontext der klassischen Logik hingegen gelten die Aussagen:

• • ein Zehnjähriger ist jung
  • ein Dreißigjähriger ist jung

sind beide wahr. Im Fall der klassischen Logik (die nur die beiden wahren oder falschen Daten zulässt) würde dies jedoch bedeuten, dass der Säugling und der Dreißigjährige gleich jung sind. Was offensichtlich falsch ist.

Die Bedeutung und der Charme der Fuzzy-Logik ergeben sich aus der Tatsache, dass sie in der Lage ist, die Unsicherheit, die einigen Daten der menschlichen Sprache innewohnt, in mathematischen Formalismus zu übersetzen und „elastische“ Konzepte (wie fast hoch, ziemlich gut usw.) zu codieren um sie für Computer verständlich und handhabbar zu machen.

Mengenlehre

Wie im vorigen Kapitel erwähnt, ist der Grundbegriff der Fuzzy-Logik der der Multivalenz, d. h. im Sinne der Mengenlehre die Möglichkeit, dass ein Objekt auch nur teilweise zu einer Menge und damit auch zu mehreren Mengen mit unterschiedlichem Grad gehören kann . Erinnern wir uns von Anfang an an die Grundelemente der Theorie der gewöhnlichen Mengen. Wie man sehen wird, erscheinen in ihnen die formalen Ausdrücke der Prinzipien der aristotelischen Logik, an die im vorigen Kapitel erinnert wurde.

Quantifizierer

• Zugehörigkeit: dargestellt durch das Symbol $\in$ (gehört dazu), - zum Beispiel gehört die Zahl 13 zur Menge der ungeraden Zahlen $\in$, $13\in Odd$0
• Nichtmitgliedschaft: dargestellt durch das Symbol $\notin$ (Es gehört nicht dazu)
• Inklusion: Dargestellt durch das Symbol $\subset$ (ist Inhalt), - zum Beispiel ist die ganze $A$ in der größeren Menge $U$, $A\subset U$enthalten (in diesem Fall sagt man, dass $A$ eine Teilmenge von $U$ ist
• Universalquantor, der durch das Symbol $\forall$ (für jeden) gekennzeichnet ist
• Demonstration, die durch das Symbol $\mid$ (so dass) angezeigt wird

Operatoren festlegen

Angesichts des gesamten Universums $U$ geben wir mit $x$ sein generisches Element an$x\in U$, so dass; dann betrachten wir zwei Teilmengen $A$ und $B$ intern zu $U$, so dass $A\subset U$ und $B\subset U$

	Vereinigung: dargestellt durch das Symbol $\cup$, zeigt die Vereinigung der beiden Mengen $A$ und $B$ an $(A\cup B)$. Sie wird durch alle Elemente definiert, die zu $A$ und $B$ oder beiden gehören: $(A\cup B)=\{\forall x\in U\mid x\in A\land x\in B\}$
	Schnittpunkt: dargestellt durch das Symbol $\cap$, zeigt die Elemente an, die zu beiden Mengen gehören: $(A\cap B)=\{\forall x\in U\mid x\in A\lor x\in B\}$
	Unterschied: dargestellt durch das Symbol $-$, zum Beispiel zeigt $A-B$ alle Elemente von $A$ außer denen, die mit $B$ geteilt werden
	Komplementär: dargestellt durch einen Balken über dem Namen der Sammlung, zeigt es mit ${\bar {A}}$ das Komplement von $A$ an, d. h. die Menge der Elemente, die zum gesamten Universum gehören, außer denen von $A$, in Formeln: ${\bar {A}}=U-A$

Die Theorie der Fuzzy-Sprachlogik ist eine Erweiterung der klassischen Mengenlehre, in der jedoch die Prinzipien der Widerspruchsfreiheit und des ausgeschlossenen Dritten nicht gelten. Denken Sie daran, dass in der klassischen Logik angesichts der Menge $A$ und ihrer komplementären ${\bar {A}}$ das Prinzip der Widerspruchsfreiheit besagt, dass ein Element, das zur ganzen $A$ gehört, nicht gleichzeitig auch zu seiner komplementären ${\bar {A}}$ gehören kann; nach dem Prinzip des ausgeschlossenen Dritten jedoch bildet die Vereinigung einer ganzen $A$ und ihrer komplementären ${\bar {A}}$ das vollständige Universum $U$.

Mit anderen Worten, wenn irgendein Element nicht zum Ganzen gehört, muss es notwendigerweise zu seiner Ergänzung gehören.

Fuzzy-Set ${\tilde {A}}$ und Zugehörigkeitsfunktion $\mu _{\displaystyle {\tilde {A}}}(x)$

Wir wählen – als Formalismus – die Darstellung einer Fuzzy-Menge mit der „Tilde“: ${\tilde {A}}$. Eine Fuzzy-Menge ist eine Menge, bei der die Elemente einen „Grad“ der Zugehörigkeit haben (in Übereinstimmung mit der Fuzzy-Logik): einige können in die Menge aufgenommen werden bei 100 %, andere in niedrigeren Prozentsätzen.

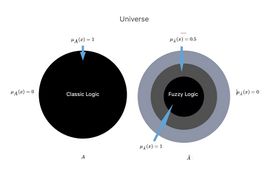
Um diesen Grad der Zugehörigkeit mathematisch darzustellen, gibt es die Funktion $\mu _{\displaystyle {\tilde {A}}}(x)$, die „Mitgliedschaftsfunktion“ genannt wird. Die Funktion $\mu _{\displaystyle {\tilde {A}}}(x)$ ist eine kontinuierliche Funktion, die im Intervall $[0;1]$ definiert ist, wo sie ist:

• $\mu _{\tilde {A}}(x)=1\rightarrow$ wenn $x$ vollständig in $A$ enthalten ist (diese Punkte werden "Kern" genannt, sie zeigen plausible Prädikatswerte an).
• $\mu _{\tilde {A}}(x)=0\rightarrow$wenn $x$ nicht enthalten ist $A$
• $0<\mu _{\tilde {A}}(x)<1\;\rightarrow$ wenn $x$ teilweise in $A$ enthalten ist (diese Punkte werden 'Unterstützung' genannt, sie geben die möglichen Prädikatswerte an).
• if $x$ is partially contained in $A$ (these points are called 'support', they indicate the possible predicate values).

Die grafische Darstellung der Funktion $\mu _{\displaystyle {\tilde {A}}}(x)$ kann variiert werden; von solchen mit linearen Linien (dreieckig, trapezförmig) bis hin zu solchen in Form von Glocken oder „S“ (sigmoidal), wie in Abbildung 1 dargestellt, die das gesamte grafische Konzept der Zugehörigkeitsfunktion enthält

Abbildung 1: Arten von Graphen für die Zugehörigkeitsfunktion.

Die Unterstützungsmenge einer Fuzzy-Menge ist definiert als die Zone, in der der Zugehörigkeitsgrad $0<\mu _{\tilde {A}}(x)<1$ ergibt; Andererseits wird der Kern als der Bereich definiert, in dem der Grad der Zugehörigkeit den Wert $\mu _{\tilde {A}}(x)=1$ annimmt.

Die „Unterstützungsmenge“ stellt die für möglich erachteten Werte des Prädikats dar, während der „Kern“ die für plausibler erachteten Werte darstellt.

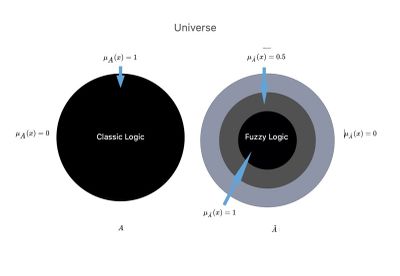
Wenn ${A}$ eine Menge im gewöhnlichen Sinne des oben beschriebenen Begriffs oder der klassischen Sprachlogik darstellen würde, könnte ihre Zugehörigkeitsfunktion nur die Werte $1$ oder $0$ annehmen, $\mu _{\displaystyle {A}}(x)=1\;\lor \;\mu _{\displaystyle {A}}(x)=0$ je nachdem, ob das Element $x$ zum betrachteten Ganzen gehört oder nicht. Abbildung 2 zeigt eine grafische Darstellung des klaren (starr definierten) oder unscharfen Konzepts der Mitgliedschaft, das deutlich an die Überlegungen von Smuts erinnert.

Gehen wir zurück zum konkreten Fall unserer Mary Poppins, in der wir eine Diskrepanz zwischen den Behauptungen des Zahnarztes und des Neurologen sehen und wir suchen einen Vergleich zwischen klassischer Logik und Fuzzy-Logik:

Abbildung 2: Darstellung des Vergleichs zwischen einem klassischen und einem Fuzzy-Ensemble.

Abbildung 2: Stellen wir uns das Wissenschaftsuniversum $U$ vor, in dem es zwei parallele Welten oder Kontexte gibt, ${A}$ und ${\tilde {A}}$

${A}=$ Im wissenschaftlichen Kontext das sogenannte „Crisp“, und wir haben in die Logik der klassischen Sprache überführt, in der der Arzt eine absolute wissenschaftliche Hintergrundinformation $KB$ mit einer klaren Trennlinie hat, die wir $KB_{c}$ genannt haben

${\tilde {A}}=$ In einem anderen wissenschaftlichen Kontext, der „Fuzzy-Logik“ genannt wird und in dem es eine Vereinigung zwischen der Teilmenge ${A}$ in ${\tilde {A}}$ gibt, die wir so weit gehen können zu sagen: Vereinigung zwischen $KB_{c}$.

Wir werden die folgenden Abzüge bemerkenswert bemerken:

• Klassische Logik im zahnmedizinischen Kontext ${A}$, in der nur ein logischer Prozess möglich ist, der als Ergebnis $\mu _{\displaystyle {A}}(x)=1$ liefert, oder $\mu _{\displaystyle {A}}(x)=0$ ist der Datenbereich $D=\{\delta _{1},\dots ,\delta _{4}\}$, reduziert auf Grundwissen $KB$ in der Menge ${A}$. Das bedeutet, dass es außerhalb der zahnmedizinischen Welt eine gibt void und dass der Begriff der Mengenlehre genau $\mu _{\displaystyle {A}}(x)=0$ geschrieben wird und was gleichbedeutend ist mit einem hohen Bereich von:

«Differentialdiagnosefehler»

• Fuzzy-Logik im zahnmedizinischen Kontext ${\tilde {A}}$, in der sie über das Grundwissen $KB$ hinaus repräsentiert werden des zahnmedizinischen Kontexts haben auch diejenigen, die teilweise aus der neurophysiologischen Welt $0<\mu _{\tilde {A}}(x)<1$ erworben wurden, das Vorrecht, ein Ergebnis $\mu _{\tilde {A}}(x)=1$ und ein Ergebnis $0<\mu _{\tilde {A}}(x)<1$ aufgrund von Grundwissen $KB$ zurückzugeben was an dieser Stelle durch die Vereinigung von $KB_{c}$ dentalen und neurologischen Kontexten repräsentiert wird. Das Ergebnis dieser wissenschaftlich-klinischen Umsetzung der Zahnheilkunde würde a
  «Reduzierung des differenzialdiagnostischen Fehlers»

Schlussbetrachtungen

Themen, die die Aufmerksamkeit des Lesers ablenken könnten, waren in der Tat wesentlich, um die Botschaft zu demonstrieren. Normalerweise, wenn sich irgendein mehr oder weniger brillanter Geist erlaubt, einen Stein in den Teich der Wissenschaft zu werfen, wird eine Schockwelle erzeugt, die typisch für die Periode von Kuhns außergewöhnlicher Wissenschaft ist, gegen die die meisten Mitglieder der internationalen wissenschaftlichen Gemeinschaft streiten. Mit gutem Glauben können wir sagen, dass dieses Phänomen – in Bezug auf die Themen, die wir hier ansprechen – in der Prämisse am Anfang des Kapitels gut dargestellt ist.

In diesen Kapiteln wurde eigentlich ein grundlegendes Thema für die Wissenschaft angesprochen: die Neubewertung, das spezifische Gewicht, das $P-value$ immer gegeben wurde, das Bewusstsein für wissenschaftliche / klinische Zusammenhänge, $KB_{c}$, einen elastischeren Weg der Fuzzy Logic eingeschlagen zu haben als die Klassischer, der die extreme Bedeutung von $KB$ und letztendlich die Vereinigung von Kontexten $KB_{c}$ erkennt, um seine diagnostische Kapazität zu erhöhen.

Im nächsten Kapitel werden wir bereit sein, einen ebenso faszinierenden Weg zu gehen: Er führt uns in den Kontext einer Systemsprachenlogik und erlaubt uns, unser Wissen nicht mehr nur in der klinischen Semiotik, sondern im Verständnis von System zu vertiefen Funktionen (vor kurzem wird es in neuromotorischen Disziplinen für die Parkinson-Krankheit evaluiert).In Masticationpedia werden wir natürlich über das Thema „Systeminferenz“ im Bereich des Kausystems berichten, wie wir im nächsten Kapitel mit dem Titel „Systemlogik“ nachlesen konnten.

Bibliography & references

Masticationpedia is a charity, a not-for-profit organization operating in dentistry medical research,
particularly focusing on the field of the neurophysiology of the masticatory system
 

Home

Introduction

Latest chapter

Ed. Lab

Donate

Contacts