Difference between revisions of "Siamo sicuri di sapere tutto?"
| (6 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{ | |||
{{main menu it | |||
|link to German= Hauptseite | |||
|link to Spanish= Pàgina Principal | |||
|link to French= Page d'accueil | |||
|link to English= Main Page | |||
}} | |||
==Riassunto== | |||
[[File:Question 2.jpg|left|150x150px]] | |||
Ci stiamo avvicinando alla conclusione della prima sezione di Masticationpedia che sostanzialmente ha avuto il compito di rappresentare lo status quo della diagnostica nel campo dei dolori Orofacciali e dei Disordini Temporomandibolari. Abbiamo anche presentato i primi ostacoli che si pongono di fronte ad una diagnosi corretta, dettagliate e rapita ma forse sfugge un pò al ricercatore e clinico che ci sono anche problemi e limitazioni fuori dal contesto clinico per esempio quando si pensa all'effetto dell'ordine dell'informazione presentata al medico per formulare la diagnosi. Conosciuto questo fenomeno cognitivo come possiamo rappresentarlo statisticamente? Purtroppo la statistica classica con il famoso ed inflazionato Teorema di Bayes non è adatto perchè le variabili non sono compatibili. Per questo motivo prima di passare alla presentazione degli ultimi due pazienti abbiamo evidenziato alcune anomalie di fondo. | Ci stiamo avvicinando alla conclusione della prima sezione di Masticationpedia che sostanzialmente ha avuto il compito di rappresentare lo status quo della diagnostica nel campo dei dolori Orofacciali e dei Disordini Temporomandibolari. Abbiamo anche presentato i primi ostacoli che si pongono di fronte ad una diagnosi corretta, dettagliate e rapita ma forse sfugge un pò al ricercatore e clinico che ci sono anche problemi e limitazioni fuori dal contesto clinico per esempio quando si pensa all'effetto dell'ordine dell'informazione presentata al medico per formulare la diagnosi. Conosciuto questo fenomeno cognitivo come possiamo rappresentarlo statisticamente? Purtroppo la statistica classica con il famoso ed inflazionato Teorema di Bayes non è adatto perchè le variabili non sono compatibili. Per questo motivo prima di passare alla presentazione degli ultimi due pazienti abbiamo evidenziato alcune anomalie di fondo. | ||
{{ArtBy| | |||
| autore = Gianni Frisardi | |||
| autore2 = Luca Fontana | |||
| autore3 = Flavio Frisardi | |||
| autore4 = | |||
| autore5 = | |||
| autore6 = | |||
| }} | |||
=== Introduzione === | === Introduzione === | ||
| Line 103: | Line 108: | ||
Il '''support set''' di un insieme fuzzy è definito come la zona in cui il grado di appartenenza risulta <math>0<\mu_ {\tilde {A}}(x) < 1</math>; il nucleo o core è invece definito come l'area in cui il grado di appartenenza assume valore <math>\mu_ {\tilde {A}}(x) = 1</math>. Il 'Support set' rappresenta i valori del predicato ritenuti '''possibili''', mentre il 'core' rappresenta quelli ritenuti più '''plausibili'''. | Il '''support set''' di un insieme fuzzy è definito come la zona in cui il grado di appartenenza risulta <math>0<\mu_ {\tilde {A}}(x) < 1</math>; il nucleo o core è invece definito come l'area in cui il grado di appartenenza assume valore <math>\mu_ {\tilde {A}}(x) = 1</math>. Il 'Support set' rappresenta i valori del predicato ritenuti '''possibili''', mentre il 'core' rappresenta quelli ritenuti più '''plausibili'''. | ||
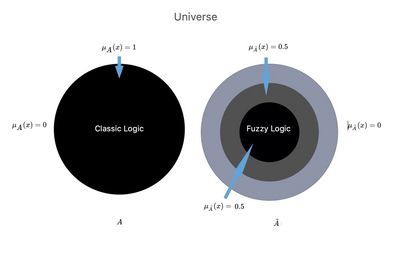
Se <math>{A}</math> rappresentasse un insieme nel senso ordinario del termine o nella logica del linguaggio classico precedentemente descritto, la sua funzione di appartenenza potrebbe assumere solo i valori <math>1</math> o <math>0</math> (Figura 1, <math>{A}</math>) <math>\mu_{\displaystyle {{A}}}(x)= 1 \; \lor \;\mu_{\displaystyle {{A}}}(x)= 0</math> a seconda che l'elemento 0 appartenga o meno al tutto, come considerato [[File: | Se <math>{A}</math> rappresentasse un insieme nel senso ordinario del termine o nella logica del linguaggio classico precedentemente descritto, la sua funzione di appartenenza potrebbe assumere solo i valori <math>1</math> o <math>0</math> (Figura 1, <math>{A}</math>) <math>\mu_{\displaystyle {{A}}}(x)= 1 \; \lor \;\mu_{\displaystyle {{A}}}(x)= 0</math> a seconda che l'elemento 0 appartenga o meno al tutto, come considerato | ||
[[File:Fuzzy2.jpg|alt=|thumb|400x400px|'''Figure 2:''' Representation of the comparison between a classical and fuzzy ensemble.]] | |||
Immaginiamo, adesso, che nell'Universo della Scienza <math>U</math> esistano due mondi o contesti paralleli <math>{A}</math> e <math>\tilde{A}</math> in cui per caso si trova la nostra paziente Mary Poppins ( vedi capitolo). | |||
<math>{A}=</math> Un mondo o contesto scientifico, il cosiddetto 'ben definito', della logica del linguaggio classico, in cui il medico ha un conoscenza scientifica di base assoluta '<math>KB</math>' con una chiara linea di demarcazione che raffigura l'area della proprio contesto che chiamiamo <math>KB_c</math> ( Knowledge Basic contest). In questo Universo siamo di fronte ad un unico mondo o contesto ( consideriamo quello odontoiatrico) e le risposte possono soltanto essere <math>\mu_{\displaystyle {{A}}}(x)= 1 \; \lor \;\mu_{\displaystyle {{A}}}(x)= 0</math> e dunque TMDs oppure noTMDs. | <math>{A}=</math> Un mondo o contesto scientifico, il cosiddetto 'ben definito', della logica del linguaggio classico, in cui il medico ha un conoscenza scientifica di base assoluta '<math>KB</math>' con una chiara linea di demarcazione che raffigura l'area della proprio contesto che chiamiamo <math>KB_c</math> ( Knowledge Basic contest). In questo Universo siamo di fronte ad un unico mondo o contesto ( consideriamo quello odontoiatrico) e le risposte possono soltanto essere <math>\mu_{\displaystyle {{A}}}(x)= 1 \; \lor \;\mu_{\displaystyle {{A}}}(x)= 0</math> e dunque TMDs oppure noTMDs. | ||
| Line 130: | Line 137: | ||
</ref> hanno rappresentato il fenomeno dell'effetto dell'ordine dell'informazione concludendo che I modelli cognitivi basati sui principi della probabilità quantistica hanno il potenziale per spiegare fenomeni paradossali che si verificano nelle scienze cognitive. In precedenza, i modelli quantistici sono stati utilizzati per tenere conto delle violazioni dei principi razionali del processo decisionale,<ref>Pothos, E. M., & Busemeyer, J. R. (2009). A quantum probability explanation for violations of “rational” decision theory. ''Proceedings of the Royal Society B'', 276(1165), 2171–2178.</ref> dei paradossi della combinazione concettuale,<ref>Aerts, D. (2009). Quantum structure in cognition. ''Journal of Mathematical Psychology'', 53, 314–348</ref> dei giudizi umani<ref>Khrennikov, A. Y. (2004). Information dynamics in cognitive, psychological, social and anomalous phenomena. Dordrecht, Netherlands: Kluwer Academic.</ref> e della percezione<ref>Atmanspacher, H., Filk, T., & Romer, H. (2004). Quantum zero features of bistable perception. ''Biological Cybernetics'', 90, 33–40.</ref> e che, comunque, il modello di inferenza quantistica può adattarsi perfettamente ai dati del compito decisionale medico di Bergus et al. (1998).<ref>Bergus, G. R., Chapman, G. B., Levy, B. T., Ely, J. W., & Oppliger, R. A. (1998). Clinical diagnosis and order of information. ''Medical Decision Making'', 18, 412–417.</ref>{{q2|Siamo ancora sicuri di sapere tutto?|}} | </ref> hanno rappresentato il fenomeno dell'effetto dell'ordine dell'informazione concludendo che I modelli cognitivi basati sui principi della probabilità quantistica hanno il potenziale per spiegare fenomeni paradossali che si verificano nelle scienze cognitive. In precedenza, i modelli quantistici sono stati utilizzati per tenere conto delle violazioni dei principi razionali del processo decisionale,<ref>Pothos, E. M., & Busemeyer, J. R. (2009). A quantum probability explanation for violations of “rational” decision theory. ''Proceedings of the Royal Society B'', 276(1165), 2171–2178.</ref> dei paradossi della combinazione concettuale,<ref>Aerts, D. (2009). Quantum structure in cognition. ''Journal of Mathematical Psychology'', 53, 314–348</ref> dei giudizi umani<ref>Khrennikov, A. Y. (2004). Information dynamics in cognitive, psychological, social and anomalous phenomena. Dordrecht, Netherlands: Kluwer Academic.</ref> e della percezione<ref>Atmanspacher, H., Filk, T., & Romer, H. (2004). Quantum zero features of bistable perception. ''Biological Cybernetics'', 90, 33–40.</ref> e che, comunque, il modello di inferenza quantistica può adattarsi perfettamente ai dati del compito decisionale medico di Bergus et al. (1998).<ref>Bergus, G. R., Chapman, G. B., Levy, B. T., Ely, J. W., & Oppliger, R. A. (1998). Clinical diagnosis and order of information. ''Medical Decision Making'', 18, 412–417.</ref>{{q2|Siamo ancora sicuri di sapere tutto?|}} | ||
{{bib}} | {{bib}} | ||
{{bib}} | {{bib}} | ||
Latest revision as of 18:20, 10 March 2024
Siamo sicuri di sapere tutto?
Riassunto
Ci stiamo avvicinando alla conclusione della prima sezione di Masticationpedia che sostanzialmente ha avuto il compito di rappresentare lo status quo della diagnostica nel campo dei dolori Orofacciali e dei Disordini Temporomandibolari. Abbiamo anche presentato i primi ostacoli che si pongono di fronte ad una diagnosi corretta, dettagliate e rapita ma forse sfugge un pò al ricercatore e clinico che ci sono anche problemi e limitazioni fuori dal contesto clinico per esempio quando si pensa all'effetto dell'ordine dell'informazione presentata al medico per formulare la diagnosi. Conosciuto questo fenomeno cognitivo come possiamo rappresentarlo statisticamente? Purtroppo la statistica classica con il famoso ed inflazionato Teorema di Bayes non è adatto perchè le variabili non sono compatibili. Per questo motivo prima di passare alla presentazione degli ultimi due pazienti abbiamo evidenziato alcune anomalie di fondo.
Introduzione
Nel corso dei precedenti capitoli di Masticationpedia abbiamo voluto rimarcare la complessità diagnostica nel campo dei Dolori Orofacciali e dei Disordini Temporomandibolari (TMDs) che a volte celano patologie neurologiche e/o sistemiche molto più gravi con un decorso diagnostico di decenni. Uno dei dati più eclatanti che vengo fuori dalle ricerche in letteratura è la la prevalenza della TMD elevata (30%-50%) in tutto il mondo[1] contestuale alla loro variabilità tra studi clinici ( 3-20%).[2][3][4][5] Ci si domanda, in primis: come mai così tanta variazione di prevalenza di TMDs nell popolazione tra i vari studi eseguiti in varie parti del mondo? E' forse un errore nella progettazione degli studi, di processi statistici oppure di conoscenza? Comunque sia, tutto ciò ha indotto la Comunità Scientifica Internazionale alla ricerca di nuovi paradigmi per arginare il danno diagnostico e terapeutico attraverso un modello chiamato 'Research Diagnostic Criteria' e siglato come 'RDC'. Al di là dell'esattezza concettuale del RDC nato esclusivamente per distingue il sano dal malato di TMDs, argomento che verrà trattato dettagliatamente nella successiva sezione di Masticationpedia, ci siamo trovati nella condizione di fare diagnosi di patologie gravi in pazienti precedentemente diagnosticati come DTMs.
Ciò significa che al di là dello RDC la complessità diagnostica nei casi in cui sussiste un disturbo dei sistema masticatorio ( click e scrosci della ATM, bruxismo, serramento, crossbite dentali ecc.) contestualmente alla sintomatologia dolorosa Orofacciale, la questione non è più rappresentabile con una statistica classica come quella di Bayes che sostanzialmente ha generato i valori predittivi positivi dello RDC.
Tanto è vero che si è dovuto organizzare un 'Consortium Network' replicati in vari meeting di studio [6][7][8][9][10][11] che sostanzialmente giungono alla seguente conclusione di R. Ohrbach and S.F. Dworkin[12]
Un ultimo tema è che la nostra comprensione dei disturbi specifici dell’ATM è in ritardo rispetto a quella dei disturbi del dolore. L’implicazione collettiva di questi temi è che ulteriore ricerca e sviluppo trarranno beneficio da un approccio programmatico comprensivo delle molteplici direzioni qui descritte così come di innumerevoli altre esistenti al di fuori dell’attuale quadro del consorzio.
Il fine di Masticationpedia è e sarà nel tempo, appunto, la richiesta espressa da Ohrbach and S.F. Dworkin[12] e cioè:
(vediamo qualche passaggio rilevante)
Prevalenza di TMDs
La prevalenza dei sintomi del disturbo temporomandibolare (TMDs) varia in modo significativo tra le popolazioni. Una recente revisione sistematica ha indicato che nella popolazione generale la prevalenza di avere almeno un segno clinico di TMD varia tra il 5 e il 60%.[13] Tuttavia, il dolore nella regione temporo-mandibolare è un segno clinico comune, che si verifica in circa il 10% della popolazione adulta.[14] Le cefalee primarie (emicrania e cefalea di tipo tensivo [TTH]), invece, colpiscono più di 2,5 miliardi di individui in tutto il mondo. Un recente studio globale ha classificato il mal di testa come la seconda causa principale di anni persi a causa della disabilità, dopo la lombalgia.[15] A livello globale, il numero di individui che soffrono di emicrania e TTH nel 2017 è stato stimato in 1,3 e 2,3 miliardi con una prevalenza rispettivamente del 15% e del 16%.[16]
Questi dati già indicano una certa incertezza dei numeri, incertezza che, come vedremo in seguito, diviene drammaticamente condizionante nel modelli di predicibilità Bayesani.
Inoltre gran parte degli studi precedenti sull’associazione del dolore correlato ai TMD e del mal di testa si sono basati sulle statistiche 'Frequentiste', modelli che rispetto all’approccio bayesiano, soffrono di alcune limitazioni, soprattutto la dipendenza da campioni di grandi dimensioni affinché le dimensioni degli effetti siano determinate con precisione.[17]
A quanto dice Javed Ashraf et al.[18] contrariamente alla metodologia 'Frequentista', la statistica bayesiana non fornisce un valore di risultato (fisso) ma piuttosto un intervallo contenente il coefficiente di regressione.[19] Questi intervalli, detti intervalli confidenza (CI), attribuiscono una probabilità alla migliore stima e a tutti i possibili valori delle stime dei parametri.[17]
Nello studio di Javed Ashraf et al.[18] gli autori utilizzando la metodologia bayesiana, hanno tentato di verificare l'esistenza della correlazione tra dolore correlato alla TMD con forti mal di testa (emicrania e TTH) in un periodo di follow-up di 11 anni. L'indagine Health 2000, condotta negli anni 2000 e 2001, ha incluso 9922 partecipanti invitati di età pari o superiore a 18 anni che vivevano nella Finlandia continentale.[20] L'associazione prospettica di mTMD al basale con la presenza di TTH al follow-up riscontrata nel presente studio è in linea con precedenti evidenze epidemiologiche, cliniche e fisiologiche. Precedenti studi epidemiologici hanno mostrato un’associazione tra dolore correlato alla TMD e TTH.[21] Clinicamente, il dolore correlato al TMD e il TTH condividono una combinazione di segni e sintomi distinti nella regione della testa e del viso, particolarmente evidenti per quanto riguarda mTMD e TTH. Queste caratteristiche cliniche comuni includono la dolorabilità alla palpazione dei muscoli masticatori nel caso della mTMD e dei muscoli pericranici nel caso della TTH durante le fasi attive di entrambe le condizioni.[22] Altre intersezioni cliniche tra mTMD e TTH includono l’età dei soggetti per quanto riguarda il picco di prevalenza,[23] l’intensità del dolore, la farmacoterapia[24] e persino il trattamento non farmacologico.[25] Nonostante alcune somiglianze cliniche e sovrapposizioni, sia la mTMD che la TTH sono entità patologiche distinte e Javed Ashraf[18] elegantemente conclude:
(la 'Interdisciplinarità' significa 'Contesto')
Contesti
Nei capitoli precedenti di Masticationpedia nel descrivere la complessità diagnostica abbiamo preso in considerazione un dato che risulterà essenziale quello dei contesti. Abbiamo visto come un soggetto malato sintomatico oppure asintomatico si pone davanti al medico che ascoltando il proprio racconto cerca di ricostruire l'andamento del 'Stato' del sistema organico per giungere ad una diagnosi certa. Contestualmente, però, abbiamo anche considerato l'enorme distanza di conoscenza scientifico clinica tra un contesto, quello odontoiatrico, e quello neurologico. Questi contesti impiegando una logica formale giungono alla convinzione della propria ragione diagnostica. L'assunto è che le asserzione che contribuisco ad edificare tale certezza sono ben diverse tra contesti. Per questo motivo nel capitolo 'Fuzzy language logic' abbiamo considerato un insieme ed una funzione di appartenenza .
Scegliamo - come formalismo - di rappresentare un insieme fuzzy con la 'tilde': . Un insieme fuzzy è un insieme in cui gli elementi hanno un 'grado' di appartenenza (coerente con la logica fuzzy), alcuni possono essere inclusi nell'insieme al 100%, altri in percentuali inferiori. A rappresentare matematicamente questo grado di appartenenza è la funzione chiamata 'Funzione di appartenenza'.
Immaginiamo che rappresenti un contesto e che è una funzione continua definita nell'intervallo dove:
- se è totalmente contenuta in (questi punti sono chiamati 'nucleus', essi indicano i valori plausibili del predicato ).
- se non è contenuto in
- se è parzialmente contenuto in (questi punti sono chiamati 'Support set' ed indicano i valori possibili del predicato possible predicate values).
Il support set di un insieme fuzzy è definito come la zona in cui il grado di appartenenza risulta ; il nucleo o core è invece definito come l'area in cui il grado di appartenenza assume valore . Il 'Support set' rappresenta i valori del predicato ritenuti possibili, mentre il 'core' rappresenta quelli ritenuti più plausibili.
Se rappresentasse un insieme nel senso ordinario del termine o nella logica del linguaggio classico precedentemente descritto, la sua funzione di appartenenza potrebbe assumere solo i valori o (Figura 1, ) a seconda che l'elemento 0 appartenga o meno al tutto, come considerato
Immaginiamo, adesso, che nell'Universo della Scienza esistano due mondi o contesti paralleli e in cui per caso si trova la nostra paziente Mary Poppins ( vedi capitolo).
Un mondo o contesto scientifico, il cosiddetto 'ben definito', della logica del linguaggio classico, in cui il medico ha un conoscenza scientifica di base assoluta '' con una chiara linea di demarcazione che raffigura l'area della proprio contesto che chiamiamo ( Knowledge Basic contest). In questo Universo siamo di fronte ad un unico mondo o contesto ( consideriamo quello odontoiatrico) e le risposte possono soltanto essere e dunque TMDs oppure noTMDs.
Nell'altro mondo o contesto scientifico chiamato 'Logica fuzzy', ci vine rappresentato un mondo o contesto di unione tra il sottoinsieme in tanto da poter affermare che i mondi si fondono parzialmente e di conseguenza anche i contesti si legano per dare vita ad una dei contesti unificati.
Noteremo le seguenti deduzionii:
- Logica classica nel contesto odontoiatrico in cui sarà possibile solo un processo logico che dia come risultato , ovvero essendo l'intervallo di dati ridotto alle conoscenze di base ( contesto scientifico/clinico odontoiatrico ) nell'insieme . Ciò significa che al di fuori del mondo o contesto odontoiatrico c'è un vuoto e che il termine di teoria degli insiemi è scritto esattamente e che è, sinonimo di rischio diagnostico.
- ''Logica fuzzy'' nel mondo in cui sono rappresentati oltre le conoscenze di base del contesto odontoiatrico anche quelli parzialmente acquisiti dal mondo neurofisiologico abbiamo che la funzione di appartenenza sarà determinata dalla sommatoria dei due contesti ed . In questo scenario la funzione di appartenenza sarà sempre nel range ma il dato uscente corrisponderà alla somma dei due contesti diminuendo, ovviamente, il rischio diagnostico.
(.....si certo un piccolo passo avanti se non ci fosse un altro ostacolo poco considerato quello dello 'Ordine dell'informazione' dei contesti)
Ordine dell'informazione
L’ordine delle informazioni gioca un ruolo cruciale nel processo di aggiornamento delle credenze nel tempo. Infatti, la presenza di effetti di ordine rende difficile un approccio classico o bayesiano all’inferenza.
Supponiamo di essere interessati a valutare la probabilità di un'ipotesi, , date due informazioni, e . Poiché la probabilità classica obbedisce alla proprietà commutativa, abbiamo il seguente modello:
Immaginiamo una decisione cognitiva diagnostica che prende un medico visitando un paziente con Dolore Orofacciale, a cui, solo dopo una anamnesi ed una dettagliata analisi clinico funzionale del sistema masticatorio in cui emergono discrepanze occlusali , vengono presentati i dati elettrofisiologici di laboratorio che mostrano una asimmetria delle risposte trigeminali da cui formulare una prima ipotesi di DTMs. la predicibilità che questa ipotesi sia vera ha una probabilità che deriva dal Terema di Bayes letto nel seguente modo:
La probabilità dell'ipotesi che un paziente sia affetto da DTMs se coesiste un primo evento (discrepanze occlusali) ed un secondo evento (asimmetria risposte trigeminali) è data da:
Ciò significa che per il Bayes la probabilità di essere malato di una certa malattia ( Valore Predittivo Positivo) non cambia se si inverte l'ordine di presentazione delle informazioni in quanto nel Bayes le variabili e commutano perché compatibili. Come detto, se cambiamo l'ordine di presentazione dell'informazione il risultato non cambia mentre a livello cognitivo decisionale le cose non stanno proprio così. Il cambiare l'ordine di presentazione delle informazioni può cambiare totalmente l'ipotesi virando verso una diagnosi di neuropatia anziché di DTMs.
(......con il solito dubbio Amletico: chi dice che le asimmetria delle risposte trigeminali siano compatibili con una DTMs?)
Nella teoria quantistica, gli eventi possono essere definiti come compatibili o incompatibili. Nel caso in cui tutti gli eventi siano compatibili, la probabilità quantistica è identica alla probabilità classica. Decidere quando due eventi debbano essere trattati come compatibili o incompatibili è un’importante questione di ricerca. In un articolo molto interessante Jennifer S. Trueblood e Jerome R. Busemeyer[26] hanno rappresentato il fenomeno dell'effetto dell'ordine dell'informazione concludendo che I modelli cognitivi basati sui principi della probabilità quantistica hanno il potenziale per spiegare fenomeni paradossali che si verificano nelle scienze cognitive. In precedenza, i modelli quantistici sono stati utilizzati per tenere conto delle violazioni dei principi razionali del processo decisionale,[27] dei paradossi della combinazione concettuale,[28] dei giudizi umani[29] e della percezione[30] e che, comunque, il modello di inferenza quantistica può adattarsi perfettamente ai dati del compito decisionale medico di Bergus et al. (1998).[31]
- ↑ Ouanounou A, Goldberg M, Haas DA. Pharmacotherapy in Temporomandibular Disorders: A Review. J Can Dent Assoc. 2017 Jul;83:h7.
- ↑ Poveda Roda R, Bagan JV, Díaz Fernández JM, Hernández Bazán S, Jiménez Soriano Y. Review of temporomandibular joint pathology. Part I: classification, epidemiology and risk factors. Med Oral Patol Oral Cir Bucal. 2007 Aug 1;12(4):E292-8.
- ↑ Türp JC, Schindler HJ.Schmerz. Chronic temporomandibular disorders]. 2004 Apr;18(2):109-17. doi: 10.1007/s00482-003-0279-x.PMID: 15067530
- ↑ Fricton JR. The relationship of temporomandibular disorders and fibromyalgia: implications for diagnosis and treatment. Curr Pain Headache Rep. 2004 Oct;8(5):355-63. doi: 10.1007/s11916-996-0008-0.PMID: 15361319
- ↑ De Meyer MD, De Boever JA.The role of bruxism in the appearance of temporomandibular joint disorders].Rev Belge Med Dent (1984). 1997;52(4):124-38. PMID: 9709800
- ↑ International RDC/TMD Consortium (2000–2002) Mark Drangsholt, Samuel Dworkin, James Fricton, Jean-Paul Goulet, Kimberly Huggins, Mike John, Iven Klineberg, Linda LeResche, Thomas List, Richard Ohrbach, Octavia Plesh, Eric Schiffman, Christian Stohler, Keson Beng-Choon Tan, Edmond Truelove, Adrian Yap, Efraim Winocur NIDCR
- ↑ Miami Consensus Workshop (2009) Workgroup 1: Gary Anderson, Yoly Gonzalez, Jean-Paul Goulet, Rigmor Jensen, Bill Maixner, Ambra Michelotti, Greg Murray, Corine Visscher Workgroup 2: Sharon Brooks, Lars Hollender, Frank Lobbezoo, John Look, Sandro Palla, Arne Petersson, Eric Schiffman Workgroup 3: Werner Ceusters, Antoon deLaat, Reny deLeeuw, Mark Drangsholt, Dominic Ettlin, Charly Gaul, Thomas List, Don Nixdorf, Joanna Zakrzewska Workgroup 4: Sam Dworkin, Louis Goldberg, Jennifer Haythornthwaite, Mike John, Richard Ohrbach, Paul Pionchon, Marylee van der Meulen At large: Terri Cowley, Don Denucci, John Kusiak, Barry Smith, Peter Svensson International RDC/TMD Consortium Network and IADR Orofacial Pain Special Interest Group of the International Association for the Study of Pain Canadian Institute for Health Research National Center for Biomedical Ontology Medtech
- ↑ San Diego Consensus Workshop (2011) Workgroup 1: Gary Anderson, Reny deLeeuw, Jean-Paul Goulet, Rigmor Jensen, Frank Lobbezoo, Chris Peck, Arne Petersson, Eric Schiffman Workgroup 2: Justin Durham, Dominic Ettlin, Ambra Michelotti, Richard Ohrbach, Sandro Palla, Karen Raphael, Yoshihiro Tsukiyama, Corine Visscher Workgroup 3: Raphael Benoliel, Brian Cairns, Mark Drangsholt, Malin Ernberg, Lou Goldberg, Bill Maixner, Don Nixdorf, Doreen Pfau, Peter Svensson International RDC/TMD Consortium Network and IADR International Association for the Study of Pain Orofacial Pain Special Interest Group Canadian Institute for Health Research
- ↑ Iguacu Falls (Brazil) Workshop (2012) Workgroup 1: Reny deLeeuw, Jean-Paul Goulet, Frank Lobbezoo, Chris Peck, Eric Schiffman, Thomas List Workgroup 2: Justin Durham, Dominik Ettlin, Richard Ohrbach International RDC/TMD Consortium Network and IADR
- ↑ Seattle Symposium (2013) Raphael Benoliel, Brian Cairns, Werner Ceusters, Justin Durham, Eli Eliav, Ambra Michelotti, Richard Ohrbach, Karen Raphael International RDC/TMD Consortium Network and IADR
- ↑ Cape Town Symposium (2014) Per Alstergren, Jean-Paul Goulet, Frank Lobbezoo, Ambra Michelotti, Richard Ohrbach, Chris Peck, Eric Schiffman International RDC/TMD Consortium Network and IADR
- ↑ 12.0 12.1 R. Ohrbach and S.F. Dworkin. The Evolution of TMD Diagnosis. Past, Present, Future Monitoring Editor: Ronald Dubner. J Dent Res. 2016 Sep; 95(10): 1093–1101. Published online 2016 Jun 16. doi: 10.1177/0022034516653922 PMCID: PMC5004241, PMID: 27313164
- ↑ Ryan J, Akhter R, Hassan N, Hilton G, Wickham J, Ibaragi S. Epidemiology of temporomandibular disorder in the general population : a systematic review. Adv Dent Oral Health. 2019;10:1–13. doi: 10.19080/ADOH.2019.10.555787.
- ↑ Al-Jundi MA, John MT, Setz JM, Szentpétery A, Kuss O. Meta-analysis of treatment need for temporomandibular disorders in adult nonpatients. J Orofac Pain. 2008;22:97–107.
- ↑ GBD Diseases and injuries collaborators (2020) global burden of 369 diseases and injuries in 204 countries and territories, 1990–2019: a systematic analysis for the global burden of disease study 2019. Lancet. 2019;396:1204–1222
- ↑ James SL, Abate D, Abate KH, Abay SM, Abbafati C, et al. Global, regional, and national incidence, prevalence, and years lived with disability for 354 diseases and injuries for 195 countries and territories, 1990–2017: a systematic analysis for the Global Burden of Disease Study 2017. Lancet. 2018;392(10159):1789–1858. doi: 10.1016/S0140-6736(18)32279-7.
- ↑ 17.0 17.1 Buchinsky FJ, Chadha NK. To P or not to P: backing Bayesian statistics. Otolaryngol Head Neck Surg. 2017;157(6):915–918. doi: 10.1177/0194599817739260.
- ↑ 18.0 18.1 18.2 Javed Ashraf, Matti Närhi, Anna Liisa Suominen, Tuomas Saxlin. Association of temporomandibular disorder-related pain with severe headaches-a Bayesian view. Clin Oral Investing. 2022 Jan;26(1):729-738. doi: 10.1007/s00784-021-04051-y. Epub 2021 Jul 5.
- ↑ Depaoli S, van de Schoot R. Bayesian analyses: where to start and what to report. Eur Heal Psychol. 2014;16:75–84.
- ↑ Aromaa A, Koskinen S (2004) Health and functional capacity in Finland. Baseline results of the Health 2000 Health Examination Survey. Publications of the National Public Health Institute B12/2004. Helsinki
- ↑ Ciancaglini R, Radaelli G. The relationship between headache and symptoms of temporomandibular disorder in the general population. J Dent. 2001;29:93–98. doi: 10.1016/S0300-5712(00)00042-7
- ↑ Bendtsen L, Ashina S, Moore A, Steiner TJ. Muscles and their role in episodic tension-type headache: implications for treatment. Eur J Pain. 2016;20:166–175. doi: 10.1002/ejp.748.
- ↑ Costa Y-M, Porporatti A-L, Calderon P-S, Conti P-C-R, Bonjardim L-R. Can palpation-induced muscle pain pattern contribute to the differential diagnosis among temporomandibular disorders, primary headaches phenotypes and possible bruxism? Med oral, Patol oral y cirugía bucal. 2016;21:e59–65. doi: 10.4317/medoral.20826.
- ↑ Neblett R, Cohen H, Choi Y, Hartzell MM, Williams M, Mayer TG, Gatchel RJ. The central sensitization inventory (CSI): establishing clinically significant values for identifying central sensitivity syndromes in an outpatient chronic pain sample. J Pain. 2013;14:438–445. doi: 10.1016/j.jpain.2012.11.012.
- ↑ Fernández-De-Las-Peñas C, Cuadrado ML. Physical therapy for headaches. Cephalalgia. 2016;36:1134–1142. doi: 10.1177/0333102415596445.
- ↑ Jennifer S. Trueblood, Jerome R. Busemeyer. A Quantum Probability Account of Order Effects in Inference. Cognitive Science Volume 35, Issue 8 p. 1518-1552. https://doi.org/10.1111/j.1551-6709.2011.01197.x
- ↑ Pothos, E. M., & Busemeyer, J. R. (2009). A quantum probability explanation for violations of “rational” decision theory. Proceedings of the Royal Society B, 276(1165), 2171–2178.
- ↑ Aerts, D. (2009). Quantum structure in cognition. Journal of Mathematical Psychology, 53, 314–348
- ↑ Khrennikov, A. Y. (2004). Information dynamics in cognitive, psychological, social and anomalous phenomena. Dordrecht, Netherlands: Kluwer Academic.
- ↑ Atmanspacher, H., Filk, T., & Romer, H. (2004). Quantum zero features of bistable perception. Biological Cybernetics, 90, 33–40.
- ↑ Bergus, G. R., Chapman, G. B., Levy, B. T., Ely, J. W., & Oppliger, R. A. (1998). Clinical diagnosis and order of information. Medical Decision Making, 18, 412–417.



![{\displaystyle [0;1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc3bf59a5da5d8181083b228c8933efbda133483)