La logica del linguaggio probabilistico

Go to top

Riassunto

Il capitolo esplora la complessa relazione tra incertezza, probabilità e pratica medica. Il focus principale è su come il linguaggio e la logica probabilistici vengono applicati in medicina per affrontare e gestire l'inevitabile incertezza che caratterizza la diagnosi e il trattamento delle malattie.

L'incertezza in medicina è categorizzata in due tipi principali: soggettiva e casuale. L'incertezza soggettiva si riferisce allo stato di conoscenza e convinzione degli individui, che varia da persona a persona. La casualità, invece, riguarda eventi imprevedibili e la mancanza di una connessione certa tra causa ed effetto, fondamentale per la formulazione di diagnosi affidabili.

L'articolo sottolinea l'importanza di distinguere tra probabilità soggettiva, che si basa sulla percezione individuale, e probabilità oggettiva, che si appoggia su dati e prove empiriche. Questa distinzione è cruciale per interpretare correttamente i dati medici e per la formulazione di diagnosi e trattamenti basati su prove concrete piuttosto che su intuizioni o esperienze personali.

Un concetto chiave discusso è l'analisi probabilistico-causale, che tenta di quantificare la relazione tra eventi e processi casuali in ambito clinico. Questo approccio si basa sull'uso di probabilità condizionali e sulla partizione della rilevanza causale per affrontare le sfide diagnostiche, come distinguere tra diverse cause possibili di un sintomo o una condizione.

L'articolo tocca anche il tema dell'interdisciplinarietà nella ricerca scientifica, sottolineando come un approccio collaborativo e multidisciplinare sia fondamentale per risolvere problemi complessi e per una comprensione più profonda delle malattie. Inoltre, introduce la logica fuzzy come un potenziale strumento per gestire l'incertezza in situazioni dove le informazioni sono imprecise o incomplete, proponendola come un complemento alla logica probabilistica tradizionale nella pratica medica.

In conclusione, l'articolo riflette sulla necessità di un equilibrio tra oggettività e soggettività nella medicina, riconoscendo che entrambe giocano un ruolo cruciale nella gestione dell'incertezza. Attraverso l'analisi e l'applicazione dei concetti di probabilità soggettiva e oggettiva, insieme a metodologie come l'analisi probabilistico-causale e la logica fuzzy, i professionisti del settore medico possono aspirare a diagnosi più accurate e a trattamenti più efficaci, migliorando così la qualità dell'assistenza sanitaria.

Article by Gianni Frisardi · Riccardo Azzali · Flavio Frisardi

Logica del linguaggio probabilistico in medicina

Ogni idea scientifica, sia essa in medicina, architettura, ingegneria, chimica o qualsiasi altro campo, una volta applicata, è suscettibile a piccoli errori e incertezze. La matematica, attraverso la teoria della probabilità e l'inferenza statistica, contribuisce a gestire con precisione e a limitare queste incertezze. È importante tenere sempre presente che nei casi pratici "i risultati sono influenzati anche da molti altri fattori esterni alla teoria", come le condizioni iniziali e ambientali, gli errori sperimentali e altro ancora.

Le incertezze legate a questi fattori conferiscono un carattere probabilistico alla relazione tra teoria e osservazione. In ambito medico, esistono due tipi principali di incertezza che influenzano maggiormente le diagnosi: l'incertezza soggettiva e la casualità.^[1]^[2] Diventa quindi fondamentale, in questo contesto, distinguere tra queste due forme di incertezza e dimostrare come il concetto di probabilità assuma significati differenti in ciascuno di questi contesti. Cercheremo di illustrare questi concetti collegando ogni fase chiave all'approccio clinico discusso nei capitoli precedenti, con particolare riferimento agli ambiti odontoiatrico e neurologico, nel contestare il primato della diagnosi alla nostra amata Mary Poppins.

Incertezza soggettiva e casualità

Supponiamo di chiedere a Mary Poppins quale tra i due colleghi medici – il dentista e il neurologo – sia nel giusto.

Tale domanda genererebbe un'agitazione derivante dall'incertezza interiore; di conseguenza, i concetti di certezza e incertezza si collegano agli stati epistemici soggettivi degli individui e non agli stati del mondo esterno, poiché, in quest'ultimo, non esistono certezza o incertezza, ma solo fatti concreti. Pertanto, esistono sia un mondo interiore sia un mondo esterno che non si conformano ai principi di incertezza, bensì di probabilità.

Mary Poppins potrebbe sentirsi soggettivamente certa o incerta riguardo alla propria condizione, che potrebbe essere TMD o un disturbo neuropatico o neuromuscolare dell'OP: ciò avviene perché "l'incertezza" rappresenta uno stato epistemico soggettivo situato al di sotto della soglia della conoscenza e del credo, da cui origina il termine stesso.

Incertezza soggettiva

Il termine “soggettivo” può creare preoccupazione, in particolare tra coloro che cercano di applicare la scienza seguendo l'ideale di "oggettività", come comunemente inteso. È necessario, dunque, chiarire il significato di questo termine nel contesto attuale:

"Soggettivo" implica che la valutazione della probabilità varia in base allo stato informativo dell'individuo che la effettua.
"Soggettivo" non equivale ad arbitrario.

Quello che comunemente si intende per "oggettività", specialmente al di fuori dell'ambito scientifico, si verifica quando una comunità di soggetti razionali condivide lo stesso insieme di informazioni. Tuttavia, anche in tale contesto, sarebbe più corretto parlare di “intersoggettività”, ossia la condivisione di giudizi soggettivi all'interno di un gruppo.

In ambito clinico, dato che i pazienti raramente hanno una conoscenza avanzata della medicina, l'incertezza soggettiva assume un ruolo centrale. Affrontare l'incertezza ci spinge verso l'adozione di un approccio basato sulla probabilità.

Casualità

La casualità riflette l'assenza di una relazione definita e prevedibile tra causa ed effetto. La sfida di stabilire un legame diretto e inequivocabile tra la causa e il suo effetto rappresenta uno degli ostacoli principali nella formulazione di una diagnosi precisa.

In un contesto clinico, un fenomeno $A(x)$ (ad esempio, una malocclusione, un crossbite, un openbite, ecc...) può essere legato in maniera casuale a un altro fenomeno $B(x)$ (come la degenerazione ossea dell'ATM); quando esistono eccezioni per cui la proposizione logica $A(x)\rightarrow B(x)$ non risulta essere costantemente valida (sebbene lo sia nella maggior parte dei casi), si afferma che la relazione $A(x)\rightarrow B(x)$ non è universalmente vera, ma probabile.

«Stiamo passando da una condizione deterministica a una condizione stocastica.»

== Probabilità soggettiva e oggettiva ==

In questo capitolo, si riprendono alcuni concetti già esplorati nell'opera fondamentale di Kazem Sadegh-Zadeh, ^[3] che indaga la logica del linguaggio medico. I concetti vengono adattati al nostro studio di caso clinico su Mary Poppins, per avvicinare la nostra comprensione ai contesti odontoiatrici.

Si considerano probabili gli eventi casuali e quelli soggettivamente incerti; di conseguenza, la casualità e l'incertezza vengono interpretate come probabilità, che possono essere qualitative, comparative o quantitative.

Per illustrare meglio, facciamo riferimento all'esempio di Mary Poppins. Un medico, dopo aver esaminato i suoi sintomi, potrebbe affermare che:

Mary Poppins è probabilmente affetta da TMD (termine qualitativo).
Mary Poppins ha maggiori probabilità di soffrire di TMD rispetto a OP neuropatici (termine comparativo: numero di casi di TMD diagnosticati rispetto a _nOP).
La probabilità che Mary Poppins soffra di TMD è del 15% (termine quantitativo, basato sulla popolazione; un concetto che si ritrova nel teorema di Bayes).

Probabilità soggettiva

Nel contesto dell'incertezza soggettiva umana, i dati probabilistici — sia qualitativi, comparativi che quantitativi — possono essere interpretati dal clinico come espressione dell'incertezza soggettiva, consentendo una rappresentazione numerica degli "stati di convinzione".

Ad esempio, affermare che "la probabilità che Mary Poppins sia affetta da TMD è del 15%" equivale a dire "sono convinto al 15% che Mary Poppins soffra di TMD", indicando che il grado di convinzione corrisponde al grado di probabilità soggettiva.

Probabilità oggettiva

D'altro canto, gli eventi e i processi casuali non possono essere descritti mediante processi deterministici di tipo "se A, allora B". La statistica è utilizzata per quantificare la frequenza di associazione tra A e B, rappresentando le loro relazioni come gradi di probabilità che definiscono il concetto di probabilità oggettiva.

Con l'evolversi della medicina e l'aumento della tendenza a quantificare incertezza e casualità a partire dal XVIII secolo, il termine "probabilità" è divenuto un elemento fondamentale nel linguaggio, nella metodologia e nell'epistemologia medica. Purtroppo, la distinzione tra probabilità soggettiva e oggettiva non è sempre chiara in ambito medico, così come in altre discipline. Ciò nonostante, il contributo più significativo della teoria della probabilità alla medicina, in particolare nei concetti di eziologia, epidemiologia, diagnostica e terapia, risiede nella sua capacità di migliorare la nostra comprensione e rappresentazione della casualità biologica.

Analisi probabilistico-causale

Dalle premesse emerge che la diagnosi clinica viene effettuata tramite il metodo ipotetico-deduttivo, noto come DN^[4] (modello deduttivo-nomologico)^[5]. Tuttavia, questa rappresentazione non è realistica, in quanto le conoscenze mediche impiegate nel processo decisionale clinico raramente includono leggi deterministiche causali che consentono spiegazioni causali e, di conseguenza, la formulazione di diagnosi cliniche, soprattutto in ambito specialistico. Esaminiamo nuovamente il caso di Mary Poppins, tentando questa volta un approccio probabilistico-causale.

Prendiamo in considerazione un gruppo di $n$ individui, inclusi quelli che lamentano dolore orofacciale generalmente associato a degenerazione ossea dell'articolazione temporo-mandibolare. Tuttavia, potrebbero esistere altre cause apparentemente non correlate. È necessario tradurre matematicamente la "rilevanza" che queste incertezze causali rivestono nel determinare una diagnosi.

La rilevanza causale

Per affrontare questa questione, consideriamo il grado di rilevanza causale $(cr)$ di un evento $E_{1}$ rispetto a un evento $E_{2}$ , dove:

$E_{1}$ = pazienti con degenerazione ossea dell'articolazione temporo-mandibolare.
$E_{2}$ = pazienti che hanno riportato dolore orofacciale.
$E_{3}$ = pazienti senza degenerazione ossea dell'articolazione temporo-mandibolare.

La probabilità condizionata $P(A\mid B)$ è usata per calcolare la probabilità che l'evento $A$ si verifichi dato che l'evento $B$ si è già verificato.

La rilevanza causale $cr$ del campione $E_{1}$ di pazienti si determina come:

$cr=P(E_{2}\mid E_{1})-P(E_{2}\mid E_{3})$

dove:

$P(E_{2}\mid E_{1})$ indica la probabilità che alcune persone (tra $n$ considerate) soffrano di dolore orofacciale causato dalla degenerazione ossea dell'articolazione temporo-mandibolare,

mentre

$P(E_{2}\mid E_{3})$ indica la probabilità che altre persone (sempre tra $n$ considerate) soffrano di dolore orofacciale causato da altri fattori non legati alla degenerazione ossea dell'articolazione temporo-mandibolare.

Poiché tutte le probabilità suggeriscono che $P(A\mid B)$ , il valore di $cr$ sarà compreso tra $-1$ e $1$ . I significati attribuibili a questo valore sono:

$cr=1$ indica che l'unica causa di dolore orofacciale è la degenerazione ossea dell'ATM,

$cr=-1$ indica che la degenerazione ossea dell'ATM non è mai la causa del dolore orofacciale, ma sempre qualcos'altro,

$cr=0$ indica che la probabilità che il dolore orofacciale sia causato dalla degenerazione ossea dell'ATM o da altri fattori è esattamente la stessa,

e, nei casi intermedi, più realistici:

$cr>0$ indica che è più probabile che la degenerazione ossea dell'ATM sia la causa del dolore orofacciale,

$cr<0$ indica che è più probabile che la causa del dolore orofacciale non sia la degenerazione ossea dell'ATM.

2° Approccio clinico

Figura 1: Paziente che riferisce "Dolore orofacciale emilaterale destro"
Figura 2: Stratigrafia dell'ATM del paziente che mostra segni di appiattimento condilare e osteofiti
Figura 3: Tomografia computerizzata dell'ATM
Figura 4: Assiografia del paziente che mostra un appiattimento del pattern masticatorio sul condilo destro
Figura 5: Schema interferente EMG. Tracce superiori sovrapposte corrispondenti al massetere destro, in basso al massetere sinistro.

Sia quindi $P(D)$ la probabilità di identificare, nel nostro campione di $n$ persone, individui che presentano gli elementi appartenenti all'insieme specificato $D={\delta _{1},\delta _{2},...,\delta _{n}}$ . Per utilizzare le informazioni fornite da questo dataset, viene introdotto il concetto di partizione di rilevanza causale:

La partizione della rilevanza causale

Essendo $n$ il numero di persone su cui dobbiamo condurre le analisi, se dividiamo questo gruppo, in base a determinate condizioni come spiegato di seguito, in $k$ sottoinsiemi $C_{i}$ con $i=1,2,\dots ,k$ , viene creato un cluster chiamato "set di partizioni" $\pi$ .

$\pi ={C_{1},C_{2},\dots ,C_{k}}\qquad \qquad {\text{con}}\qquad \qquad C_{i}\subset n,$

dove il simbolismo $C_{i}\subset n$ indica che la sottoclasse $C_{i}$ è contenuta nel numero $n$ .

Per poter definire la partizione $\pi$ come partizione di rilevanza causale, deve possedere queste proprietà:

Per ogni sottoclasse $C_{i}$ , la condizione deve essere che $rc=P(D\mid C_{i})-P(D)\neq 0,$ ovvero la probabilità di trovare nel sottogruppo $C_{i}$ una persona che presenti i sintomi, i segni clinici e gli elementi appartenenti all'insieme $D={\delta _{1},\delta _{2},...,\delta _{n}}$ . Una partizione causalmente rilevante di questo tipo viene definita omogenea. Ogni sottoinsieme $C_{i}$ deve essere 'elementare', cioè non deve essere ulteriormente suddiviso in altri sottoinsiemi, poiché, in tal caso, non avrebbero rilevanza causale.

Assumiamo ora, ad esempio, che il campione di popolazione $n$ , a cui appartiene la nostra paziente Mary Poppins, sia una categoria di soggetti dai 20 ai 70 anni. Supponiamo inoltre che in questa popolazione ci siano individui che presentano gli elementi appartenenti al set di dati $D={\delta _{1},.....,\delta _{n}}$ , corrispondenti alle prove di laboratorio menzionate e descritte in 'La logica del linguaggio classico'.

Supponiamo che in un campione di 10.000 soggetti dai 20 ai 70 anni abbiamo un'incidenza di 30 soggetti $p(D)=0.003$ che presentano i segni clinici $\delta _{1}$ e $\delta _{4}$ . Abbiamo scelto di utilizzare questi dati per dimostrare il processo probabilistico perché in letteratura i dati relativi ai segni e sintomi clinici per i disturbi temporo-mandibolari variano ampiamente e presentano un'incidenza che riteniamo eccessivamente alta.

^[6]^[7]^[8]^[9]^[10]^[11]

Un esempio di una partizione con presunta probabilità in cui la degenerazione dell'ATM (Deg.TMJ) si verifica in combinazione con i disturbi temporomandibolari (TMD) sarebbe il seguente:


$P(D\|Deg.TMJ\cap TMDs)=0.95\qquad \qquad \;$	dove	$\mathbb {C} _{1}\equiv Deg.TMJ\cap TMDs$
$P(D\|Deg.TMJ\cap noTMDs)=0.3\qquad \qquad \quad$	dove	$C_{2}\equiv Deg.TMJ\cap noTMDs$
$P(D\|noDeg.TMJ\cap TMDs)=0.199\qquad \qquad \;$	dove	$C_{3}\equiv noDeg.TMJ\cap TMDs$
$P(D\|noDeg.TMJ\cap noTMDs)=0.001\qquad \qquad \;$	dove	$C_{4}\equiv noDeg.TMJ\cap noTMDs$

«Una partizione omogenea fornisce ciò che siamo abituati a chiamare Diagnosi Differenziale.»

Situazioni cliniche

Queste probabilità condizionali dimostrano che ciascuna delle quattro sottoclassi della partizione è causalmente rilevante per i dati del paziente $D={\delta _{1},.....\delta _{n}}$ nel campione di popolazione $PO$ . Date le suddette partizioni della classe di riferimento, abbiamo le seguenti situazioni cliniche:

$\mathbb {C} _{1}\equiv$ Mary Poppins $\in$ degenerazione dell'articolazione temporo-mandibolare $\cap$ Disturbi temporo-mandibolari
$\mathbb {C} _{2}\equiv$ Mary Poppins $\in$ degenerazione dell'articolazione temporo-mandibolare $\cap$ no Disturbi temporo-mandibolari
$\mathbb {C} _{3}\equiv$ Mary Poppins $\in$ no degenerazione dell'articolazione temporo-mandibolare $\cap$ Disturbi temporo-mandibolari
$\mathbb {C} _{4}\equiv$ Mary Poppins $\in$ no degenerazione dell'articolazione temporo-mandibolare $\cap$ no Disturbi temporo-mandibolari Per arrivare alla diagnosi finale sopra menzionata, abbiamo condotto un'analisi probabilistico-causale dello stato di salute di Mary Poppins, i cui dati iniziali erano $D={\delta _{1},.....\delta _{n}}$ .

In generale, possiamo fare riferimento a un processo logico in cui esaminiamo i seguenti elementi:

Un individuo: $a$
Il suo set di dati iniziale $D={\delta _{1},.....\delta _{n}}$
Un campione di popolazione $n$ a cui appartiene
Una probabilità di base $P(D)=0.003$

A questo punto, dovremmo introdurre argomentazioni troppo specialistiche che distoglierebbero il lettore dall'argomento principale, ma che hanno un'elevata importanza epistemica. Pertanto, cercheremo di estrarre il filo logico più semplice descritto nel concetto Analysandum/Analysans.

Nell'analisi probabilistico-causale di $D={\delta _{1},.....\delta _{n}}$ , si distinguono un paio delle seguenti forme logiche (Analysandum/Analysans):

Analysandum $=\{P(D),a\}$ : è una forma logica che contiene due parametri: la probabilità $P(D)$ di selezionare una persona che presenta i sintomi e gli elementi appartenenti all'insieme $D=\{\delta _{1},\delta _{2},...,\delta _{n}\}$ e il generico individuo $a$ incline a quei sintomi.

Analysan $=\{\pi ,a,KB\}$ : è una forma logica che contiene tre parametri: la partizione $\pi$ , il generico individuo $a$ appartenente al campione di popolazione $n$ e la $KB$ (Conoscenza di base), che comprende un insieme di affermazioni di probabilità condizionata superiori a $n>1$ .

Ad esempio, si può concludere che la diagnosi definitiva sia la seguente:

$P(D|Deg.TMJ\cap TMDs)=0.95$

significa che la nostra Mary Poppins ha il 95% di probabilità di soffrire di Disturbi Temporo-Mandibolari (TMD), in quanto presenta una degenerazione dell'articolazione temporo-mandibolare oltre ad altri indicatori positivi inclusi nel set di dati $D={\delta _{1},.....\delta _{n}}$ .

Considerazioni finali

Abbiamo percorso una strada lunga e complessa per comprendere meglio la complessità che i professionisti affrontano di fronte all'enorme responsabilità etica di formulare una diagnosi. Questa sfida diventa ancora più ardua quando si richiede di essere meticolosi e attenti nel procedere con una diagnosi differenziale.

Ci addentriamo ora in un tema delicato, legato agli aspetti epistemologici, che è stato introdotto nella "Introduzione". Ci riferiamo a:

Interdisciplinarità: Nella politica scientifica è ampiamente accettato che la soluzione dei problemi basati sulla scienza necessiti di ricerca interdisciplinare (IDR), come evidenziato dal programma Horizon 2020 dell'UE.^[12] Un recente studio si focalizza sulle difficoltà cognitive ed epistemiche che i ricercatori incontrano nell'IDR. Si sostiene che il declino dell'interesse filosofico per l'epistemologia della ricerca interdisciplinare derivi da un paradigma filosofico chiamato "Physics Paradigm of Science", che limita il riconoscimento dei significativi cambiamenti nell'IDR sia nella filosofia della scienza che nella pratica di ricerca. Il paradigma filosofico alternativo proposto, denominato "Paradigma ingegneristico della scienza", introduce ipotesi filosofiche alternative riguardo lo scopo della scienza, la natura della conoscenza, i criteri epistemici e pragmatici per l'accettazione della conoscenza, e il ruolo degli strumenti tecnologici. Di conseguenza, i ricercatori scientifici richiedono i cosiddetti "scaffolds metacognitivi" per assistere nell'analisi e nella ricostruzione del modo in cui la "conoscenza" è costruita nelle varie discipline.^[13]^[14]

Questo concetto è collegato alla discussione precedente, in cui si sottolinea l'importanza per il professionista di essere consapevole della propria 'Incertezza Soggettiva', derivante dall'utilizzo di un linguaggio logico classico 'malato o sano', e dellIncertezza Oggettiva', originata da un linguaggio logico probabilistico 'probabilmente malato o probabilmente sano'. Dimostrare questa affermazione non è complesso: l'incertezza in questione emerge dal fatto che gli elementi, le affermazioni, i dati, le classi e le sottoclassi menzionati, che formano la struttura della logica del linguaggio probabilistico, Analysandum $={P(D),a}$ e Analysan $={\pi ,a,KB}$ , sono concetti che trovano applicazione in ambiti specifici, in questo caso, nell'ambito odontoiatrico, dove l'elemento $KB$ nel processo rappresenta chiaramente una "conoscenza di base" specifica per il settore odontoiatrico.

Questa conclusione confermata dal dentista è stata la seguente:

$P(D|Deg.TMJ\cap TMDs)=0.95$

In altre parole, sono fermamente convinto che Mary Poppins soffra di TMD con una probabilità del 95%, a causa della degenerazione dell'articolazione temporo-mandibolare e della conferma dei dati $D={\delta _{1},\dots \delta _{n}}$ . Tuttavia, emerge un'inattesa complessità quando, improvvisamente, un ricercatore introduce l'utilizzo di 'scaffold metacognitivi'^[15] per facilitare l'analisi e la ricostruzione di come la 'conoscenza' viene integrata tra le diverse discipline, sollecitando il dentista a rispondere alla seguente domanda:

«Esiste un altro mondo o contesto, parallelo al tuo, dove ci sono dati che non conosci?»

E poi, rafforza la richiesta suggerendo di: sottoporre Mary Poppins a specifici test elettrofisiologici trigeminali, classificandoli come già fatto in precedenza per il set di dati $D={\delta _{1},\dots \delta _{n}}$ , e generando un nuovo insieme di dati che comprende un numero $m$ di dati sconosciuti $C={\gamma _{1},\dots \gamma _{m}}$ (che non appartengono esclusivamente all'ambito dentale), formando così un nuovo insieme denominato $S_{unknown}=D+C={\delta _{1},\dots ,\delta _{n},\gamma _{1},\dots ,\gamma _{m}}$ , così chiamato per la presenza di dati non familiari al contesto odontoiatrico.

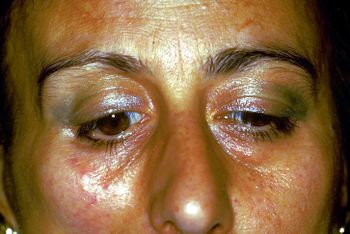
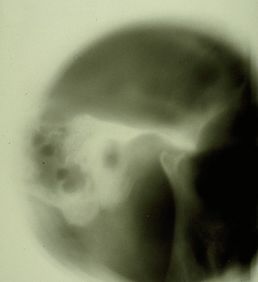
$\delta _{1}=$ Referto radiologico positivo dell'ATM visualizzato in Figura 2

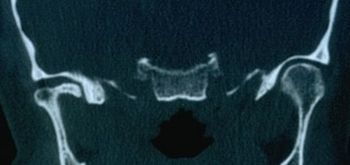
$\delta _{2}=$ Referto radiologico positivo dell'ATM mostrato in Figura 3

$\delta _{3}=$ Referto assiografico che evidenzia tracce condilari positive in Figura 4

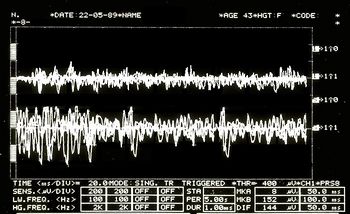
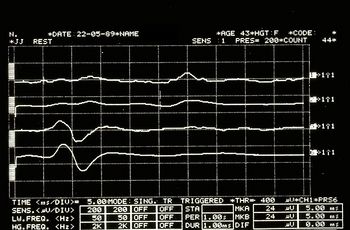
$\delta _{4}=$ Pattern di interferenza EMG asimmetrico rappresentato in Figura 5

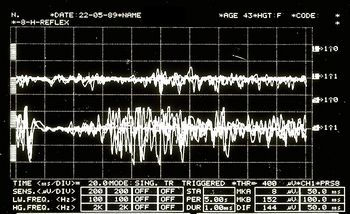
$\gamma _{1}=$ Jaw jerk illustrato in Figura 6

$\gamma _{2}=$ Periodo silente meccanico masseterino presentato in Figura 7

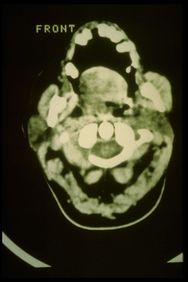
$\gamma _{3}=$ CT del muscolo massetere destro esposto in Figura 8

3° Approccio clinico

Figura 1: Paziente che riferisce "Dolore orofacciale nell'emilato facciale destro)
Figura 2: Stratigrafia dell'ATM del paziente che mostra segni di appiattimento condilare e osteofiti
Figura 3: Tomografia computerizzata dell'ATM
Figura 4: Assiografia del paziente che mostra un appiattimento del pattern masticatorio sul condilo destro
Figura 5: Schema interferente EMG. Tracce superiori sovrapposte corrispondenti al massetere destro, in basso al massetere sinistro.
Figura 6: Jaw jerk rilevato elettrofisiologicamente sui masseteri destro (tracce superiori) e sinistro (tracce inferiori)
Figura 7: Periodo di silenzio meccanico rilevato elettrofisiologicamente sui masseteri di destra (tracce sovrapposte superiori) e di sinistra (tracce sovrapposte inferiori)
Figura 8: TC assiale del massiccio facciale in cui è presente una marcata ipertrofia del massetere destro

ICosì facendo, si è evidenziato che, inevitabilmente,

«la logica del linguaggio medico si fonda in larga misura su dati provenienti da un mondo o contesto specifico, ovvero un ambito specialistico, all'interno del quale i confini delimitanti tale conoscenza non consentono l'espansione verso contesti paralleli.»

Nel sondare i confini di questo ambito specialistico, si intende avvicinarsi a un'area contigua, denominata "zona fuzzy" o "logica fuzzy". Quest'ultima sarà oggetto di discussione nel capitolo successivo.

«...sembra che, anche adottando una logica linguistica probabilistica, non si possa giungere a una diagnosi precisa. Di conseguenza, emerge la necessità di esplorare la Fuzzy Logic Language.»

Bibliography & references

↑ Vázquez-Delgado E, Cascos-Romero J, Gay-Escoda C, «Myofascial pain associated with trigger points: a literature review. Part 2: Differential diagnosis and treatment», in Med Oral Patol Oral Cir Bucal, 2010».
PMID:20173729
DOI:10.4317/medoral.15.e639
↑ Thoppay J, Desai B, «Oral burning: Local and systemic connections for a patient-centric approach», in EPMA J, 2019».
PMID:30984309 - PMCID:PMC6459460
DOI:10.1007/s13167-018-0157-3
↑ Sadegh-Zadeh Kazem, «Handbook of Analytic Philosophy of Medicine», Springer, 2012, Dordrecht».
ISBN: 978-94-007-2259-0
DOI:10.1007/978-94-007-2260-6
↑ Sarkar S, «Nagel on Reduction», in Stud Hist Philos Sci, 2015».
PMID:26386529
DOI:10.1016/j.shpsa.2015.05.006
↑ DN model of scientific explanation, also known as Hempel's model, Hempel–Oppenheim model, Popper–Hempel model, or covering law model
↑ Pantoja LLQ, De Toledo IP, Pupo YM, Porporatti AL, De Luca Canto G, Zwir LF, Guerra ENS, «Prevalence of degenerative joint disease of the temporomandibular joint: a systematic review», in Clin Oral Investig, 2019».
PMID:30311063
DOI:10.1007/s00784-018-2664-y
↑ De Toledo IP, Stefani FM, Porporatti AL, Mezzomo LA, Peres MA, Flores-Mir C, De Luca Canto G, «Prevalence of otologic signs and symptoms in adult patients with temporomandibular disorders: a systematic review and meta-analysis», in Clin Oral Investig, 2017».
PMID:27511214
DOI:10.1007/s00784-016-1926-9
↑ Bonotto D, Penteado CA, Namba EL, Cunali PA, Rached RN, Azevedo-Alanis LR, «Prevalence of temporomandibular disorders in rugby players», in Gen Dent».
PMID:31355769
↑ da Silva CG, Pachêco-Pereira C, Porporatti AL, Savi MG, Peres MA, Flores-Mir C, De Luca Canto G, «Prevalence of clinical signs of intra-articular temporomandibular disorders in children and adolescents: A systematic review and meta-analysis», in Am Dent Assoc, 2016». - PMCID:26552334
DOI:10.1016/j.adaj.2015.07.017
↑ Gauer RL, Semidey MJ, «Diagnosis and treatment of temporomandibular disorders», in Am Fam Physician, 2015».
PMID:25822556
↑ Kohlmann T, «Epidemiology of orofacial pain», in Schmerz, 2002».
PMID:12235497
DOI:10.1007/s004820200000
↑ European Union, Horizon 2020
↑ Boon M, Van Baalen S, «Epistemology for interdisciplinary research - shifting philosophical paradigms of science», in Eur J Philos Sci, 2019».
DOI:10.1007/s13194-018-0242-4 9(1):16.
↑ Boon M, «An engineering paradigm in the biomedical sciences: Knowledge as epistemic tool», in Prog Biophys Mol Biol, 2017».
DOI:10.1016/j.pbiomolbio.2017.04.001
↑ Boon M, Van Baalen S, «Epistemology for interdisciplinary research - shifting philosophical paradigms of science», in Eur J Philos Sci, 2019».
PMID:30873248 - PMCID:PMC6383598
DOI:10.1007/s13194-018-0242-4

This is an Open Access resource!

Masticationpedia is a charity, a not-for-profit organization operating in dentistry medical research,
particularly focusing on the field of the neurophysiology of the masticatory system

Bibliography & references

[1] Vázquez-Delgado E, Cascos-Romero J, Gay-Escoda C, «Myofascial pain associated with trigger points: a literature review. Part 2: Differential diagnosis and treatment», in Med Oral Patol Oral Cir Bucal, 2010».
PMID:20173729
DOI:10.4317/medoral.15.e639

[2] Thoppay J, Desai B, «Oral burning: Local and systemic connections for a patient-centric approach», in EPMA J, 2019».
PMID:30984309 - PMCID:PMC6459460
DOI:10.1007/s13167-018-0157-3

[3] Sadegh-Zadeh Kazem, «Handbook of Analytic Philosophy of Medicine», Springer, 2012, Dordrecht».
ISBN: 978-94-007-2259-0
DOI:10.1007/978-94-007-2260-6

[:1-4] Sarkar S, «Nagel on Reduction», in Stud Hist Philos Sci, 2015».
PMID:26386529
DOI:10.1016/j.shpsa.2015.05.006

[5] DN model of scientific explanation, also known as Hempel's model, Hempel–Oppenheim model, Popper–Hempel model, or covering law model

[:2-6] Pantoja LLQ, De Toledo IP, Pupo YM, Porporatti AL, De Luca Canto G, Zwir LF, Guerra ENS, «Prevalence of degenerative joint disease of the temporomandibular joint: a systematic review», in Clin Oral Investig, 2019».
PMID:30311063
DOI:10.1007/s00784-018-2664-y

[:3-7] De Toledo IP, Stefani FM, Porporatti AL, Mezzomo LA, Peres MA, Flores-Mir C, De Luca Canto G, «Prevalence of otologic signs and symptoms in adult patients with temporomandibular disorders: a systematic review and meta-analysis», in Clin Oral Investig, 2017».
PMID:27511214
DOI:10.1007/s00784-016-1926-9

[:4-8] Bonotto D, Penteado CA, Namba EL, Cunali PA, Rached RN, Azevedo-Alanis LR, «Prevalence of temporomandibular disorders in rugby players», in Gen Dent».
PMID:31355769

[:5-9] Silva CG, Pachêco-Pereira C, Porporatti AL, Savi MG, Peres MA, Flores-Mir C, De Luca Canto G, «Prevalence of clinical signs of intra-articular temporomandibular disorders in children and adolescents: A systematic review and meta-analysis», in Am Dent Assoc, 2016». - PMCID:26552334
DOI:10.1016/j.adaj.2015.07.017

[:6-10] Gauer RL, Semidey MJ, «Diagnosis and treatment of temporomandibular disorders», in Am Fam Physician, 2015».
PMID:25822556

[:7-11] Kohlmann T, «Epidemiology of orofacial pain», in Schmerz, 2002».
PMID:12235497
DOI:10.1007/s004820200000

[12] European Union, Horizon 2020

[:0-13] Boon M, Van Baalen S, «Epistemology for interdisciplinary research - shifting philosophical paradigms of science», in Eur J Philos Sci, 2019».
DOI:10.1007/s13194-018-0242-4 9(1):16.

[14] Boon M, «An engineering paradigm in the biomedical sciences: Knowledge as epistemic tool», in Prog Biophys Mol Biol, 2017».
DOI:10.1016/j.pbiomolbio.2017.04.001

[15] Boon M, Van Baalen S, «Epistemology for interdisciplinary research - shifting philosophical paradigms of science», in Eur J Philos Sci, 2019».
PMID:30873248 - PMCID:PMC6383598
DOI:10.1007/s13194-018-0242-4

This is an Open Access resource!

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]