Explorer l'électroencéphalographie avec un modèle inspiré de la mécanique quantique

Free resource

Exploring electroencephalography with a model inspired by quantum mechanics

Free resource by Nicholas J. M. Popiel  · Colin Metrow · Geofrey Laforge  · Adrian M. Owen · Bobby Stojanoski  · Andrea Soddu

Nicholas J. M. Popiel,^1,2 Colin Metrow,¹ Geoffrey Laforge,³ Adrian M. Owen,^3,4,5 Bobby Stojanoski,^#4,6 and Andrea Soddu^{#1,3 1}The Department of Physics and Astronomy, The University of Western Ontario, London, ON N6A 5B7 Canada

²Cavendish Laboratory, University of Cambridge, Cambridge, CB3 0HE UK

³The Brain and Mind Institute, The University of Western Ontario, London, ON N6A 5B7 Canada

⁴The Department of Psychology, The University of Western Ontario, London, ON N6A 5B7 Canada

⁵The Department of Physiology and Pharmacology, The University of Western Ontario, London, ON N6A 5B7 Canada

⁶Faculty of Social Science and Humanities, University of Ontario Institute of Technology, 2000 Simcoe Street North, Oshawa, ON L1H 7K4 Canada

Extract

Un problème en suspens dans les neurosciences cognitives concerne la façon dont le cerveau est organisé dans différentes conditions. Par exemple, pendant l'état de repos, le cerveau peut être regroupé en réseaux fiables et reproductibles (par exemple, réseaux sensoriels, par défaut, exécutifs). Fait intéressant, les mêmes réseaux émergent pendant les conditions actives en réponse à diverses tâches. Si des modèles similaires d'activité neuronale ont été trouvés dans diverses conditions, et donc, différents processus sous-jacents et expériences de l'environnement, le cerveau est-il organisé par un principe organisationnel fondamental ? Pour tester cela, nous avons appliqué des formalismes mathématiques empruntés aux mécanismes quantiques pour modéliser les données de l'électroencéphalogramme (EEG). Nous avons découvert une tendance à ce que les signaux EEG soient localisés dans les régions antérieures du cerveau pendant le « repos » et distribués plus uniformément lorsqu'ils sont engagés dans une tâche (c'est-à-dire regarder un film). De plus, nous avons trouvé des valeurs analogues au principe d'incertitude de Heisenberg, suggérant une architecture sous-jacente commune de l'activité cérébrale humaine dans des conditions de repos et de tâche. Cette architecture sous-jacente se manifeste dans la nouvelle constante$K_{brain}$, qui est extrait de l'état du cerveau avec le moins d'incertitude. Nous voudrions déclarer que nous utilisons les mathématiques de la mécanique quantique, mais sans prétendre que le cerveau se comporte comme un objet quantique.

Subject terms: Computational science, Quantum mechanics

Introduction

Une question importante mais en suspens dans les neurosciences cognitives contemporaines est de comprendre les propriétés organisationnelles de l'activité neuronale. Par exemple, existe-t-il une structure fondamentale de l'activité cérébrale neuronale des modèles spatio-temporels dans différentes conditions ? Une approche courante utilisée pour répondre à cette question consiste à examiner le cerveau au « repos ». Des mesures telles que la connectivité fonctionnelle, l'analyse des composants indépendants et les métriques théoriques des graphes ont été appliquées aux données enregistrées à l'aide de différentes techniques d'imagerie (par exemple, l'imagerie par résonance magnétique fonctionnelle (IRMf) et l'électroencéphalographie (EEG)), pour regrouper les zones cérébrales qui présentent des modèles d'activité similaires . De nombreuses études ont montré que l'activité cérébrale pendant le "repos" peut être regroupée en réseaux distincts à travers; tels que les réseaux sensoriels (visuels et auditifs), en mode par défaut, exécutifs, saillants et attentionnels (ventraux et dorsaux) qui ont été reproduits de manière fiable sur des milliers de participants et sont prédictifs de mesures phénotypiques telles que la cognition et les diagnostics cliniques. Ces résultats suggèrent que ces réseaux peuvent être un aspect intrinsèque de l'activité neuronale.

Modèles et mathématiques

En effet, le même ensemble de schémas structurés d'activité neuronale a été trouvé lors d'états "actifs", par exemple lors de l'accomplissement de différentes tâches. Par exemple, il existe un degré élevé de correspondance entre les réseaux extraits au repos et ceux extraits lors de tâches mesurant les capacités sensorimotrices et cognitives de niveau supérieur (c'est-à-dire la mémoire de travail). Même architecture de réseau que celle observée dans le cerveau au repos. La correspondance entre les réseaux basés sur la tâche et le repos est si forte que l'activité du réseau IRMf basée sur la tâche peut être prédite à partir de l'état de repos, et les paires de réseaux repos-tâche peuvent être identifiées au niveau individuel. Ensemble, ces résultats suggèrent que les schémas d'activité cérébrale basés sur le repos et les tâches partagent probablement une architecture neuronale sous-jacente similaire, malgré des expériences et des processus cognitifs distincts.

Il existe cependant des différences importantes entre les modèles d'activité cérébrale suscités pendant le repos et les paradigmes basés sur les tâches, et l'ensemble des expériences et des processus cognitifs associés à chacun. Par exemple, la présence ou l'absence d'une tâche s'accompagne d'une augmentation de la variabilité à différentes échelles, y compris les changements de taux de déclenchement neuronal dans les potentiels de champ, la variation du niveau d'oxygène dans le sang IRMf (signal BOLD) et dans les bandes de fréquences EEG. En outre, grâce au courant continu transcrânien stimulation (tDCS) il a été démontré que la stimulation du lobe frontal augmente la propension à l'errance mentale. Il est important de noter que ces différences sont associées à des changements dans les propriétés de l'activité neuronale, mais pas à des changements dans l'architecture neuronale sous-jacente.

Existe-t-il un moyen d'identifier l'architecture neuronale partagée sous-jacente aux processus cognitifs associés aux états de repos et d'activité tout en quantifiant la façon dont ces processus divergent de cette architecture partagée de l'activité neuronale ? Dans cet article, nous avons appliqué des méthodes mathématiques analogues à celles de la mécanique quantique et le concept d'espace de phase à l'EEG enregistré pendant le repos et l'observation de films pour extraire les propriétés spatiales et transitionnelles de l'activité neuronale dynamique. La mécanique quantique a été développée pour décrire la dynamique du monde subatomique en termes d'amplitudes de probabilité et de densités d'états. Les systèmes quantiques (dans la formulation de Schrödinger de la mécanique quantique) sont décrits par des fonctions d'onde qui correspondent à une distribution de probabilité conduisant à la perte du déterminisme local et au principe d'incertitude de Heisenberg (pour un aperçu / introduction au sujet, voir).

Ce principe d'incertitude place un élément fondamental limite sur l'emplacement et l'impulsion d'une particule ponctuelle. Essentiellement, si la position d'une particule est connue, il existe une incertitude sous-jacente dans son impulsion (on ne peut pas dire avec précision à quelle vitesse elle va) et vice versa. En plus de la adaptation de l'approche de la fonction d'onde à la mécanique quantique dans cet article, nous avons également utilisé un modèle d'espace de phase.L'espace de phase est un outil largement utilisé dans l'étude des systèmes dynamiques, où les variables de position sont appariées avec leurs moments conjugués, ce qui établit un espace multidimensionnel qui décrit toutes les configurations possibles du système donné. Cet espace couvre toute la gamme des états dans lesquels un système peut exister, chacun point (dans cet hyper-espace) représente un seul état du système. L'espace de phase et ses formalismes assortis sont un concept classique, et nous l'utilisons simplement comme un autre outil pour analyser les données EEG. Ici, les méthodes mathématiques de la mécanique quantique sont appliquées aux données EEG pour extraire un proxy à l'espace des phases. Cette approche quasi-quantique génère naturellement les concepts de position « moyenne », de moment « moyen » et aboutit à un principe d'incertitude de Heisenberg analogue.

Dans cet article, nous postulons qu'en utilisant des outils mathématiques tirés de la mécanique quantique, un modèle sous-jacent représentatif de la tâche et de l'activité cérébrale au repos peut être réalisé, dans lequel les différences entre les conditions sont apparentes, mais aboutissent à une valeur constante indépendante de la tâche. Il est important de noter que nous ne prétendons pas que le cerveau se comporte comme un objet quantique comme certains le croient.

Au lieu de cela, nous avons utilisé certains des outils analytiques de la formulation de Schrodinger de la mécanique quantique au cerveau dans le but d'acquérir de nouvelles connaissances sur la dynamique cérébrale au repos et basée sur les tâches. Non seulement la conception de ce modèle pose des questions sur les fonctions du cerveau, mais elle fournit également une nouvelle approche pour analyser la myriade de données disponibles en neurosciences.

Résultats

Dans cet article, nous avons adapté les amplitudes de probabilité de la mécanique quantique pour définir de nouvelles métriques pour l'examen des données EEG - la "position moyenne" et "l'impulsion moyenne" du signal EEG. Ceux-ci ont été construits à partir de notre définition des «états cérébraux» basée sur le modèle quasi-quantique. Cela nous a permis de déterminer la fréquence à laquelle des régions cérébrales uniques sont entrées par la pseudo-fonction d'onde, ainsi que d'explorer l'espace de phase à valeur moyenne. Enfin, une relation d'incertitude analogue à celle de la mécanique quantique a été établie, avec la dérivation mathématique complète décrite dans les méthodes.

Valeurs moyennes

La «position moyenne» des données EEG a d'abord été extraite en effectuant une transformée de Hilbert des cours de temps prétraités, puis en appliquant une contrainte de normalisation. Typiquement, les données transformées de Hilbert sont utilisées pour générer une métrique de dispersion de puissance ou pour extraire la phase du signal. Au lieu de cela, nous avons imposé une nouvelle condition de normalisation, créant ainsi une analogie avec les fonctions d'onde de la mécanique quantique. En désignant le cours du temps transformé de Hilbert de la $j$ème électrode par $\Psi _{j}$, cela équivaut à

$\Psi _{j}(t)=A_{j}(t)\exp(i\theta _{j}(t))$

$(1)$

Avec $i={\sqrt {-1}}$. Nous avons alors imposé la condition de normalisation,

${\hat {\Psi }}_{j}(t)={\frac {\Psi _{j}(t)}{\sqrt {\sum _{j=1}^{92}|\Psi _{j}|^{2}}}}$

$(2)$

La sommation s'étend à 92, correspondant aux 92 électrodes sélectionnées parmi les 129 d'origine sur le capuchon (canaux retirés du visage et du cou pour cette analyse). Cette contrainte de normalisation nous a permis de définir la probabilité au temps $t$ de la $j$ $j$ème électrode comme

$P_{j}(t)={\hat {\Psi }}_{j}^{*}(t)\times {\hat {\Psi }}_{j}(t)$

$(3)$

Avec le * désignant la conjugaison complexe. Nous pouvons alors décrire chaque instant dans le temps comme un « état du cerveau » entièrement décrit (dans le contexte de ce modèle) par la « fonction d'onde ». Cet «état cérébral» spécifie de manière unique le signal EEG, et donc la dynamique d'intérêt, à chaque instant. En utilisant cette définition de la probabilité, nous avons défini deux quantités moyennes d'intérêt. La position moyenne et la quantité de mouvement sont données explicitement par,

$\langle x(t)\rangle =\sum _{j=1}^{92}x_{j}P_{j}(t)$ $\langle p_{x}(t)\rangle =m{d \over dt}\langle x(t)\rangle =m\sum _{j=1}^{92}x_{j}{d \over dt}P_{j}(t)$

$(4)$

De même pour $y$.

En pratique

Ces deux équations sont la façon dont nous créons nos analogues mécaniques quasi-quantiques. La deuxième équation est une extension du théorème d'Ehrenfest, reliant la quantité de mouvement moyenne d'une particule à la dérivée temporelle de sa position moyenne. Où nous avons supposé un hamiltonien avec seulement un potentiel spatialement dépendant. A noter que les positions étant fixes dans l'espace (positions des électrodes) seule la probabilité change dans le temps. Tout au long de cet article, la masse $m$ a été considérée comme égale à l'unité pour les impulsions $x$ et $y$. Chacune des 92 électrodes a été projetée sur le plan horizontal, ainsi le $j$ ème électrode a été décrite par un seul point $(x_{j},y_{j})$.

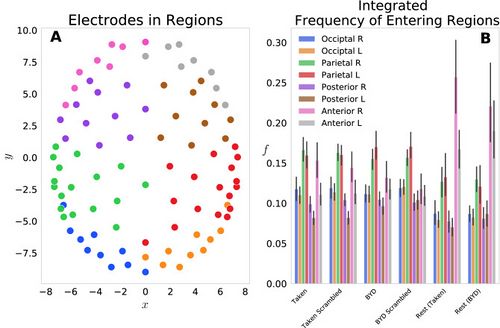
Nous avons d'abord examiné ce modèle en regroupant les 92 électrodes en huit régions sur le cuir chevelu : Antérieur G/D, Postérieur G/D, Pariétal G/D, Occipital G/D et les probabilités de chaque électrode dans la région ont été additionnées pour donner un probabilité au niveau de la région. La figure 1A montre les emplacements $(x_{j},y_{j})$ de chaque électrode, avec différentes couleurs représentant chacun des huit groupes. La figure 1B affiche la fréquence d'entrée dans chaque région, regroupée par les quatre conditions de tâche et les deux conditions de repos. Cela reflète le décompte normalisé des probabilités régionales intégrées dans le temps. Nous avons constaté que chaque région antérieure était pénétrée plus fréquemment au repos que lorsque les sujets étaient engagés dans l'un ou l'autre des films. Plus précisément, les régions antérieures gauche et droite présentaient un changement de stimulus significatif, avec $P<0.001$ (ajustement de Tukey) pour Taken Rest—Taken, Taken Rest—Taken Scrambled, BYD Rest—BYD et BYD Rest—BYD Scrambled. Ceci est conforme aux découvertes d'Axelrod et de ses collègues qui ont montré que l'activation dans la région frontale était associée à l'errance mentale.

Nous avons constaté une suppression de la fréquence dans les régions postérieures et une augmentation de la fréquence antérieure au repos par rapport aux conditions stimulées, ce qui est cohérent avec les études IRMf montrant une activation accrue dans le cortex cingulaire postérieur et le cortex préfrontal médial pendant le repos.

Ainsi, suggérant que notre modèle capture la tendance frontale associée à l'activité cérébrale au repos.

Figure 1 : (A) Emplacements des électrodes pour chacune des 92 électrodes sur le capuchon de tête de Electrical Geodesics Inc. Les électrodes ont été projetées sur un plan horizontal avec le nez dans la direction y positive. Les électrodes ont été codées par couleur pour afficher les éléments constitutifs des 8 groupes pour l'analyse de fréquence, à savoir, occipital gauche (bleu)/droit (orange), pariétal gauche (vert)/droit (rouge), postérieur gauche (violet)/ droite (marron) et antérieure gauche (rose)/droite (gris). (B) Des histogrammes représentant la fréquence d'entrée dans chaque région fG sont affichés pour les six conditions testées. Un changement significatif dans le stimulus est présent entre chacune des régions antérieures gauche et droite lors de la comparaison du repos pré-stimulus et de l'état stimulé respectif (P < 0,001, Tukey ajusté.). Les barres d'erreur affichent l'intervalle de confiance de 1 écart type.

Espace des phases

Nous avons également exploré l'espace des phases de valeur moyenne de ce système. L'espace de phase pour chaque sujet a été tracé comme la position et l'impulsion moyennes le long de la direction $x$, $(\langle x(t)\rangle ,\langle p_{x}(t)\rangle )$ou comme la position et l'impulsion moyennes le long de la direction $x$, $(\langle y(t)\rangle ,\langle p_{y}(t)\rangle )$. La figure 2 montre les centroïdes des diagrammes de dispersion de l'espace de phase pour chaque sujet avec une ellipse représentant l'intervalle de confiance à un écart-type. Notez que les valeurs ne sont rapportées que pour les stimuli intacts car une analyse de la variance montre que les films brouillés et intacts ne se distinguent pas dans l'espace des phases ($P<0.85$, Tukey ajusté).

Les figures 2A et B montrent la projection du centroïde de l'espace des phases sur le plan enjambé par $x$ et $p_{x}$ pour "Bang ! You're Dead » et « Taken » respectivement, et le plan Fig. 2C et D ($y,p_{y}$). La position moyenne le long de l'axe $y$, $(\langle y\rangle )$ pour le stimulus intact (« BYD » et « Prise ») et leurs formes brouillées sont significativement différentes des homologues de repos pré-stimulus avec $P<0.001$ (ajustement de Tukey) alors que les centroïdes positifs à la tâche et au repos sont indiscernable dans le plan $x$ ( $P<0.05$, Tukey ajusté).

Les moyennes du groupe sont rapportées dans le tableau 11 avec leurs écarts-types. Ces valeurs sont la valeur moyenne des centroïdes (moyenne des points centraux des stimuli sur la figure 2) pour la position/le moment respectif dans chaque niveau de stimulus. Comme on le voit également sur les figures 2C et D, il existe une différence frappante d'un ordre de grandeur pour $\langle y\rangle$ entre les conditions de repos et de tâche, mais aucune différence marquée $x$, $\langle p_{x}\rangle$dans $\langle p_{y}\rangle$.

Figure 2 : Centroïdes moyens de l'espace de phase pour chaque sujet. Les ellipses représentent l'intervalle de confiance à 1 écart type. Les centroïdes des stimuli brouillés ont été omis car ils ne peuvent pas être distingués des stimuli intacts (P > 0,85) (A) Centroïdes pour "Bang ! Tu es mort » le long de la direction x. (B) Centroïdes pour "Prise" le long de la direction x. (C) Centroïdes pour "Bang ! Tu es mort » dans la direction y. (D) Centroïdes pour "Prise" le long de la direction y. Les différences ne sont apparentes que dans la direction y (P < 0,001, ajusté de Tukey) indiquant le niveau plus élevé d'activation antérieure comme indiqué sur la Fig. 1.

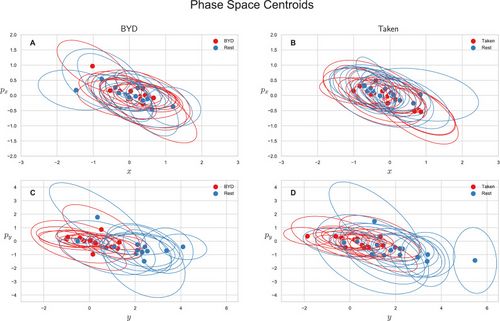
Tableau 1

Moyennes de groupe des centroïdes.

Stimulus	$\langle x\rangle$	$\langle y\rangle$	$\langle p_{x}\rangle$	$\langle p_{y}\rangle$
Pris	$(-1.4\pm 5.8)\times 10^{-1}$	$(2.4\pm 8.0)\times 10^{-1}$	$(-5.8\pm 27.0)\times 10^{-2}$	$(-1.0\pm 4.1)\times 10^{-1}$
Prise brouillée	$(-7.7\pm 35.0)\times 10^{-2}$	$(1.1\pm 9.3)\times 10^{-1}$	$(4.1\pm 13.0)\times 10^{-2}$	$(6.3\pm 35.0)\times 10^{-2}$
Claquer! Tu es mort	$(1.2\pm 4.7)\times 10^{-1}$	$(3.5\pm 74.0)\times 10^{-2}$	$(2.6\pm 33.0)\times 10^{-2}$	$(-3.0\pm 42.0)\times 10^{-1}$
Claquer! Vous êtes mort brouillé	$(1.4\pm 5.7)\times 10^{-1}$	$(-2.6\pm 7.5)\times 10^{-1}$	$(-1.5\pm 2.8)\times 10^{-1}$	$(-5.5\pm 53.0)\times 10^{-2}$
Repos (pré-pris)	$(-1.3\pm 4.6.0)\times 10^{-1}$	$(2.0\pm 1.4)\times 10^{0}$	$(9.1\pm 19.0)\times 10^{-2}$	$(-6.3\pm 7.3)\times 10^{-1}$
Repos (pré-BYD)	$(1.1\pm 66.0)\times 10^{-3}$	$(1.9\pm 1.2)\times 10^{0}$	$(1.0\pm 26.0)\times 10^{-2}$	$(-4.3\pm 7.5)\times 10^{-1}$

Des différences significatives ne sont notées que pour le reste acquis avant Taken et Bang ! Vous êtes mort lorsque vous comparez l'emplacement y moyen à l'un de leurs homologues de tâche (stimulus brouillés et intacts).

Moyennes de groupe des centroïdes.

Cette analyse a révélé deux résultats notables. Premièrement, il y avait un manque de différences significatives dans les impulsions du cerveau le long de la direction x et y. Deuxièmement, les moyennes des impulsions n'étaient pas significativement différentes de 0 au niveau du groupe. Les impulsions positives ou négatives proviennent de la dérivée temporelle concurrente de la probabilité et de l'emplacement de l'électrode. Puisque la moyenne des moments est de 0, il y a un nombre égal d'électrodes antérieures et postérieures avec à la fois des augmentations et des diminutions de probabilité.

De plus, nous avons examiné les changements dans les valeurs de probabilité dans les états de repos et d'activité. Des animations des distributions de probabilité sont présentes dans le matériel supplémentaire 1. Dans ces animations, les différences de repos et de tâche sont apparentes à travers l'évolution de la probabilité dans le temps.

Principe incertain.

Malgré la confirmation des résultats neuroscientifiques antérieurs et le succès apparent de notre modèle quasi-quantique, notre question de recherche telle que posée ci-dessus ne reste qu'à moitié résolue. En utilisant ce modèle, nous avons noté des différences dans les distributions de probabilité et les centroïdes de l'espace des phases au repos par rapport à la tâche. Cependant, nous cherchions toujours un paramètre du modèle qui resterait le même en repos et en tâche. À cette fin, nous avons défini un principe d'incertitude de Heisenberg analogue de la forme,

$\bigtriangleup x(t)\bigtriangleup p_{x}(t)\geq K_{brain}$

$(5)$

Le tableau 2 affiche les valeurs de cette constante ($K_{brain}$) acquises dans toutes les conditions, ainsi que la valeur maximale, la valeur moyenne et l'écart type. Nous avons constaté que ce modèle quasi-quantique conduit à une valeur minimale constante entre $\Delta x(t)\Delta p_{x}(t)$ et $\Delta y(t)\Delta p_{y}(t)$ de $0,78\pm 0,41{\tfrac {cm^{2}}{4ms}}$ avec $T=0,P=1$.

Notez que l'unité de ${\tfrac {cm^{2}}{4ms}}$ est le résultat de l'EEG échantillonné à 250 Hz et que la masse est considérée comme l'unité. De plus, la valeur moyenne et l'écart type de ces quantités restent cohérents dans toutes les conditions avec une valeur moyenne de $9,3\pm 4,4{\tfrac {cm^{2}}{4ms}}$( $T=0,P=1$) et un écart type de $18\pm 29{\tfrac {cm^{2}}{4ms}}$($T=0,P=1$).

Notamment, la valeur maximale varie entre les conditions, la valeur la plus élevée se produisant lorsque les sujets regardaient le clip intact de Bang ! Tu es mort. Bien que la position moyenne du signal le long de la direction y soit différente au repos que pendant une tâche ($P<0.001$), la méthodologie mathématique quasi-quantique conduit à une valeur d'incertitude constante.

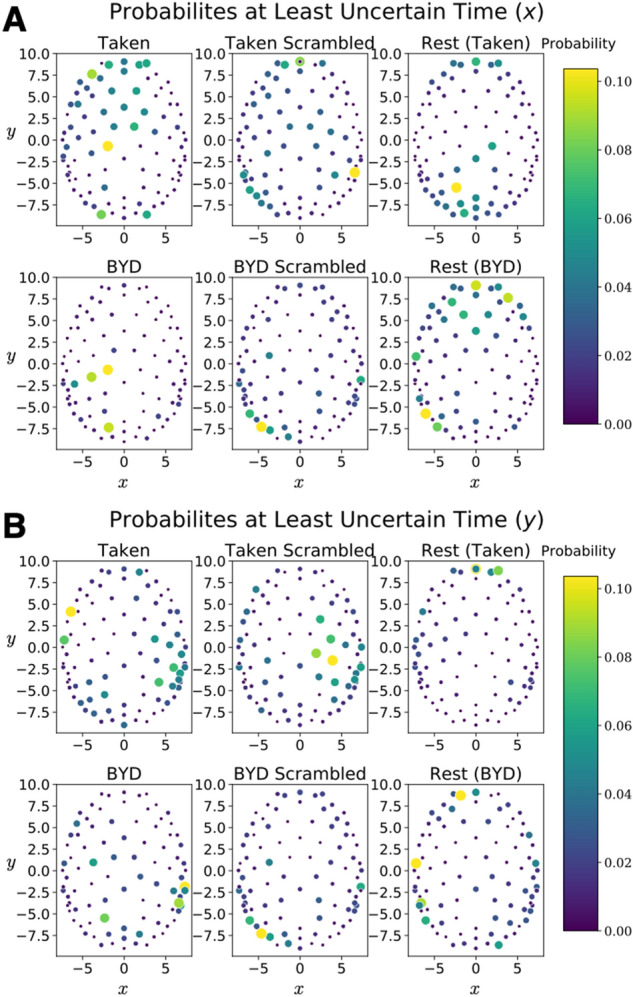
De manière assez remarquable, les valeurs du tableau montrent que l'incertitude moyenne et l'incertitude minimale sont les mêmes dans différentes conditions, malgré des maxima variant de plus de deux ordres de grandeur. Ainsi, donner plus de crédibilité à l'idée que cette relation d'incertitude capture les similitudes du cerveau dans des conditions très différentes. La figure 3 affiche la distribution de probabilité au moment correspondant au minimum d'incertitude pour $x$ et $y$.

Table 2

Différentes valeurs extraites des évolutions temporelles des produits $\Delta x(t)\Delta p_{x}(t)$ and $\Delta y(t)\Delta p_{y}(t)$.

Stimulus	$\Delta x\Delta p_{x}$	$\Delta y\Delta p_{y}$	$\Delta x\Delta p_{x}$	$\Delta y\Delta p_{y}$	$\Delta x\Delta p_{x}$	$\Delta y\Delta p_{y}$	$\Delta x\Delta p_{x}$	$\Delta y\Delta p_{y}$
Pris	${\textstyle (7\pm 2.1)10^{-1}}$	${\textstyle (7.2\pm 1.8)10^{-1}}$	${\textstyle (1.9\pm 1.0)10^{3}}$	${\textstyle (1.4\pm 0.8)10^{3}}$	${\textstyle (8.2\pm 2.2)10^{0}}$	${\textstyle (8.2\pm 2.2)10^{0}}$	${\textstyle (1.4\pm 0.4)10^{1}}$	${\textstyle (1.3\pm 0.4)10^{1}}$
Prise brouillée	${\textstyle (6.4\pm 2.6)10^{-1}}$	${\textstyle (6.8\pm 2.1)10^{-1}}$	${\textstyle (1.7\pm 1.2)10^{3}}$	${\textstyle (2.1\pm 2.2)10^{3}}$	${\textstyle (8.1\pm 1.9)10^{0}}$	${\textstyle (7.8\pm 2.0)10^{0}}$	${\textstyle (1.4\pm 0.4)10^{1}}$	${\textstyle (1.4\pm 0.7)10^{1}}$
Claquer! Tu es mort	${\textstyle (7.6\pm 4.9)10^{-1}}$	${\textstyle (7.5\pm 3.1)10^{-1}}$	${\textstyle (0.1\pm 3.1)10^{5}}$	${\textstyle (0.7\pm 1.4)10^{4}}$	${\textstyle (9.4\pm 6.7)10^{0}}$	${\textstyle (8.3\pm 3.6)10^{0}}$	${\textstyle (4.1\pm 8.9)10^{1}}$	${\textstyle (2.7\pm 3.9)10^{1}}$
Claquer! Vous êtes mort brouillé	${\textstyle (7.4\pm 3.2)10^{-1}}$	${\textstyle (7.1\pm 2.9)10^{-1}}$	${\textstyle (2.5\pm 1.2)10^{3}}$	${\textstyle (2.5\pm 1.6)10^{3}}$	${\textstyle (9.3\pm 5.1)10^{0}}$	${\textstyle (8.6\pm 4.4)10^{0}}$	${\textstyle (1.6\pm 0.7)10^{1}}$	${\textstyle (1.5\pm 0.8)10^{1}}$
Repos (pré-pris)	${\textstyle (9.7\pm 4.2)10^{-1}}$	${\textstyle (1.1\pm 0.6)10^{0}}$	${\textstyle (3.5\pm 3.1)10^{2}}$	${\textstyle (3.5\pm 1.7)10^{2}}$	${\textstyle (9.6\pm 2.1)10^{0}}$	${\textstyle (1.3\pm 0.4)10^{1}}$	${\textstyle (1.5\pm 0.8)10^{1}}$	${\textstyle (1.9\pm 0.7)10^{1}}$
Repos (pré-BYD)	${\textstyle (6.3\pm 3.7)10^{-1}}$	${\textstyle (8.6\pm 6.1)10^{-1}}$	${\textstyle (3.7\pm 2.0)10^{2}}$	${\textstyle (4.3\pm 2.5)10^{2}}$	${\textstyle (8.7\pm 3.3)10^{0}}$	${\textstyle (1.2\pm 0.6)10^{1}}$	${\textstyle (1.4\pm 0.5)10^{1}}$	${\textstyle (1.9\pm 0.8)10^{1}}$

Considérant la valeur minimale que ces produits atteignent pour chaque sujet, nous voyons une valeur constante en x et y de $0,78\pm 0,41{\tfrac {cm^{2}}{4ms}}$, une valeur moyenne de $9,3\pm 4,4{\tfrac {cm^{2}}{4ms}}$ et un écart type constant de $18\pm 29{\tfrac {cm^{2}}{4ms}}$. L'unité de ${\tfrac {cm^{2}}{4ms}}$ provient de l'échantillonnage de 250 Hz. Les valeurs maximales diffèrent selon la stimulation. Les valeurs sont rapportées sous forme de moyenne entre les sujets plus ou moins 1 écart type.

Figure 3: Cartes de probabilité correspondant au point temporel le moins incertain pour chacune des six conditions expérimentales. (A) Les probabilités qui conduisent à l'incertitude minimale telle que définie par le minimum de $\Delta x(t)\Delta p_{x}(t)$. (B) Les probabilités qui conduisent à l'incertitude minimale telle que définie par le minimum de $\Delta y(t)\Delta p_{y}(t)$ . Un sujet est affiché pour tous les stimuli pris, et un autre pour tous les stimuli Bang ! Vous êtes des stimuli morts.

Discussion

Dans la présente étude, nous avons étudié l'étendue spatiale et les propriétés transitoires associées de l'activité neuronale dans le cerveau pendant les conditions actives et de repos, et si des propriétés de réseau sous-jacentes similaires existent. Nous avons constaté que l'application de la transformation de Hilbert aux données EEG et sa normalisation (Eq. 2) impose une structure probabiliste au signal EEG à travers le cerveau (Eq. 3), que nous avons utilisée pour identifier la probabilité des modèles spatiaux d'activité ainsi que les transitions en activité sur tout le cuir chevelu. Nous avons trouvé plus d'activité antérieure pendant le repos par rapport à l'observation du film, à la fois dans l'amplitude et dans l'espace de phase. Cette constatation est conforme aux résultats précédents montrant une activation accrue dans la région antérieure pendant le repos. De plus, en normalisant les signaux EEG transformés de Hilbert et en extrayant des valeurs moyennes similaires à celles de la formulation de la fonction d'onde de la mécanique quantique, nous avons pu calculer l'incertitude de la «position» et de la «momentum» pendant le repos et le visionnage de films, qui est définie par la nouvelle constante $K_{brain}=0,78\pm 0,41{\tfrac {cm^{2}}{4ms}}$

Il est séduisant d'associer la constante liée à la «position» et à la «momentum» de l'activité neuronale à un principe fondamental, tel que le principe d'incertitude de Heisenberg. Cependant, on ne sait toujours pas ce que signifie cette incertitude. Cela pourrait impliquer des limites au degré auquel le cerveau est accessible ; l'augmentation des informations sur l'emplacement précis de l'état du cerveau (tel que décrit par nos «fonctions d'onde» quasi-quantiques) produira une plus grande incertitude quant à l'endroit où il se trouvera à un moment ultérieur. Ces résultats offrent une perspective intéressante sur le lien entre la fonction neuronale et les processus cognitifs. Par exemple, à mesure que la "fonction d'onde" se localise dans l'espace le long d'un train de pensées, nous devenons distraits pour augmenter l'incertitude, ce qui peut expliquer pourquoi les esprits errent et les pensées sont éphémères ?

La valeur $K_{b}$ que nous avons trouvée est-elle constante dans différentes conditions de stimulation et indépendante du nombre d'électrodes utilisées pour acquérir les données ? Pour tester cela, nous avons échantillonné les électrodes EEG de 92 à 20 et effectué la même analyse que dans le texte principal. Conformément aux 92 canaux, nous avons trouvé la tendance antérieure au repos, mais nous avons constaté que la réduction des électrodes à 20 entraînait une constante différente $K_{b}=0,03\pm 0,02{\tfrac {cm^{2}}{4ms}}$ (voir le matériel supplémentaire).

Cela démontre que le modèle est capable de capturer les différences de repos/tâche, mais une condition de normalisation dépendante du montage peut devoir être introduite.

Il est important de noter que les valeurs d'incertitude de cette forme sont inhérentes à toute variable conjuguée de Fourier, car une valeur s'étale dans une variable, elle se localise dans l'autre. Cela suggère qu'après avoir défini le carré de l'évolution temporelle de l'électrode EEG transformée de Hilbert comme étant la probabilité et imposé les propriétés d'un espace de Hilbert sur les signaux d'électrode, une valeur d'incertitude peut être extraite. En mécanique quantique, cette incertitude fixe la limite des échelles non observables. Cette approche a été inspirée par le besoin en neurosciences de nouveaux modèles pour aider à interpréter les données de neuroimagerie. Bien qu'il s'agisse d'une avancée méthodologique intéressante, nous devons encore déterminer si l'incertitude observée dans les données EEG est soutenue par un nouveau principe fondamental comme en mécanique quantique, ou si c'est simplement le résultat d'avoir construit deux nouvelles variables conjuguées de Fourier à partir du Signal EEG.

Des travaux supplémentaires doivent être effectués pour explorer cette constante en ce qui concerne la riche taxonomie des tâches et des stimuli et les différents états de conscience qui sont couramment utilisés en neurosciences cognitives. Cette méthodologie pourrait être étendue à l'IRMf, où les cours temporels BOLD pourraient être transformés par Hilbert, créant ainsi un analogue tridimensionnel du modèle EEG présenté dans cet article.

En fin de compte, cet article a présenté une nouvelle méthodologie pour analyser les données EEG. Normaliser les données et les traiter comme une amplitude de probabilité a conduit à des paramètres qui changeaient avec la présence ou l'absence de stimulus, tout en établissant simultanément une valeur constante indépendante du stimulus. Nous avons appliqué avec succès un cadre mathématique basé sur les formalismes de la mécanique quantique au paradigme du repos et de la tâche en EEG (sans prétendre que le cerveau est un objet quantique). Alors que les neurosciences continuent d'évoluer, les outils analytiques à leur disposition doivent également progresser en conséquence. Nous espérons que cet outil analytique, ainsi que les progrès de la modélisation et de l'apprentissage automatique, nous aideront à comprendre la nature de la conscience.

Méthodes

L'acquisition des données

Vingt-huit sujets sains ont été recrutés au Brain and Mind Institute de l'Université de Western Ontario, au Canada, pour participer à cette étude. Un consentement écrit éclairé a été obtenu avant le test de tous les participants. L'approbation éthique de cette étude a été accordée par le comité d'éthique de la recherche en sciences de la santé et le comité d'éthique de la recherche non médicale de l'Université de Western Ontario et toutes les recherches ont été effectuées conformément aux lignes directrices/règlements pertinents et conformément à la Déclaration d'Helsinki.

Deux extraits de films pleins de suspense ont été utilisés comme stimuli naturalistes dans cette étude. Un extrait vidéo du film muet « Bang ! You're Dead" et un extrait audio du film "Taken" ont été montrés à 13 et 15 sujets respectivement dans leurs formes originales intactes et brouillées. Avant les deux acquisitions, une section de repos a été acquise où les sujets ont été invités à se détendre, sans aucune stimulation manifeste. La présentation du stimulus a été contrôlée avec le plugin Psychtoolbox pour MATLAB sur un Apple MacBook Pro 15″. L'audio a été présenté de manière binaurale à un volume d'écoute confortable via les écouteurs Etymotics ER-1.

Les données EEG ont été recueillies à l'aide d'un capuchon à 129 canaux (Electrical Geodesics Inc. [EGI], Oregon, États-Unis). Les impédances des électrodes ont été maintenues en dessous de 50 kΩ avec des signaux échantillonnés à 250 Hz et référencés au sommet central (Cz). À l'aide de la boîte à outils EEGLAB MATLAB, les canaux bruyants ont été identifiés et supprimés, puis réinterpolés dans les données. Un test de Kolmogorov-Smirnov (KS) sur les données a été utilisé pour identifier les régions qui n'étaient pas gaussiennes. L'analyse des composants indépendants (ICA) a ensuite été utilisée pour identifier visuellement les modèles d'activité neuronale caractéristiques des mouvements oculaires et musculaires qui ont ensuite été supprimés des données. Le prétraitement EEG a été effectué individuellement pour chaque sujet et condition.

Parmi les deux extraits de films testés, le premier était un segment de 8 minutes du film muet télévisé d'Alfred Hitchcock "Bang ! Tu es mort". Cette scène met en scène un garçon de 5 ans qui ramasse le revolver de son oncle. Le garçon charge une balle dans le pistolet et joue avec comme s'il s'agissait d'un jouet. Le garçon (et le spectateur) sait rarement si l'arme a une balle dans sa chambre et le suspense monte lorsque le garçon fait tourner la chambre, la pointe vers les autres et appuie sur la gâchette. Comme alternative à la stimulation visuelle, un extrait audio de 5 minutes du film "Taken" a également été utilisé. Ce clip dépeint une conversation téléphonique dans laquelle un père surprend l'enlèvement de ses filles.

De plus, deux stimuli de contrôle « brouillés » ont été utilisés, un pour chaque film. Cela sépare les réponses neuronales suscitées par les propriétés sensorielles de regarder ou d'écouter les films de celles impliquées dans le suivi de l'intrigue. La version brouillée de "Bang ! You're Dead » a été généré en isolant les segments de 1 s et en mélangeant les segments de manière pseudo-aléatoire, éliminant ainsi la cohérence temporelle du récit. La version brouillée de "Taken" a été créée en faisant tourner spectralement l'audio, rendant ainsi le discours indéchiffrable. Les extraits de films brouillés ont été présentés avant les versions intactes pour éviter les effets de report potentiels du récit. Avant que les sujets regardent/écoutent le stimulus brouillé, un court segment d'EEG au repos a été acquis.

Modèle

Chacune des j électrodes est décrite par un couple ordonné ($x_{j},y_{j},z_{j}$) dans un espace tridimensionnel. Pour compléter cette analyse, les électrodes ont d'abord été projetées sur le plan ($x,y$) en supprimant la profondeur de la tête. La figure 1A montre les emplacements de chaque électrode dans cet espace 2d. Suite à cette projection, les cours du temps pour chacune des 92 électrodes ont été transformés de Hilbert puis normalisés en suivant la procédure indiquée à l'aide de l'Eq. (2). Une probabilité a été définie dans cet espace de position d'électrode comme le carré de l'évolution temporelle de la transformée de Hilbert (Eq. 3), analogue aux fonctions d'onde de la mécanique quantique. Huit régions Antérieure G/D, Postérieure G/D, Pariétale G/D, Occipitale G/D) ont ensuite été définies en regroupant les 92 électrodes, et les fréquences d'entrée dans chaque région fG ont été obtenues en sommant les probabilités des électrodes au sein du groupe, puis intégration dans le temps.

$Prob_{G}(t)=\sum _{j=1}^{92}\Psi _{k}^{*}(t)\times \Psi _{k}(t);f_{G}={\tfrac {1}{T}}\sum _{j=1}^{T}Prob_{G}(t)$

$(6)$

où chacun des huit groupes désignés par l'indice a un nombre différent d'électrodes constitutives N. Dans l'occipital gauche et droit il y a 10 électrodes chacun, dans le pariétal gauche et droit il y a 17 électrodes chacun, dans la partie postérieure gauche et droite il y a sont respectivement 10 et 11 électrodes, et dans les parties antérieures gauche et droite, il y a respectivement 8 et 9 électrodes.

Après avoir obtenu les fréquences de niveau de groupe, les valeurs moyennes pour la position et l'élan ont été calculées à l'aide des équations. (4) et (5) (avec des expressions identiques pour y). Enfin, pour vérifier notre principe d'incertitude analogue, nous avons cherché des expressions de la forme

$\bigtriangleup x={\sqrt {\langle x^{2}(t)\rangle -\langle x(t)\rangle ^{2}}};\bigtriangleup p_{x}={\sqrt {\langle p_{x}^{2}(t)\rangle -\langle p_{x}(t)\rangle ^{2}}}$

$(7)$

L'expression pour peut être facilement appliquée aux probabilités et positions telles que définies ci-dessus, résultant en le premier terme donné par

$\langle x^{2}(t)\rangle =\sum _{j=1}^{92}P_{j}(t)x_{j}^{2}$

$(8)$

Et le second terme donné par le carré de l'Eq. (4). Le second terme de $\Delta P_{x}$ est donné par le carré de l'Eq. (5), mais le premier terme est plus nuancé. Cela est dû au nombre complexe renvoyé en agissant deux fois sur l'opérateur dérivé sur la probabilité. Pour surmonter cela, des transformées de Fourier ont été utilisées pour modifier l'équation. (5) dans la base de quantité de mouvement qui a ensuite permis le calcul efficace de $P_{x}^{2}(t)$.

En désignant ${\tilde {P}}_{j}(t)$ comme la probabilité impulsion-espace obtenue par une transformée de Fourier bidimensionnelle non uniforme de la pseudo-fonction d'onde de l'espace de position, Eq. (5) peut être réécrit comme,

$\langle p_{x}(t)\rangle =\sum _{j=1}^{92}{\tilde {P}}_{j}(t)p_{j}$

$(9)$

Conduisant au premier terme de l'expression à écrire comme,

$\langle p_{x}^{2}(t)\rangle =m^{2}\sum _{j=1}^{92}{\tfrac {x_{j}^{2}}{{\tilde {p}}_{j}(t)}}[{d \over dt}P_{j}(t)]^{2}$

$(10)$

Le wrapper python FINUFFT a été utilisé pour prendre la transformée de Fourier en utilisant une FFT non uniforme de type 3, 2d, et la valeur minimale dans le temps de la relation d'incertitude a été trouvée. Des points dans l'espace d'impulsion ont été échantillonnés sur $p_{x}\in [-4,4]$ et $p_{y}\in [-4,5]$ avec les deux points supplémentaires ($[-5,-4]$) et ($[-4,-5]$). La figure 4 montre les probabilités de position et d'impulsion respectivement dans leur propre base. Matériel supplémentaire 2.

Figure 4: (A) Distribution de probabilité pour un seul sujet dans la base de position. (B) Distribution de probabilité de base de l'élan pour un seul sujet. Les valeurs de quantité de mouvement utilisées pour la transformée de Fourier sont indiquées par les emplacements des points. Les points sont codés par couleur/taille pour représenter la valeur de probabilité à cet emplacement.

Pour calculer les valeurs rapportées dans le tableau 2, la valeur correspondante a été trouvée pour chaque sujet, et celles-ci ont été utilisées pour calculer la moyenne du groupe rapportée ici.

Information supplémentaire

Figures supplémentaires.(28M, docx)

Informations supplémentaires.(375K, docx)

Remerciements

Nous tenons à remercier Silvano Petrarca pour son aide continue dans la conception du modèle. Cette étude a été financée par la Subvention à la découverte du CRSNG (05578-2014RGPIN), CERC (215063), Fonds de la Fondation des CIHR (167264). AMO est Fellow du programme Cerveau, esprit et conscience de l'CIFAR.

Contributions d'auteur

N.J.M.P., C.M. et G.L. ont effectué l'analyse. A.S., B.S. et N.J.M.P. développé le modèle. COMME. et BS supervisé l'analyse. N.J.M.P., A.S., G.L. et B.S. écrit le manuscrit. A.M.O. révisé le manuscrit.

Intérêts concurrents

Les auteurs ne déclarent aucun intérêt concurrent.

Notes de bas de page

Note de l'éditeur

Springer Nature reste neutre en ce qui concerne les revendications juridictionnelles dans les cartes publiées et les affiliations institutionnelles.

Ces auteurs ont contribué à parts égales : Bobby Stojanoski et Andrea Soddu.

Information supplémentaire

La version en ligne contient du matériel supplémentaire disponible au 10.1038/s41598-021-97960-7.

Informations sur l'article

Sci Rep. 2021; 11: 19771.

Published online 2021 Oct 5. doi: 10.1038/s41598-021-97960-7

PMCID: PMC8492705

PMID: 34611185

Nicholas J. M. Popiel,^1,2 Colin Metrow,¹ Geoffrey Laforge,³ Adrian M. Owen,^3,4,5 Bobby Stojanoski,^#4,6 and Andrea Soddu^#1,3

¹The Department of Physics and Astronomy, The University of Western Ontario, London, ON N6A 5B7 Canada

²Cavendish Laboratory, University of Cambridge, Cambridge, CB3 0HE UK

³The Brain and Mind Institute, The University of Western Ontario, London, ON N6A 5B7 Canada

⁴The Department of Psychology, The University of Western Ontario, London, ON N6A 5B7 Canada

⁵The Department of Physiology and Pharmacology, The University of Western Ontario, London, ON N6A 5B7 Canada

⁶Faculty of Social Science and Humanities, University of Ontario Institute of Technology, 2000 Simcoe Street North, Oshawa, ON L1H 7K4 Canada

Andrea Soddu, Email: asoddu@uwo.ca

Corresponding author.

1. Contributed equally.

Received 2021 Apr 28; Accepted 2021 Aug 30.

Copyright © The Author(s) 2021

Libre accès

Cet article est sous licence Creative Commons Attribution 4.0 International, qui autorise l'utilisation, le partage, l'adaptation, la distribution et la reproduction sur tout support ou format, tant que vous donnez le crédit approprié à l'auteur ou aux auteurs originaux et à la source, fournissez un lien vers la licence Creative Commons, et indiquez si des modifications ont été apportées. Les images ou tout autre matériel de tiers dans cet article sont inclus dans la licence Creative Commons de l'article, sauf indication contraire dans une ligne de crédit au matériel. Si le matériel n'est pas inclus dans la licence Creative Commons de l'article et que votre utilisation prévue n'est pas autorisée par la réglementation légale ou dépasse l'utilisation autorisée, vous devrez obtenir l'autorisation directement du détenteur des droits d'auteur. Pour voir une copie de cette licence, visitez http://creativecommons.org/licenses/by/4.0/.

Les articles des rapports scientifiques sont fournis ici avec l'aimable autorisation de == Nature Publishing Group ==

Bibliography & references

Masticationpedia is a charity, a not-for-profit organization operating in dentistry medical research,
particularly focusing on the field of the neurophysiology of the masticatory system
 

Home

Introduction

Latest chapter

Ed. Lab

Donate

Contacts