Logica di linguaggio fuzzy
| Other languages: |
In questo capitolo parleremo della logica fuzzy. Si chiama sfocato perché è caratterizzato da una gradualità: a un oggetto si può attribuire una qualità che può avere vari gradi di verità.
Nella prima parte di questo capitolo verrà discusso concettualmente il significato di verità graduata, mentre nella seconda parte approfondiremo il formalismo matematico introducendo la funzione di appartenenza : l'elemento che ci permette di sintetizzare matematicamente le sfumature di questa logica del linguaggio. È stato possibile dimostrare che con il ragionamento "fuzzy", a differenza delle precedenti logiche del linguaggio, le diagnosi mostrano meno incertezza. Nonostante ciò, però, si sente ancora la necessità di affinare ulteriormente il metodo linguistico e di arricchirlo di ulteriori “logiche”.
Introduzione
Siamo arrivati a questo punto perché, come colleghi, molto spesso ci troviamo di fronte a responsabilità e decisioni molto difficili da prendere e entrano in gioco questioni come la coscienza, l'intelligenza e l'umiltà. In una situazione del genere, però, ci troviamo di fronte a due ostacoli altrettanto difficili da gestire quello dello '' (Conoscenza Base), discusso nel capitolo 'Logica del linguaggio probabilistico',e che in questo contesto codifichiamo in (conoscenza di base limitata dal tempo ) ed un (conoscenza di base limitata dal contesto medico specialistico). Questi due parametri dell'epistemologia caratterizzano l'epoca scientifica in cui viviamo. Inoltre, sia lo che lo sono variabili dipendenti dalla nostra filogenesi, ed in particolar modo dalla nostra plasticità concettuale e attitudine al cambiamento.[1]
(Ti faccio un esempio pratico)
Quante ricerche sono state prodotte sul tema 'Logica fuzzy'?
Pubmed risponde con 2862 articoli negli ultimi 10 anni,[2][3] tanto da poter dire che il tema è attuale e sufficientemente aggiornato. Tuttavia, se volessimo concentrare l'attenzione su un argomento specifico come "Disturbi temporo-mandibolari", il database risponderà con ben 2.235 articoli.[4] Quindi, se volessimo controllare un altro argomento come "Dolore orofacciale", Pubmed ci fornisce 1.986 articoli.[5] Ciò significa che lo per questi tre argomenti negli ultimi 10 anni è stato sufficientemente aggiornato.
Se, ora, volessimo verificare l'interconnessione tra gli argomenti, noteremo che nei contesti sarà il seguente:
L'esempio significa che lo è relativamente aggiornato individualmente per i tre argomenti mentre diminuisce drasticamente quando gli argomenti tra i contesti vengono uniti e in particolare a 9 articoli per il punto 1 e persino a 0 articoli per il punto 2. Quindi, lo è una variabile dipendente dal tempo mentre lo è una variabile cognitiva dipendente dalla nostra attitudine al progresso della scienza, come già accennato – tra l'altro – nel capitolo 'Introduzione'.
(Aspetta e vedrai)
Abbiamo concluso il capitolo precedente affermando che la logica di un linguaggio classico e successivamente la logica probabilistica ci hanno aiutato molto nel progresso della scienza medica e della diagnostica ma portano implicitamente dentro di sé i limiti della propria logica del linguaggio, che limita la visione della l'universo biologico. Abbiamo anche verificato che con la logica di un linguaggio classico, per così dire Aristotelico, la sintassi logica che ne deriva nella diagnostica della nostra Mary Poppins limita, di fatto, la conclusione clinica.
Il predicato (vedi capitolo Logica di linguaggio classica),
sostiene che:
"ogni paziente normale che risulta positivo all'esame radiografico dell'ATM ha un TMDs , e che come diretta conseguenza essendo Mary Poppins positiva (ed è anche una paziente "normale") alla radiografia dell'ATM è anche è affetta da TMD .
La limitazione del percorso logico seguito ci ha portato ad intraprendere un percorso alternativo, in cui si evita la bivalenza o natura binaria della logica del linguaggio classico e si segue un modello probabilistico. Il collega dentista, infatti, ha cambiato vocabolario e ha preferito una conclusione del tipo:
e cioè che la nostra Mary Poppins è affetta per il 95% da TMD poiché ha una degenerazione dell'articolazione temporo-mandibolare supportata dalla positività del dato in un campione di popolazione . Tuttavia, abbiamo anche riscontrato che nel processo di costruzione probabilistica logica (Analysandum che ha permesso di formulare le suddette conclusioni diagnostiche differenziali e scegliere quella più plausibile, c'è un elemento cruciale all'intero dello Analysand rappresentato dal termine . Quest'ultimo indica, nello specifico, una 'Base di conoscenza' del contesto su cui si costruisce la logica del linguaggio probabilistico.
Abbiamo quindi concluso che forse il collega odontoiatra avrebbe dovuto venire a conoscenza della propria 'Incertezza Soggettiva' (affetta da TMD o nOP?) e 'Incertezza Oggettiva' (probabilmente più affetta da TMD o nOP?).
Perché siamo giunti a queste conclusioni critiche?
Per una forma ampiamente condivisa di rappresentazione della realtà, supportata dalla testimonianza di autorevoli figure che ne confermano la criticità. Ne è scaturita una visione della realtà che, a prima vista, sembrerebbe inadatta al linguaggio medico. Le espressioni, infatti, come “circa 2” o “moderatamente” possono suscitare legittime perplessità e sembrare un anacronistico ritorno a concetti prescientifici. Al contrario, però, l'uso di numeri fuzzy o asserzioni consente di trattare dati scientifici in contesti in cui non si può parlare di "probabilità" ma solo di "possibilità"..[8]
Fuzzy truth
In the ambitious attempt to mathematically translate human rationality, it was thought in the mid-twentieth century to expand the concept of classical logic by formulating fuzzy logic. Fuzzy logic concerns the properties that we could call ‘graduality’, i.e., which can be attributed to an object with different degrees. Examples are the properties ‘being sick’, ‘having pain’, ‘being tall’, ‘being young’, and so on.
Mathematically, fuzzy logic allows us to attribute to each proposition a degree of truth between and . The most classic example to explain this concept is that of age: we can say that a new-born has a ‘degree of youth’ equal to , an eighteen-year-old equal to , a sixty-year-old equal to , and so on
In the context of classical logic, on the other hand, the statements:
- a ten-year-old is young
- a thirty-year-old is young
are both true. However, in the case of classical logic (which allows only the two true or false data), this would mean that the infant and the thirty-year-old are equally young. Which is obviously wrong.
The importance and the charm of fuzzy logic arise from the fact that it is able to translate the uncertainty inherent in some data of human language into mathematical formalism, coding ‘elastic’ concepts (such as almost high, fairly good, etc.), in order to make them understandable and manageable by computers.
Set theory
As mentioned in the previous chapter, the basic concept of fuzzy logic is that of multivalence, i.e., in terms of set theory, of the possibility that an object can belong to a set even partially and, therefore, also to several sets with different degrees. Let us recall from the beginning the basic elements of the theory of ordinary sets. As will be seen, in them appear the formal expressions of the principles of Aristotelian logic, recalled in the previous chapter.
Quantifiers
- Membership: represented by the symbol (belongs), - for example the number 13 belongs to the set of odd numbers
- Non-membership: represented by the symbol (It does not belong)
- Inclusion: Represented by the symbol (is content), - for example the whole it is contained within the larger set , (in this case it is said that is a subset of )
- Universal quantifier, which is indicated by the symbol (for each)
- Demonstration, which is indicated by the symbol (such that)
Set operators
Given the whole universe we indicate with its generic element so that ; then, we consider two subsets and internal to so that and
The theory of fuzzy language logic is an extension of the classical theory of sets in which, however, the principles of non-contradiction and the excluded third are not valid. Remember that in classical logic, given the set and its complementary , the principle of non-contradiction states that if an element belongs to the whole it cannot at the same time also belong to its complementary ; according to the principle of the excluded third, however, the union of a whole and its complementary constitutes the complete universe .
In other words, if any element does not belong to the whole, it must necessarily belong to its complementary.
Fuzzy set and membership function
We choose - as a formalism - to represent a fuzzy set with the 'tilde':. A fuzzy set is a set where the elements have a 'degree' of belonging (consistent with fuzzy logic): some can be included in the set at 100%, others in lower percentages.
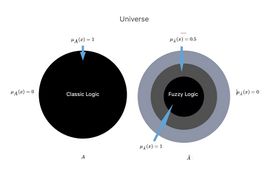
To mathematically represent this degree of belonging is the function called 'Membership Function'. The function is a continuous function defined in the interval where it is:
- if is totally contained in (these points are called 'nucleus', they indicate plausible predicate values).
- if is not contained in
- if is partially contained in (these points are called 'support', they indicate the possible predicate values).
The graphical representation of the function can be varied; from those with linear lines (triangular, trapezoidal) to those in the shape of bells or 'S' (sigmoidal) as depicted in Figure 1, which contains the whole graphic concept of the function of belonging.[9][10]
The support set of a fuzzy set is defined as the zone in which the degree of membership results ; on the other hand, the core is defined as the area in which the degree of belonging assumes value
The 'Support set' represents the values of the predicate deemed possible, while the 'core' represents those deemed more plausible.
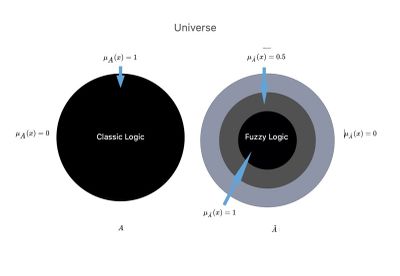
If represented a set in the ordinary sense of the term or classical language logic previously described, its membership function could assume only the values or , depending on whether the element belongs to the whole or not, as considered. Figure 2 shows a graphic representation of the crisp (rigidly defined) or fuzzy concept of membership, which clearly recalls Smuts's considerations.[11]
Let us go back to the specific case of our Mary Poppins, in which we see a discrepancy between the assertions of the dentist and the neurologist and we look for a comparison between classical logic and fuzzy logic:
Figure 2: Let us imagine the Science Universe in which there are two parallel worlds or contexts, and .
In the scientific context, the so-called ‘crisp’, and we have converted into the logic of Classic Language, in which the physician has an absolute scientific background information with a clear dividing line that we have named .
In another scientific context called ‘fuzzy logic’, and in which there is a union between the subset in that we can go so far as to say: union between .
We will remarkably notice the following deductions:
- Classical Logic in the Dental Context in which only a logical process that gives as results will be possible, or being the range of data reduced to basic knowledge in the set . This means that outside the dental world there is a void and that term of set theory is written precisely and which is synonymous with a high range of:
- Fuzzy logic in a dental context in which they are represented beyond the basic knowledge of the dental context also those partially acquired from the neurophysiological world will have the prerogative to return a result and a result because of basic knowledge which at this point is represented by the union of dental and neurological contexts. The result of this scientific-clinical implementation of dentistry would allow a «Reduction of differential diagnostic error»
Consideraciones finales
Los temas que podían distraer la atención del lector eran, de hecho, esenciales para demostrar el mensaje. Normalmente, en efecto, cuando cualquier mente más o menos brillante se permite arrojar una piedra al estanque de la Ciencia, se genera una onda expansiva, propia del período de la ciencia extraordinaria de Kuhn, contra la que se pelean la mayoría de los miembros de la comunidad científica internacional. De buena fe podemos decir que este fenómeno —en lo que se refiere a los temas que aquí abordamos— está bien representado en la premisa al inicio del capítulo.
En estos capítulos, en realidad, se ha abordado un tema fundamental para la ciencia: la reevaluación, el peso específico que siempre se le ha dado al , la toma de conciencia de los contextos científico/clínicos , habiendo emprendido un camino más elástico de la Lógica Difusa que el Clásica, dándose cuenta de la extrema importancia del y en definitiva de la unión de los contextos para aumentar su capacidad diagnóstica.[12][13]
En el próximo capítulo estaremos listos para emprender un camino igualmente fascinante: nos conducirá al contexto de una lógica de Lenguaje de Sistemas, y nos permitirá profundizar nuestro conocimiento, ya no solo en la semiótica clínica, sino en la comprensión de la lógica de sistemas. funciones (recientemente se está evaluando en disciplinas neuromotoras para la enfermedad de Parkinson).[14]
En Masticationpedia, por supuesto, informaremos sobre el tema 'Inferencia del sistema' en el campo del sistema masticatorio, como podemos leer en el próximo capítulo titulado 'Lógica del sistema'.
- ↑ Takeuchi S, Okuda S, «Knowledge base toward understanding actionable alterations and realizing precision oncology», in Int J Clin Oncol, 2019».
PMID:30542800 - PMCID:PMC6373253
DOI:10.1007/s10147-018-1378-0
This is an Open Access resource! - ↑ Fuzzy logic on Pubmed
- ↑ All statistics collected following visits to the Pubmed site (https://pubmed.ncbi.nlm.nih.gov/). Last checked: December 2020.
- ↑ Temporomandibular Disorders in Pubmed
- ↑ Orofacial Pain in Pubmed
- ↑ Temporomandibular disorders AND Orofacial Pain in Pubmed
- ↑ "Temporomandibular disorders AND Orofacial Pain AND Fuzzy logic" in Pubmed
- ↑ Dubois D, Prade H, «Fundamentals of Fuzzy Sets», Kluwer Academic Publishers, 2000, Boston».
- ↑ Zhang W, Yang J, Fang Y, Chen H, Mao Y, Kumar M, «Analytical fuzzy approach to biological data analysis», in Saudi J Biol Sci, 2017».
PMID:28386181 - PMCID:PMC5372457
DOI:10.1016/j.sjbs.2017.01.027 - ↑ Lazar P, Jayapathy R, Torrents-Barrena J, Mol B, Mohanalin, Puig D, «Fuzzy-entropy threshold based on a complex wavelet denoising technique to diagnose Alzheimer disease», in Healthc Technol Lett, The Institution of Engineering and Technology, 2016».
PMID:30800318 - PMCID:PMC6371778
DOI:10.1049/htl.2016.0022 - ↑ •SMUTS J.C. 1926, Holism and Evolution, London: Macmillan.
- ↑ Mehrdad Farzandipour, Ehsan Nabovati, Soheila Saeedi, Esmaeil Fakharian. Fuzzy decision support systems to diagnose musculoskeletal disorders: A systematic literature review . Comput Methods Programs Biomed. 2018 Sep;163:101-109. doi: 10.1016/j.cmpb.2018.06.002. Epub 2018 Jun 6.
- ↑ Long Huang, Shaohua Xu, Kun Liu, Ruiping Yang, Lu Wu. A Fuzzy Radial Basis Adaptive Inference Network and Its Application to Time-Varying Signal Classification . Comput Intell Neurosci, 2021 Jun 23;2021:5528291.
doi: 10.1155/2021/5528291.eCollection 2021. - ↑ Mehrbakhsh Nilashi, Othman Ibrahim, Ali Ahani. Accuracy Improvement for Predicting Parkinson's Disease Progression. Sci Rep. 2016 Sep 30;6:34181. doi: 10.1038/srep34181.
particularly focusing on the field of the neurophysiology of the masticatory system














































![{\displaystyle [0;1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc3bf59a5da5d8181083b228c8933efbda133483)