Difference between revisions of "Store:Asse Cerniera Verticale parte 2"
m (Gianni moved page Store:Asse Cerniera parte 2 to Store:Asse Cerniera Verticale parte 2) |
|||
| Line 342: | Line 342: | ||
Un fenomeno simile si osserva per il condilo mediotrusivo e gli incisivi, le cui traiettorie sono influenzate da traslazioni mediali e anteriori e da rotazioni attorno all’asse verticale. Questi tracciati non sono ellissi perfette, ma curve più complesse a causa delle variazioni nei movimenti condilari. | Un fenomeno simile si osserva per il condilo mediotrusivo e gli incisivi, le cui traiettorie sono influenzate da traslazioni mediali e anteriori e da rotazioni attorno all’asse verticale. Questi tracciati non sono ellissi perfette, ma curve più complesse a causa delle variazioni nei movimenti condilari. | ||
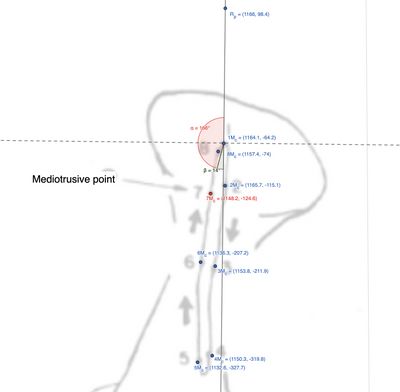
I tracciati dentali sono correlati ai movimenti dei condili e offrono preziose informazioni sulla cinematica mandibolare. Un modello basato su una conica passante per cinque punti strategici aiuta a rappresentare meglio queste traiettorie, come illustrato nella figura 10a. | I tracciati dentali sono correlati ai movimenti dei condili e offrono preziose informazioni sulla cinematica mandibolare, per cui sarebbe auspicabile spendere qualche parola in più sulla velocità del moto masticatorio e la rappresentazione di questa cinematica mandibolare in un forma geometrico/matematica chiamata 'Conica'. | ||
==Velocità lineare ed angolare== | |||
== Analisi del Movimento Simultaneo verso il Punto 1 == | |||
=== Fattori Considerati === | |||
**Sincronizzazione Temporale** | |||
Entrambi i condili devono completare il movimento di ritorno nello stesso intervallo di tempo (<math>t_{tot}</math>), indipendentemente dalla distanza percorsa. | |||
**Differenze nelle Distanze** | |||
- Condilo laterotrusivo (<math>L_c</math>): <math>d_{L_c} = 0.898 \, \text{mm}</math>. | |||
- Condilo mediotrusivo (<math>M_c</math>): <math>d_{M_c} = 2.61 \, \text{mm}</math>. | |||
**Velocità di Ritorno Necessaria** | |||
La velocità del <math>M_c</math> deve essere proporzionalmente maggiore per compensare la maggiore distanza percorsa nello stesso tempo. | |||
=== Calcolo della Velocità Necessaria === | |||
Assumiamo che il tempo di ritorno (<math>t_{tot}</math>) sia governato dal condilo <math>L_c</math>, la cui velocità media di ritorno è basata sul dato iniziale (<math>v_{L_c} = 224.5 \, \text{mm/s}</math>): | |||
<math>t_{tot} = \frac{d_{L_c}}{v_{L_c}} = \frac{0.898}{224.5} \approx 0.004 \, \text{s}</math> | |||
Per il condilo <math>M_c</math>, la velocità media necessaria (<math>v_{M_c}</math>) è: | |||
<math>v_{M_c} = \frac{d_{M_c}}{t_{tot}} = \frac{2.61}{0.004} \approx 652.5 \, \text{mm/s}</math> | |||
=== Interpretazione Biomeccanica === | |||
**Velocità Significativamente Maggiore nel <math>M_c</math>** | |||
Il condilo <math>M_c</math> deve operare con una velocità media di <math>652.5 \, \text{mm/s}</math>, quasi tripla rispetto a quella del <math>L_c</math> (<math>224.5 \, \text{mm/s}</math>). Questo incremento è necessario per sincronizzarsi con il condilo laterotrusivo, che percorre una distanza minore nello stesso intervallo di tempo. | |||
**Ruolo Funzionale del <math>M_c</math>** | |||
La velocità più alta del <math>M_c</math> riflette il suo ruolo dinamico e adattativo. Questo condilo deve compensare: | |||
- La maggiore distanza del tragitto. | |||
- La necessità di stabilizzare il movimento mandibolare e mantenere un equilibrio biomeccanico. | |||
**Efficienza del <math>L_c</math>** | |||
Il condilo <math>L_c</math>, percorrendo una distanza più breve, opera a velocità inferiori, indicando una maggiore stabilità durante i movimenti masticatori laterali. | |||
=== Conclusione === | |||
La maggiore distanza percorsa dal <math>M_c</math> richiede un incremento significativo della velocità di ritorno, raggiungendo <math>652.5 \, \text{mm/s}</math>, per sincronizzarsi con il condilo <math>L_c</math>. Questo fenomeno è un chiaro esempio di adattamento biomeccanico, dove la mandibola bilancia le differenze di distanza e velocità tra i due condili per garantire una chiusura armonica e simultanea. | |||
==Rappresentazione in una 'Conica'== | |||
Un modello basato su una conica passante per cinque punti strategici aiuta a rappresentare meglio queste traiettorie, come illustrato nella figura 10a. | |||
In sintesi, i tracciati dei molari e degli incisivi assumono forme ellittiche complesse, poiché il centro di rotazione condilare si sposta continuamente. Questo modello aiuta a comprendere meglio la complessità dei movimenti mandibolari. | In sintesi, i tracciati dei molari e degli incisivi assumono forme ellittiche complesse, poiché il centro di rotazione condilare si sposta continuamente. Questo modello aiuta a comprendere meglio la complessità dei movimenti mandibolari. | ||
Revision as of 11:45, 30 December 2024
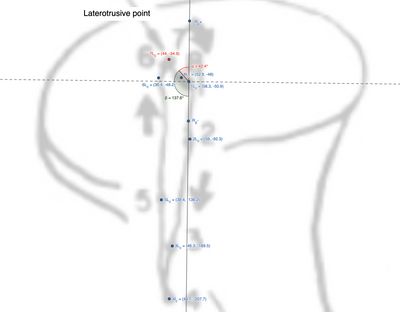
Condilo Laterotrusivo
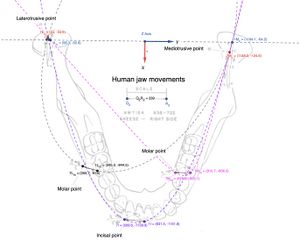
Questo paragrafo descrive il calcolo delle distanze e degli angoli tra segmenti in un piano 2D, applicati alla cinematica mandibolare. In particolare, si analizzano i movimenti articolari dei condili durante il ciclo masticatorio, rappresentati nella Figura 5 e nella Tabella 1.
| Tabella 1 | ||||
|---|---|---|---|---|
| Tracciato masticatorio | Markers | Distanza (mm) | Direzione | Direzione |
| Figura 5: Marker sovrapposti in Geogebra sul tracciato del condilo laterotrusivo | 2 | 1.734 | Protrusiva | Parallela |
| 3 | 4.99 | Protrusiva | Lateralizzazione | |
| 4 | 6.59 | Protrusiva | Lateralizzazione | |
| 5 | 3.66 | Inversione | Inversione | |
| 6 | 0.923 | Retrusiva | Lateralizzazione | |
| 7* | 0.898 | Protrusiva | Medializzazione | |
| 8 | 0.257 | Protrusiva | Medializzazione | |
Dalla figura e dalla tabella emerge che il punto rappresenta l'inversione del moto condilare, con il passaggio verso un percorso mediale diretto alla massima intercuspidazione. La distanza tra il punto e , pari a circa , definisce il movimento di Bennett.
La direzione angolare è stata calcolata come: e .
Per approfondire, il calcolo dettagliato è riportato di seguito: ![]() Calcolo dettagliato: distanza tra e , distanza euclidea , convertita in mm come , angolo .
Calcolo dettagliato: distanza tra e , distanza euclidea , convertita in mm come , angolo .
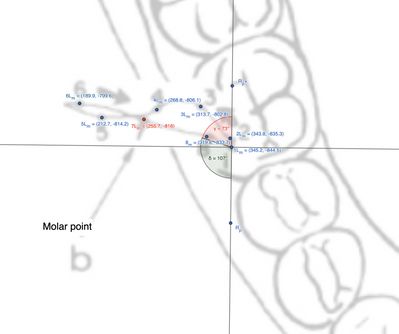
Molare Laterotrusivo
Questo paragrafo analizza i movimenti articolari del molare ipsilaterale al condilo laterotrusivo, basandosi sul calcolo delle distanze tra punti e degli angoli tra vettori mediante trigonometria vettoriale (Figura 6 e Tabella 2).
| Tabella 2 | ||||
|---|---|---|---|---|
| Tracciato masticatorio | Markers | Distanza (mm) | Direzione | Direzione dinamica |
| Figura 6: Marker grafici rilevati dal 'Replicator' durante la masticazione sul lato destro | 2 | 0.39 | Indietro | Lateralizzazione |
| 3 | 2.18 | Indietro | Lateralizzazione | |
| 4 | 3.57 | Indietro | Lateralizzazione | |
| 5 | 5.68 | Indietro | Lateralizzazione | |
| 6 | 6.76 | Indietro | Inversione | |
| 7* | 3.93 | Indietro | Medializzazione | |
| 8 | 1.15 | Indietro | Medializzazione | |
Osservando la figura e la tabella, si evidenziano le distanze e le direzioni dei punti marcati. In particolare, la distanza tra il punto e il punto iniziale è stata calcolata come circa , con un angolo tra i vettori pari a . ![]() Calcolo dettagliato:
1. Definizione dei vettori:
2. Magnitudine dei vettori:
3. Prodotto scalare:
4. Calcolo dell'angolo:
Calcolo dettagliato:
1. Definizione dei vettori:
2. Magnitudine dei vettori:
3. Prodotto scalare:
4. Calcolo dell'angolo:
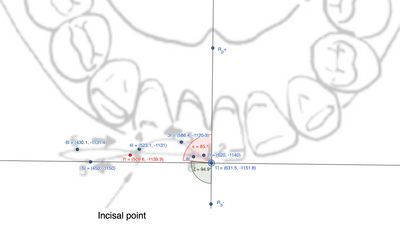
Area Incisale
Questo paragrafo analizza i movimenti articolari dell’incisivo sul lato lavorante. Utilizzando le coordinate dei punti , e in uno spazio 2D, sono calcolate le distanze lineari e l’angolo tra i segmenti che collegano questi punti.(Figura 7, tabella 3)
| Tabella 3 | ||||
|---|---|---|---|---|
| Tracciato masticatorio | Markers | Distanza (mm) | Direzione | Direzione dinamica |
| Figura 7: Markers grafici rilevati dal 'Replicator' durante la masticazione nell'area incisale sul lato destro. | 2 | 0.69 | Retrusiva | Lateralizzazione |
| 3 | 2.30 | Retrusiva | Lateralizzazione | |
| 4 | 4.61 | Retrusiva | Lateralizzazione | |
| 5 | 7.58 | Protrusiva | Lateralizzazione | |
| 6 | 8.54 | Retrusiva | Inversione | |
| 7* | 5.12 | Retrusiva | Medializzazione | |
| 8 | 1.75 | Retrusiva | Medializzazione | |
Per i tracciati dell’area incisale, la distanza tra i punti e è di , con un angolo calcolato approssimativamente pari a .
Per approfondire i calcoli, ecco la spiegazione dettagliata ![]() Calcolo dettagliato:
Coordinate dei punti: , , .
Vettori:
,
.
Norme:
,
.
Prodotto scalare:
.
Coseno dell’angolo:
.
Angolo:
.
Calcolo dettagliato:
Coordinate dei punti: , , .
Vettori:
,
.
Norme:
,
.
Prodotto scalare:
.
Coseno dell’angolo:
.
Angolo:
.
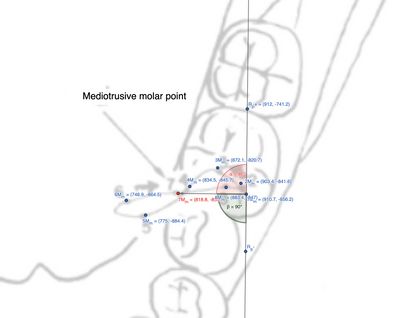
Molare mediotrusivo
L’analisi del moto cinematico mandibolare nel molare mediotrusivo evidenzia un progressivo aumento dell’angolo di direzione rispetto al molare laterotrusivo () e all’incisivo (), fino al massimo valore rilevato nel condilo (). Questo angolo, noto come angolo di svincolo mediotrusivo, si forma tra la cuspide centrale e quella distale del primo molare. La Tabella 4 e la figura 8 mostrano le distanze tra i punti del tracciato e il punto .
| Tabella 4 | ||||
|---|---|---|---|---|
| Tracciato mediotrusivo molare | Markers | Distanza (mm) | Direzione | Direzione dinamica |
| Figura 8: Markers rilevati dal 'Replicator' durante la masticazione sul lato destro. | 2 | 0.68 | Retrusiva | Medializzazione |
| 3 | 2.19 | Retrusiva | Medializzazione | |
| 4 | 3.22 | Retrusiva | Medializzazione | |
| 5 | 5.79 | Protrusiva | Medializzazione | |
| 6 | 7.22 | Protrusiva | Inversione | |
| 7* | 4.81 | Retrusiva | Lateralizzazione | |
| 8 | 1.18 | Retrusiva | Lateralizzazione | |
La distanza lineare tra il punto e è stata calcolata come , con un angolo approssimativo di . ![]() Calcolo dettagliato:
Vettori:
.
Norme:
,
.
Prodotto scalare:
.
Coseno:
.
Angolo:
.
Calcolo dettagliato:
Vettori:
.
Norme:
,
.
Prodotto scalare:
.
Coseno:
.
Angolo:
.
Condilo Mediotrusivo
Il calcolo dell’angolo tra i segmenti e è fondamentale per analizzare i movimenti articolari nel sistema masticatorio. Questa analisi consente di comprendere come si muovono i segmenti articolari rispetto a un punto di riferimento. ( Figura 9, tabella 5)
| Tabella 5 | ||||
|---|---|---|---|---|
| Tracciato masticatorio | Markers | Distanza (mm) | Direzione | Direzione |
| Figura 9: Markers rilevati dal 'Replicator' durante la masticazione sul lato destro nell'area incisale. | 2 | 2.13 | Protrusiva | Medializzazione |
| 3 | 6.19 | Protrusiva | Medializzazione | |
| 4 | 10.70 | Protrusiva | Medializzazione | |
| 5 | 11.09 | Protrusiva | Inversione | |
| 6 | 6.09 | Protrusiva | Lateralizzazione | |
| 7* | 2.61 | Protrusiva | Lateralizzazione | |
| 8 | 0.50 | Protrusiva | Lateralizzazione | |
La distanza tra il punto e è risultata , con un angolo calcolato di . Sottraendo da , si ottiene un angolo di , noto come Angolo di Bennett. Per il calcolo dettagliato ![]() Calcolo sintetico:
Vettore: , .
Prodotto scalare: .
Norme: , .
,
.
Calcolo sintetico:
Vettore: , .
Prodotto scalare: .
Norme: , .
,
.
Discussione sulla rototraslazione condilare
Il moto rototraslazionale dei condili è cruciale per comprendere la cinematica mandibolare. Se i condili ruotassero attorno a un punto fisso, i tracciati dei molari e degli incisivi sarebbero semplici archi di cerchio. Tuttavia, i movimenti reali includono sia rotazione che traslazione.
Durante la laterotrusione, il condilo ipsilaterale combina rotazione attorno all’asse verticale e traslazione laterale, mentre il condilo mediotrusivo si muove principalmente in direzione mediale e anteriore, generando il "Tragitto orbitante".
Descrizione matematica
La rototraslazione del condilo laterotrusivo può essere rappresentata come:
Dove:
- : posizione iniziale del molare ipsilaterale.
- : traslazione laterale lungo l’asse .
- : posizione finale.
Man mano che il condilo si muove, le coordinate descrivono una traiettoria ellittica proiettata su un piano 2D. Questo avviene perché il centro di rotazione istantaneo del condilo non è fisso ma si sposta continuamente.
Un fenomeno simile si osserva per il condilo mediotrusivo e gli incisivi, le cui traiettorie sono influenzate da traslazioni mediali e anteriori e da rotazioni attorno all’asse verticale. Questi tracciati non sono ellissi perfette, ma curve più complesse a causa delle variazioni nei movimenti condilari.
I tracciati dentali sono correlati ai movimenti dei condili e offrono preziose informazioni sulla cinematica mandibolare, per cui sarebbe auspicabile spendere qualche parola in più sulla velocità del moto masticatorio e la rappresentazione di questa cinematica mandibolare in un forma geometrico/matematica chiamata 'Conica'.
Velocità lineare ed angolare
Analisi del Movimento Simultaneo verso il Punto 1
Fattori Considerati
- Sincronizzazione Temporale**
Entrambi i condili devono completare il movimento di ritorno nello stesso intervallo di tempo (), indipendentemente dalla distanza percorsa.
- Differenze nelle Distanze**
- Condilo laterotrusivo (): . - Condilo mediotrusivo (): .
- Velocità di Ritorno Necessaria**
La velocità del deve essere proporzionalmente maggiore per compensare la maggiore distanza percorsa nello stesso tempo.
Calcolo della Velocità Necessaria
Assumiamo che il tempo di ritorno () sia governato dal condilo , la cui velocità media di ritorno è basata sul dato iniziale ():
Per il condilo , la velocità media necessaria () è:
Interpretazione Biomeccanica
- Velocità Significativamente Maggiore nel **
Il condilo deve operare con una velocità media di , quasi tripla rispetto a quella del (). Questo incremento è necessario per sincronizzarsi con il condilo laterotrusivo, che percorre una distanza minore nello stesso intervallo di tempo.
- Ruolo Funzionale del **
La velocità più alta del riflette il suo ruolo dinamico e adattativo. Questo condilo deve compensare: - La maggiore distanza del tragitto. - La necessità di stabilizzare il movimento mandibolare e mantenere un equilibrio biomeccanico.
- Efficienza del **
Il condilo , percorrendo una distanza più breve, opera a velocità inferiori, indicando una maggiore stabilità durante i movimenti masticatori laterali.
Conclusione
La maggiore distanza percorsa dal richiede un incremento significativo della velocità di ritorno, raggiungendo , per sincronizzarsi con il condilo . Questo fenomeno è un chiaro esempio di adattamento biomeccanico, dove la mandibola bilancia le differenze di distanza e velocità tra i due condili per garantire una chiusura armonica e simultanea.
Rappresentazione in una 'Conica'
Un modello basato su una conica passante per cinque punti strategici aiuta a rappresentare meglio queste traiettorie, come illustrato nella figura 10a.
In sintesi, i tracciati dei molari e degli incisivi assumono forme ellittiche complesse, poiché il centro di rotazione condilare si sposta continuamente. Questo modello aiuta a comprendere meglio la complessità dei movimenti mandibolari.