Lógica del lenguaje fuzzy

Other languages:

English · Italiano · Français · Deutsch · Español La traducción de esta página aún no está completa; proponga su propia traducción en la página de discusión.

En este capítulo hablaremos de la lógica difusa. Se llama difusa porque se caracteriza por la gradualidad: se puede dar a un objeto una cualidad que puede tener diversos grados de verdad.

En la primera parte de este capítulo se discutirá conceptualmente el significado de la verdad graduada, mientras que en la segunda parte nos adentraremos en el formalismo matemático introduciendo la función de pertenencia $\mu _{\displaystyle {\tilde {A}}}(x)$ es el elemento que nos permite sintetizar matemáticamente los matices de esta lógica del lenguaje. Se ha podido demostrar que con el razonamiento difuso, a diferencia de las lógicas lingüísticas anteriores, los diagnósticos muestran menos incertidumbre. Sin embargo, a pesar de ello, uno sigue sintiendo la necesidad de perfeccionar el método lingüístico y de enriquecerlo con otras "lógicas".

 

 

Introducción

Hemos llegado hasta aquí porque, como compañeros, muchas veces nos enfrentamos a responsabilidades y decisiones muy difíciles de tomar y entran en juego cuestiones como la conciencia, la inteligencia y la humildad. En tal situación, sin embargo, nos enfrentamos a dos obstáculos igualmente difíciles de manejar: el de un $KB$ (Base de conocimiento), como discutimos en el capítulo 'Lógica del lenguaje probabilístico', limitado en el tiempo que codificamos en $KB_{t}$ y uno $KB$ limitado en el contexto específico ($KB_{c}$). Estos dos parámetros de la epistemología caracterizan la era científica en la que vivimos. Además, tanto el $KB_{t}$ que el $KB_{c}$ son variables dependientes de nuestra filogenia y, en particular, de nuestra plasticidad conceptual y actitud ante el cambio.

«Yo no te entiendo»
(te doy un ejemplo practico)

• ¿Cuánta investigación se ha producido sobre el tema 'Lógica difusa'?

Pubmed responde con 2862 artículos en los últimos 10 años, por lo que podemos decir que el nuestro es actual y está suficientemente actualizado. Sin embargo, si quisiéramos centrar la atención en un tema específico como "Trastornos temporomandibulares", la base de datos responderá con hasta 2235 artículos. Por lo tanto, si quisiéramos consultar otro tema como 'Dolor orofacial', Pubmed nos brinda 1.986 artículos. Esto quiere decir que el $KB_{t}$ para estos tres temas en los últimos 10 años se ha actualizado suficientemente.

Si, ahora, quisiéramos verificar la interconexión entre los temas, notaremos que $KB_{c}$ en los contextos será el siguiente:

1. $KB_{c}=$'Trastornos temporomandibulares Y dolor orofacial'$\rightarrow$ 9 artículos en los últimos 10 años
2. $KB_{c}=$ 'Trastornos temporomandibulares Y Dolor orofacial Y Lógica difusa' 0 artículos en los últimos 10 años

El ejemplo significa que el $KB_{t}$ está relativamente actualizado individualmente para los tres temas, mientras que disminuye drásticamente cuando los temas entre contextos se fusionan y específicamente a 9 artículos para el Punto 1 e incluso a 0 artículos para el Punto 2. Entonces, el $KB_{t}$ es una variable dependiente del tiempo mientras que el $KB_{c}$ es una variable cognitiva dependiente de nuestra aptitud para el progreso de la ciencia, como ya se mencionó —entre otras cosas— en el capítulo 'Introducción'.

«casi me convences»
(Espera y verás)

Terminamos el capítulo anterior afirmando que la lógica de un lenguaje clásico y posteriormente la lógica probabilística nos han ayudado mucho en el progreso de la ciencia médica y del diagnóstico pero llevan implícitamente dentro de sí los límites de su propia lógica del lenguaje, lo que limita la visión de el universo biológico. También comprobamos que con la lógica de un lenguaje clásico —por así decirlo, Aristotélico— la sintaxis lógica que de ella se deriva en los diagnósticos de nuestra Mary Poppins limita, de hecho, la conclusión clínica.

$\{a\in x\mid \forall {\text{x}}\;A({\text{x}})\rightarrow {B}({\text{x}})\vdash A(a)\rightarrow B(a)\}$ (ver capítulo Lógica del lenguaje clásico),

sostiene que: "todo paciente normal $\forall {\text{x}}$ que es positivo en el examen radiográfico de la ATM $\mathrm {\mathcal {A}} ({\text{x}})$ tiene TTM $\rightarrow \mathrm {\mathcal {B}} ({\text{x}})$, como consecuencia directa $\vdash$ Mary Poppins es positiva (y además es una paciente "normal") en la radiografía de la ATM $A(a)$ entonces Mary Poppins también está afectada por los TTM $\rightarrow {\mathcal {B}}(a)$

La limitación del camino lógico seguido nos ha llevado a emprender un camino alternativo, en el que se evita el carácter bivalente o binario de la lógica del lenguaje clásico y se sigue un modelo probabilístico. El colega dentista, de hecho, cambió el vocabulario y prefirió una conclusión como:

$P(D|Deg.TMJ\cap TMDs)=0.95$

y es que nuestra Mary Poppins está afectada en un 95% por TTM ya que tiene una degeneración de la articulación temporomandibular avalada por la positividad del dato $D=\{\delta _{1},\dots \delta _{4}\}$ en una muestra poblacional 0. Sin embargo, también encontramos que en el proceso de construcción de la lógica probabilística (Analysandum $=\{P(D),a\}$) que nos permitió formular las mencionadas conclusiones del diagnóstico diferencial y elegir la más plausible, existe un elemento crucial para todo el Analysand $=\{\pi ,a,KB\}$ representado por el término $KB$ que indica, en concreto, una 'Base de Conocimiento' del contexto sobre la que se construye la lógica del lenguaje probabilístico.

Por lo tanto, llegamos a la conclusión de que tal vez el colega dentista debería haberse dado cuenta de su propia 'incertidumbre subjetiva' (¿afectada por TMD o _nOP?) e 'incertidumbre objetiva' (¿probablemente más afectada por TMD o _nOP?).

• ¿Por qué hemos llegado a estas conclusiones críticas?

Por una forma ampliamente compartida de representación de la realidad, sustentada en el testimonio de figuras autorizadas que confirman su criticidad. Esto ha dado lugar a una visión de la realidad que, a primera vista, parecería inadecuada para el lenguaje médico; de hecho, expresiones como “alrededor de 2” o “moderadamente” pueden suscitar legítima perplejidad y parecer un retorno anacrónico a conceptos precientíficos. Sin embargo, por el contrario, el uso de números borrosos o afirmaciones permite tratar los datos científicos en contextos en los que no se puede hablar de “probabilidad” sino solo de “posibilidad”.

«¿Probabilidad o Posibilidad?»

Fuzzy truth

En el ambicioso intento de traducir matemáticamente la racionalidad humana, se pensó a mediados del siglo XX en ampliar el concepto de lógica clásica formulando la lógica difusa. La lógica difusa se refiere a las propiedades que podríamos llamar de “gradualidad”, es decir, que se le pueden atribuir a un objeto con diferentes grados. Algunos ejemplos son las propiedades 'estar enfermo', 'tener dolor', 'ser alto', 'ser joven', etc.

Matemáticamente, la lógica difusa nos permite atribuir a cada proposición un grado de verdad entre $0$ y $1$. El ejemplo más clásico para explicar este concepto es el de la edad: podemos decir que un recién nacido tiene un ‘grado de juventud’ igual a $1$, un joven de dieciocho años igual a $0,8$, un sexagenario igual a $0,4$, etcétera

En el contexto de la lógica clásica, por otro lado, las declaraciones:

• un niño de diez años es joven
• un treintañero es joven

ambos son verdaderos. Sin embargo, en el caso de la lógica clásica (que sólo admite los dos datos verdadero o falso), esto significaría que el infante y el treintañero son igualmente jóvenes. Lo cual obviamente está mal.

La importancia y el encanto de la lógica difusa surgen del hecho de que es capaz de traducir la incertidumbre inherente a algunos datos del lenguaje humano en formalismo matemático, codificando conceptos 'elásticos' (como casi alto, bastante bueno, etc.), en para hacerlos comprensibles y manejables por las computadoras.

Teoría de conjuntos

Como se mencionó en el capítulo anterior, el concepto básico de la lógica difusa es el de multivalencia, es decir, en términos de teoría de conjuntos, de la posibilidad de que un objeto pueda pertenecer a un conjunto aunque sea parcialmente y, por lo tanto, también a varios conjuntos con diferentes grados. . Recordemos desde el principio los elementos básicos de la teoría de los conjuntos ordinarios. Como se verá, en ellos aparecen las expresiones formales de los principios de la lógica aristotélica, recordados en el capítulo anterior.

Cuantificadores

• Membresía: representado por el símbolo $\in$ (pertenece), - por ejemplo, el número 13 pertenece al conjunto de números impares$\in$ $13\in Odd$
• No pertenencia: representado por el símbolo $\notin$ (No pertenece)
• Inclusión: Representado por el símbolo $\subset$ (es contenido), - por ejemplo, el $A$ completo está contenido dentro del conjunto más grande $U$, $A\subset U$ (en este caso se dice que $A$ es un subconjunto de $U$)
• Cuantificador universal, que se indica con el símbolo $\forall$ (para cada uno)
• Demostración, que se indica con el símbolo $\mid$ (tal que)

Establecer operadores

Dado todo el universo $U$ indicamos con $x$ su elemento genérico de modo que $x\in U$; entonces, consideramos dos subconjuntos $A$ y $B$ interna a $U$ de modo que $A\subset U$ y $B\subset U$

	Unión: representado por el símbolo $\cup$, indica la unión de los dos conjuntos $A$ y $B$ $(A\cup B)$. Está definido por todos los elementos que pertenecen a $A$ y $B$ o ambos: $(A\cup B)=\{\forall x\in U\mid x\in A\land x\in B\}$
	Intersección: representado por el símbolo$\cap$, indica los elementos pertenecientes a ambos conjuntos: $(A\cap B)=\{\forall x\in U\mid x\in A\lor x\in B\}$
	Diferencia:representado por el símbolo $-$, Por ejemplo $A-B$ muestra todos los elementos de $A$ excepto los compartidos con $B$
	Complementaria: representado por una barra sobre el nombre de la colección, indica por ${\bar {A}}$ La complementaria de $A$,es decir, el conjunto de elementos que pertenecen a todo el universo excepto los de $A$, en fórmulas:${\bar {A}}=U-A$

La teoría de la lógica del lenguaje difuso es una extensión de la teoría clásica de conjuntos en la que, sin embargo, los principios de no contradicción y del tercero excluido no son válidos. Recuérdese que en lógica clásica, dado el conjunto $A$ y su ${\bar {A}}$ complementario, el principio de no contradicción establece que si un elemento pertenece al $A$ entero no puede a la vez pertenecer también a su ${\bar {A}}$ complementario; según el principio del tercero excluido, sin embargo, la unión de un $A$ entero y su ${\bar {A}}$ complementario constituye el universo completo $U$

En otras palabras, si algún elemento no pertenece al todo, necesariamente debe pertenecer a su complementario.

Conjunto difuso ${\tilde {A}}$ y función de pertenencia $\mu _{\displaystyle {\tilde {A}}}(x)$

Elegimos, como formalismo, representar un conjunto borroso con la 'tilde': ${\tilde {A}}$ Un conjunto borroso es un conjunto donde los elementos tienen un 'grado' de pertenencia (de acuerdo con la lógica borrosa): algunos pueden incluirse en el conjunto en 100%, otros en porcentajes menores.

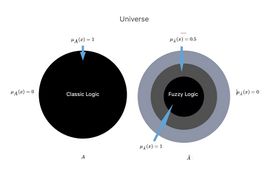
Para representar matemáticamente este grado de pertenencia se encuentra la función $\mu _{\displaystyle {\tilde {A}}}(x)$ denominada 'Función de pertenencia'. La función $\mu _{\displaystyle {\tilde {A}}}(x)$ es una función continua definida en el intervalo $[0;1]$ donde es:

• $\mu _{\tilde {A}}(x)=1\rightarrow$ si $x$ está totalmente contenido en $A$ (estos puntos se llaman 'núcleo', indican valores predicados plausibles).
• $\mu _{\tilde {A}}(x)=0\rightarrow$si $x$ no está contenido en $A$
• $0<\mu _{\tilde {A}}(x)<1\;\rightarrow$si $x$ está parcialmente contenido en $A$ (estos puntos se llaman 'soporte', indican los posibles valores predicados).

La representación gráfica de la función $\mu _{\displaystyle {\tilde {A}}}(x)$ puede ser variado; desde los de líneas lineales (triangulares, trapezoidales) hasta los que tienen forma de campana o 'S' (sigmoidales) como se muestra en la Figura 1, que contiene todo el concepto gráfico de la función de pertenencia....

Figure 1: Types of graphs for the membership function.

El conjunto soporte de un conjunto borroso se define como la zona en la que el grado de pertenencia resulta $0<\mu _{\tilde {A}}(x)<1$; por su parte, el núcleo se define como el ámbito en el que el grado de pertenencia asume el valor $\mu _{\tilde {A}}(x)=1$

El 'Conjunto de soporte' representa los valores del predicado que se consideran posibles, mientras que el 'núcleo' representa los que se consideran más plausibles.

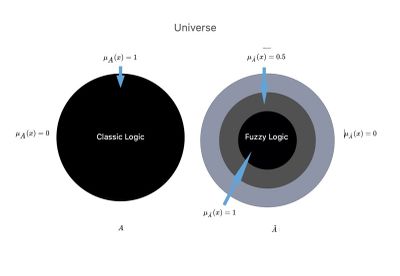
Si ${A}$ representara un conjunto en el sentido ordinario del término o en la lógica del lenguaje clásico descrita anteriormente, su función de pertenencia podría asumir solo los valores $1$ o $0$, $\mu _{\displaystyle {A}}(x)=1\;\lor \;\mu _{\displaystyle {A}}(x)=0$ finalizando en si el elemento $x$ pertenece o no al todo, según se considere. La Figura 2 muestra una representación gráfica del concepto nítido (rígidamente definido) o confuso de membresía, que recuerda claramente las consideraciones de Smuts.

Volvamos al caso concreto de nuestra Mary Poppins, en el que vemos una discrepancia entre las afirmaciones del dentista y del neurólogo y buscamos una comparación entre la lógica clásica y la lógica difusa:

Figure 2: Representation of the comparison between a classical and fuzzy ensemble.

Figura 2: Imaginemos el Universo de la Ciencia $U$ en el que existen dos mundos o contextos paralelos, el ${A}$ y el ${\tilde {A}}$

${A}=$ En el contexto científico, el llamado ‘crisp’, y lo hemos convertido a la lógica del Lenguaje Clásico, en el que el médico dispone de una información científica absoluta $KB$ con una clara línea divisoria que hemos denominado $KB_{c}$

${\tilde {A}}=$ En otro contexto científico llamado ‘lógica difusa’, y en el que existe una unión entre el subconjunto ${A}$ en ${\tilde {A}}$ que podemos llegar a decir: unión entre $KB_{c}$

Notaremos notablemente las siguientes deducciones:

• Lógica Clásica en el Contexto Odontológico ${A}$ en el que sólo será posible un proceso lógico que dé como resultado $\mu _{\displaystyle {A}}(x)=1$, o siendo $\mu _{\displaystyle {A}}(x)=0$ el rango de datos $D=\{\delta _{1},\dots ,\delta _{4}\}$ reducido a conocimientos básicos $KB$ en el conjunto ${A}$. Esto quiere decir que fuera del mundo odontológico existe un void y ese término de la teoría de conjuntos se escribe precisamente $\mu _{\displaystyle {A}}(x)=0$ y que es sinónimo de un rango alto de:

«Error de diagnóstico diferencial»

• Lógica difusa en un contexto dental ${\tilde {A}}$ en el que se representan más allá de los conocimientos básicos $KB$ del contexto dental también aquellos parcialmente adquiridos del mundo neurofisiológico $0<\mu _{\tilde {A}}(x)<1$ tendrán la prerrogativa de devolver un resultado $\mu _{\tilde {A}}(x)=1$ y un resultado $0<\mu _{\tilde {A}}(x)<1$ debido a conocimientos básicos $KB$ que en este punto está representado por la unión de $KB_{c}$ contextos dentales y neurológicos. El resultado de esta implementación científico-clínica de la odontología permitiría una
  «Reducción del error de diagnóstico diferencial»

Final considerations

Topics that could distract the reader’s attention were, in fact, essential for demonstrating the message. Normally, indeed, when any more or less brilliant mind allows itself to throw a stone into the pond of Science, a shockwave is generated, typical of the period of Kuhn’s extraordinary science, against which most of the members of the international scientific community row. With good faith, we can say that this phenomenon—as regards the topics we are addressing here—is well represented in the premise at the beginning of the chapter.

In these chapters, actually, a fundamental topic for science has been approached: the re-evaluation, the specific weight that has always been given to $P-value$, awareness of scientific / clinical contexts $KB_{c}$, having undertaken a more elastic path of Fuzzy Logic than the Classical one, realizing the extreme importance of $KB$ and ultimately the union of contexts $KB_{c}$ to increase its diagnostic capacity.

In the next chapter we will be ready to undertake an equally fascinating path: it will leads us to the context of a System Language logic, and will allow us to deepen our knowledge, no longer in clinical semeiotics only, but in the understanding of system functions (recently it is being evaluated in neuromotor disciplines for Parkinson's disease).In Masticationpedia, of course, we will report the topic 'System Inference' in the field of the masticatory system as we could read in the next chapter entitled 'System logic'.

Bibliography & references

Masticationpedia is a charity, a not-for-profit organization operating in dentistry medical research,
particularly focusing on the field of the neurophysiology of the masticatory system
 

Home

Introduction

Latest chapter

Ed. Lab

Donate

Contacts