Fuzzy logic language/it

In questo capitolo parleremo della logica fuzzy. Si chiama fuzzy perché è caratterizzata da una gradualità: ad un oggetto si può attribuire una qualità che può avere vari gradi di verità.

Nella prima parte di questo capitolo, verrà discusso concettualmente il significato della verità graduata, mentre nella seconda parte, ci addentreremo nel formalismo matematico introducendo la funzione di appartenenza $\mu _{\displaystyle {\tilde {A}}}(x)$: l'elemento che ci permette di sintetizzare matematicamente le sfumature di questa logica del linguaggio. È stato possibile dimostrare che con il ragionamento 'fuzzy', a differenza delle precedenti logiche del linguaggio, le diagnosi mostrano meno incertezza. Nonostante questo, però, si sente ancora la necessità di raffinare ulteriormente il metodo linguistico e di arricchirlo con altre 'logiche'.. 

 

Introduzione

Siamo arrivati a questo punto perché, come colleghi, ci troviamo molto spesso di fronte a responsabilità e decisioni che sono molto difficili da prendere e entrano in gioco questioni come la coscienza, l'intelligenza e l'umiltà. In tale situazione, però, ci troviamo di fronte a due ostacoli ugualmente difficili da gestire: quello di una $KB$ (Knowledge Basis, base di Conoscenza), come l'abbiamo discussa nel capitolo 'Logica del linguaggio probabilistico', limitata nel tempo che codifichiamo in $KB_{t}$, e una $KB$ limitata nel contesto specifico ($KB_{c}$). Questi due parametri dell'epistemologia caratterizzano l'epoca scientifica in cui viviamo. Inoltre, sia la $KB_{t}$ che la $KB_{c}$ sono variabili dipendenti della nostra filogenesi e, in particolare, della nostra plasticità concettuale e attitudine al cambiamento.

«I'm not following you»
(I'll give you a practical example)

• Quante ricerche sono state prodotte sull'argomento "logica fuzzy"?

Pubmed risponde con 2862 articoli negli ultimi 10 anni, così che possiamo dire che il nostro è attuale ed è sufficientemente aggiornato. Tuttavia, se volessimo focalizzare l'attenzione su un argomento specifico come 'Disturbi Temporomandibolari', il database risponderà con ben 2.235 articoli. Quindi, se volessimo controllare un altro argomento come 'Orofacial Pain', Pubmed ci dà 1.986 articoli. Questo significa che il $KB_{t}$ per questi tre argomenti negli ultimi 10 anni è stato sufficientemente aggiornato.

Se, ora, volessimo verificare l'interconnessione tra gli argomenti, noteremo che $KB_{c}$ nei contesti sarà il seguente:

1. $KB_{c}=$ 'Disturbi temporomandibolari E dolore orofacciale'$\rightarrow$ 9 articoli negli ultimi 10 anni
2. $KB_{c}=$ 'Disturbi temporomandibolari E Dolore orofacciale E Logica fuzzy' 0 articoli negli ultimi 10 anni

L'esempio indica che il $KB_{t}$ è relativamente aggiornato individualmente per i tre argomenti, mentre diminuisce drasticamente quando gli argomenti tra i contesti sono uniti e specificamente a 9 articoli per il punto 1 e anche a 0 articoli per il punto 2. So, the $KB_{t}$ is a time dependent variable while the $KB_{c}$ is a cognitive variable dependent on our aptitude for the progress of science, as already mentioned—among other things—in the chapter ‘Introduction’.

«mi hai quasi convinto»
(Aspetta e vedrai)

Abbiamo concluso il capitolo precedente affermando che la logica di un linguaggio classico e successivamente la logica probabilistica ci hanno aiutato molto nel progresso della scienza medica e della diagnostica, ma implicitamente portano in sé i limiti della propria logica di linguaggio, che limita la visione dell'universo biologico. Abbiamo anche verificato che con la logica di un linguaggio classico, per così dire aristotelico, la sintassi logica che ne deriva nella diagnostica della nostra Mary Poppins limita, di fatto, la conclusione clinica.

$\{a\in x\mid \forall {\text{x}}\;A({\text{x}})\rightarrow {B}({\text{x}})\vdash A(a)\rightarrow B(a)\}$ (vedi capitolo Classical Language's Logic),

afferma che: "qualsiasi paziente normale $\forall {\text{x}}$ che è positivo all'esame radiografico del TMJ $\mathrm {\mathcal {A}} ({\text{x}})$ ha dei TMD$\rightarrow \mathrm {\mathcal {B}} ({\text{x}})$, come diretta conseguenza $\vdash$ Essendo Mary Poppins positiva (ed essendo anche una paziente "normale") sulla radiografia del TMJ $A(a)$, allora anche Mary Poppins è affetta da TMD $\rightarrow {\mathcal {B}}(a)$

La limitazione del percorso logico seguito ci ha portato a intraprendere un percorso alternativo, in cui si evita la bivalenza o la natura binaria della logica linguistica classica e si segue un modello probabilistico. Il collega dentista, infatti, ha cambiato il vocabolario e ha preferito una conclusione come:

$P(D|Deg.TMJ\cap TMDs)=0.95$

e cioè che la nostra Mary Poppins è affetta al 95% da TMD poiché ha una degenerazione dell'articolazione temporomandibolare sostenuta dalla positività dei dati $D=\{\delta _{1},\dots \delta _{4}\}$ in un campione di popolazione $n$. However, we also found that in the process of constructing probabilistic logic (Analysandum $=\{P(D),a\}$) which allowed us to formulate the aforementioned differential diagnostic conclusions and choose the most plausible one, there is a crucial element to the whole Analysand$=\{\pi ,a,KB\}$ represented by the term $KB$ which indicates, specifically, a 'Knowledge Base' of the context on which the logic of probabilistic language is built.

We therefore concluded that perhaps the dentist colleague should have become aware of his own 'Subjective Uncertainty' (affected by TMDs or _nOP?) and 'Objective Uncertainty' (probably more affected by TMDs or _nOP?).

• Perché siamo arrivati a queste conclusioni critiche?

Per una forma ampiamente condivisa di rappresentazione della realtà, sostenuta dalla testimonianza di figure autorevoli che ne confermano la criticità. Questo ha dato origine a una visione della realtà che, a prima vista, sembrerebbe inadatta al linguaggio medico; infatti, espressioni come "circa 2" o "moderatamente" possono suscitare legittime perplessità e sembrare un anacronistico ritorno a concetti pre-scientifici. Al contrario, però, l'uso dei numeri fuzzy o delle asserzioni permette di trattare i dati scientifici in contesti in cui non si può parlare di 'probabilità' ma solo di 'possibilità'.

«Probabilità o possibilità?»

Verità fuzzy

Nell'ambizioso tentativo di tradurre in matematica la razionalità umana, si è pensato a metà del XX secolo di espandere il concetto di logica classica formulando la logica fuzzy. La logica fuzzy riguarda le proprietà che potremmo chiamare 'gradualità', cioè che possono essere attribuite a un oggetto con gradi diversi. Esempi sono le proprietà 'essere malato', 'avere dolore', 'essere alto', 'essere giovane', e così via.

Tradotto con www.DeepL.com/Translator (versione gratuita)

Mathematically, fuzzy logic allows us to attribute to each proposition a degree of truth between $0$ and $1$. The most classic example to explain this concept is that of age: we can say that a new-born has a ‘degree of youth’ equal to $1$, an eighteen-year-old equal to $0,8$, a sixty-year-old equal to $0,4$, and so on

Nel contesto della logica classica, invece, le affermazioni:

• • un bambino di dieci anni è giovane
  • un trentenne è giovane

sono entrambe vere. Tuttavia, nel caso della logica classica (che ammette solo i due dati vero o falso), questo significherebbe che il bambino e il trentenne sono ugualmente giovani. Il che è ovviamente sbagliato.

L'importanza e il fascino della logica fuzzy derivano dal fatto che è in grado di tradurre l'incertezza insita in alcuni dati del linguaggio umano in un formalismo matematico, codificando concetti 'elastici' (come quasi alto, abbastanza buono, ecc.), al fine di renderli comprensibili e gestibili dai computer.

Teoria degli insiemi

Come accennato nel capitolo precedente, il concetto base della logica fuzzy è quello della multivalenza, cioè, in termini di teoria degli insiemi, della possibilità che un oggetto possa appartenere a un insieme anche solo parzialmente e, quindi, anche a più insiemi con gradi diversi. Ricordiamo fin dall'inizio gli elementi di base della teoria degli insiemi ordinari. Come si vedrà, in essi appaiono le espressioni formali dei principi della logica aristotelica, ricordati nel capitolo precedente.

Quantificatori

• Appartenenza: rappresentato dal simbolo $\in$ (appartiene), - per esempio il numero 13 appartiene all'insieme dei numeri dispari $\in$ $13\in Odd$
• Non appartenenza: rappresentato dal simbolo $\notin$ (Non appartiene)
• Inclusione: Represented by the symbol $\subset$ (is content), - for example the whole $A$ it is contained within the larger set $U$, $A\subset U$ (in this case it is said that $A$ is a subset of $U$)
• Quantificatore universale, which is indicated by the symbol $\forall$ (for each)
• Dimostrazione, which is indicated by the symbol $\mid$ (such that)

Set operators

Given the whole universe $U$ we indicate with $x$ its generic element so that $x\in U$; then, we consider two subsets $A$ and $B$ internal to $U$ cosicché $A\subset U$ e $B\subset U$

	Unione: represented by the symbol $\cup$, indicates the union of the two sets $A$ e $B$ $(A\cup B)$. It is defined by all the elements that belong to $A$ e $B$ or both: $(A\cup B)=\{\forall x\in U\mid x\in A\land x\in B\}$
	Intersezione: represented by the symbol $\cap$, indicates the elements belonging to both sets: $(A\cap B)=\{\forall x\in U\mid x\in A\lor x\in B\}$
	Differenza: represented by the symbol $-$, per esempio $A-B$ shows all elements of $A$ except those shared with $B$
	Complementary: represented by a bar above the name of the collection, it indicates by ${\bar {A}}$ the complementary of $A$, cioè, the set of elements that belong to the whole universe except those of $A$, in formule: ${\bar {A}}=U-A$

The theory of fuzzy language logic is an extension of the classical theory of sets in which, however, the principles of non-contradiction and the excluded third are not valid. Remember that in classical logic, given the set $A$ and its complementary ${\bar {A}}$, the principle of non-contradiction states that if an element belongs to the whole $A$ it cannot at the same time also belong to its complementary ${\bar {A}}$; according to the principle of the excluded third, however, the union of a whole $A$ and its complementary ${\bar {A}}$ constitutes the complete universe $U$.

In other words, if any element does not belong to the whole, it must necessarily belong to its complementary.

Fuzzy set ${\tilde {A}}$ and membership function $\mu _{\displaystyle {\tilde {A}}}(x)$

We choose - as a formalism - to represent a fuzzy set with the 'tilde':${\tilde {A}}$. A fuzzy set is a set where the elements have a 'degree' of belonging (consistent with fuzzy logic): some can be included in the set at 100%, others in lower percentages.

To mathematically represent this degree of belonging is the function $\mu _{\displaystyle {\tilde {A}}}(x)$ called 'Membership Function'. The function $\mu _{\displaystyle {\tilde {A}}}(x)$ is a continuous function defined in the interval $[0;1]$where it is:

• $\mu _{\tilde {A}}(x)=1\rightarrow$ if $x$ is totally contained in $A$ (these points are called 'nucleus', they indicate plausible predicate values).
• $\mu _{\tilde {A}}(x)=0\rightarrow$ if $x$ is not contained in $A$
• $0<\mu _{\tilde {A}}(x)<1\;\rightarrow$ if $x$ is partially contained in $A$ (these points are called 'support', they indicate the possible predicate values).

The graphical representation of the function $\mu _{\displaystyle {\tilde {A}}}(x)$ it can be varied; from those with linear lines (triangular, trapezoidal) to those in the shape of bells or 'S' (sigmoidal) as depicted in Figure 1, which contains the whole graphic concept of the function of belonging.

Figure 1: Types of graphs for the membership function.

The support set of a fuzzy set is defined as the zone in which the degree of membership results $0<\mu _{\tilde {A}}(x)<1$; on the other hand, the core is defined as the area in which the degree of belonging assumes value $\mu _{\tilde {A}}(x)=1$

The 'Support set' represents the values of the predicate deemed possible, while the 'core' represents those deemed more plausible.

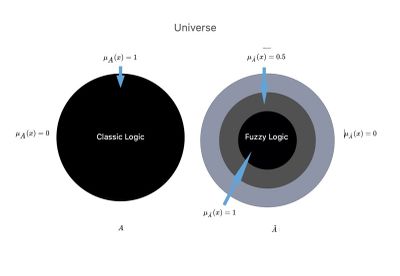
If ${A}$ represented a set in the ordinary sense of the term or classical language logic previously described, its membership function could assume only the values $1$ or $0$, $\mu _{\displaystyle {A}}(x)=1\;\lor \;\mu _{\displaystyle {A}}(x)=0$ depending on whether the element $x$ whether or not it belongs to the whole, as considered. Figure 2 shows a graphic representation of the crisp (rigidly defined) or fuzzy concept of membership, which clearly recalls Smuts's considerations.

Let us go back to the specific case of our Mary Poppins, in which we see a discrepancy between the assertions of the dentist and the neurologist and we look for a comparison between classical logic and fuzzy logic:

Figure 2: Representation of the comparison between a classical and fuzzy ensemble.

Figure 2: Let us imagine the Science Universe $U$ in which there are two parallel worlds or contexts, ${A}$ and ${\tilde {A}}$.

${A}=$ In the scientific context, the so-called ‘crisp’, and we have converted into the logic of Classic Language, in which the physician has an absolute scientific background information $KB$ with a clear dividing line that we have named $KB_{c}$.

${\tilde {A}}=$ In another scientific context called ‘fuzzy logic’, and in which there is a union between the subset ${A}$ in ${\tilde {A}}$ that we can go so far as to say: union between $KB_{c}$.

We will remarkably notice the following deductions:

• Classical Logic in the Dental Context ${A}$ in which only a logical process that gives as results $\mu _{\displaystyle {A}}(x)=1$ it will be possible, or $\mu _{\displaystyle {A}}(x)=0$ being the range of data $D=\{\delta _{1},\dots ,\delta _{4}\}$reduced to basic knowledge $KB$ in the set ${A}$. This means that outside the dental world there is a void and that term of set theory, it is written precisely $\mu _{\displaystyle {A}}(x)=0$ and which is synonymous with a high range of:

«Differential diagnostic error»

• Fuzzy logic in a dental context ${\tilde {A}}$ in which they are represented beyond the basic knowledge $KB$ of the dental context also those partially acquired from the neurophysiological world $0<\mu _{\tilde {A}}(x)<1$ will have the prerogative to return a result $\mu _{\tilde {A}}(x)=1$ and a result $0<\mu _{\tilde {A}}(x)<1$ because of basic knowledge $KB$ which at this point is represented by the union of $KB_{c}$ dental and neurological contexts. The result of this scientific-clinical implementation of dentistry would allow a:
  «Reduction of differential diagnostic error»

Final considerations

Topics that could distract the reader’s attention—was, in fact, essential for demonstrating the message. Normally, in fact, when any more or less brilliant mind allows itself to throw a stone into the pond of Science, a shockwave is generated, typical of the period of Kuhn’s extraordinary science, against which most of the members of the international scientific community row. With good faith, we can say that this phenomenon—as regards the topics we are addressing here—is well represented in the premise at the beginning of the chapter.

In these chapters, in fact, a fundamental topic for science has been approached: the re-evaluation, the specific weight that has always been given to $P-value$, awareness of scientific / clinical contexts $KB_{c}$, having undertaken a more elastic path of Fuzzy Logic than the Classical one, realizing the extreme importance of $KB$ and ultimately the union of contexts $KB_{c}$ to increase its diagnostic capacity.

In the next chapter we will be ready to undertake an equally fascinating path that will leads us to the context of a System Language logic and will allow us to deepen our knowledge no longer only in clinical semeiotics but in the understanding of system functions as recently it is approaching in neuromotor disciplines for Parkinson's disease. In Masticationpedia, of course, we will report the topic 'System Inference' in the field of the masticatory system as we could read in the next chapter entitled 'System logic'.

 

The logic of probabilistic language   Introduction

Bibliography & references

Masticationpedia is a charity, a not-for-profit organization operating in dentistry medical research,
particularly focusing on the field of the neurophysiology of the masticatory system
 

Home

Introduction

Latest chapter

Ed. Lab

Donate

Contacts