Difference between revisions of "Bilateral Trigeminal neuromotor organic symmetry"
Gianfranco (talk | contribs) |
|||
| (18 intermediate revisions by one other user not shown) | |||
| Line 4: | Line 4: | ||
[[File:Potenziale Evocato della Radice Trigeminale.jpg | [[File:Potenziale Evocato della Radice Trigeminale.jpg|left]] | ||
In order to achieve a complete clinical evaluation of mastication, an in-depth neurophysiopathological assessment of masticatory muscles control is required. Electromyography technique (EMG) is widely used for this purpose, but failed to provide convincing results. | <translate>In order to achieve a complete clinical evaluation of mastication, an in-depth neurophysiopathological assessment of masticatory muscles control is required. Electromyography technique (EMG) is widely used for this purpose, but failed to provide convincing results</translate>. | ||
<translate>The aim of this work was to describe our quantitative objectivation of the motor control of the masticatory muscles and to verify the hypothesis to consider the bilateral Root Motor Evoked Potentials as an electrophysiological normalization factor</translate>. | |||
{{ArtBy| | {{ArtBy| | ||
| autore = Gianni Frisardi | | autore = Gianni Frisardi | ||
| autore2 = | | autore2 = Şükrü Okkesim | ||
| autore3 = | | autore3 = Alice Bisirri | ||
| autore4 = | | autore4 = Flavio Frisardi | ||
| autore5 = | | autore5 = Pier Paolo Valentini | ||
| autore6 = | | autore6 = | ||
}} | }} | ||
| Line 206: | Line 199: | ||
===Statistical analysis=== | ===Statistical analysis=== | ||
The statistical analysis follows a conventional process aimed at the quantification of the “ <math>_mANEE</math> ”, which essentially indicates the maximum absolute value delivered by the motor trigeminal nervous system and an unconventional process focused mainly on the symmetry analysis between the sides of the bR-MEPs. | The statistical analysis follows a conventional process aimed at the quantification of the “<math>_mANEE</math> ”, which essentially indicates the maximum absolute value delivered by the motor trigeminal nervous system and an unconventional process focused mainly on the symmetry analysis between the sides of the bR-MEPs. | ||
[[File:Symmetry 1.jpg|sinistra|thumb|377px|'''Table 1:''' shows the raw EMG values for the onset latency, amplitude and integral area of the bR-MEPs. (*) Indicates EMGvalues of the subject considered as example in results section.]] | [[File:Symmetry 1.jpg|sinistra|thumb|377px|'''Table 1:''' shows the raw EMG values for the onset latency, amplitude and integral area of the bR-MEPs. (*) Indicates EMGvalues of the subject considered as example in results section.]] | ||
We performed descriptive statistic on the raw EMG values for the computation of mean, standard deviations, analysis of sample’s distribution. The comparison between the two sides for the latencies, amplitudes and EMG integral areas was performed by Kruskal-Wallis test. | We performed descriptive statistic on the raw EMG values for the computation of mean, standard deviations, analysis of sample’s distribution. The comparison between the two sides for the latencies, amplitudes and EMG integral areas was performed by Kruskal-Wallis test. | ||
| Line 212: | Line 205: | ||
Significance was set at a <math>p-value <0.05</math>''p''. | Significance was set at a <math>p-value <0.05</math>''p''. | ||
=== | ===Artificial neural network model=== | ||
An artificial neural network (ANN) is a general mathematical computing paradigm by which the geometry and functionality of the ANN have been linked to the biological neural system and one of the most interesting characteristic of this paradigm is the self-learning propriety. | An artificial neural network (ANN) is a general mathematical computing paradigm by which the geometry and functionality of the ANN have been linked to the biological neural system and one of the most interesting characteristic of this paradigm is the self-learning propriety. | ||
The ANN computational model has been used to estimate the correlation coefficient with the EMG values of one side. With the ANNs, we can determine the correlations that describe input/output formulation in a dataset or a system. <ref name=":5" /><ref name=":6" /> | The ANN computational model has been used to estimate the correlation coefficient with the EMG values of one side. With the ANNs, we can determine the correlations that describe input/output formulation in a dataset or a system.<ref name=":5" /><ref name=":6" /> | ||
If organic symmetry exists, there would be a correlation coefficient between the EMG values of the right and left muscles. To test this assumption, we adopted the ANN model. First we created, configured, and initialized our multi-layer ANN.<ref name=":6" /> | If organic symmetry exists, there would be a correlation coefficient between the EMG values of the right and left muscles. To test this assumption, we adopted the ANN model. First we created, configured, and initialized our multi-layer ANN.<ref name=":6" /> | ||
We assumed that each layer is composed of a number of predefined neurons. The neurons in the input layer perform as a buffer which | ====The multi-layer ANN==== | ||
We assumed that each layer is composed of a number of predefined neurons. <br />The neurons in the input layer perform as a buffer which divides into portions and dispense the input signals <math>x_i</math> to the next neurons in the hidden layer without degrading the signal. Each neuron <math>j</math> in the hidden layer sums the input signals <math>x_i</math>, after weighting them with the strengths <math>w_{i,j}</math> of the respective connections from the input layer, and calculates its output <math>y_i</math> as a function <math>f</math> of the sum.<blockquote><math>y_j=\sum_{i=1}^N w_jx_i</math> <math>Eq.1</math></blockquote> | |||
Where, <math>w_{i,j}</math> is the weight of the ''<math>i^{th}</math>'' and ''<math>j^{th}</math>'' connection and ''<math>x_i</math>'' is the ''<math>i^{th}</math>'' input signal. <math>f</math> is the activation function which is needed to transform the weighted sum of all signals influencing a neuron.<ref name=":5">Akdenur B, Okkesum S, Kara S, Gunes S (2009) Correlation- and covariance- supported normalization method for estimating orthodontic trainer treatment for clenching activity. Proc Inst Mech Eng H 223: 991-1001.</ref> | Where, <math>w_{i,j}</math> is the weight of the ''<math>i^{th}</math>'' and ''<math>j^{th}</math>'' connection and ''<math>x_i</math>'' is the ''<math>i^{th}</math>'' input signal. <math>f</math> is the activation function which is needed to transform the weighted sum of all signals influencing a neuron.<ref name=":5">Akdenur B, Okkesum S, Kara S, Gunes S (2009) Correlation- and covariance- supported normalization method for estimating orthodontic trainer treatment for clenching activity. Proc Inst Mech Eng H 223: 991-1001.</ref> | ||
In our ANN model, | In our ANN model, a radial basis function (RBF) has been chosen as the activation function <math>f</math>. In the field of mathematical modelling, an artificial neural network that uses RBF as activation function is properly called a 'radial basis function network'. The output of this network is a linear combination of RBF of the inputs and neuron parameters. RBF has many application, and we choose this one because it is specific for function approximation tasks. | ||
====Algorithms and network==== | |||
We decided to initialize two layers and define ten neurons in the hidden layer in order to increase the power of our network. We equipped our ANN with the Levenberg-Marquardt (LM) algorithm as training function to be used and trained with the normalized features computed from the EMG of the left muscles. With the LM algorithm, we were able to achieve the rapid execution of the network.<ref name=":6">Kara S, Dirgenali F, Okkesim S (2006) Detection of gastric dysrhythmia using WT and ANN in diabetic gastroparesis patients. Comput Biol Med 36: 276-290.</ref> | We decided to initialize two layers and define ten neurons in the hidden layer in order to increase the power of our network. We equipped our ANN with the Levenberg-Marquardt (LM) algorithm as training function to be used and trained with the normalized features computed from the EMG of the left muscles. With the LM algorithm, we were able to achieve the rapid execution of the network.<ref name=":6">Kara S, Dirgenali F, Okkesim S (2006) Detection of gastric dysrhythmia using WT and ANN in diabetic gastroparesis patients. Comput Biol Med 36: 276-290.</ref> | ||
| Line 232: | Line 226: | ||
The features are onset latency, peak-to-peak amplitude, and integral area of the EMG (Ons_lat, Amp, and Int_A, respectively, are used as abbreviations in the following equations). | The features are onset latency, peak-to-peak amplitude, and integral area of the EMG (Ons_lat, Amp, and Int_A, respectively, are used as abbreviations in the following equations). | ||
For proper values to be obtained for the ANN, all column values in Table 1 should be normalized according to Equation 2. Because the features computed from the EMG traces of the left muscles were used as input to the ANN, only normalized features for the left muscles were used. After normalization, all data were regenerated from 0 to 1. <blockquote><math>\tfrac{O_v-Min_v}{Max_v-Min_v}</math> <math>Eq.2</math></blockquote> | For proper values to be obtained for the ANN, all column values in Table 1 should be normalized according to Equation 2. Because the features computed from the EMG traces of the left muscles were used as input to the ANN, only normalized features for the left muscles were used. After normalization, all data were regenerated from 0 to 1. | ||
<blockquote><math>\tfrac{O_v-Min_v}{Max_v-Min_v}</math> <math>Eq.2</math></blockquote>where | |||
<math>O_v=</math> Original value | <math>O_v=</math> Original value | ||
| Line 242: | Line 237: | ||
If values computed from Equation 2 are used as input to the ANN, inferences can be drawn according to the column with the highest correlation. Although the correlation is lower, the other columns show correlation well. If ANN equipped using only the highest correlation, the correlation of the other columns will be ignored. To prevent this kind of guidance, all the row values were normalized according to Equations 3.1, 3.2, and 3.3 for the features computed from the EMG traces of the left muscles, were the subscript ''n'' indicates the normalized value. After the first normalization, there was no unit belonging to a specific feature, and the second normalization procedure could be applied. <blockquote> | If values computed from Equation 2 are used as input to the ANN, inferences can be drawn according to the column with the highest correlation. Although the correlation is lower, the other columns show correlation well. If ANN equipped using only the highest correlation, the correlation of the other columns will be ignored. To prevent this kind of guidance, all the row values were normalized according to Equations 3.1, 3.2, and 3.3 for the features computed from the EMG traces of the left muscles, were the subscript ''n'' indicates the normalized value. After the first normalization, there was no unit belonging to a specific feature, and the second normalization procedure could be applied. <blockquote> | ||
<math>Ons-lat_n= \tfrac{Ons-lat}{\sqrt{ Ons-lat^2+Amp^2+Int-A^2}}</math> | |||
<math>Eq.3.1</math></blockquote><blockquote><math>Ons-lat_n= \tfrac{Amp}{\sqrt{ Ons-lat^2+Amp^2+Int-A^2}}</math> | |||
<math>Eq. 3.2</math></blockquote><blockquote><math>Ons-lat_n= \tfrac{Int-lat}{\sqrt{ Ons-lat^2+Amp^2+Int-A^2}}</math> | |||
<math>Eq.3.3</math></blockquote>The correlation coefficients (CC) were computed based on raw EMG values in Equations 4.1, 4.2 and 4.3, to obtain characteristics of the ANN output. | |||
<blockquote> | |||
<math>CC-Onset-Latency=\tfrac{Right-Onset-Latency}{Left-Onset-Latency}</math> | |||
<math>Eq.4.1</math></blockquote><blockquote><math>CC-Amplitude=\tfrac{Right-Amplitude}{Left-Amplitude}</math> | |||
<math>Eq.4.2</math></blockquote><blockquote><math>CC-Integrated-Area=\tfrac{Right-Integrated -Area}{Left-Integrated -Area}</math> | |||
<math>Eq.4.3</math></blockquote> | |||
Therefore we first defined the characteristics of the network, defined the appropriate input and desired output (called target into the ANN) of the network. Then we adopted the LM algorithm to train the network as described above. But we used the ANN to test the correlation between the EMG values of the right and left muscles. | |||
<math> | When the training was completed, we wanted to check and analyze Neural Network Performance. At this aim, we used the mean squared error (MSE) and the coefficient of determination (<math>R^2</math>). The MSE is the most common measurement for evaluation of the dissimilarity between the outcomes of a model such as the ANN and true values. If the MSE value is small, it means that the model can estimate the true value with almost zero errors. The MSE value was computed according to Equation 5: | ||
<blockquote> | |||
<math>MSE=\tfrac{1}{N}\sum_{i=1}^N(CC_{i,e}-CC_{i,t})^2</math> | |||
<math>Eq. 5</math> | |||
</blockquote> | |||
Where, <math>CC_{i,e}</math> is the ''i''th estimated value and <math>CC_{i,t}</math> is the ''<math>i^{th}</math>'' true value. For a more reliable test evaluating the model’s success, the R2 was added as a statistical measure. The most important reason for computing <math>R^2</math> is to obtain a measure of how well upcoming outcomes are likely to be estimated by the model. The <math>R^2</math> value is an indication of the relationship between the outputs and targets. If <math>R^2=1</math>, this indicates that there is an exact linear relationship between ANN outputs and targets. If <math>R^2</math> is close to zero, then there is no linear relationship between outputs and targets. The <math>R^2</math> value was computed according to Equation 6: | Where, <math>CC_{i,e}</math> is the ''i''th estimated value and <math>CC_{i,t}</math> is the ''<math>i^{th}</math>'' true value. For a more reliable test evaluating the model’s success, the R2 was added as a statistical measure. The most important reason for computing <math>R^2</math> is to obtain a measure of how well upcoming outcomes are likely to be estimated by the model. The <math>R^2</math> value is an indication of the relationship between the outputs and targets. If <math>R^2=1</math>, this indicates that there is an exact linear relationship between ANN outputs and targets. If <math>R^2</math> is close to zero, then there is no linear relationship between outputs and targets. The <math>R^2</math> value was computed according to Equation 6: | ||
<blockquote> | |||
<math>MSE=\tfrac{\sum_{i=1}^N(CC_{i,e}-CC_{i,t})^2}{\sum_{i=1}^N(CC_{i,e}-\bar{CC}_{e})^2}</math> | |||
<math>Eq. 6</math> | |||
</blockquote> | |||
Where, <math>CC_{i,e}</math> is the ''i''th estimated value, <math>CC_{i,t}</math> is the ''<math>i^{th}</math>'' true value, and ''<math>\bar{CC}_{e}</math>'' is the mean of the estimated values.<br /> | Where, <math>CC_{i,e}</math> is the ''i''th estimated value, <math>CC_{i,t}</math> is the ''<math>i^{th}</math>'' true value, and ''<math>\bar{CC}_{e}</math>'' is the mean of the estimated values.<br /> | ||
==Results== | ==Results== | ||
The table 1 | The table 1 shows the list of row EMG value which were subsequently normalized and weighed in order to train – as input – the ANN. In Table 2 we report instead the descriptive and comparative statistical results. | ||
Standardized asymmetry (*) and Standardized Kurtosis (**) outside -2 to +2 range indicate significant deviations from normality and could compromise the validity of many | With regard to the descriptive statistical aspect we can consider the mean and SD values for onset latency (1.96 msec ± 0.18 msec vs. 2.01 msec ± 0.21 msec), amplitude (5.76 mV ± 2.01 mV vs''.'' 5.89 mV ± 2.51 mV) and integral area (11.09 mV/msec ± 4.45 mV/msec vs''.'' 11.27 mV/msec ± 4.34 mV/msec) for right and left masseter, respectively. | ||
[[File:Symmetry 2.jpg|thumb|'''Table 2:''' <br /> | |||
The table shows statistically descriptive data and ''p''-values between sides for onset latency, amplitude and integral area of the bR-MEPs.<br /> | |||
Standardized asymmetry (*) and Standardized Kurtosis (**) outside -2 to +2 range indicate significant deviations from normality and could compromise the validity of many statistical procedures.|alt=|500px]] | |||
The Kruskal-Wallis test shows a statistically not significant difference between the medians (confidence level 95%); in fact, we obtained <math>p-value</math> as 0.33, 0.96 and 0.86 between sides for latency, amplitude and the EMG integral area, respectively for the <sub>b</sub>R-MEPs (Table 2). | |||
In this study, ANN is used to predict the values of the right side by inputting values from the left side. Then the left- and right-side values are combined in a ratio called | In this study, ANN is used to predict the values of the right side by inputting values from the left side. Then the left- and right-side values are combined in a ratio called 'correlation coefficient'. Then the correlation coefficient is computed for the actual observed values (right/left) and then, additionally, for the ratio of the ANN-derived right/left. | ||
The MSE and the <math>R^2</math> were computed to test the ANN. If the ANN estimated the correlation coefficients with zero error, MSE must be 0 and the <math>R^2</math> must be 1. In comparison of the correlation coefficients which computed from the EMG signals of the right and the left muscles and the outcomes of the ANN (Table 3) which were trained with the normalized features computed from the EMG of the left muscles, it can be seen that the outcomes of the ANN are closest to the correlation coefficients (Table 4), and that ANN is able to compute correlation coefficients, based on features of only the left muscles, with almost zero errors. | The MSE and the <math>R^2</math> were computed to test the ANN. If the ANN estimated the correlation coefficients with zero error, MSE must be 0 and the <math>R^2</math> must be 1. In comparison of the correlation coefficients which computed from the EMG signals of the right and the left muscles and the outcomes of the ANN (Table 3) which were trained with the normalized features computed from the EMG of the left muscles, it can be seen that the outcomes of the ANN are closest to the correlation coefficients (Table 4), and that ANN is able to compute correlation coefficients, based on features of only the left muscles, with almost zero errors. | ||
[[File:Senza nomeSymmetry 3a.jpg|left|thumb|'''Table 3:''' This table shows the correlation coefficients, which can be computed with Equations 3.1, 3.2, and 3.3, and the correlation coefficients computed by ANN.]] | [[File:Senza nomeSymmetry 3a.jpg|left|thumb|'''Table 3:''' This table shows the correlation coefficients, which can be computed with Equations 3.1, 3.2, and 3.3, and the correlation coefficients computed by ANN.]] | ||
Therefore, we can conclude that there is an organic symmetry between the left and right sides of the trigeminal motor system. | |||
Therefore, | |||
Figure 2 shows the neuromuscular responses of patient #20 (Table 1) with the measurements of latency (+), peak-to-peak amplitude (*), and integral area (x). The high symmetry of the <sub>b</sub>R-MEPs can be observed.<br /> | Figure 2 shows the neuromuscular responses of patient #20 (Table 1) with the measurements of latency (+), peak-to-peak amplitude (*), and integral area (x). The high symmetry of the <sub>b</sub>R-MEPs can be observed.<br /> | ||
[[File:Symmetry 3.jpg|left|thumb|'''Table 4:''' This table shows the MSE and R2 values, which were computed to test the output of the ANN. MSE values, are very close to zero, and R2 values are very close to 1: our ANN is well able build up a good model starting from our inputs.]] | [[File:Symmetry 3.jpg|left|thumb|'''Table 4:''' This table shows the MSE and R2 values, which were computed to test the output of the ANN. MSE values, are very close to zero, and R2 values are very close to 1: our ANN is well able build up a good model starting from our inputs.]] | ||
The close correspondence between the values calculated by ANN for right masseter starting from the left masseter is irrefutable index of organic symmetry of the trigeminal motor system. | The close correspondence between the values calculated by ANN for right masseter starting from the left masseter is an irrefutable index of organic symmetry of the trigeminal motor system. | ||
The similarity between sides of the data sampled of the <sub>b</sub>R-MEPs (<math>p-value>0.05</math>), the tendency to 0-value for the mean squared error (MSE=0.032, 0.162, 0.212) and the trend to 1-value for the coefficient of determination (<math>R^2= 0.955,0,948,0,947</math>) for the latency, amplitude and integral area respectively, confirm the high efficiency in terms of the symmetry and stability of the <sub>b</sub>R-MEPs as a normalization factor. | The similarity between the sides of the data sampled of the <sub>b</sub>R-MEPs (<math>p-value>0.05</math>), the tendency to 0-value for the mean squared error (MSE=0.032, 0.162, 0.212) and the trend to 1-value for the coefficient of determination (<math>R^2= 0.955,0,948,0,947</math>) for the latency, amplitude and integral area respectively, confirm the high efficiency in terms of the symmetry and stability of the <sub>b</sub>R-MEPs as a normalization factor. | ||
This normalization model implies to a series of requirements such as the stability of the neuromuscular responses, the assessment of | This normalization model implies to a series of requirements such as the stability of the neuromuscular responses, the assessment of | ||
“ <math>_mANEE</math> ” and the symmetry between sides of this last parameter. | “<math>_mANEE</math> ” and the symmetry between sides of this last parameter. | ||
==Discussion== | ==Discussion== | ||
As we have seen above, our results show that, for the normalization factor, we have tested at least three characteristics: the maximal absolute value of the neural evoked energy (<math>_mANEE</math>), the stability and synchronicity of the neuromuscular responses. The electrophysiological symmetry between sides basically indicates an organic symmetry of the motor of the trigeminal nervous system. | As we have seen above, our results show that, for the normalization factor, we have tested at least three characteristics: | ||
#the maximal absolute value of the neural evoked energy (<math>_mANEE</math>), | |||
#the stability of the neuromuscular responses and | |||
#the synchronicity of the neuromuscular responses. | |||
The electrophysiological symmetry between the sides basically indicates an organic symmetry of the motor of the trigeminal nervous system. | |||
The following discussion will focus first on the concept and models of normalization factors, second on the discussion regarding the stability of the <math>_mANEE</math> and third on the organic symmetry of the <sub>b</sub>R- MEPs. | The following discussion will focus first on the concept and models of normalization factors, second on the discussion regarding the stability of the <math>_mANEE</math>, and third on the organic symmetry of the <sub>b</sub>R- MEPs. | ||
===EMG normalization=== | ===EMG normalization=== | ||
Normalization is computed by dividing the EMG from a specific task or event by the EMG from a reference contraction of the same muscle.<ref name=":0">Clarys JP, Cabri J (1993) Electromyography and the study of sports movements: a review. J Sports Sci 11: 379-448.</ref> Additionally, in healthy individuals, normalizing EMGs by using the EMG recorded from a maximal voluntary contraction (MVC), as the reference value may allow the electromyographer to assess what percentage of the maximal activation capacity of the muscle is represented by the EMG task.<ref>Allison GT, Godfrey P, Robinson G (1998) EMG signal amplitude assessment during abdominal bracing and hollowing. J Electromyogr Kinesiol 8: 51-57.</ref> | Normalization is computed by dividing the EMG from a specific task or event by the EMG from a reference contraction of the same muscle.<ref name=":0">Clarys JP, Cabri J (1993) Electromyography and the study of sports movements: a review. J Sports Sci 11: 379-448.</ref> Additionally, in healthy individuals, normalizing EMGs by using the EMG recorded from a maximal voluntary contraction (MVC), as the reference value may allow the electromyographer to assess what percentage of the maximal activation capacity of the muscle is represented by the EMG task.<ref>Allison GT, Godfrey P, Robinson G (1998) EMG signal amplitude assessment during abdominal bracing and hollowing. J Electromyogr Kinesiol 8: 51-57.</ref> | ||
One first criticism could be that this method yields outputs that are in excess of unity or one hundred percent<ref name=":0" /> particularly during rapid and forceful contractions or muscle lengthening. For this reason, Yang<ref>Yang JF, Winter DA (1984) Electromyographic amplitude normalization methods: improving their sensitivity as diagnostic tools in gait analysis. Arch Phys Med Rehabil 65: 517-521.</ref> | One first criticism could be that this method yields outputs that are in excess of unity or one hundred percent<ref name=":0" /> particularly during rapid and forceful contractions or muscle lengthening. For this reason, Yang advocated the use of EMGs arising from contractions which are less than 80% of MVC in order to provide a more stable reference value.<ref>Yang JF, Winter DA (1984) Electromyographic amplitude normalization methods: improving their sensitivity as diagnostic tools in gait analysis. Arch Phys Med Rehabil 65: 517-521.</ref> | ||
To avoid the MVC limitations described above, another EMG model has been proposed as normalization factor. | To avoid the MVC limitations described above, another EMG model has been proposed as normalization factor. | ||
In a recent article,<ref>Calder KM, Hall LA, Lester SM, Inglis JG, Gabriel DA (2005) [https://pubmed.ncbi.nlm.nih.gov/16332261/ Reliability of the biceps brachii M-wave.] J Neuroeng Rehabil 2: 33.</ref> | In a recent article, the authors confirmed that the results of their study support the use of P-P amplitude of the maximum <math>H-wave</math> as a methodological control in <math>H-wave</math> studies and as a normalization factor for voluntary EMG.<ref>Calder KM, Hall LA, Lester SM, Inglis JG, Gabriel DA (2005) [https://pubmed.ncbi.nlm.nih.gov/16332261/ Reliability of the biceps brachii M-wave.] J Neuroeng Rehabil 2: 33.</ref> | ||
Regarding the masticatory system we can evoke both an <math>H-wave</math> and a <math>T-wave</math>, also called jaw-stretch reflex. | Regarding the masticatory system we can evoke both an <math>H-wave</math> and a <math>T-wave</math>, also called 'jaw-stretch reflex'. | ||
The jaw-stretch reflex is the short-latency excitatory response in the jaw-closing muscles after the application of a sudden stretch. It is considered the trigeminal equivalent of the monosynaptic spinal stretch reflex in limb muscles.<ref>Lund JP, Lamarre Y, Lavigne G, Duquet G (1983) Human jaw reflexes. Adv Neurol 39: 739-755.</ref> The simplest way to provoke a jaw stretch reflex is by tapping the chin with a reflex hammer.<ref>Murray GM, Klineberg IJ (1984) A standardized system for evoking reflexes in human jaw elevator muscles. J Oral Rehabil 11: 361-372.</ref><ref>Cruccu G, Frisardi G, van Steenberghe D (1992) Side asymmetry of the jaw jerk in human craniomandibular dysfunction. Arch Oral Biol 37: 257-262.</ref> | The jaw-stretch reflex is the short-latency excitatory response in the jaw-closing muscles after the application of a sudden stretch. It is considered the trigeminal equivalent of the monosynaptic spinal stretch reflex in limb muscles.<ref>Lund JP, Lamarre Y, Lavigne G, Duquet G (1983) Human jaw reflexes. Adv Neurol 39: 739-755.</ref> The simplest way to provoke a jaw stretch reflex is by tapping the chin with a reflex hammer.<ref>Murray GM, Klineberg IJ (1984) A standardized system for evoking reflexes in human jaw elevator muscles. J Oral Rehabil 11: 361-372.</ref><ref>Cruccu G, Frisardi G, van Steenberghe D (1992) Side asymmetry of the jaw jerk in human craniomandibular dysfunction. Arch Oral Biol 37: 257-262.</ref> | ||
| Line 319: | Line 329: | ||
Some authors have tried to test the hypothesis that normalization of the jaw-stretch reflex amplitude with respect to the voluntary EMG activity preceding the reflex stimulus (EMG pre-stimulus) makes the amplitude more independent by the electrode location over the masseter muscle. In this experimental study, the reflex amplitude was also normalized with respect to the mean pre-stimulus EMG activity.<ref>Koutris M, Naeije M, Lobbezoo F, Wang K, Arendt-Nielsen L, et al. (2010) Normalization reduces the spatial dependency of the jaw-stretch reflex activity in the human masseter muscle. Muscle Nerve 41: 78-84.</ref> | Some authors have tried to test the hypothesis that normalization of the jaw-stretch reflex amplitude with respect to the voluntary EMG activity preceding the reflex stimulus (EMG pre-stimulus) makes the amplitude more independent by the electrode location over the masseter muscle. In this experimental study, the reflex amplitude was also normalized with respect to the mean pre-stimulus EMG activity.<ref>Koutris M, Naeije M, Lobbezoo F, Wang K, Arendt-Nielsen L, et al. (2010) Normalization reduces the spatial dependency of the jaw-stretch reflex activity in the human masseter muscle. Muscle Nerve 41: 78-84.</ref> | ||
Unfortunately, the proposed model gave us few neurophysiological indications being the P-P amplitude of the jaw in excess, respect to unity or 100% as aforementioned <ref name=":0" /> | Unfortunately, the proposed model gave us few neurophysiological indications being the P-P amplitude of the jaw in excess, respect to unity or 100% as aforementioned <ref name=":0" />. Why not use the masseteric <math>M-wave</math> as a normalization factor, higher in amplitude and more stable than the MVC?<ref name=":1">Arabadzhiev TI, Dimitrov VG, Dimitrova NA, Dimitrov GV (2010) Interpretation of EMG integral or RMS and estimates of “neuromuscular efficiency” can be misleading in fatiguing contraction. J Electromyogr Kinesiol 20: 223-232.</ref> | ||
The technical execution of <math>M-wave</math> for the trigeminal nervous system is much more painful and invasive than that of the spinal cord. To evoke a direct response from the masseter muscle, in fact, it is necessary to insert an insulated in-tip needle electrode about 2 cm deep in the temporal fossa and this makes the technique not clinically applicable, although it could obtain more detailed information for the neurophysiological interpretation data. | The technical execution of <math>M-wave</math> for the trigeminal nervous system is much more painful and invasive than that of the spinal cord. To evoke a direct response from the masseter muscle, in fact, it is necessary to insert an insulated in-tip needle electrode about 2 cm deep in the temporal fossa and this makes the technique not clinically applicable, although it could obtain more detailed information for the neurophysiological interpretation data. | ||
===<sub>maximal</sub>Absolute Neural Evoked Energy <math>_mANEE</math>=== | ===<sub>maximal</sub>Absolute Neural Evoked Energy <math>_mANEE</math>=== | ||
[[File:Potenziale Evocato della Radice Trigeminale.jpg|left|thumb|'''Figure 3:''' The figure shows the signal saturation of the root with respect to latency and amplitude.]] | [[File:Potenziale Evocato della Radice Trigeminale.jpg|left|thumb|'''Figure 3:''' The figure shows the signal saturation of the root with respect to latency and amplitude.]] | ||
like in the most recent Wavelet algorithm,<ref>Bonato P, Roy SH, Knaflitz M, De Luca CJ (2001) Time-frequency parameters of the surface myoelectric signal for assessing muscle fatigue during cyclic dynamic contractions. IEEE Trans Biomed Eng 48: 745-753.</ref> but it still remains very difficult, if not impossible in some cases, to separate the EMG signal from the unavoidable noise. | As already mentioned, the electromyographic signals show high complexity, and the mechanisms underlying the generation of EMG signals appear to be non-linear or even chaotic in nature. Researchers are trying, however, to improve the systems of mathematical filtering like in the most recent Wavelet algorithm,<ref>Bonato P, Roy SH, Knaflitz M, De Luca CJ (2001) Time-frequency parameters of the surface myoelectric signal for assessing muscle fatigue during cyclic dynamic contractions. IEEE Trans Biomed Eng 48: 745-753.</ref>, but it still remains very difficult, if not impossible in some cases, to separate the EMG signal from the unavoidable noise. | ||
In this model of normalization, the purpose is not the decomposition of the signal/noise ratio, that we prefer to consider as an entropic phenomenon,<ref>Xie HB, Guo JY, Zheng YP (2010) Fuzzy approximate entropy analysis of chaotic and natural complex systems: detecting muscle fatigue using electromyography signals. Ann Biomed Eng 38: 1483-1496.</ref> but to decouple the contents of the central drive <ref>Inghilleri M, Berardelli A, Cruccu G, Priori A, Manfredi M (1989) Corticospinal potentials after transcranial stimulation in humans. J Neurol Neurosurg Psychiatry 52: 970-974.</ref> from the peripheral drive<ref>Cruccu G, Iannetti GD, Marx JJ, Thoemke F, Truini A, et al. (2005) Brainstem reflex circuits revisited. Brain 128: 386-394.</ref><ref>Kennelly KD (2012) Electrodiagnostic approach to cranial neuropathies. Neurol Clin 30: 661-684.</ref>by normalizing them with the organic content extrapolated from the <sub>b</sub>R-MEPs. | In this model of normalization, the purpose is not the decomposition of the signal/noise ratio, that we prefer to consider as an entropic phenomenon,<ref>Xie HB, Guo JY, Zheng YP (2010) Fuzzy approximate entropy analysis of chaotic and natural complex systems: detecting muscle fatigue using electromyography signals. Ann Biomed Eng 38: 1483-1496.</ref> but to decouple the contents of the central drive <ref>Inghilleri M, Berardelli A, Cruccu G, Priori A, Manfredi M (1989) Corticospinal potentials after transcranial stimulation in humans. J Neurol Neurosurg Psychiatry 52: 970-974.</ref> from the peripheral drive<ref>Cruccu G, Iannetti GD, Marx JJ, Thoemke F, Truini A, et al. (2005) Brainstem reflex circuits revisited. Brain 128: 386-394.</ref><ref>Kennelly KD (2012) Electrodiagnostic approach to cranial neuropathies. Neurol Clin 30: 661-684.</ref>by normalizing them with the organic content extrapolated from the <sub>b</sub>R-MEPs. | ||
| Line 342: | Line 351: | ||
===<sub>b</sub>R-MEPs stability and synchronicity=== | ===<sub>b</sub>R-MEPs stability and synchronicity=== | ||
[[File:TCS - Motor Evoked Potentials of trigeminal roots in open bite patient.jpg|thumb|'''Figure 2''': Motor evoked potentials elicited by transcranial electrical stimulation of both trigeminal roots]] | [[File:TCS - Motor Evoked Potentials of trigeminal roots in open bite patient.jpg|thumb|'''Figure 2''': Motor evoked potentials elicited by transcranial electrical stimulation of both trigeminal roots]] | ||
Another essential element to support the proposed normalization factor is its stability and synchronicity in the neuromuscular response. | Another essential element to support the proposed normalization factor is its stability and synchronicity in the neuromuscular response. | ||
| Line 351: | Line 359: | ||
We have to add to these biases an even more limiting phenomenon than the intracranial current distribution with vectorial summation and collision current phenomena. However, the morphology of the <sub>b</sub>R-MEPs (Figure 2) and the difference in latency and amplitude (0.04 msec and 400 μV, respectively) reported in Table 2, confirm the high stability and synchronicity of the <sub>b</sub>R-MEPs. Keep in mind that, in order to extract the maximum efficiency from the normalization model proposed, any functional tests, such as trigeminal reflexes, must be performed in the same session and, therefore, with the same electrode arrangement. This way it will significantly reduce distortion due to the recording geometry. | We have to add to these biases an even more limiting phenomenon than the intracranial current distribution with vectorial summation and collision current phenomena. However, the morphology of the <sub>b</sub>R-MEPs (Figure 2) and the difference in latency and amplitude (0.04 msec and 400 μV, respectively) reported in Table 2, confirm the high stability and synchronicity of the <sub>b</sub>R-MEPs. Keep in mind that, in order to extract the maximum efficiency from the normalization model proposed, any functional tests, such as trigeminal reflexes, must be performed in the same session and, therefore, with the same electrode arrangement. This way it will significantly reduce distortion due to the recording geometry. | ||
====Organic symmetry==== | ====Organic symmetry==== | ||
| Line 359: | Line 365: | ||
A reflex opening of the jaw, resulting from the simultaneous relaxation of jaw closers and contraction of jaw openers, not only helps to avoid injuries to the oral tissues, but also could contribute to coordinating rhythmic masticatory movements.<ref>Shigenaga Y, Yoshida A, Mitsuhiro Y, Tsuru K, Doe K (1988) Morphological and functional properties of trigeminal nucleus oralis neurons projecting to the trigeminal motor nucleus of the cat. Brain Res 461: 143-149.</ref>The stimulus applied to one side evokes the reflex bilaterally in a nearly symmetrical fashion. The symmetrical output is characteristic of most of the jaw movements induced by sensory signals both from the peripheral tissue and from those generated by signals coming from the cerebral cortex. | A reflex opening of the jaw, resulting from the simultaneous relaxation of jaw closers and contraction of jaw openers, not only helps to avoid injuries to the oral tissues, but also could contribute to coordinating rhythmic masticatory movements.<ref>Shigenaga Y, Yoshida A, Mitsuhiro Y, Tsuru K, Doe K (1988) Morphological and functional properties of trigeminal nucleus oralis neurons projecting to the trigeminal motor nucleus of the cat. Brain Res 461: 143-149.</ref>The stimulus applied to one side evokes the reflex bilaterally in a nearly symmetrical fashion. The symmetrical output is characteristic of most of the jaw movements induced by sensory signals both from the peripheral tissue and from those generated by signals coming from the cerebral cortex. | ||
Previous studies <ref>Nakamura Y, Nagashima H, Mori S (1973) Bilateral effects of the afferent impulses from the masseteric muscle on the trigeminal motoneuron of the cat. Brain Res 57: 15-27.</ref> | Previous studies have shown that peripheral stimulation evokes inhibitory postsynaptic potentials (IPSPs) in bilateral jaw-closer motor neurons.<ref>Nakamura Y, Nagashima H, Mori S (1973) Bilateral effects of the afferent impulses from the masseteric muscle on the trigeminal motoneuron of the cat. Brain Res 57: 15-27.</ref> This bilateral inhibition is mediated, at least in part, by supra- and juxta-trigeminal neurons with bifurcating axons projecting to both the right and the left masseter motor neurons. The goal of a recent study was to morphologically analyse how the functional symmetry of the masticatory system might be reflected in the organisation of pre-motor neurons and how it could be able to mediate excitation of jaw-opener motor-neurons.<ref>Yoshida A, Yamamoto M, Moritani M, Fukami H, Bae YC, et al. (2005) Bilateral projection of functionally characterized trigeminal oralis neurons to trigeminal motoneurons in cats. Brain Res 1036: 208-212.</ref> | ||
It has been demonstrated that in the masticatory system, where symmetrical motor output is the rule, employing neurons with bifurcating axons as a pre-motor element might be a common strategy for mediation of both peripheral and central signals. | It has been demonstrated that in the masticatory system, where symmetrical motor output is the rule, employing neurons with bifurcating axons as a pre-motor element might be a common strategy for mediation of both peripheral and central signals. | ||
Latest revision as of 13:12, 2 October 2022
In order to achieve a complete clinical evaluation of mastication, an in-depth neurophysiopathological assessment of masticatory muscles control is required. Electromyography technique (EMG) is widely used for this purpose, but failed to provide convincing results.
The aim of this work was to describe our quantitative objectivation of the motor control of the masticatory muscles and to verify the hypothesis to consider the bilateral Root Motor Evoked Potentials as an electrophysiological normalization factor.
Introduction
For a correct evaluation of masticatories functions, a precise knowledge of the forces involved in the action and the resulting movements are required. Although these can be easily and accurately measured with many different kind of instrumentation, the real underlying problem is represented by the masticatory muscles control assessment from a neuro-physiopathological point of view.
(EMG) technique has been extensively used in this domain but there is still a series of concerns regarding the reliability of EMG-based measures for the level of muscles activation’s assessment and even the symmetry and synchrony of muscles’ activation on the two sides [1].
Neither the conventional analysis of Integrated electromyographic activity (IEMG) and the Root Mean Square of EMG of masticatory muscles (RMSEMG), nor the unconventional analysis based upon the trigeminal reflexes, known as the jaw jerk, masseteric inhibitory silent period, masseteric inhibitory recovery cycle etc., can be reliably used for this purpose due to the methodological errors and also because many conditions in health and disease may affect the resulting EMG signal.
That’s why most of the studies performed so far, aimed at showing a possible correlation between EMG signals with Temporomandibular Disorders (TMD), Orofacial Pain (OP) or Incorrect Occlusion (IO), failed to give convincing results[2][3][4][5][6]. It should also be noted that in a very small proportion of OP patients visited by dental specialists, some neurological diseases as intracranial cancers, multiple sclerosis and so on are the underlying symptomatological cause of TMD or OP. These patients, who actually suffer from misunderstood neurological symptoms, may undergo unnecessary dental interventions before the correct diagnosis is made, often too late[7][8].
The EMG signal
EMG signal is the most common method applied to study these patients. However many pathophysiological phenomena and the nature of the signal influence the measure and create an hard barriers against a reliable application of this findings. These errors are compounded by the counterintuitive effects that some system parameters can have on the EMG signal like the phenomenon of crosstalk, amplitude cancellation and the non-stationary of the EMG signal[9].
Although there are many traditional methods as well as innovative methods for EMG’s signal elaboration, a precise correlation between EMG and health condition of the underlying neurological structures is still difficult to obtain.[10]
The EMG is one of the most prominent techniques to describe how the nervous system is controlling the masticatory system. EMG signals acquired on the skin surface may be used to assess the intensity and timing of a voluntary, involuntary or reflex contraction. There are at least two main orders of motivations regarding the reliability of the EMG like bioengineering and anatomic arguments. Regarding to bioengineering argumentation, the quantity of the so- called “Neural Energy” [11][12], namely the total electrical signal sent from the central nervous system to muscle[13] and that now we call maximal Absolute Neural Evoked Energy “ ”, variations in the central command or in the central drive to motoneurons [14][15][16][17] were often estimated by IEMG or RMSEMG or by their changes.
The trigeminal motor system
The second argumentation for the unreliability of EMG lies in the neuroanatomy and neurofunctionality itself of the masticatory system and notably of the trigeminal motor system.
The cortical projections to trigeminal motoneurons are generally believed to be bilateral and symmetric and by means of electrical or magnetic brain stimulation through the intact scalp[18] [19] it is possible to evoke Motor responses in masticatory muscles.
Evoking a response on masticatory muscles by transcranial magnetic stimulation with the coil placed on the vertex of the scalp, it is possible to elicitate a cortical potential called Cortex-MEPs (C-MEPs) relatively symmetrical between sides with a latency of about 6 msec and maximum amplitude which reaches only 30% of the M-wave. In addition, the C-MEPs are evoked only in the presence of facilitation exerted by a voluntary contraction of the subject like ask to clench the teeth moderately in order to facilitate the trigeminal cortical motoneurons. The C-MEPs, therefore, it can be considered as a functional response of the trigeminal nervous system and absolutely not suitable as a normalization factor, because there are too variables modulated by the peripheral and central drive.
In the ipsilateral masseter, the electrical Transcranial Stimulation (eTCS) is able to evoke a large, short-latency potential in the relaxed as well as the active muscles. The features of the ipsilateral MEPs did not change in relaxed or active conditions. The mean onset latency is about 2 ms, peak latency 3.9 ms, and amplitude 5.4 mV and there is no latency variability. For the hemiplegic patients, symmetric ipsilateral MEPs were obtained between sides, identical to those recorded in healthy subjects. These motor potentials, considered secondary to excitation of the trigeminal motor root, were called Root- MEPs (R-MEPs) to differentiate them from M waves and C-MEPs.[20]
The R-MEPs, therefore, could be considered an organic response because not modulated neither by central nor peripheral drive and shows an absolute stability giving important information about the anatomical integrity of the trigeminal motor system.
According to this stability, the R-MEPs may be considered as a normalization organic factor. In this work we studied the muscular evoked potentials on the masseters muscles after the direct bilateral stimulation of the motor roots of the trigeminal motor system called bilateral Root Motor Evoked Potentials (bR-MEPs) by transcranial in the electrical stimulation. The , symmetry and synchrony properties of the resulting bR-MEPs were studied using measures like latency, amplitude and integrated area of the signal. This technique could allow us, from the neurphysiopathological point of view, a better assessment of masticatory function and to verify the possibility to consider the bR- MEPs as a normalization landmark. This technique will implement the already widely used electrophysiological standardized methods, like conventional EMG techniques (IEMG or RMSEMG) and unconventional trigeminal reflexes.
Method
Twenty-five people including 15 males (mean age 30 ± 5 years) and 10 females (mean age 27 ± 4 years) with normal occlusion and no history of OP and TMDs underwent to bR-MEPs of the trigeminal motor system. With the exclusion criteria we used, we decided to include only those subjects that are not entered in the classification RDC/TMD. The RDC/ TMD is a biaxial diagnostic tool composed of a clinical exam based on a detailed physical evaluation of the mouth opening pattern, vertical extension of mandibular movement, noises in the TMJ upon palpation during vertical movement, excursive mandibular movements and noises in the Temporomandibular Joint (TMJ) upon palpation during lateral excursion and protrusion.
The RDC/TMD questionnaire is made up of 31 items addressing general health, oral health, history of facial pain, mouth opening limitation, joint noises, habits, bite, ringing in the ears, health conditions in general, joint problems, headache, current behaviour and social and economic profile.[21]
The study was approved by the Human Research Ethics Committee at the Sassari University. Each participant released and signed an informed consent.
Electrophysiological procedure
As above mentioned, the transcranial electrical stimulation (eTCS) of both trigeminal roots induced a neuromuscular response called “bilateral Root-Motor-Evoked Potential” ( R-MEPs). It was performed by an electromyographic device (Nemus -NGF, EBNeuro, Firenze, Italy).[22][23]
Considering the safety limitations,[24] we computed the energy delivered for each single pulse in our application through this formula: per pulse.
Since 2 stimulators were used, the limits were ten times lower than those stated in the IEC regulation.
The electrodes were then arranged as described below. A common anode to the 2 electrostimulators was placed at the vertex, while a cathode electrode was placed on each side at 12-13 cm along the line joining the vertex to the acoustic meatus in the parietal region. The electrical stimulus consisted of a square wave lasting 250 μsec at a voltage of ≅ 300 V and maximum current of 100 mA.
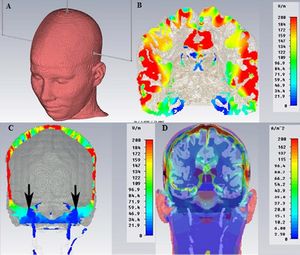
To show the distribution of the electric field inside the intracranial brain tissue we report in Figure 1 an analysis performed through a generic Finite Element process (FE, SimNibs method), only as a descriptive model (data not reported).[25]
Briefly, FE models consisted of around 1.7 million tetrahedra. Mesh resolution was selectively enhanced in Gray Matter (GM), White Matter (WM), skull and the Cerebro Spinal Fluid (CSF) regions with an average tetrahedron volume of . Electrical conductivities were assigned to different tissue types [26] where σskin=0.465 S/m, σskull=0.010 S/m,.[27]
Figure 1 shows the electrode’s arrangement (Figure 1A), the maximum current will spread below the cathodes (in red color) in the parietal cortex (Figure 1B), while in the region of the skull base close to the trigeminal motor root reaches only a small amount of current (Figure 1C, black arrows). Figure 1D shows the current density that spreads below the skull.
We underline how minimal is the amount of electric current inside the brain tissue required to saturate the motor trigeminal root compared to the amount of current need to evoke a response by the trigeminal motor cortex below the cathode and this is one of the reasons that led us to choose this type of evoked response (mainly peripheral) rather than cortical (with higher threshold and less stability in term of neuromuscular response).
We recorded simultaneously the motor-evoked potentials of both the right and left trigeminal roots from the right and left masseter muscles through 2 paired surface electrodes. The EMG device has been set with 20 msec time-window width, with per division and a filter bandwidth of - .
The onset latency, the peak-to-peak amplitude, and the integral area of ten trials of motor-evoked potentials for each side of each subject were analysed and reported as a mean of the ten trials in Table 1.
The onset latency was marked at the first negative deflection of the EMG trace after about 2 msec. The average amplitude corresponded to the positive and negative peak and is calculated in mV, while the measurement of the integral area corresponding to the area below the EMG trace was considered in 3 time divisions (6 msec) from the onset latency and was measured in millivolts per millisecond ().
Statistical analysis
The statistical analysis follows a conventional process aimed at the quantification of the “ ”, which essentially indicates the maximum absolute value delivered by the motor trigeminal nervous system and an unconventional process focused mainly on the symmetry analysis between the sides of the bR-MEPs.
We performed descriptive statistic on the raw EMG values for the computation of mean, standard deviations, analysis of sample’s distribution. The comparison between the two sides for the latencies, amplitudes and EMG integral areas was performed by Kruskal-Wallis test.
Significance was set at a p.
Artificial neural network model
An artificial neural network (ANN) is a general mathematical computing paradigm by which the geometry and functionality of the ANN have been linked to the biological neural system and one of the most interesting characteristic of this paradigm is the self-learning propriety.
The ANN computational model has been used to estimate the correlation coefficient with the EMG values of one side. With the ANNs, we can determine the correlations that describe input/output formulation in a dataset or a system.[28][29]
If organic symmetry exists, there would be a correlation coefficient between the EMG values of the right and left muscles. To test this assumption, we adopted the ANN model. First we created, configured, and initialized our multi-layer ANN.[29]
The multi-layer ANN
We assumed that each layer is composed of a number of predefined neurons.
The neurons in the input layer perform as a buffer which divides into portions and dispense the input signals to the next neurons in the hidden layer without degrading the signal. Each neuron in the hidden layer sums the input signals , after weighting them with the strengths of the respective connections from the input layer, and calculates its output as a function of the sum.
Where, is the weight of the and connection and is the input signal. is the activation function which is needed to transform the weighted sum of all signals influencing a neuron.[28]
In our ANN model, a radial basis function (RBF) has been chosen as the activation function . In the field of mathematical modelling, an artificial neural network that uses RBF as activation function is properly called a 'radial basis function network'. The output of this network is a linear combination of RBF of the inputs and neuron parameters. RBF has many application, and we choose this one because it is specific for function approximation tasks.
Algorithms and network
We decided to initialize two layers and define ten neurons in the hidden layer in order to increase the power of our network. We equipped our ANN with the Levenberg-Marquardt (LM) algorithm as training function to be used and trained with the normalized features computed from the EMG of the left muscles. With the LM algorithm, we were able to achieve the rapid execution of the network.[29]
The back-propagation method was used in the algorithm, which uses a training procedure to adjust the connection weights of a multi-layer ANN. Mainly, the LM algorithm can be described as a least-squares estimation algorithm.
The features are onset latency, peak-to-peak amplitude, and integral area of the EMG (Ons_lat, Amp, and Int_A, respectively, are used as abbreviations in the following equations).
For proper values to be obtained for the ANN, all column values in Table 1 should be normalized according to Equation 2. Because the features computed from the EMG traces of the left muscles were used as input to the ANN, only normalized features for the left muscles were used. After normalization, all data were regenerated from 0 to 1.
where
Original value
Minimum valure in the column
Maximum valure in the column
If values computed from Equation 2 are used as input to the ANN, inferences can be drawn according to the column with the highest correlation. Although the correlation is lower, the other columns show correlation well. If ANN equipped using only the highest correlation, the correlation of the other columns will be ignored. To prevent this kind of guidance, all the row values were normalized according to Equations 3.1, 3.2, and 3.3 for the features computed from the EMG traces of the left muscles, were the subscript n indicates the normalized value. After the first normalization, there was no unit belonging to a specific feature, and the second normalization procedure could be applied.
The correlation coefficients (CC) were computed based on raw EMG values in Equations 4.1, 4.2 and 4.3, to obtain characteristics of the ANN output.
Therefore we first defined the characteristics of the network, defined the appropriate input and desired output (called target into the ANN) of the network. Then we adopted the LM algorithm to train the network as described above. But we used the ANN to test the correlation between the EMG values of the right and left muscles.
When the training was completed, we wanted to check and analyze Neural Network Performance. At this aim, we used the mean squared error (MSE) and the coefficient of determination (). The MSE is the most common measurement for evaluation of the dissimilarity between the outcomes of a model such as the ANN and true values. If the MSE value is small, it means that the model can estimate the true value with almost zero errors. The MSE value was computed according to Equation 5:
Where, is the ith estimated value and is the true value. For a more reliable test evaluating the model’s success, the R2 was added as a statistical measure. The most important reason for computing is to obtain a measure of how well upcoming outcomes are likely to be estimated by the model. The value is an indication of the relationship between the outputs and targets. If , this indicates that there is an exact linear relationship between ANN outputs and targets. If is close to zero, then there is no linear relationship between outputs and targets. The value was computed according to Equation 6:
Where, is the ith estimated value, is the true value, and is the mean of the estimated values.
Results
The table 1 shows the list of row EMG value which were subsequently normalized and weighed in order to train – as input – the ANN. In Table 2 we report instead the descriptive and comparative statistical results.
With regard to the descriptive statistical aspect we can consider the mean and SD values for onset latency (1.96 msec ± 0.18 msec vs. 2.01 msec ± 0.21 msec), amplitude (5.76 mV ± 2.01 mV vs. 5.89 mV ± 2.51 mV) and integral area (11.09 mV/msec ± 4.45 mV/msec vs. 11.27 mV/msec ± 4.34 mV/msec) for right and left masseter, respectively.
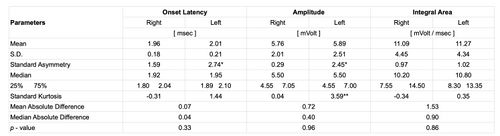
The table shows statistically descriptive data and p-values between sides for onset latency, amplitude and integral area of the bR-MEPs.
Standardized asymmetry (*) and Standardized Kurtosis (**) outside -2 to +2 range indicate significant deviations from normality and could compromise the validity of many statistical procedures.
The Kruskal-Wallis test shows a statistically not significant difference between the medians (confidence level 95%); in fact, we obtained as 0.33, 0.96 and 0.86 between sides for latency, amplitude and the EMG integral area, respectively for the bR-MEPs (Table 2).
In this study, ANN is used to predict the values of the right side by inputting values from the left side. Then the left- and right-side values are combined in a ratio called 'correlation coefficient'. Then the correlation coefficient is computed for the actual observed values (right/left) and then, additionally, for the ratio of the ANN-derived right/left.
The MSE and the were computed to test the ANN. If the ANN estimated the correlation coefficients with zero error, MSE must be 0 and the must be 1. In comparison of the correlation coefficients which computed from the EMG signals of the right and the left muscles and the outcomes of the ANN (Table 3) which were trained with the normalized features computed from the EMG of the left muscles, it can be seen that the outcomes of the ANN are closest to the correlation coefficients (Table 4), and that ANN is able to compute correlation coefficients, based on features of only the left muscles, with almost zero errors.
Therefore, we can conclude that there is an organic symmetry between the left and right sides of the trigeminal motor system.
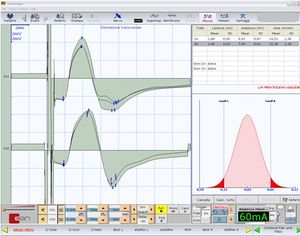
Figure 2 shows the neuromuscular responses of patient #20 (Table 1) with the measurements of latency (+), peak-to-peak amplitude (*), and integral area (x). The high symmetry of the bR-MEPs can be observed.
The close correspondence between the values calculated by ANN for right masseter starting from the left masseter is an irrefutable index of organic symmetry of the trigeminal motor system.
The similarity between the sides of the data sampled of the bR-MEPs (), the tendency to 0-value for the mean squared error (MSE=0.032, 0.162, 0.212) and the trend to 1-value for the coefficient of determination () for the latency, amplitude and integral area respectively, confirm the high efficiency in terms of the symmetry and stability of the bR-MEPs as a normalization factor.
This normalization model implies to a series of requirements such as the stability of the neuromuscular responses, the assessment of
“ ” and the symmetry between sides of this last parameter.
Discussion
As we have seen above, our results show that, for the normalization factor, we have tested at least three characteristics:
- the maximal absolute value of the neural evoked energy (),
- the stability of the neuromuscular responses and
- the synchronicity of the neuromuscular responses.
The electrophysiological symmetry between the sides basically indicates an organic symmetry of the motor of the trigeminal nervous system.
The following discussion will focus first on the concept and models of normalization factors, second on the discussion regarding the stability of the , and third on the organic symmetry of the bR- MEPs.
EMG normalization
Normalization is computed by dividing the EMG from a specific task or event by the EMG from a reference contraction of the same muscle.[30] Additionally, in healthy individuals, normalizing EMGs by using the EMG recorded from a maximal voluntary contraction (MVC), as the reference value may allow the electromyographer to assess what percentage of the maximal activation capacity of the muscle is represented by the EMG task.[31]
One first criticism could be that this method yields outputs that are in excess of unity or one hundred percent[30] particularly during rapid and forceful contractions or muscle lengthening. For this reason, Yang advocated the use of EMGs arising from contractions which are less than 80% of MVC in order to provide a more stable reference value.[32]
To avoid the MVC limitations described above, another EMG model has been proposed as normalization factor.
In a recent article, the authors confirmed that the results of their study support the use of P-P amplitude of the maximum as a methodological control in studies and as a normalization factor for voluntary EMG.[33]
Regarding the masticatory system we can evoke both an and a , also called 'jaw-stretch reflex'.
The jaw-stretch reflex is the short-latency excitatory response in the jaw-closing muscles after the application of a sudden stretch. It is considered the trigeminal equivalent of the monosynaptic spinal stretch reflex in limb muscles.[34] The simplest way to provoke a jaw stretch reflex is by tapping the chin with a reflex hammer.[35][36]
Some authors have tried to test the hypothesis that normalization of the jaw-stretch reflex amplitude with respect to the voluntary EMG activity preceding the reflex stimulus (EMG pre-stimulus) makes the amplitude more independent by the electrode location over the masseter muscle. In this experimental study, the reflex amplitude was also normalized with respect to the mean pre-stimulus EMG activity.[37]
Unfortunately, the proposed model gave us few neurophysiological indications being the P-P amplitude of the jaw in excess, respect to unity or 100% as aforementioned [30]. Why not use the masseteric as a normalization factor, higher in amplitude and more stable than the MVC?[38]
The technical execution of for the trigeminal nervous system is much more painful and invasive than that of the spinal cord. To evoke a direct response from the masseter muscle, in fact, it is necessary to insert an insulated in-tip needle electrode about 2 cm deep in the temporal fossa and this makes the technique not clinically applicable, although it could obtain more detailed information for the neurophysiological interpretation data.
maximalAbsolute Neural Evoked Energy
As already mentioned, the electromyographic signals show high complexity, and the mechanisms underlying the generation of EMG signals appear to be non-linear or even chaotic in nature. Researchers are trying, however, to improve the systems of mathematical filtering like in the most recent Wavelet algorithm,[39], but it still remains very difficult, if not impossible in some cases, to separate the EMG signal from the unavoidable noise.
In this model of normalization, the purpose is not the decomposition of the signal/noise ratio, that we prefer to consider as an entropic phenomenon,[40] but to decouple the contents of the central drive [41] from the peripheral drive[42][43]by normalizing them with the organic content extrapolated from the bR-MEPs.
For this reason, first of all we prefer a phasic signal (R-MEPs) to an asynchronous signal (interference EMG pattern) as the MVC.
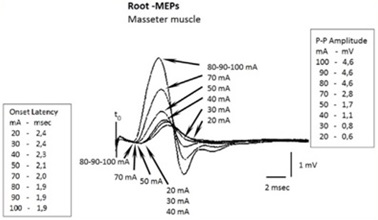
Hence the first procedure is to check for the saturation of the motor trigeminal fiber response. At 20 mA, 30 mA and 40 mA we can see a recorded onset latency of 2.4 msec, 2.4 msec and 2.3 msec respectively and even increasing the amperage we can observe a decrease in latency up to 2.1 msec to 50 mA, 2 msec to 70 mA and 1.9 msec to 80 mA, 90 mA and 100 mA (Figure 3).
These differences in latency up to the maximal current density depend on the capacitive components of the tissues encountered by the intracranial current flow[25][26][27]. The signal saturation of the root is the first step to be performed, even before clinically interpreting a delay in latency.[44][45][46][47]
The saturation of the root with respect to amplitude gives the same results. In fact, at delivered amperage of 80 mA, 90 mA and 100 mA, the P-P amplitude remains at 4.6 mV (Figure 3).
The amplitude value of 4.6 mV (of course the amplitude can be chosen to be equivalent to the integral area, depending on the purpose of the study) and the onset latency of 1.9 msec would correspond to the maximum absolute values of neural energy elicited by the motor of the trigeminal nervous system already called “ ”.
bR-MEPs stability and synchronicity
Another essential element to support the proposed normalization factor is its stability and synchronicity in the neuromuscular response.
The Root-MEPs behave in the same way as the in terms of stability, conceptually differing only in the technical procedures and the site of stimulation in addition to the clinical indications more favourable for the bR-MEPs.
Even the Root-MEPs could change under some conditions including post-tetanic potentiation, release from ischemia and so on.[38] Conditions that, substantially, are due to a peripheral phenomenon inducing changes in the amplitudes of the Compound Motor Action Potential underlying the changes in the profile of intracellular action potential (IAP).
We have to add to these biases an even more limiting phenomenon than the intracranial current distribution with vectorial summation and collision current phenomena. However, the morphology of the bR-MEPs (Figure 2) and the difference in latency and amplitude (0.04 msec and 400 μV, respectively) reported in Table 2, confirm the high stability and synchronicity of the bR-MEPs. Keep in mind that, in order to extract the maximum efficiency from the normalization model proposed, any functional tests, such as trigeminal reflexes, must be performed in the same session and, therefore, with the same electrode arrangement. This way it will significantly reduce distortion due to the recording geometry.
Organic symmetry
To share the concept of organic symmetry of the trigeminal motor system, it is necessary to address some fundamental points about the masticatory system functionality according to the experimental animal studies as well.
A reflex opening of the jaw, resulting from the simultaneous relaxation of jaw closers and contraction of jaw openers, not only helps to avoid injuries to the oral tissues, but also could contribute to coordinating rhythmic masticatory movements.[48]The stimulus applied to one side evokes the reflex bilaterally in a nearly symmetrical fashion. The symmetrical output is characteristic of most of the jaw movements induced by sensory signals both from the peripheral tissue and from those generated by signals coming from the cerebral cortex.
Previous studies have shown that peripheral stimulation evokes inhibitory postsynaptic potentials (IPSPs) in bilateral jaw-closer motor neurons.[49] This bilateral inhibition is mediated, at least in part, by supra- and juxta-trigeminal neurons with bifurcating axons projecting to both the right and the left masseter motor neurons. The goal of a recent study was to morphologically analyse how the functional symmetry of the masticatory system might be reflected in the organisation of pre-motor neurons and how it could be able to mediate excitation of jaw-opener motor-neurons.[50]
It has been demonstrated that in the masticatory system, where symmetrical motor output is the rule, employing neurons with bifurcating axons as a pre-motor element might be a common strategy for mediation of both peripheral and central signals.
The concept of organic symmetry is not restricted solely to the masticatory system but can be found in complex neuronal processes in which the output is the result of the sensorimotor drive of the central and peripheral nervous systems.
The vestibular system is a sensorimotor system where a sophisticated phenomenon of symmetry can be found. Recently, spatially related symmetry groups were viewed as anatomical and physiological organisers of the central vestibular system (CVS)[51] and according to this concept, the author has demonstrated that there are discrete rotational symmetries in the neck-canal pathway and in the canal pathway to the uvula-nodulus. Since the sensory receptors, neuronal pathways and muscles are discrete, these discrete rotations can be considered the skeleton of the nervous system for Noether symmetries.[52]
The H-wave is certainly the most reliable index used in clinical practice and randomised drug trials. It is obtained by direct stimulation of the afferent fibre of the nerve trunk, short-circuiting the muscle spindle so as to obtain a reflex response similar to that evoked by a physiologically stretched tendon. In an interesting study, analysis of the data obtained by the simultaneous stimulation of both legs showed a high degree of symmetry of the spinal reflex circuits.[53]
The neuromuscular responses of the masseter to a strong acoustic stimulation have also been described as two bilateral and symmetrical short-latency waves: the first at high threshold ( and ) of saccular origin and the second ( and ) of cochlear origin. It is interesting to note the high level of symmetry between the sides.[54]
Conclusions
The present study shows that synchronicity, symmetry, and the maximum value of the neural energy evoked are essential parameters in order to consider the bR-MEPS a reliable organic normalization factor. The amplitude of the muscular potential in combination with the high symmetry can provide indications about the trigeminal nervous system integrity. It could be employed in odontology disciplines and in the field of orofacial pain as well for a more rapid differential diagnosis.
Obviously, the purpose of this article is also to challenge some of the current scientific assumptions. Even though the route is difficult and complex, further studies will be necessary, either of randomised types or of case reports analysis and considerable courage in changing such philosophies will be needed to confirm the validity of the organic normalisation factor here presented.
- ↑ Reaz MB, Hussain MS, Mohd-Yasin F, «Techniques of EMG signal analysis: detection, processing, classification and applications», in Biol Proced Online, Biological Procedures Online, 2006, Kraków, Poland».
PMID:16799694 - PMCID:PMC1455479
DOI:10.1251/bpo115 - Corrected - ↑ Masci C, Ciarrocchi I, Spadaro A, Necozione S, Marci MC, Monaco A, «Does orthodontic treatment provide a real functional improvement? A case control study», in BMC Oral Health».
PMID:24152806 - PMCID:PMC3827987
DOI:10.1186/1472-6831-13-57
This is an Open Access resource! - ↑ Wieczorek A, Loster J, Loster BW, «Relationship between occlusal force distribution and the activity of masseter and anterior temporalis muscles in asymptomatic young adults», in BioMed Res Int, 2013».
PMID:23509713 - PMCID:PMC3591202
DOI:10.1155/2013/354017
This is an Open Access resource! - ↑ Forrester SE, Allen SJ, Presswood RG, Toy AC, Pain MT, «Neuromuscular function in healthy occlusion», in J Oral Rehabil, School of Sport, Exercise and Health Sciences, Loughborough University, Loughborough, 2010, Loughborough, Leicestershire, UK».
PMID:20492437
DOI:10.1111/j.1365-2842.2010.02097.x - ↑ Hugger A, Hugger S, Schindler HJ, «Surface electromyography of the masticatory muscles for application in dental practice. Current evidence and future developments», in Int J Comput Dent, Quintessenz Verlags-GmbH, 2008, Berlin, Deutschland».
PMID:19119545 - ↑ Zhou CY, Yang ZH, Feng HL, «Short-term and long-term effects of occlusal rehabilitation on the co-contractration patterns of the electromyography of masticatory muscles», Beijing Da Xue Xue Bao Yi Xue Ban, 2008, Beijing, P.R. of China».
PMID:18560464 [Chinese] - ↑ Moazzam AA, Habibian M (2012) Patients appearing to dental professionals with orofacial pain arising from intracranial tumors: a literature review. Oral Surg Oral Med Oral Pathol Oral Radiol 114: 749-755.
- ↑ Frisardi G, Iani C, Sau G, Frisardi F, Leornadis C, et al. (2013) A relationship between bruxism and orofacial-dystonia? A trigeminal electrophysiological approach in a case report of pineal cavernoma. Behav Brain Funct 9: 41.
- ↑ Farina D, Merletti R, Enoka RM ((2004) The extraction of neural strategies from the surface EMG. J Appl Physiol 96: 1486-1495.
- ↑ Lehman GJ, McGill SM (1999) The importance of normalization in the interpretation of surface electromyography: a proof of principle. J Manipulative Physiol Ther 22: 444-446.
- ↑ Viitasalo JH, Komi PV (1977) Signal characteristics of EMG during fatigue. Eur J Appl Physiol Occup Physiol 37: 111-121.
- ↑ Viitasalo JT, Komi PV (1978) Interrelationships of EMG signal characteristics at different levels of muscle tension and during fatigue. Electromyogr Clin Neurophysiol 18: 167-178.
- ↑ Enoka RM, Robinson GA, Kossev AR (1988) A stable, selective electrode for recording single motor-unit potentials in humans. Exp Neurol 99: 761-764.
- ↑ van der Hoeven JH, van Weerden TW, Zwarts MJ (1993) Long-lasting supernormal conduction velocity after sustained maximal isometric contraction in human muscle. Muscle Nerve 16: 312-320.
- ↑ Linssen WH, Stegeman DF, Joosten EM, van’t Hof MA, Binkhorst RA, et al. (1993) Variability and interrelationships of surface EMG parameters during local muscle fatigue. Muscle Nerve 16: 849-856.
- ↑ Barton PM, Hayes KC (1996) Neck flexor muscle strength, efficiency, and relaxation times in normal subjects and subjects with unilateral neck pain and headache. Arch Phys Med Rehabil 77: 680-687.
- ↑ Carpentier A, Duchateau J, Hainaut K (2001) Motor unit behaviour and contractile changes during fatigue in the human first dorsal interosseus. J Physiol 534: 903-912.
- ↑ Merton PA, Morton HB (1980) Stimulation of the cerebral cortex in the intact human subject. Nature 285: 227.
- ↑ Barker AT, Jalinous R, Freeston IL (1985) Non-invasive magnetic stimulation of human motor cortex. Lancet 1: 1106-1107.
- ↑ Cruccu G, Berardelli A, Inghilleri M, Manfredi M (1989) Functional organization of the trigeminal motor system in man. A neurophysiological study. Brain 112: 1333-1350.
- ↑ Dworkin SF, LeResche L (1992) Research diagnostic criteria for temporomandibular disorders: review, criteria, examinations and specifications, critique. J Craniomandib Disord 6: 301-355.
- ↑ Frisardi G (1992) The use of transcranial stimulation in the fabrication of an occlusal splint. J Prosthet Dent 68: 355-360.
- ↑ Frisardi G, Ravazzani P, Tognola G, Grandori F (1997) Electric versus magnetic transcranial stimulation of the trigeminal system in healthy subjects. Clinical applications in gnathology. J Oral Rehabil 24: 920-928.
- ↑ IEC60601-2-40 (1998) Medical electrical equipment: Particular requirements for the safety of electromyographs and evoked response equipment.
- ↑ Jump up to: 25.0 25.1 Windhoff M, Opitz A, Thielscher A (2013) Electric field calculations in brain stimulation based on finite elements: an optimized processing pipeline for the generation and usage of accurate individual head models. Hum Brain Mapp 34: 923-935.
- ↑ Jump up to: 26.0 26.1 Thielscher A, Opitz A, Windhoff M (2011) Impact of the gyral geometry on the electric field induced by transcranial magnetic stimulation. Neuroimage 54: 234-243.
- ↑ Jump up to: 27.0 27.1 Opitz A, Windhoff M, Heidemann RM, Turner R, Thielscher A (2011) How the brain tissue shapes the electric field induced by transcranial magnetic stimulation. Neuroimage 58: 849-859.
- ↑ Jump up to: 28.0 28.1 Akdenur B, Okkesum S, Kara S, Gunes S (2009) Correlation- and covariance- supported normalization method for estimating orthodontic trainer treatment for clenching activity. Proc Inst Mech Eng H 223: 991-1001.
- ↑ Jump up to: 29.0 29.1 29.2 Kara S, Dirgenali F, Okkesim S (2006) Detection of gastric dysrhythmia using WT and ANN in diabetic gastroparesis patients. Comput Biol Med 36: 276-290.
- ↑ Jump up to: 30.0 30.1 30.2 Clarys JP, Cabri J (1993) Electromyography and the study of sports movements: a review. J Sports Sci 11: 379-448.
- ↑ Allison GT, Godfrey P, Robinson G (1998) EMG signal amplitude assessment during abdominal bracing and hollowing. J Electromyogr Kinesiol 8: 51-57.
- ↑ Yang JF, Winter DA (1984) Electromyographic amplitude normalization methods: improving their sensitivity as diagnostic tools in gait analysis. Arch Phys Med Rehabil 65: 517-521.
- ↑ Calder KM, Hall LA, Lester SM, Inglis JG, Gabriel DA (2005) Reliability of the biceps brachii M-wave. J Neuroeng Rehabil 2: 33.
- ↑ Lund JP, Lamarre Y, Lavigne G, Duquet G (1983) Human jaw reflexes. Adv Neurol 39: 739-755.
- ↑ Murray GM, Klineberg IJ (1984) A standardized system for evoking reflexes in human jaw elevator muscles. J Oral Rehabil 11: 361-372.
- ↑ Cruccu G, Frisardi G, van Steenberghe D (1992) Side asymmetry of the jaw jerk in human craniomandibular dysfunction. Arch Oral Biol 37: 257-262.
- ↑ Koutris M, Naeije M, Lobbezoo F, Wang K, Arendt-Nielsen L, et al. (2010) Normalization reduces the spatial dependency of the jaw-stretch reflex activity in the human masseter muscle. Muscle Nerve 41: 78-84.
- ↑ Jump up to: 38.0 38.1 Arabadzhiev TI, Dimitrov VG, Dimitrova NA, Dimitrov GV (2010) Interpretation of EMG integral or RMS and estimates of “neuromuscular efficiency” can be misleading in fatiguing contraction. J Electromyogr Kinesiol 20: 223-232.
- ↑ Bonato P, Roy SH, Knaflitz M, De Luca CJ (2001) Time-frequency parameters of the surface myoelectric signal for assessing muscle fatigue during cyclic dynamic contractions. IEEE Trans Biomed Eng 48: 745-753.
- ↑ Xie HB, Guo JY, Zheng YP (2010) Fuzzy approximate entropy analysis of chaotic and natural complex systems: detecting muscle fatigue using electromyography signals. Ann Biomed Eng 38: 1483-1496.
- ↑ Inghilleri M, Berardelli A, Cruccu G, Priori A, Manfredi M (1989) Corticospinal potentials after transcranial stimulation in humans. J Neurol Neurosurg Psychiatry 52: 970-974.
- ↑ Cruccu G, Iannetti GD, Marx JJ, Thoemke F, Truini A, et al. (2005) Brainstem reflex circuits revisited. Brain 128: 386-394.
- ↑ Kennelly KD (2012) Electrodiagnostic approach to cranial neuropathies. Neurol Clin 30: 661-684.
- ↑ Frisardi G, Chessa G, Sau G, Frisardi F (2010) Trigeminal electrophysiology: a 2 x 2 matrix model for differential diagnosis between temporomandibular disorders and orofacial pain. BMC Musculoskelet Disord 11: 141.
- ↑ Hoshino Y, Ueno Y, Shimura H, Miyamoto N, Watanabe M, et al. (2013) Marchiafava-Bignami disease mimics motor neuron disease: case report. BMC Neurol 13: 208.
- ↑ Varela H, Rubin DI (2009) Facial and trigeminal neuropathies as the initial manifestation of chronic inflammatory demyelinating polyradiculopathy. J Clin Neuromuscul Dis 10: 194-198.
- ↑ Norlinah IM, Bhatia KP, Ostergaard K, Howard R, Arabia G, et al. (2007) Primary lateral sclerosis mimicking atypical parkinsonism. Mov Disord 22: 2057-2062.
- ↑ Shigenaga Y, Yoshida A, Mitsuhiro Y, Tsuru K, Doe K (1988) Morphological and functional properties of trigeminal nucleus oralis neurons projecting to the trigeminal motor nucleus of the cat. Brain Res 461: 143-149.
- ↑ Nakamura Y, Nagashima H, Mori S (1973) Bilateral effects of the afferent impulses from the masseteric muscle on the trigeminal motoneuron of the cat. Brain Res 57: 15-27.
- ↑ Yoshida A, Yamamoto M, Moritani M, Fukami H, Bae YC, et al. (2005) Bilateral projection of functionally characterized trigeminal oralis neurons to trigeminal motoneurons in cats. Brain Res 1036: 208-212.
- ↑ McCollum G (2007) Spatial symmetry groups as sensorimotor guidelines. J Vestib Res 17: 347-359.
- ↑ Foster IZ, Hanes DA, Barmack NH, McCollum G (2007) Spatial symmetries in vestibular projections to the uvula-nodulus. Biol Cybern 96: 439-453.
- ↑ Mezzarane RA, Kohn AF (2002) Bilateral soleus H-reflexes in humans elicited by simultaneous trains of stimuli: symmetry, variability, and covariance. J Neurophysiol 87: 2074-2083.
- ↑ Deriu F, Ortu E, Capobianco S, Giaconi E, Melis F, et al. (2007) Origin of sound- evoked EMG responses in human masseter muscles. J Physiol 580: 195-209.
particularly focusing on the field of the neurophysiology of the masticatory system