Difference between revisions of "Fuzzy logic language/it"
(Created page with "cosa indica il simbolo <math>\mid</math> (tale che)") |
(Created page with "Il 'Support set' rappresenta i valori del predicato ritenuti '''possibili''', mentre il 'core' rappresenta quelli ritenuti più '''plausibili'''") Tags: Mobile web edit Mobile edit |
||
| (14 intermediate revisions by 2 users not shown) | |||
| Line 4: | Line 4: | ||
[[File:Fuzzy1.jpg|left|250px]] | [[File:Fuzzy1.jpg|left|250px]] | ||
In questo capitolo parleremo della ''logica fuzzy''. Si chiama ''fuzzy'' perché è caratterizzata da una gradualità: | In questo capitolo parleremo della ''logica fuzzy''. Si chiama ''fuzzy'' perché è caratterizzata da una gradualità: a un oggetto si può attribuire una qualità che può avere ''vari gradi di verità''. | ||
Nella prima parte di questo capitolo, verrà discusso concettualmente il significato della verità graduata, mentre nella seconda parte, ci addentreremo nel formalismo matematico introducendo la funzione di appartenenza <math>\mu_{\displaystyle {\tilde {A}}}(x)</math>: l'elemento che ci permette di sintetizzare matematicamente le sfumature di questa logica del linguaggio. È stato possibile dimostrare che con il ragionamento 'fuzzy', a differenza delle precedenti logiche del linguaggio, le diagnosi mostrano meno incertezza. Nonostante questo, però, si sente ancora la necessità di raffinare ulteriormente il metodo linguistico e di arricchirlo con altre 'logiche'..{{ArtBy| | Nella prima parte di questo capitolo, verrà discusso concettualmente il significato della verità graduata, mentre nella seconda parte, ci addentreremo nel formalismo matematico introducendo la funzione di appartenenza <math>\mu_{\displaystyle {\tilde {A}}}(x)</math>: l'elemento che ci permette di sintetizzare matematicamente le sfumature di questa logica del linguaggio. È stato possibile dimostrare che con il ragionamento 'fuzzy', a differenza delle precedenti logiche del linguaggio, le diagnosi mostrano meno incertezza. Nonostante questo, però, si sente ancora la necessità di raffinare ulteriormente il metodo linguistico e di arricchirlo con altre 'logiche'..{{ArtBy| | ||
| Line 103: | Line 103: | ||
*Appartenenza: rappresentato dal simbolo <math>\in </math> (appartenenza), - per esempio il numero 13 appartiene all'insieme dei numeri dispari <math>\in </math> <math>13\in Odd </math> | *Appartenenza: rappresentato dal simbolo <math>\in </math> (appartenenza), - per esempio il numero 13 appartiene all'insieme dei numeri dispari <math>\in </math> <math>13\in Odd </math> | ||
*Non appartenenza: rappresentato dal simbolo <math>\notin </math> (Non appartiene) | *Non appartenenza: rappresentato dal simbolo <math>\notin </math> (Non appartiene) | ||
*Inclusione: | *Inclusione: Rappresentato dal simbolo<math>\subset</math> (is content), - (è contenuto), - ad esempio l'intero <math>A</math> è contenuto all'interno dell'insieme più grande <math>U</math>, <math>A \subset U</math> (in questo caso si dice che <math>A</math> è un subset di <math>U</math>) | ||
*Quantificatore universale, che è indicato dal simbolo <math>\forall</math> (per ciascuno) | *Quantificatore universale, che è indicato dal simbolo <math>\forall</math> (per ciascuno) | ||
*Dimostrazione, cosa indica il simbolo <math>\mid</math> (tale che) | *Dimostrazione, cosa indica il simbolo <math>\mid</math> (tale che) | ||
=== | ===Operatori di insiemi=== | ||
Dato l'intero universo <math>U</math> indichiamo con <math>x</math> il suo elemento generico in modo che <math>x \in U</math>; quindi, consideriamo due sottoinsiemi <math>A</math> and <math>B</math> interni a <math>U</math> cosicché <math>A \subset U</math> e <math>B \subset U</math> | |||
{| | {| | ||
|[[File:Venn0111.svg|left|80px]] | |[[File:Venn0111.svg|left|80px]] | ||
|'''Unione:''' | |'''Unione:''' rappresentati dal simbolo <math>\cup</math>, indica l'unione di due sets <math>A</math> e <math>B</math> <math>(A\cup B)</math>. È definito da tutti gli elementi che ne fanno parte <math>A</math> e <math>B</math> o ambedue: | ||
<math>(A\cup B)=\{\forall x\in U \mid x\in A \land x\in B\}</math> | <math>(A\cup B)=\{\forall x\in U \mid x\in A \land x\in B\}</math> | ||
|- | |- | ||
|[[File:Venn0001.svg|sinistra|80px]] | |[[File:Venn0001.svg|sinistra|80px]] | ||
|'''Intersezione:''' | |'''Intersezione:''' rappresentata dal simbolo <math>\cap</math>, indica gli elementi appartenenti a entrambi gli insiemi: | ||
<math>(A\cap B)=\{\forall x\in U \mid x\in A \lor x\in B\}</math> | <math>(A\cap B)=\{\forall x\in U \mid x\in A \lor x\in B\}</math> | ||
|- | |- | ||
|[[File:Venn0010.svg|left|80px]] | |[[File:Venn0010.svg|left|80px]] | ||
|'''Differenza:''' | |'''Differenza:''' rappresentata dal simbolo <math>-</math>, per esempio <math>A-B</math> mostra che tutti gli elementi di <math>A</math> tranne quelli condivisi con <math>B</math> | ||
|- | |- | ||
|[[File:Venn1000.svg|left|80px]] | |[[File:Venn1000.svg|left|80px]] | ||
|''' | |'''Complementarità:''' rappresentato da una barra sopra il nome del termine, indica da <math>\bar{A}</math> la complementarità di <math>A</math>, cioè, l'insieme degli elementi che appartengono all'intero universo eccetto quelli di <math>A</math>, in formule: <math>\bar{A}=U-A</math><br /> | ||
|} | |} | ||
La teoria della logica del linguaggio fuzzy è un'estensione della teoria classica degli insiemi in cui, tuttavia, i principi di non contraddizione e il terzo escluso non sono validi. Ricordiamoci nella logica classica, dato l'insieme <math>A</math> e la propria complementarità <math>\bar{A}</math>, il principio di non contraddizione afferma che se un elemento appartiene al tutto <math>A</math> non può contemporaneamente appartenere anche al suo complementare <math>\bar{A}</math>; secondo il principio del terzo escluso, invece, l'unione di un tutto <math>A</math> e la propria complementarità <math>\bar{A}</math> costituisce l'universo completo <math>U</math>. | |||
In altre parole, se un elemento non appartiene al tutto, deve necessariamente appartenere al suo complementare. | |||
== | ==Fuzzy set <math>\tilde{A}</math> e funzione di appartenenza <math>\mu_{\displaystyle {\tilde {A}}}(x)</math>== | ||
Scegliamo - come formalismo - di rappresentare un insieme fuzzy con la 'tilde':<math>\tilde{A}</math>. Un insieme fuzzy è un insieme in cui gli elementi hanno un 'grado' di appartenenza (coerente con la logica fuzzy): alcuni possono essere inclusi nell'insieme al 100%, altri in percentuali inferiori. | |||
Rappresentare matematicamente questo grado di appartenenza è la funzione <math>\mu_{\displaystyle {\tilde {A}}}(x)</math> chiamato ''''Funzione di Appartenenza''''. La funzionen <math>\mu_{\displaystyle {\tilde {A}}}(x)</math> è una funzione continua definita nell'intervallo <math>[0;1]</math>dove è: | |||
*<math>\mu_ {\tilde {A}}(x) = 1\rightarrow </math> | *<math>\mu_ {\tilde {A}}(x) = 1\rightarrow </math> se <math>x</math> è totalmente contenuta in <math>A</math> (questi punti sono chiamati 'nucleo', indicano valori predicativi <u>plausible</u>). | ||
*<math>\mu_ {\tilde {A}}(x) = 0\rightarrow </math> | *<math>\mu_ {\tilde {A}}(x) = 0\rightarrow </math> se <math>x</math> non è contenuto in <math>A</math> | ||
*<math>0<\mu_ {\tilde {A}}(x) < 1 \;\rightarrow </math> | *<math>0<\mu_ {\tilde {A}}(x) < 1 \;\rightarrow </math> se <math>x</math> è parzialmente contenuto in <math>A</math> (questi punti sono chiamati 'supporto', indicano i valori del predicato <u>possible</u>). | ||
La rappresentazione grafica della funzione <math>\mu_{\displaystyle {\tilde {A}}}(x)</math> può essere variato; da quelli con linee lineari (triangolari, trapezoidali) a quelli a forma di campana o 'S' (sigmoidale) come rappresentato in Figura 1, che racchiude l'intero concetto grafico della funzione di appartenenza.<ref>{{Cite book | |||
| autore = Zhang W | | autore = Zhang W | ||
| autore2 = Yang J | | autore2 = Yang J | ||
| Line 184: | Line 184: | ||
| OCLC = | | OCLC = | ||
}}</ref> | }}</ref> | ||
[[File:Fuzzy_crisp.svg|alt=|left|thumb|400px|''' | [[File:Fuzzy_crisp.svg|alt=|left|thumb|400px|'''Figura 1:''' Tipi di grafici per la funzione di appartenenza.]] | ||
Il '''support set''' di un fuzzy set è definito come la zona in cui risulta il grado di appartenenza <math>0<\mu_ {\tilde {A}}(x) < 1</math>; il '''core''' è invece definito come l'area in cui assume valore il grado di appartenenza <math>\mu_ {\tilde {A}}(x) = 1</math> | |||
Il 'Support set' rappresenta i valori del predicato ritenuti '''possibili''', mentre il 'core' rappresenta quelli ritenuti più '''plausibili'''. | |||
Se <math>{A}</math> rappresentato un insieme nel senso ordinario del termine o della logica linguistica classica precedentemente descritta, la sua funzione di appartenenza poteva assumere solo dei valori <math>1</math> oppure <math>0</math>, <math>\mu_{\displaystyle {{A}}}(x)= 1 \; \lor \;\mu_{\displaystyle {{A}}}(x)= 0</math> a seconda che l'elemento <math>x</math> appartiene al tutto o meno, come considerato. La figura 2 mostra una rappresentazione grafica del concetto nitido (rigidamente definito) o sfocato di appartenenza, che richiama chiaramente le considerazioni di Smuts.<ref name=":0">•SMUTS J.C. 1926, [[wikipedia:Holism_and_Evolution|Olismo ed Evoluzione]], London: Macmillan.</ref> | |||
Torniamo al caso specifico della nostra Mary Poppins, in cui vediamo una discrepanza tra le affermazioni del dentista e del neurologo e cerchiamo un confronto tra logica classica e logica fuzzy: | |||
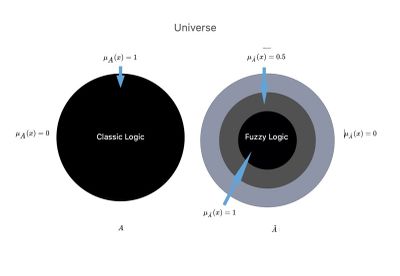
[[File:Fuzzy1.jpg|thumb|400x400px|''' | [[File:Fuzzy1.jpg|thumb|400x400px|'''Figura 2:''' Rappresentazione del confronto tra ensemble classico e fuzzy.]] | ||
''' | '''Figura 2:''' Immaginiamo l'universo della scienza <math>U</math> in cui ci sono due mondi o contesti paralleli, <math>{A}</math> e <math>\tilde{A}</math>. | ||
<math>{A}=</math> | <math>{A}=</math> Nel contesto scientifico, il cosiddetto 'nitido', e ci siamo convertiti nella 'logica'' del 'Linguaggio Classico'', in cui il medico ha un background scientifico assoluto <math>KB</math> con una chiara linea di demarcazione che abbiamo nominato <math>KB_c</math>. | ||
<math>\tilde{A}=</math> In | <math>\tilde{A}=</math> In un altro contesto scientifico chiamato "logica fuzzy", e in cui c'è un'unione tra i sottoinsiemi <math>{A}</math> in <math>\tilde{A}</math> che possiamo arrivare a dire: unione tra <math>KB_c</math>. | ||
Noteremo notevolmente le seguenti deduzioni: | |||
*''' | *'''Logica Classica''' nel 'contesto dentale' <math>{A}</math> in cui solo un processo logico che dà come risultati <math>\mu_{\displaystyle {{A}}}(x)= 1 </math> sarà possibile, o <math>\mu_{\displaystyle {{A}}}(x)= 0 </math> essendo la gamma di dati <math>D=\{\delta_1,\dots,\delta_4\}</math> ridotto alla conoscenza di base <math>KB</math> nel set <math>{A}</math>. Ciò significa che al di fuori del mondo dentale c'è un vuoto e che il termine di teoria degli insiemi è scritto proprio <math>\mu_{\displaystyle {{A}}}(x)= 0 </math> e che è sinonimo di un'alto range di: | ||
<br />{{q2| | <br />{{q2|errori nella diagnosi differenziale|}} | ||
*''' | *'''Logica fuzzy''' in un contesto dentale <math>\tilde{A}</math> in cui sono rappresentati, al di là delle conoscenze di base, <math>KB</math> del contesto dentale anche quelli parzialmente acquisiti dal contesto neurofisiologico <math>0<\mu_ {\tilde {A}}(x) < 1</math> avrà la prerogativa di restituire un risultato <math>\mu_\tilde{A}(x)= 1 | ||
</math> | </math> ed un risultato <math>0<\mu_ {\tilde {A}}(x) < 1</math> poiché la conoscenza di base <math>KB</math> che a questo punto è rappresentato dall'unione di <math>KB_c</math> dei contesti dentali e neurologici. Il risultato di questa implementazione scientifico-clinica dell'odontoiatria consentirebbe a {{q2|Riduzione dell'errore nella diagnostica differenziale|}} | ||
== | ==Considerazioni finali== | ||
Gli argomenti che potevano distrarre l'attenzione del lettore erano, infatti, essenziali per dimostrare il messaggio. Normalmente, infatti, quando una mente più o meno brillante si permette di lanciare un sasso nello stagno della Scienza, si genera un'onda d'urto, tipica del periodo della scienza straordinaria di Kuhn, contro la quale remano contro la maggior parte dei membri della comunità scientifica internazionale. In buona fede, possiamo affermare che questo fenomeno – per quanto riguarda gli argomenti qui trattati – è ben rappresentato nella premessa all'inizio del capitolo. | |||
In | In questi capitoli, infatti, è stato affrontato un tema fondamentale per la scienza: la rivalutazione, il peso specifico a cui è sempre stato attribuito <math>P-value</math>, consapevolezza dei contesti scientifico/clinici <math>KB_c</math>, aver intrapreso un percorso di Fuzzy Logic più elastico rispetto a quello Classico, rendendosi conto dell'estrema importanza di <math>KB</math> e infine l'unione di contesti <math>KB_c</math> per aumentare la sua capacità diagnostica.<ref>Mehrdad Farzandipour, Ehsan Nabovati, Soheila Saeedi, Esmaeil Fakharian. [https://pubmed.ncbi.nlm.nih.gov/30119845/ Fuzzy decision support systems to diagnose musculoskeletal disorders: A systematic literature review] . Comput Methods Programs Biomed. 2018 Sep;163:101-109. doi: 10.1016/j.cmpb.2018.06.002. Epub 2018 Jun 6.</ref><ref>Long Huang, Shaohua Xu, Kun Liu, Ruiping Yang, Lu Wu. [https://pubmed.ncbi.nlm.nih.gov/34257635/ A Fuzzy Radial Basis Adaptive Inference Network and Its Application to Time-Varying Signal Classification] . Comput Intell Neurosci, 2021 Jun 23;2021:5528291.<br>doi: 10.1155/2021/5528291.eCollection 2021.</ref> | ||
Nel prossimo capitolo saremo pronti per intraprendere un percorso altrettanto affascinante: ci porterà nel contesto di una linguaggio di logica di sistema, e ci permetterà di approfondire le nostre conoscenze, non più solo nella semeiotica clinica, ma nella comprensione delle funzioni di sistema (di recente è in corso di valutazione nelle discipline neuromotorie per il morbo di Parkinson).<ref>Mehrbakhsh Nilashi, Othman Ibrahim, Ali Ahani. [https://pubmed.ncbi.nlm.nih.gov/27686748/ Accuracy Improvement for Predicting Parkinson's Disease Progression.] Sci Rep. 2016 Sep 30;6:34181. | |||
doi: 10.1038/srep34181.</ref> | |||
In Masticationpedia, ovviamente, riporteremo l'argomento 'System Inference' nell'ambito del sistema masticatorio come potremmo leggere nel prossimo capitolo intitolato 'System logic'. | |||
{{Btnav|The logic of probabilistic language|Introduction}} | {{Btnav|The logic of probabilistic language|Introduction}} | ||
Latest revision as of 15:28, 3 April 2022
In questo capitolo parleremo della logica fuzzy. Si chiama fuzzy perché è caratterizzata da una gradualità: a un oggetto si può attribuire una qualità che può avere vari gradi di verità.
Nella prima parte di questo capitolo, verrà discusso concettualmente il significato della verità graduata, mentre nella seconda parte, ci addentreremo nel formalismo matematico introducendo la funzione di appartenenza : l'elemento che ci permette di sintetizzare matematicamente le sfumature di questa logica del linguaggio. È stato possibile dimostrare che con il ragionamento 'fuzzy', a differenza delle precedenti logiche del linguaggio, le diagnosi mostrano meno incertezza. Nonostante questo, però, si sente ancora la necessità di raffinare ulteriormente il metodo linguistico e di arricchirlo con altre 'logiche'..
Introduzione
Siamo arrivati a questo punto perché, come colleghi, ci troviamo molto spesso di fronte a responsabilità e decisioni che sono molto difficili da prendere e entrano in gioco questioni come la coscienza, intelligenza ed umiltà. In tale situazione, però, ci troviamo di fronte a due ostacoli ugualmente difficili da gestire: quello di una (Knowledge Basis, Conoscenza di base), come l'abbiamo discussa nel capitolo 'Logica del linguaggio probabilistico', limitata nel tempo che codifichiamo in , e una limitata nel contesto specifico (). Questi due parametri dell'epistemologia caratterizzano l'epoca scientifica in cui viviamo. Inoltre, sia la che la sono variabili dipendenti della nostra filogenesi e, in particolare, della nostra plasticità concettuale e attitudine al cambiamento.[1]
(I'll give you a practical example)
Quante ricerche sono state prodotte sull'argomento "logica fuzzy"?
Pubmed risponde con 2862 articoli negli ultimi 10 anni[2][3], così che possiamo dire che il nostro è attuale ed è sufficientemente aggiornato. Tuttavia, se volessimo focalizzare l'attenzione su un argomento specifico come 'Disturbi Temporomandibolari', il database risponderà con ben 2.235 articoli. [4] Quindi, se volessimo controllare un altro argomento come 'Orofacial Pain', Pubmed ci dà 1.986 articoli.[5] Questo significa che il per questi tre argomenti negli ultimi 10 anni è stato sufficientemente aggiornato.
Se, ora, volessimo verificare l'interconnessione tra gli argomenti, noteremo che nei contesti sarà il seguente:
- 'Disturbi temporomandibolari E dolore orofacciale' 9 articoli negli ultimi 10 anni[6]
- 'Disturbi temporomandibolari E Dolore orofacciale E Logica fuzzy' 0 articoli negli ultimi 10 anni[7]
L'esempio indica che il è relativamente aggiornato individualmente per i tre argomenti, mentre diminuisce drasticamente quando gli argomenti tra i contesti sono uniti e specificamente a 9 articoli per il punto 1 e anche a 0 articoli per il punto 2. Perciò, la è una variabile dipendente dal tempo mentre la è una variabile cognitiva dipendente dalla nostra attitudine al progresso della scienza, come già accennato, tra l'altro, nel capitolo "Introduzione".
(Aspetta e vedrai)
Abbiamo concluso il capitolo precedente affermando che la logica di un linguaggio classico e successivamente la logica probabilistica ci hanno aiutato molto nel progresso della scienza medica e della diagnostica, ma implicitamente portano in sé i limiti della propria logica di linguaggio, che limita la visione dell'universo biologico.. Abbiamo anche verificato che con la logica di un linguaggio classico, per così dire aristotelico, la sintassi logica che ne deriva nella diagnostica della nostra Mary Poppins limita, di fatto, la conclusione clinica..
(vedi capitolo Classical Language's Logic),
afferma che: "qualsiasi paziente normale che è positivo all'esame radiografico della ATM soffre di Disordini Temporomandibolari (DTM), come diretta conseguenza avendo Mary Poppins un referto positivo radiologico positiva della ATM (ed essendo anche una paziente "normale") , allora anche Mary Poppins è affetta da DTM
La limitazione del percorso logico seguito ci ha portato a intraprendere un percorso alternativo, in cui si evita la bivalenza o la natura binaria della logica linguistica classica e si segue un modello probabilistico. Il collega dentista, infatti, ha cambiato il vocabolario e ha preferito una conclusione come:
e cioè che la nostra Mary Poppins è affetta al 95% da DTM poiché ha una degenerazione dell'articolazione temporomandibolare sostenuta dalla positività dei dati in un campione di popolazione . Tuttavia, lo abbiamo anche trovato nel processo di costruzione della logica probabilistica (Analysandum ) che ci ha permesso di formulare le suddette conclusioni diagnostiche differenziali e di scegliere quella più plausibile, c'è un elemento cruciale nell'insieme Analysand rappresentato dal termine che indica, nello specifico, una 'Base di conoscenza' del contesto su cui si costruisce la logica del linguaggio probabilistico.
Abbiamo quindi concluso che forse il collega dentista avrebbe dovuto venire a conoscenza della propria 'Incertezza Soggettiva' (colpita da DTM o Dolore Orofacciale?) nOP? e "Incertezza oggettiva" (probabilmente più influenzata da DTM o Dolore orofacciale?nOP?).
Perché siamo arrivati a queste conclusioni critiche?
Per una forma ampiamente condivisa di rappresentazione della realtà, sostenuta dalla testimonianza di figure autorevoli che ne confermano la criticità. Questo ha dato origine a una visione della realtà che, a prima vista, sembrerebbe inadatta al linguaggio medico; infatti, espressioni come "circa 2" o "moderatamente" possono suscitare legittime perplessità e sembrare un anacronistico ritorno a concetti pre-scientifici. Al contrario, però, l'uso dei numeri fuzzy o delle asserzioni permette di trattare i dati scientifici in contesti in cui non si può parlare di 'probabilità' ma solo di 'possibilità'.[8]
Verità fuzzy
Nell'ambizioso tentativo di tradurre in matematica la razionalità umana, si è pensato a metà del XX secolo di espandere il concetto di logica classica formulando la logica fuzzy. La logica fuzzy riguarda le proprietà che potremmo chiamare 'gradualità', cioè che possono essere attribuite a un oggetto con gradi diversi. Esempi sono le proprietà 'essere malato', 'avere dolore', 'essere alto', 'essere giovane', e così via.
Matematicamente, la logica fuzzy ci permette di attribuire a ciascuna proposizione un grado di verità tra and . L'esempio più classico per spiegare questo concetto è quello dell'età: si può dire che un neonato ha un 'grado di giovinezza' pari a , un diciottenne pari a, un sessantenne pari a, e così via.
Nel contesto della logica classica, invece, le affermazioni:
- un bambino di dieci anni è giovane
- un trentenne è giovane
sono entrambe vere. Tuttavia, nel caso della logica classica (che ammette solo i due dati vero o falso), questo significherebbe che il bambino e il trentenne sono ugualmente giovani. Il che è ovviamente sbagliato.
L'importanza e il fascino della logica fuzzy derivano dal fatto che è in grado di tradurre l'incertezza insita in alcuni dati del linguaggio umano in un formalismo matematico, codificando concetti 'elastici' (come quasi alto, abbastanza buono, ecc.), al fine di renderli comprensibili e gestibili dai computer.
Teoria degli insiemi
Come accennato nel capitolo precedente, il concetto base della logica fuzzy è quello della multivalenza, cioè, in termini di teoria degli insiemi, della possibilità che un oggetto possa appartenere a un insieme anche solo parzialmente e, quindi, anche a più insiemi con gradi diversi.. Ricordiamo fin dall'inizio gli elementi di base della teoria degli insiemi ordinari. Come si vedrà, in essi appaiono le espressioni formali dei principi della logica aristotelica, ricordati nel capitolo precedente..
Quantificatori
- Appartenenza: rappresentato dal simbolo (appartenenza), - per esempio il numero 13 appartiene all'insieme dei numeri dispari
- Non appartenenza: rappresentato dal simbolo (Non appartiene)
- Inclusione: Rappresentato dal simbolo (is content), - (è contenuto), - ad esempio l'intero è contenuto all'interno dell'insieme più grande , (in questo caso si dice che è un subset di )
- Quantificatore universale, che è indicato dal simbolo (per ciascuno)
- Dimostrazione, cosa indica il simbolo (tale che)
Operatori di insiemi
Dato l'intero universo indichiamo con il suo elemento generico in modo che ; quindi, consideriamo due sottoinsiemi and interni a cosicché e
La teoria della logica del linguaggio fuzzy è un'estensione della teoria classica degli insiemi in cui, tuttavia, i principi di non contraddizione e il terzo escluso non sono validi. Ricordiamoci nella logica classica, dato l'insieme e la propria complementarità , il principio di non contraddizione afferma che se un elemento appartiene al tutto non può contemporaneamente appartenere anche al suo complementare ; secondo il principio del terzo escluso, invece, l'unione di un tutto e la propria complementarità costituisce l'universo completo .
In altre parole, se un elemento non appartiene al tutto, deve necessariamente appartenere al suo complementare.
Fuzzy set e funzione di appartenenza
Scegliamo - come formalismo - di rappresentare un insieme fuzzy con la 'tilde':. Un insieme fuzzy è un insieme in cui gli elementi hanno un 'grado' di appartenenza (coerente con la logica fuzzy): alcuni possono essere inclusi nell'insieme al 100%, altri in percentuali inferiori.
Rappresentare matematicamente questo grado di appartenenza è la funzione chiamato 'Funzione di Appartenenza'. La funzionen è una funzione continua definita nell'intervallo dove è:
- se è totalmente contenuta in (questi punti sono chiamati 'nucleo', indicano valori predicativi plausible).
- se non è contenuto in
- se è parzialmente contenuto in (questi punti sono chiamati 'supporto', indicano i valori del predicato possible).
La rappresentazione grafica della funzione può essere variato; da quelli con linee lineari (triangolari, trapezoidali) a quelli a forma di campana o 'S' (sigmoidale) come rappresentato in Figura 1, che racchiude l'intero concetto grafico della funzione di appartenenza.[9][10]
Il support set di un fuzzy set è definito come la zona in cui risulta il grado di appartenenza ; il core è invece definito come l'area in cui assume valore il grado di appartenenza
Il 'Support set' rappresenta i valori del predicato ritenuti possibili, mentre il 'core' rappresenta quelli ritenuti più plausibili.
Se rappresentato un insieme nel senso ordinario del termine o della logica linguistica classica precedentemente descritta, la sua funzione di appartenenza poteva assumere solo dei valori oppure , a seconda che l'elemento appartiene al tutto o meno, come considerato. La figura 2 mostra una rappresentazione grafica del concetto nitido (rigidamente definito) o sfocato di appartenenza, che richiama chiaramente le considerazioni di Smuts.[11]
Torniamo al caso specifico della nostra Mary Poppins, in cui vediamo una discrepanza tra le affermazioni del dentista e del neurologo e cerchiamo un confronto tra logica classica e logica fuzzy:
Figura 2: Immaginiamo l'universo della scienza in cui ci sono due mondi o contesti paralleli, e .
Nel contesto scientifico, il cosiddetto 'nitido', e ci siamo convertiti nella 'logica del 'Linguaggio Classico, in cui il medico ha un background scientifico assoluto con una chiara linea di demarcazione che abbiamo nominato .
In un altro contesto scientifico chiamato "logica fuzzy", e in cui c'è un'unione tra i sottoinsiemi in che possiamo arrivare a dire: unione tra .
Noteremo notevolmente le seguenti deduzioni:
- Logica Classica nel 'contesto dentale' in cui solo un processo logico che dà come risultati sarà possibile, o essendo la gamma di dati ridotto alla conoscenza di base nel set . Ciò significa che al di fuori del mondo dentale c'è un vuoto e che il termine di teoria degli insiemi è scritto proprio e che è sinonimo di un'alto range di:
- Logica fuzzy in un contesto dentale in cui sono rappresentati, al di là delle conoscenze di base, del contesto dentale anche quelli parzialmente acquisiti dal contesto neurofisiologico avrà la prerogativa di restituire un risultato ed un risultato poiché la conoscenza di base che a questo punto è rappresentato dall'unione di dei contesti dentali e neurologici. Il risultato di questa implementazione scientifico-clinica dell'odontoiatria consentirebbe a «Riduzione dell'errore nella diagnostica differenziale»
Considerazioni finali
Gli argomenti che potevano distrarre l'attenzione del lettore erano, infatti, essenziali per dimostrare il messaggio. Normalmente, infatti, quando una mente più o meno brillante si permette di lanciare un sasso nello stagno della Scienza, si genera un'onda d'urto, tipica del periodo della scienza straordinaria di Kuhn, contro la quale remano contro la maggior parte dei membri della comunità scientifica internazionale. In buona fede, possiamo affermare che questo fenomeno – per quanto riguarda gli argomenti qui trattati – è ben rappresentato nella premessa all'inizio del capitolo.
In questi capitoli, infatti, è stato affrontato un tema fondamentale per la scienza: la rivalutazione, il peso specifico a cui è sempre stato attribuito , consapevolezza dei contesti scientifico/clinici , aver intrapreso un percorso di Fuzzy Logic più elastico rispetto a quello Classico, rendendosi conto dell'estrema importanza di e infine l'unione di contesti per aumentare la sua capacità diagnostica.[12][13]
Nel prossimo capitolo saremo pronti per intraprendere un percorso altrettanto affascinante: ci porterà nel contesto di una linguaggio di logica di sistema, e ci permetterà di approfondire le nostre conoscenze, non più solo nella semeiotica clinica, ma nella comprensione delle funzioni di sistema (di recente è in corso di valutazione nelle discipline neuromotorie per il morbo di Parkinson).[14]
In Masticationpedia, ovviamente, riporteremo l'argomento 'System Inference' nell'ambito del sistema masticatorio come potremmo leggere nel prossimo capitolo intitolato 'System logic'.
- ↑ Takeuchi S, Okuda S, «Knowledge base toward understanding actionable alterations and realizing precision oncology», in Int J Clin Oncol, 2019».
PMID:30542800 - PMCID:PMC6373253
DOI:10.1007/s10147-018-1378-0
This is an Open Access resource! - ↑ Fuzzy logic on Pubmed
- ↑ Tutte le statistiche raccolte a seguito di visite al sito Pubmed (https://pubmed.ncbi.nlm.nih.gov/). Ultimo controllo: Dicembre 2020.
- ↑ Disturbi temporomandibolari in Pubmed
- ↑ Dolore orofacciale in Pubmed
- ↑ Disturbi temporomandibolari E dolore orofacciale in Pubmed
- ↑ "Disturbi temporomandibolari E dolore orofacciale E logica fuzzy" in Pubmed
- ↑ Dubois D, Prade H, «Fundamentals of Fuzzy Sets», Kluwer Academic Publishers, 2000, Boston».
- ↑ Zhang W, Yang J, Fang Y, Chen H, Mao Y, Kumar M, «Analytical fuzzy approach to biological data analysis», in Saudi J Biol Sci, 2017».
PMID:28386181 - PMCID:PMC5372457
DOI:10.1016/j.sjbs.2017.01.027 - ↑ Lazar P, Jayapathy R, Torrents-Barrena J, Mol B, Mohanalin, Puig D, «Fuzzy-entropy threshold based on a complex wavelet denoising technique to diagnose Alzheimer disease», in Healthc Technol Lett, The Institution of Engineering and Technology, 2016».
PMID:30800318 - PMCID:PMC6371778
DOI:10.1049/htl.2016.0022 - ↑ •SMUTS J.C. 1926, Olismo ed Evoluzione, London: Macmillan.
- ↑ Mehrdad Farzandipour, Ehsan Nabovati, Soheila Saeedi, Esmaeil Fakharian. Fuzzy decision support systems to diagnose musculoskeletal disorders: A systematic literature review . Comput Methods Programs Biomed. 2018 Sep;163:101-109. doi: 10.1016/j.cmpb.2018.06.002. Epub 2018 Jun 6.
- ↑ Long Huang, Shaohua Xu, Kun Liu, Ruiping Yang, Lu Wu. A Fuzzy Radial Basis Adaptive Inference Network and Its Application to Time-Varying Signal Classification . Comput Intell Neurosci, 2021 Jun 23;2021:5528291.
doi: 10.1155/2021/5528291.eCollection 2021. - ↑ Mehrbakhsh Nilashi, Othman Ibrahim, Ali Ahani. Accuracy Improvement for Predicting Parkinson's Disease Progression. Sci Rep. 2016 Sep 30;6:34181. doi: 10.1038/srep34181.
particularly focusing on the field of the neurophysiology of the masticatory system













































![{\displaystyle [0;1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc3bf59a5da5d8181083b228c8933efbda133483)