Quantum-like modeling in biology with open quantum systems and instruments - en

Free resource

Quantum-like modeling in biology with open quantum systems and instruments

Free resource by Irina Basieva  · Andrei Khrennikov · Masanao Ozawa

Irina Basieva^a, Andrei Khrennikov^a, Masanao Ozawa^b,c

^aLinnaeus University, International Center for Mathematical Modeling in Physics and Cognitive Sciences Växjö, SE-351 95, Sweden

^bCollege of Engineering, Chubu University, 1200 Matsumoto-cho, Kasugai 487-8501, Japan

^cGraduate School of Informatics, Nagoya University, Chikusa-ku, Nagoya 464-8601, Japan

Abstracto

Presentamos el enfoque novedoso para el modelado matemático de procesos de información en biosistemas. Explora el formalismo matemático y la metodología de la teoría cuántica, especialmente la teoría de la medición cuántica. Este enfoque se conoce como de tipo cuántico y debe distinguirse del estudio de procesos físicos cuánticos genuinos en biosistemas (biofísica cuántica, cognición cuántica). Se basa en la representación de información cuántica del estado del biosistema y el modelado de su dinámica en el marco de la teoría de sistemas cuánticos abiertos. Este artículo comienza con una presentación no amigable para los físicos de la teoría de la medición cuántica, desde la formulación original de von Neumann hasta la teoría moderna de los instrumentos cuánticos. Luego, este último se aplica a combinaciones modelo de efectos cognitivos y regulación génica del metabolismo de glucosa/lactosa en la bacteria Escherichia coli. La construcción más general de los instrumentos cuánticos se basa en el esquema de medición indirecta, en el que el aparato de medición desempeña el papel del medio ambiente para un biosistema. La esencia biológica de este esquema se ilustra mediante la formalización cuántica de la teoría de la sensación-percepción de Helmholtz. Luego pasamos a la dinámica de sistemas abiertos y consideramos la ecuación maestra cuántica, concentrándonos en los procesos cuánticos de Markov. En este marco, modelamos el funcionamiento de funciones biológicas como funciones psicológicas y mutación epigenética.

Keywords

Formalismo matemático de la mecánica cuántica, Sistemas cuánticos abiertos, Instrumentos cuánticos, Dinámica cuántica de Markov, Regulación génica, Efectos psicológicos, Cognición, Mutación epigenética, Funciones biológicas

Introducción

Los métodos matemáticos estándar se desarrollaron originalmente para servir a la física clásica. El análisis real sirvió como base matemática de la mecánica newtoniana (Newton, 1687) (y posterior formalismo hamiltoniano); la mecánica estadística clásica estimuló el enfoque teórico de la medida de la teoría de la probabilidad, formalizado en la axiomática de Kolmogorov (Kolmogorov, 1933). Sin embargo, el comportamiento de los sistemas biológicos difiere esencialmente del comportamiento de los sistemas mecánicos, digamos cuerpos rígidos, moléculas de gas o fluidos. Por lo tanto, aunque las “matemáticas clásicas” aún desempeñan un papel crucial en el modelado biológico, parece que no pueden describir completamente la rica complejidad de los biosistemas y las peculiaridades de su comportamiento, en comparación con los sistemas mecánicos. Se están solicitando nuevos métodos matemáticos para modelar biosistemas.(a,b)

En este artículo, presentamos las aplicaciones del formalismo matemático de la mecánica cuántica y su metodología para modelar el comportamiento de los biosistemas. (c) Los últimos años se caracterizaron por una explosión de interés por las aplicaciones de la teoría cuántica fuera de la física, especialmente en la psicología cognitiva. toma de decisiones, procesamiento de información en el cerebro, biología molecular, genética y epigenética, y teoría de la evolución.4 Llamamos a los modelos correspondientes de tipo cuántico. No están dirigidos al modelado a nivel micro de procesos físicos cuánticos reales en biosistemas, digamos en células o cerebros (cf. con aplicaciones biológicas de la teoría física cuántica genuina Penrose 1989, Umezawa 1993, Hameroff 1994, Vitiello 1995, Vitiello 2001, Arndt et al. al., 2009, Bernroider y Summhammer 2012, Bernroider 2017). El modelado de tipo cuántico funciona desde el punto de vista de la teoría cuántica como teoría de la medición. Este es el punto de vista original de Bohr que condujo a la interpretación de Copenhague de la mecánica cuántica (ver Plotnitsky, 2009 para una presentación clara y detallada de los puntos de vista de Bohr). Una de las principales bioespecialidades es la consideración de las automedidas que los biosistemas realizan sobre sí mismos. En nuestro modelo, la capacidad de realizar automedidas se considera la característica básica de las funciones biológicas (consulte la Sección 8.2 y el artículo Khrennikov et al., 2018).

Modelos de tipo cuántico (Khrennikov, 2004b)

reflejan las características de los procesos biológicos que coinciden naturalmente con el formalismo cuántico. En dicho modelado, es útil explorar la teoría de la información cuántica, que se puede aplicar no solo al micromundo de los sistemas cuánticos. Generalmente, los sistemas que procesan información de forma cuántica no necesitan ser sistemas físicos cuánticos; en particular, pueden ser biosistemas macroscópicos. Sorprendentemente, la misma teoría matemática se puede aplicar a todas las escalas biológicas: desde proteínas, células y cerebros hasta humanos y ecosistemas; podemos hablar de biología de la información cuántica (Asano et al., 2015a ).

En el modelado de tipo cuántico, la teoría cuántica se considera como un cálculo para la predicción y transformación de probabilidades. El cálculo de probabilidad cuántica (QP) (Sección 2) difiere esencialmente del cálculo de probabilidad clásico (CP) basado en la axiomática de Kolmogorov (Kolmogorov, 1933).En CP, los estados de los sistemas aleatorios están representados por medidas de probabilidad y los observables por variables aleatorias; en QP, los estados de los sistemas aleatorios se representan mediante vectores normalizados en un espacio de Hilbert complejo (estados puros) o, en general, mediante operadores de densidad (estados mixtos).5 Las superposiciones representadas por estados puros se utilizan para modelar la incertidumbre que aún no ha sido resuelta por una medición. El uso de superposiciones en biología se ilustra en la Fig. 1 (consulte la Sección 10 y el artículo Khrennikov et al., 2018)

para el modelo correspondiente). La actualización QP resultante de una observación se basa en el postulado de proyección o transformaciones más generales de estados cuánticos — en el marco de la teoría de instrumentos cuánticos (Davies y Lewis, 1970, Davies, 1976, Ozawa, 1984, Yuen, 1987, Ozawa , 1997, Ozawa, 2004, Okamura y Ozawa, 2016) (Sección 3).

Fig. 1. Illustration for quantum-like representation of uncertainty generated by neuron’s action potential (originally published in Khrennikov et al. (2018)).

Hacemos hincapié en que el modelado de tipo cuántico eleva el papel de la conveniencia y la simplicidad de la representación cuántica de estados y observables. (Ignoramos pragmáticamente el problema de la interrelación de CP y QP). En particular, el espacio de estado cuántico tiene una estructura lineal y los modelos lineales son más simples. La transición de la dinámica no lineal clásica de los procesos electroquímicos en biosistemas a la dinámica lineal cuántica esencialmente acelera la evolución del estado (Sección 8.4). Sin embargo, en este marco, "estado" es el estado de información cuántica de un biosistema utilizado para el procesamiento de la incertidumbre cuántica especial (Sección 8.2).

Observaciones

En los libros de texto sobre mecánica cuántica, se suele señalar que la principal característica distintiva de la teoría cuántica es la presencia de observables incompatibles. Recordemos que dos observables $A$ $B$ y  son incompatibles si es imposible asignarles valores conjuntamente. En el modelo probabilístico, esto lleva a la imposibilidad de determinar su distribución de probabilidad conjunta (JPD). Los ejemplos básicos de observables incompatibles son la posición y el momento de un sistema cuántico, o las proyecciones de espín (o polarización) en diferentes ejes. En el formalismo matemático, la incompatibilidad se describe como la no conmutatividad de los operadores hermitianos. ${\hat {A}}$ y ${\hat {B}}$ representando observables, i.e., $[{\hat {A}},{\hat {B}}]\neq 0$

Aquí nos referimos al modelo original y aún básico y ampliamente utilizado de observables cuánticos, Von Neumann 1955 (Sección 3.2).

La incompatibilidad-no conmutatividad se usa ampliamente en la física cuántica y los observables físicos básicos, como las proyecciones de posición y momento, espín y polarización, se representan tradicionalmente en este paradigma, mediante operadores hermitianos. También señalamos numerosas aplicaciones de este enfoque a la cognición, la psicología, la toma de decisiones (Khrennikov, 2004a, Busemeyer y Bruza, 2012, Bagarello, 2019) (ver especialmente el artículo (Bagarello et al., 2018) dedicado a la cuantificación de la Relaciones de incertidumbre de Heisenberg en la toma de decisiones). Aún así, puede que no sea lo suficientemente general para nuestro propósito: para el modelado de tipo cuántico en biología, ningún tipo de bioestadística no clásica se puede delegar fácilmente al modelo de observaciones de von Neumann. Por ejemplo, ni siquiera los efectos cognitivos más básicos pueden describirse de manera coherente con el modelo de observación estándar (Khrennikov et al., 2014, Basieva y Khrennikov, 2015).

Exploraremos teorías más generales de las observaciones basadas en instrumentos cuánticos (Davies y Lewis, 1970, Davies, 1976, Ozawa, 1984, Yuen, 1987, Ozawa, 1997, Ozawa, 2004, Okamura y Ozawa, 2016) y encontraremos herramientas útiles para aplicaciones al modelado de efectos cognitivos (Ozawa y Khrennikov, 2020a, Ozawa y Khrennikov, 2020b). Discutiremos esta pregunta en la Sección 3 y la ilustraremos con ejemplos de cognición y biología molecular en las Secciones 6, 7. En el marco de la teoría cuántica de instrumentos, el punto crucial no es la conmutatividad frente a la no conmutatividad de los operadores que representan simbólicamente observables, sino la forma matemática de la transformación de estado resultante de la acción posterior de la (auto)observación. En el enfoque estándar, esta transformación viene dada por una proyección ortogonal en el subespacio de vectores propios correspondientes a la salida de la observación. Este es el postulado de proyección. En la teoría cuántica de instrumentos, las transformaciones de estado son más generales.

El cálculo de instrumentos cuánticos está estrechamente relacionado con la teoría de los sistemas cuánticos abiertos (Ingarden et al., 1997), sistemas cuánticos que interactúan con los entornos. Hacemos notar que en algunas situaciones, los sistemas físicos cuánticos pueden requerir (al menos aproximadamente) aislados. Sin embargo, los biosistemas son muy abiertos. Como destaca Schrödinger (1944), un biosistema completamente aislado está muerto. Esto último explica por qué la teoría de los sistemas cuánticos abiertos y, en particular, el cálculo de instrumentos cuánticos juegan el papel básico en las aplicaciones a la biología, como el aparato matemático de la biología cuántica de la información (Asano et al., 2015a).

Dentro de la teoría de los sistemas cuánticos abiertos, modelamos la evolución epigenética (Asano et al., 2012b, Asano et al., 2015b) (Secciones 9, 11.2) y el desempeño de las funciones psicológicas (cognitivas) realizadas por el cerebro (Asano et al., 2015b). 2011, Asano et al., 2015b, Khrennikov et al., 2018

Para biólogos matemáticamente suficientemente bien educados, pero sin conocimiento en física, podemos recomendar un libro (Khrennikov, 2016a) que combina las presentaciones de CP y QP con una breve introducción al formalismo cuántico, incluida la teoría de los instrumentos cuánticos y las probabilidades condicionales.

2. Probabilidad clásica versus cuántica

CP fue formalizada matemáticamente por Kolmogorov (1933) Este es el cálculo de medidas de probabilidad, donde un peso no negativo$p(A)$se asigna a cualquier evento $A$. La principal propiedad de CP es su aditividad: si dos eventos $O_{1},O_{2}$son disjuntos, entonces la probabilidad de disyunción de estos eventos es igual a la suma de probabilidades:

$P(O_{1}\lor O_{2})=P(O_{1})+(O_{2})$

QP es el cálculo de amplitudes complejas o, en el formalismo abstracto, vectores complejos. Así, en lugar de operaciones sobre medidas de probabilidad, se opera con vectores. Podemos decir que QP es un modelo vectorial de razonamiento probabilístico. Cada amplitud compleja $\psi$ da la probabilidad por la regla de Born: La probabilidad se obtiene como el cuadrado del valor absoluto de la amplitud compleja.

${\displaystyle P=|\psi |^{2}}$

(para la formalización del espacio de Hilbert, consulte la Sección 3.2, fórmula (7)). Al operar con amplitudes de probabilidad complejas, en lugar de la operación directa con probabilidades, se pueden violar las leyes básicas de CP.

En CP, la fórmula de probabilidad total (FTP) se obtiene usando la aditividad de la probabilidad y la fórmula de Bayes, la definición de probabilidad condicional, $P(O_{2}|O_{1})={\tfrac {P(O_{2})\cap (O_{1})}{PO_{1}}}$, $P(O_{1})>0$

Considere el par, y , de variables aleatorias clásicas discretas. Entonces

$P(B=\beta )=\sum _{\alpha }P(A=\alpha )P(B=\beta |A=\alpha )$

Así, en CP la $B$-La distribución de probabilidad se puede calcular a partir de la $A$-probabilidad y las probabilidades condicionales

$P(B=\beta |A=\alpha )$

En QP, el FTP clásico es perturbado por el término de interferencia (Khrennikov, 2010); para observables cuánticos dicotómicos $A$ y $B$Del tipo von Neumann, es decir, dado por operadores hermitianos ${\hat {A}}$ y ${\hat {B}}$, la versión cuántica de FTP tiene la forma:

$P(B=\beta )=\sum _{\alpha }P(A=\alpha )P(B=\beta |A=\alpha )+2\sum _{\alpha _{1}<\alpha _{2}}\cos \theta _{\alpha _{1}\alpha _{2}}{\sqrt {P(A=\alpha _{1})P(B=\beta |A=\alpha _{1})}}P(A=\alpha _{2})P(B=\beta |a=\alpha _{2})$

$(1)$

$+2\sum _{\alpha _{1}<\alpha _{2}}\cos \theta _{\alpha _{1}\alpha _{2}}{\sqrt {P(A=\alpha _{1})P(B=\beta |A=\alpha _{1})}}P(A=\alpha _{2})P(B=\beta |a=\alpha _{2})$

$(2)$

Si el término de interferencia7 es positivo, entonces el cálculo QP generaría una probabilidad mayor que su contraparte CP dada por el FTP clásico (2). En particular, esta amplificación de probabilidad es la base de la supremacía de la computación cuántica.

Hay una gran cantidad de datos estadísticos de la psicología cognitiva, la toma de decisiones, la biología molecular, la genética y la epigenética que demuestran que los biosistemas, desde las proteínas y las células (Asano et al., 2015b) hasta los humanos (Khrennikov, 2010, Busemeyer y Bruza, 2012) utilizan esta amplificación y operar con actualizaciones que no sean de CP. Continuamos nuestra presentación con tales ejemplos.

3. Instrumentos cuánticos

3.1. Algunas palabras sobre el formalismo cuántico

Denotamos por ${\textstyle {\mathcal {H}}}$ un espacio complejo de Hilbert. Por simplicidad, asumimos que es de dimensión finita. Estados puros de un sistema $S$están dados por vectores normalizados de ${\textstyle {\mathcal {H}}}$ y estados mixtos por operadores de densidad (operadores semidefinidos positivos con traza unitaria). El espacio de los operadores de densidad se denota por $S$ (${\textstyle {\mathcal {H}}}$). El espacio de todos los operadores lineales en ${\textstyle {\mathcal {H}}}$ se denota con el símbolo ${\textstyle {\mathcal {L}}({\mathcal {H}})}$ . A su vez, este es un espacio lineal. Además, ${\textstyle {\mathcal {L}}({\mathcal {H}})}$ es el espacio complejo de Hilbert con el producto escalar,${\textstyle <A|B>=TrA^{*}B}$. Consideramos operadores lineales actuando en ${\textstyle {\mathcal {L}}({\mathcal {H}})}$. Se llaman superoperadores.

La dinámica del estado puro de un sistema cuántico aislado se describe mediante la ecuación de Schrödinger:

$i{\tfrac {d}{dt}}\psi (t)={\widehat {H}}\psi (t)(t),\psi (0)=\psi _{0}$

$(3)$

dónde ${\textstyle {\hat {\mathcal {H}}}}$  es el hamiltoniano del sistema. Esta ecuación implica que el estado puro $\psi (t)$ evoluciona unitariamente $\psi (t)={\hat {U}}(t)\psi _{0}$, donde  ${\hat {U}}(t)=e^{-it{\hat {\mathcal {H}}}}$ Es un grupo paramétrico de operadores unitarios. ,${\hat {U}}(t):{\mathcal {H}}\rightarrow {\mathcal {H}}$ . En física cuántica, hamiltoniano  ${\textstyle {\hat {\mathcal {H}}}}$ está asociado con la energía observable. La misma interpretación se utiliza en biofísica cuántica (Arndt et al., 2009). Sin embargo, en nuestro modelo cuántico que describe el procesamiento de información en biosistemas, el operador ${\textstyle {\hat {\mathcal {H}}}}$ no tiene acoplamiento directo con la energía física. Este es el generador de evolución que describe las interacciones de información.

La dinámica de Schrödinger para un estado puro implica que la dinámica de un estado mixto (representado por un operador de densidad) se describe mediante la ecuación de von Neumann:

${\frac {d{\hat {\rho }}}{dt}}(t)=-i[{\hat {\mathcal {H}}},{\hat {\rho }}(t)],{\hat {\rho }}(0)={\hat {\rho }}_{0}$

$(4)$

3.2. Formalismo de Von Neumann para observables cuánticos

En el formalismo cuántico original (Von Neumann, 1955), físico observable $A$ está representado por un operador hermitiano ${\hat {A}}$ .Consideramos solo operadores con espectros discretos :${\hat {A}}=\sum _{x}x{\hat {E}}^{A}(x)$dónde ${\hat {E}}^{A}(x)$ es el proyector sobre el subespacio de ${\textstyle {\mathcal {H}}}$ correspondiente al valor propio ${\textstyle x}$. Supongamos que el estado del sistema se representa matemáticamente mediante un operador de densidad ${\textstyle \rho }$. Entonces la probabilidad de obtener la respuestar ${\textstyle x}$ viene dada por la regla de Born

${\textstyle Pr\{A=x||\rho \}=Tr[{\widehat {E}}^{A}(x)\rho ]=Tr[{\widehat {E}}^{A}(x)\rho {\widehat {E}}^{A}(x)]}$

$(5)$

y de acuerdo con el postulado de proyección, el estado posterior a la medición se obtiene a través de la transformación de estado:

${\textstyle \rho \rightarrow \rho _{x}={\frac {{\widehat {E}}^{A}(x)\rho {\widehat {E}}^{A}(x)}{Tr{\widehat {E}}^{A}(x)\rho {\widehat {E}}^{A}(x)}}}$

$(6)$

Para comodidad del lector, presentamos estas fórmulas para un estado inicial puro ${\textstyle \psi \in {\mathcal {H}}}$. La regla de Born tiene la forma:

${\textstyle Pr\{A=x||\rho \}=||{\widehat {E}}^{A}(x)\psi ||^{2}=<\psi \mid {\widehat {E}}^{A}(x)\psi >}$

$(7)$

La transformación de estado viene dada por el postulado de proyección:

${\textstyle \psi \rightarrow \psi _{x}={\widehat {E}}^{A}(x)\psi /\parallel {\widehat {E}}^{A}(x)\psi \parallel }$

$(8)$

Aquí el operador observable ${\hat {A}}$ (su descomposición espectral) determina de forma única las transformaciones del estado de retroalimentación${\textstyle {\mathcal {\Im }}_{A}(x)}$ para resultados ${\textstyle x}$

${\textstyle \rho \rightarrow \Im _{A}(x)\rho ={\widehat {E}}^{A}(x)\rho {\widehat {E}}^{A}(x)}$

$(9)$

El mapa ${\textstyle \rho \rightarrow \Im _{A}(x)}$ dada por (9) es el ejemplo más simple (pero muy importante) de instrumento cuántico.

3.3. Actualización de estado no proyectivo: instrumentos atómicos

En general, las propiedades estadísticas de cualquier medida se caracterizan por

1. la distribución de probabilidad de salida ${\textstyle Pr\{{\text{x}}=x\parallel \rho \}}$, la distribución de probabilidad de la salida ${\textstyle x}$ de la medida en el estado de entrada ${\textstyle \rho }$;
2. la reducción del estado cuántico ${\textstyle \rho \rightarrow \rho _{(X=x)}}$,el cambio de estado desde el estado de entrada ${\textstyle \rho }$ al estado de salida ${\textstyle \rho \rightarrow \rho _{(X=x)}}$condicionado al resultado ${\textstyle {\text{X}}=x}$ de la medida

En la formulación de von Neumann, las propiedades estadísticas de cualquier medida de un observable están determinadas únicamente por la regla de Born (5) y el postulado de proyección (6), y están representadas por el mapa (9), un instrumento de tipo von Neumann. Sin embargo, la formulación de von Neumann no refleja el hecho de que el mismo $A$ representado por el operador hermitiano ${\hat {A}}$ en ${\textstyle {\mathcal {H}}}$ puede medirse de muchas maneras.8 Formalmente, tales esquemas de medición están representados por instrumentos cuánticos.

Ahora, consideramos los instrumentos cuánticos más simples del tipo no von Neumann, conocidos como instrumentos atómicos. Comenzamos recordando la noción de POVM (medida valorada por el operador de probabilidad); restringimos las consideraciones a POVM con un dominio de definición discreto ${\textstyle X=\{x_{1}....,x_{N}.....\}}$. POVMes un mapa ${\textstyle x\rightarrow {\hat {D}}(x)}$ tal que para cada ${\textstyle x\in X}$,${\hat {D}}(x)$es un operador hermitiano contractivo positivo (llamado efecto) (es decir,,${\textstyle {\hat {D}}(x)^{*}={\hat {D}}(x),0\leq \langle \psi |{\hat {D}}(x)\psi \rangle \leq 1}$ o cualquier ${\textstyle \psi \in {\mathcal {H}}}$), y la condición de normalización

${\textstyle \sum _{x}{\hat {D}}(x)=I}$

sostiene, donde ${\textstyle I}$ es el operador de la unidad. Se supone que para cualquier medida, la distribución de probabilidad de salida ${\textstyle Pr\{{\text{x}}=x||\rho \}}$ es dado por

${\textstyle Pr\{{\text{x}}=x||\rho \}=Tr[{\hat {D}}(x)\rho ]}$

$(10)$

dónde ${\textstyle {\hat {D}}(x)}$  es un POVM. Para instrumentos atómicos, se supone que los efectos se representan concretamente en la forma

${\textstyle {\hat {D}}(x)={\hat {V}}(x)^{*}{\hat {V}}(x)}$

$(11)$

dónde ${\textstyle {V}(x)}$Es un operador lineal en ( ${\textstyle {\mathcal {H}}}$.Por lo tanto, la condición de normalización tiene la forma ${\textstyle \sum _{x}V(x)^{*}V(x)=I}$.9 La regla de Born se puede escribir de manera similar a (5):

${\textstyle Pr\{{\text{x}}=x||\rho \}=Tr[{V}(x)\rho {V}^{*}(x)]}$

$(12)$

Se supone que la transformación del estado posterior a la medición se basa en el mapa:

*

${\textstyle \rho \rightarrow {\mathcal {L_{A}(x)\rho =V(X)\rho V^{*}(x)}}}$

$(13)$

por lo que la reducción del estado cuántico viene dada por

*

${\textstyle \rho \rightarrow \rho _{({\text{x}}=x)}={\frac {{\mathcal {L}}_{A}(x)\rho }{Tr[{\mathcal {L}}_{A}(x)\rho ]}}}$

$(14)$

El mapa $x\rightarrow {\mathcal {L_{A}(x)}}$ dada por (13) es un instrumento cuántico atómico. Observamos que la regla de Born (12) se puede escribir en la forma

*

${\textstyle Pr\{{\text{x}}=x||\rho \}=Tr[\Im _{A}(x)\rho ]}$

$(15)$f

Dejar ${\hat {A}}$ ser un operador hermitiano en ${\textstyle {\mathcal {H}}}$. Considere un POVM ${\textstyle {\hat {D}}={\biggl (}{\hat {D}}^{A}(x){\Biggr )}}$ con el dominio de definición dado por el espectro de ${\hat {A}}$. Este POVM representa una medida de observable $A$ si se cumple la regla de Born:

${\textstyle Pr\{{\text{A}}=x||\rho \}=Tr[{\widehat {D}}^{A}(x)\rho ]=Tr[{\widehat {E}}^{A}(x)\rho ]}$

$(16)$

Por lo tanto, en principio, las probabilidades de los resultados todavía están codificadas en la descomposición espectral del operador ${\hat {A}}$O en otras palabras operadores ${\textstyle {\biggl (}{\hat {D}}^{A}(x){\Biggr )}}$ deben seleccionarse de tal manera que generen las probabilidades correspondientes a la descomposición espectral de la representación simbólica ${\hat {A}}$ de observables $A$,es decir.,${\textstyle {\biggl (}{\hat {D}}^{A}(x){\Biggr )}}$ está determinada únicamente por ${\hat {A}}$ como ${\textstyle {\hat {D}}^{A}(x)={\hat {E}}^{A}(x)}$. Podemos decir que este operador solo lleva información sobre las probabilidades de los resultados, en contraste con el esquema de von Neumann, el operador ${\hat {A}}$ no codifica la regla de actualización de estado. Para un instrumento atómico, las mediciones del observable $A$ tiene la distribución de probabilidad de salida única según la regla de Born (16), pero tiene muchas reducciones de estado cuántico diferentes dependiendo de la descomposición del efecto ${\textstyle {\hat {D}}(x)={\hat {E}}^{A}(x)=V(x)^{*}V(x)}$ de una manera que

${\textstyle \rho \rightarrow \rho _{({\text{A}}=x)}={\frac {{V}(x)\rho V(x)^{*}}{Tr[{V}(x)\rho V(x)^{*}]}}}$

$(17)$

---

3.4. Teoría general (Davies-Lewis-Ozawa)

Finalmente, formulamos la noción general de instrumento cuántico. Un superoperador actuando en ${\textstyle {\mathcal {L}}({\mathcal {H}})}$ se llama positivo si mapea el conjunto de operadores semidefinidos positivos en sí mismo. Resaltamos que, para cada $x,\Im _{A}(x)$  dado por (13) puede considerarse como un mapa lineal positivo.

Generalmente cualquier mapa $x\rightarrow \Im _{A}(x)$ , donde para cada $x$, el mapa $\Im _{A}(x)$es un superoperador positivo se llama Davies-Lewis (Davies y Lewis, 1970) instrumento cuántico.

Aquí índice ${\textstyle A}$ denota el observable acoplado a este instrumento. Las probabilidades de ${\textstyle A}$-los resultados vienen dados por la regla de Born en forma (15) y la actualización de estado por transformación (14). Sin embargo, Yuen (1987) señaló que la clase de instrumentos de Davies-Lewis es demasiado general para excluir instrumentos físicamente irrealizables. Ozawa (1984) introdujo la importante condición adicional para asegurar que cada instrumento cuántico sea físicamente realizable. Esta es la condición de la positividad completa.

Un superoperador se llama completamente positivo si su extensión natural ${\textstyle \jmath \otimes I}$ al producto tensorial ${\textstyle {\mathcal {L}}({\mathcal {H}})\otimes {\mathcal {L}}({\mathcal {H}})={\mathcal {L}}({\mathcal {H}}\otimes {\mathcal {H}})}$ es de nuevo un superoperador positivo en ${\textstyle {\mathcal {L}}({\mathcal {H}})\otimes {\mathcal {L}}({\mathcal {H}})}$. Un mapa $x\rightarrow \Im _{A}(x)$ , donde para cada ${\textstyle x}$,el mapa $\Im _{A}(x)$es un superoperador completamente positivo se llama Davies-Lewis-Ozawa (Davies y Lewis 1970, Ozawa, 1984instrumento cuántico o simplemente instrumento cuántico. Como veremos en la Sección 4, la positividad completa es condición suficiente para que un instrumento sea físicamente realizable. Por otro lado, la necesidad se deriva de la siguiente manera (Ozawa, 2004)

cada observable ${\textstyle A}$ de un sistema ${\textstyle S}$ se identifica con el observable ${\textstyle A\otimes I}$de un sistema ${\textstyle S+S'}$con cualquier sistema ${\textstyle S'}$ Externo a ${\textstyle S}$ .10

Entonces, cada instrumento físicamente realizable  $\Im _{A}$ medición ${\textstyle A}$ debe identificarse con el instrumento ${\textstyle \Im _{A}{_{\otimes }}_{I}}$medición ${\textstyle A{\otimes }I}$ tal que${\textstyle \Im _{A}{_{\otimes }}_{I}(x)=\Im _{A}(x)\otimes I}$. Esto implica que ${\textstyle \Im _{A}(x)\otimes I}$ es de nuevo un superoperador positivo, por lo que $\Im _{A}(x)$ Es completamente positivo.

Del mismo modo, cualquier instrumento físicamente realizable $\Im _{A}(x)$ sistema de medición ${\textstyle S}$ debe tener su instrumento extendido ${\textstyle \Im _{A}(x)\otimes I}$ sistema de medición ${\textstyle S+S'}$ para cualquier sistema externo ${\textstyle S'}$.Esto se cumple sólo si $\Im _{A}(x)$es completamente positivo. Así, la positividad completa es una condición necesaria para $\Im _{A}$para describir un instrumento físicamente realizable.

4. Instrumentos cuánticos del esquema de medidas indirectas.

El modelo básico para la construcción de instrumentos cuánticos se basa en el esquema de medidas indirectas. Este esquema formaliza la siguiente situación: los resultados de la medición se generan a través de la interacción de un sistema $S$ con un aparato de medida $M$ .Este aparato consiste en un dispositivo físico complejo que interactúa con $S$ y un puntero que muestra el resultado de la medición, digamos girar hacia arriba o hacia abajo. Un observador solo puede ver las salidas del puntero y asocia estas salidas con los valores del observable.$A$ para el sistema $S$.Así, el esquema de medición indirecta implica:

1. los estados del sistemas $S$ y el aparato $M$
2. El operador $U$ representando la dinámica de interacción para el sistema $S+M$
3. el metro observable $M_{A}$ dando salidas del puntero del aparato $M$.

Un modelo de medición indirecta, introducido en Ozawa (1984) como un "proceso de medición (general)", es un cuádruple

$(H,\sigma ,U,M_{A})$

que consta de un espacio de Hilbert ${\mathcal {H}}$ ,un operador de densidad $\sigma \in S({\mathcal {H}})$, Un operador unitario  $U$sobre el producto tensorial de los espacios de estado de  $S$ y $M,U:{\mathcal {H}}\otimes {\mathcal {H}}\rightarrow {\mathcal {H}}\otimes {\mathcal {H}}$y un operador hermitiano $M_{A}$ on ${\mathcal {H}}$ . Por este modelo de medida, el espacio de Hilbert ${\mathcal {H}}$describe los estados del aparato $M$, El operador unitario $U$ describe la evolución temporal del sistema compuesto $S+M$, El operador de densidad $\sigma$ describe el estado inicial del aparato $M$ , y el operador hermitiano $M_{A}$ describe el metro observable del aparato $M$. Entonces, la distribución de probabilidad de salida. $Pr\{A=x\|\sigma \}$en el estado del sistema $\sigma \in S({\mathcal {H}})$ es dado por

$Pr\{A=x\|\rho \}=Tr[{\Bigl (}I\otimes E^{M}{^{_{A}}(x){\Bigr )}}U(\rho \otimes \sigma )U^{*}]$

$(18)$

dónde $E^{M_{A}}(x)$ es la proyección espectral de $M_{A}$ para el valor propio $x$.

El cambio de estado $\sigma$ del sistema $S$ causado por la medición para el resultado $A=x$ se representa con la ayuda del mapa $\Im _{A}(x)$en el espacio de operadores de densidad definidos como

${\mathcal {P}}_{A}(x)\rho =Tr_{\mathcal {H}}[{\Bigl (}I\otimes E^{M}{^{_{A}}(x){\Bigr )}}U(\rho \otimes \sigma )U^{*}]$

$(19)$

dónde $Tr_{\mathcal {H}}$es la traza parcial sobre ${\mathcal {H}}$ . Entonces, el mapa $x\rightarrow \Im _{A}(x)$ resultar ser un instrumento cuántico. Así, las propiedades estadísticas de la medida realizada por cualquier modelo de medida indirecta $(H,\sigma ,U,M_{A})$se describe mediante una medida cuántica. Resaltamos que, a la inversa, cualquier instrumento cuántico puede representarse mediante el modelo de medición indirecta (Ozawa, 1984).Así, los instrumentos cuánticos caracterizan matemáticamente las propiedades estadísticas de todas las medidas cuánticas físicamente realizables.

5. Modelado del proceso de sensación-percepción dentro del esquema de medición indirecta

H. von Helmholtz estableció los fundamentos de la teoría de la inferencia inconsciente para la formación de impresiones visuales en el siglo XIX. Aunque von Helmholtz estudió principalmente la sensación-percepción visual, también aplicó su teoría a otros sentidos hasta culminar en la teoría de la inferencia del inconsciente social. Por von Helmholtz aquí hay dos etapas del proceso cognitivo, y discriminan entre sensación y percepción de la siguiente manera:

• La sensación es una señal que el cerebro interpreta como un sonido o una imagen visual, etc.
• La percepción es algo que debe interpretarse como una preferencia o atención selectiva, etc.

En el esquema de medición indirecta, las sensaciones representan los estados del sistema de sensaciones del ser humano y el sistema de percepción desempeña el papel del aparato de medición. El operador unitario describe el proceso de interacción entre los estados de sensación y percepción. Este modelado cuántico del proceso de sensación-percepción se presentó en papel (Khrennikov, 2015)con aplicación a la percepción biestable y datos experimentales del artículo (Asano et al., 2014).

6. Modelado de efectos cognitivos

En las ciencias cognitivas y sociales, el siguiente grupo de opiniones se conoce como el ejemplo básico del efecto de orden. Este es el grupo de opinión Clinton-Gore (Moore, 2002). En este experimento, a los ciudadanos estadounidenses se les hizo una pregunta a la vez, por ejemplo,

$A=$ "¿Es Bill Clinton honesto y confiable?"

$B=$ "¿Es Al Gore honesto y confiable?"

Se calcularon dos distribuciones de probabilidad secuenciales sobre la base de los datos estadísticos experimentales, $p_{A,B}$ y $p_{B,A}$ (primera pregunta $A$ y luego pregunta $B$ y viceversa).

6.1. Efecto de orden para interrogatorio secuencial

Los datos estadísticos de este experimento demostraron el efecto QOE del orden de las preguntas, la dependencia de la distribución de probabilidad conjunta secuencial para las respuestas a las preguntas en su orden. $p_{(A,B)}\neq p_{(B,A)}$. Observamos que en el modelo CP estas distribuciones de probabilidad coinciden:

$p_{A,B}(\alpha ,\beta )=P(\omega \in \Omega :A(\omega )=\alpha ,B(\omega )=\beta )=p_{A,B}(\beta ,\alpha )$

dónde $\Omega$ es un espacio muestral $P$ y  es una medida de probabilidad.

QOE estimula la aplicación del cálculo QP a la cognición, ver artículo (Wang y Busemeyer, 2013).Los autores de este artículo enfatizaron que la característica no conmutativa de las probabilidades conjuntas se puede modelar mediante el uso de la no conmutatividad de observables cuánticos incompatibles.  $A,B$ representado por operadores hermitianos ${\widehat {A}},{\widehat {B}}$ . Observable  $A$ representa la pregunta de Clinton y observable $B$ representa la pregunta de Gore. En este modelo, QOE es idéntica incompatibilidad-no conmutatividad de observables:

$[{\widehat {A}},{\widehat {B}}]\neq 0$

6.2. Efecto de replicabilidad de respuestas para preguntas secuenciales

El enfoque basado en la identificación del efecto de orden con representación no conmutativa de preguntas(Wang and Busemeyer, 2013) fue criticado en papel (Khrennikov et al., 2014). Para discutir este artículo, recordamos la noción de replicabilidad de la respuesta. Supongamos que a una persona, digamos John, se le hace una pregunta $A$ y supongamos que él responde, por ejemplo, "sí". Si inmediatamente después de esto, se le vuelve a hacer la misma pregunta, entonces responde "sí" con probabilidad uno. A esta propiedad la llamamos $A-A$ replicabilidad de la respuesta. En la física cuántica,  $A-A$ la replicabilidad de la respuesta se expresa mediante el postulado de proyección. La encuesta de opinión de Clinton-Gore, así como los experimentos típicos de toma de decisiones, satisfacen $A-A$replicabilidad de la respuesta. La toma de decisiones también tiene otra característica:  $A-A$ replicabilidad de la respuesta. Supongamos que después de responder a la $A$-pregunta con la respuesta "sí", a John se le hace otra pregunta $B$. Él respondió con alguna respuesta. Y luego se le pregunta $A$de nuevo. En el grupo de opinión social antes mencionado, John repite su respuesta original a $A$,“sí” (con probabilidad uno).

Este fenómeno de comportamiento que llamamos $A-B-A$ replicabilidad de la respuesta. Combinación de $A-A$ con $A-B-A$ y $B-A-B$la replicabilidad de la respuesta se denomina efecto de replicabilidad de la respuesta RRE.

6.3.“QOE+RRE”: descrito por instrumentos cuánticos de tipo no proyectivo

En papel (Khrennikov et al., 2014), se demostró que usando el cálculo de von Neumann es imposible combinar RRE con QOE. Para generar QOE, operadores hermitianos ${\widehat {A}},{\widehat {B}}$ Debe ser no conmutativo, pero este último destruye$A-B-A$ replicabilidad de la respuesta de $A$. Este fue un resultado bastante inesperado. Incluso dio la impresión de que, aunque los efectos cognitivos básicos pueden modelarse cuánticamente por separado, sus combinaciones no pueden describirse mediante el formalismo cuántico.

Sin embargo, recientemente se demostró que la teoría de los instrumentos cuánticos proporciona una solución simple de la combinación de los efectos QOE y RRE, ver Ozawa y Khrennikov (2020a) para la construcción de dichos instrumentos. Estos instrumentos son de tipo no proyectivo. Así, la esencia de QOE no está en la estructura de los observables, sino en la estructura de la transformación de estado generada por la retroalimentación de las medidas. QOE no se trata de la medición conjunta y la incompatibilidad (no conmutatividad) de los observables, sino de la medición secuencial de los observables y la actualización secuencial del estado (mental). Instrumentos cuánticos que se utilizan en Ozawa y Khrennikov (2020a) para combinar QOE y RRE corresponden a la medición de observables representados por operadores de conmutación ${\widehat {A}},{\widehat {B}}$.Además, es posible demostrar que (bajo restricción matemática natural) QOE y RRE pueden modelarse conjuntamente solo con la ayuda de instrumentos cuánticos para conmutar observables.

6.4. Realismo mental

Desde el comienzo de la mecánica cuántica, la no conmutatividad de los operadores. ${\widehat {A}},{\widehat {B}}$ representando observables $A,B$ fue considerada como la representación matemática de su incompatibilidad. En términos filosóficos, esta situación se trata como imposibilidad de la descripción realista. En la ciencia cognitiva, esto significa que existen estados mentales tales que un individuo no puede asignar los valores definidos a ambos observables (por ejemplo, preguntas). La descripción matemática de QOE con observables representados por operadores no conmutativos (en el esquema de von Neumann) en Wang y Busemeyer(2013) y Wang et al. (2014) dio la impresión de que este efecto implica el rechazo del realismo mental. El resultado deOzawa y Khrennikov (2020a) demuestra que, a pesar de QOE experimentalmente bien documentado, el realismo mental no necesita ser rechazado. QOE se puede modelar dentro de la imagen realista dada matemáticamente por la distribución de probabilidad conjunta de observables $A$ y $B$,pero con la acción no conmutativa de los instrumentos cuánticos actualizando el estado mental:

$[{\mathcal {J_{A}(x)}},{\mathcal {J_{B}(x)}}]={\mathcal {J_{A}(x)}}{\mathcal {J_{B}(x)}}-{\mathcal {J_{B}(x)}},{\mathcal {J_{A}(x)}}\neq 0$

$(20)$

Este es un buen lugar para comentar que si, para algún estado $\rho ,[\Im _{A}(x),\Im _{B}(x)]\rho =0$, entonces QOE desaparece, incluso si $[\Im _{A}(x),\Im _{B}(x)]\neq 0$.Esto puede considerarse como la formulación correcta de la declaración de Wang-Bussemeyer sobre la conexión de QOE con la no conmutatividad. En lugar de la no conmutatividad de los operadores  ${\widehat {A}}$ y  ${\widehat {B}}$ representando simbólicamente observables cuánticos, uno tiene que hablar de no conmutatividad de los instrumentos cuánticos correspondientes.

---

7. Genética: interferencia en el metabolismo de glucosa/lactosa

En papel (Asano et al., 2012a),se desarrolló un modelo de tipo cuántico que describe la regulación génica del metabolismo de la glucosa/lactosa en la bacteria Escherichia coli.11 Hay varios tipos de E. coli caracterizados por el sistema metabólico. Se demostró que el tipo concreto de E. coli puede ser descrito por los operadores lineales bien determinados; encontramos las cantidades de operadores invariantes que caracterizan cada tipo. Tales cantidades de operadores invariantes se pueden calcular a partir de los datos estadísticos obtenidos. Entonces, la representación de tipo cuántico se reconstruyó a partir de datos experimentales.

Consideremos un sistema de eventos $\{Q_{+},Q_{-}\}:Q_{+}$ significa el evento en que E. coli activa su operón de lactosa, es decir, el evento en que se produce -galactosidasa a través de la transcripción del ARNm de un gen en el operón de lactosa; $Q_{-}$significa el evento de que E. coli no active su operón de lactosa.

Este sistema de eventos corresponde a una activación observable que es matemáticamente representada por un instrumento cuántico $\Im _{Q}$. Considere ahora otro sistema de eventos $\{D_{L},D_{G}\}$ dónde $D_{L}$significa el evento de que una bacteria E. coli detecta una molécula de lactosa en el entorno circundante de la célula, significa $D_{G}$ detección de una molécula de glucosa. Este sistema de eventos corresponde a la detección observable $D$ que está representado por un instrumento cuántico$\Im _{D}$.

En este modelo, la interacción-reacción de la bacteria con el entorno de glucosa/lactosa se describe como una acción secuencial de dos instrumentos cuánticos, primero la detección y luego la activación. Como se mostró en Asano et al.(2012a), para cada tipo concreto de bacteria E. coli, estos instrumentos cuánticos pueden reconstruirse a partir de los datos experimentales; Asano et al. (2012a),la reconstrucción se realizó para el tipo W3110 de la bacteria E. coli. El FTP clásico con observables  $A=D$ and $B=Q$se viola, el término de interferencia, ver (2), se calculó (Asano et al., 2012a).

8. Sistemas cuánticos abiertos: interacción de un biosistema con su entorno

Como ya se enfatizó, cualquier biosistema $S$ es fundamentalmente abierto. Por lo tanto, la dinámica de su estado debe modelarse a través de una interacción con el entorno circundante. $\varepsilon$. los estados de $S$ y $\varepsilon$ están representados en los espacios de Hilbert ${\mathcal {H}}$ y ${\mathcal {H}}$. el sistema compuesto $S+\varepsilon$ se representa en el producto tensorial espacios de Hilbert. Este sistema se trata como un sistema aislado y, de acuerdo con la teoría cuántica, la dinámica de su estado puro se puede describir mediante la ecuación de Schrödinger:

$i{\tfrac {d}{dt}}\Psi (t)={\widehat {H}}\Psi (t)(t),\Psi (0)=\Psi _{0}$

$(21)$

dónde $\psi (t)$es el estado puro del sistema $S+\varepsilon$ y ${\hat {\mathcal {H}}}$es su hamiltoniano. Esta ecuación implica que el estado puro $\psi (t)$ evoluciona unitariamente: $\psi (t)={\hat {U}}(t)\psi _{0}$. Aquí ${\hat {U}}(t)=e^{-it{\hat {\mathcal {H}}}}$. hamiltoniano (generador de evolución) que describe las interacciones de información tiene la forma ${\hat {\mathcal {H}}}={\hat {\mathcal {H}}}_{s}+{\hat {\mathcal {H}}}_{\varepsilon }+{\mathcal {{\hat {H}}_{S,\varepsilon }}}$, dónde ${\hat {\mathcal {H}}}_{s}$,${\hat {\mathcal {H}}}_{\varepsilon }$son hamiltonianos de los sistemas y  ${\mathcal {{\hat {H}}_{S,\varepsilon }}}$es la interacción hamiltoniana.12 Esta ecuación implica que la evolución del operador de densidad ${\hat {\mathcal {R}}}(t)$ del sistema $S+\varepsilon$ se describe mediante la ecuación de von Neumann:

${\tfrac {d{\widehat {R}}}{dt}}(t)=-i[{\widehat {H}},{\widehat {R}},(t)],{\widehat {R}}(0)={\widehat {R}}_{0}$

$(22)$

Sin embargo, el estado ${\hat {\mathcal {R}}}(t)$ es demasiado complejo para cualquier análisis matemático: el entorno incluye demasiados grados de libertad. Por lo tanto, sólo nos interesa el estado de $S$; su dinámica se obtiene mediante el seguimiento del estado de  $S+\varepsilon$ w.r.t. los grados de libertad de $\varepsilon$ :

${\widehat {\rho }}(t)=Tr_{\mathcal {H}}{\widehat {R}}(t)$

$(23)$

Generalmente esta ecuación, la ecuación maestra cuántica, es matemáticamente muy complicada. En las aplicaciones se utiliza una variedad de aproximaciones.

8.1. Modelo cuántico de Markov: ecuación de Gorini-Kossakowski-Sudarshan-Lindblade

La aproximación más simple de la ecuación maestra cuántica (23) es la dinámica cuántica de Markov dada por la ecuación de Gorini-Kossakowski-Sudarshan-Lindblad (GKSL) (Ingarden et al., 1997) (en física, comúnmente se le llama simplemente la ecuación de Lindblad; esta es la ecuación maestra cuántica más simple):

${\tfrac {d{\widehat {\rho }}}{dt}}(t)=-i[{\widehat {H}},{\widehat {\rho }},(t)]+{\widehat {L}}[{\widehat {\rho }}(t),{\widehat {\rho }}(0)={\widehat {\rho }}_{0}$

$(24)$

donde operador hermitiano (hamiltoniano) ${\widehat {\mathcal {H}}}$ Describe la dinámica interna de $S$ y el superoperador ${\widehat {L}}$, actuando en el espacio de los operadores de densidad, describe una interacción con el entorno $\varepsilon$. Este superoperador a menudo se llama Lindbladian. La ecuación GKSL es una ecuación maestra cuántica para la dinámica markoviana. En este artículo, no tenemos posibilidad de explicar la noción de markovianidad cuántica con más detalle. La ecuación maestra cuántica (23) describe, en general, dinámicas no markovianas.

---

8.2. Funciones biológicas en el marco cuántico de Markov

Pasamos a la dinámica de sistemas abiertos con la ecuación GKSL. En nuestro modelo, hamiltoniano ${\widehat {\mathcal {H}}}$ y Lindbladian ${\widehat {L}}$ representan alguna función biológica especial $F$ (ver Khrennikov et al., 2018)para detalles. Su funcionamiento resulta de la interacción de flujos de información internos y externos. En las Secciones 10, 11.3, $F$ es alguna función psicológica; en el caso más simple $F$ representa una pregunta hecha a  $S$ (digamos que es un ser humano). En la Sección 7, $F$  es la regulación génica del metabolismo de la glucosa/lactosa en la bacteria Escherichia coli. En las Secciones 9, 11.2,  $F$ representa el proceso de mutación epigenética. Función simbólicamente biológica $F$ se representa como un observable cuántico: operador hermitiano ${\widehat {F}}$con la descomposición espectral ${\widehat {F}}=\sum _{x}x{\widehat {E}}^{F}(x)$,dónde $x$ etiqueta las salidas de $F$.La teoría de la dinámica de estado cuántica de Markov describe el proceso de generación de estos resultados.

En el modelo matemático (Asano et al., 2015b, Asano et al., 2017b, Asano et al., 2017a, Asano et al., 2015a, Asano et al., 2012b, Asano et al., 2011, Asano et al. ., 2012a), los resultados de la función biológica $F$ se generan acercándose a un estado estable de la dinámica GKSL:

$\lim _{t\to \infty }{\widehat {\rho }}(t)={\widehat {\rho }}_{steady}$

$(25)$

tal que coincide con la descomposición espectral de ${\widehat {F}}$,es decir.,

${\widehat {\rho }}_{steady}=\sum _{x}p_{x}{\widehat {E}}^{F}(x)$

$(26)$

dónde

$p_{x}\geq \sum _{x}p_{x}=1$

$(26)$

Esto significa que ${\widehat {\rho }}_{steady}$es diagonal en una base ortonormal que consta de vectores propios de ${\widehat {F}}$. Este estado, o más precisamente, esta descomposición del operador de densidad ${\widehat {\rho }}_{steady}$,es la mezcla estadística clásica de los estados básicos de información que determinan esta función biológica. Las probabilidades en la descomposición de estados (26) se interpretan estadísticamente.

Considere un gran conjunto de biosistemas con el estado ${\widehat {\rho }}_{0}$ interactuando con el medio ambiente $\varepsilon$. (Recordemos que matemáticamente la interacción está codificada en el Lindbladian ${\widehat {L}}$) Como resultado de esta interacción, la función biológica $F$ produce salida $x$ con probabilidad $p_{x}$.Observamos que en los términos del operador la probabilidad se expresa como $p_{x}=Tr{\widehat {\rho }}_{steady}{\widehat {E}}^{F}(x)$

Esta interpretación se puede aplicar incluso a un solo biosistema que se encuentra con el mismo entorno muchas veces.

Cabe señalar que el estado límite ${\widehat {\rho }}_{steady}$ expresa la estabilidad con respecto a la influencia del entorno concreto $\varepsilon$.Por supuesto, en el mundo real nunca se alcanzaría el estado límite. La fórmula matemática (25) describe el proceso de estabilización, amortiguación de fluctuaciones. Pero, nunca desaparecerían por completo con el tiempo.

Observamos que un estado estacionario satisface la ecuación GKSL estacionaria:

$i[{\widehat {H}},{\widehat {\rho }}_{steady}]={\widehat {L}}[{\widehat {\rho }}_{steady}]$

$(27)$

También es importante señalar que, en general, un estado estacionario de la ecuación maestra cuántica no es único, depende de la clase de condiciones iniciales.

8.3.Funcionamiento de las funciones biológicas a través de la decoherencia

Para concretar las consideraciones anteriores, consideremos un estado cuántico puro como estado inicial. Supongamos que una función biológica $F$es dicotómica, $F=0,1$, y está representado simbólicamente por el operador hermitiano que es diagonal en base ortonormal $|0\rangle$,$|1\rangle$ .(Consideramos el espacio de estado bidimensional, el espacio qubit). Deje que el estado inicial tenga la forma de superposición

$\psi \rangle =c_{0}|0\rangle +c_{1}|1\rangle$

$(28)$

dónde $c_{j}\in C,|c_{0}|^{2}+||c_{1}|^{2}=1$. La dinámica del maestro cuántico no es una dinámica de estado puro: tarde o temprano (de hecho, muy pronto), esta superposición que representa un estado puro se transferirá a una matriz de densidad que representa un estado mixto. Por lo tanto, desde el principio es útil representar la superposición (28) en términos de una matriz de densidad:

${\widehat {\rho }}_{0}={\begin{vmatrix}|c_{0}|^{2}&c_{0}{\bar {c}}_{1}\\{\bar {c}}_{0}c_{1}&|c_{1}|^{2}\end{vmatrix}}$

$(29)$

La pureza del estado, la superposición, se caracteriza por la presencia de términos distintos de cero fuera de la diagonal.

La superposición codifica la incertidumbre con respecto a la base del estado concreto, en nuestro caso $|0\rangle$,$|1\rangle$.Inicialmente función biológica $F$  estaba en el estado de incertidumbre entre dos opciones $x=0,1$. Esta es una incertidumbre cuántica (como) genuina. Incertidumbre, sobre posibles acciones en el futuro. Por ejemplo, para la función psicológica (Sección 10) $F$representando responder a alguna pregunta, digamos "comprar una propiedad"( $F=1$) y su negacion ( $F=0$) , una persona cuyo estado se describe por superposición (28) no está seguro de actuar con ( $F=1$) o con ( $F=0$) . Así, un estado de tipo superposición describe la incertidumbre individual, es decir, la incertidumbre asociada con el biosistema individual y no con un conjunto de biosistemas; con el solo acto de funcionamiento de $F$ y no con una gran serie de tales actos.

Resolución de la incertidumbre con respecto a ${\widehat {F}}-basis$ se caracteriza por lavar los términos fuera de la diagonal en (29) La dinámica cuántica (24) suprime los términos fuera de la diagonal y, finalmente, se genera una matriz de densidad diagonal que representa un estado estacionario de estos sistemas dinámicos:

${\widehat {\rho }}_{0}={\begin{vmatrix}p_{0}&0\\0&p_{1}\end{vmatrix}}$

$(30)$

Esta es una mezcla estadística clásica. Describe un conjunto de biosistemas; estadísticamente generan salidas $F=\alpha$ con probabilidades $p_{\alpha }$.De la misma manera, la interpretación estadística se puede utilizar para un solo sistema que realiza $F$-funcionando en diferentes instancias de tiempo (para una larga serie de tiempo).

En física cuántica, el proceso de eliminar los elementos fuera de la diagonal en una matriz de densidad se conoce como proceso de decoherencia. Así, el modelo descrito de puede llamarse funcionamiento de la función biológica a través de la decoherencia.

8.4.Linealidad de la representación cuántica: aceleración exponencial del funcionamiento biológico

El modelado de tipo cuántico no afirma que los biosistemas sean fundamentalmente cuánticos. Una imagen más natural es que son sistemas biofísicos clásicos complejos y el modelo cuántico proporciona la representación de información de procesos biofísicos clásicos, en genes, proteínas, células, cerebros. Una de las ventajas de esta representación es su linealidad. El espacio de estado cuántico es un espacio de Hilbert complejo y las ecuaciones dinámicas son ecuaciones diferenciales lineales. Para espacios de estado de dimensión finita, estas son solo ecuaciones diferenciales ordinarias con coeficientes complejos (por lo tanto, el lector no debe temer nombres tan patéticos como ecuaciones de Schrödinger, von Neumann o Gorini-Kossakowski-Sudarshan-Lindblad). La dinámica biofísica clásica más allá de la representación de la información cuántica suele ser no lineal y muy complicada. El uso de la representación del espacio lineal simplifica la estructura de procesamiento. Hay dos puntos de vista sobre esta simplificación, externa e interna. El primero es la simplificación del modelado matemático, es decir, la simplificación del estudio de bioprocesos (por nosotros, observadores externos). El segundo es más delicado e interesante. Ya hemos señalado una especialidad importante de las aplicaciones de la teoría cuántica a la biología. Aquí, los sistemas pueden realizar autoobservaciones. Entonces, en el proceso de evolución, digamos que una célula puede "aprender" a través de tales autoobservaciones que es computacionalmente rentable usar la representación lineal de tipo cuántico. Y ahora, llegamos a la principal ventaja de la linealidad.

La dinámica lineal acelera exponencialmente el procesamiento de la información. Las soluciones de la ecuación GKSL se pueden representar en la forma ${\widehat {\rho }}(t)=e^{t{\widehat {\Gamma }}}{\widehat {\rho }}$, dónde ${\widehat {\Gamma }}$ es el superoperador dado por el lado derecho de la ecuación GKSL. En el caso de dimensión finita, la dinámica de decoherencia se expresa a través de factores de la forma $e^{t{(ia-b)}}$,dónde $b>0$. Dichos factores están disminuyendo exponencialmente. La realización lineal de tipo cuántico de las funciones biológicas es exponencialmente rápida en comparación con la dinámica clásica no lineal.

El uso de la representación de información cuántica significa que, en general, grandes grupos de estados biofísicos clásicos están codificados por unos pocos estados cuánticos. Significa una gran compresión de información. También implica un aumento de la estabilidad en el procesamiento de estado. La dinámica clásica no lineal ruidosa se asigna a la dinámica impulsada por una ecuación cuántica lineal (similar) de, digamos, tipo GKSL.

Este último tiene una estructura esencialmente más simple y, a través de la selección de los coeficientes del operador, codifica simbólicamente la interacción dentro del sistema. $S$ y con su entorno circundante $\varepsilon$,  $S$ pueden establecer dinámicas con regímenes de estabilización que conducen a estados estacionarios.

9.Evolución epigenética dentro de la teoría de los sistemas cuánticos abiertos

En papel (Asano et al., 2012b),En el marco de la teoría de los sistemas cuánticos abiertos, se creó un modelo general de la evolución epigenética que unifica los enfoques neodarwiniano y neolamarckiano. El proceso de evolución se representa en forma de dinámica adaptativa dada por la ecuación maestra cuántica (similar a) que describe la dinámica del estado de información del epigenoma en el proceso de interacción con el entorno circundante. Este modelo de evolución epigenética expresa las probabilidades de observaciones que se pueden hacer sobre los epigenomas de las células; este modelo (de tipo cuántico) no proporciona una descripción detallada de los procesos celulares. El enfoque operativo cuántico brinda la posibilidad de describir mediante un modelo todos los tipos conocidos de herencia epigenética celular.

Para dar alguna pista sobre el modelo, consideramos un gen, digamos $g$. este es el sistema $S$ en la Sección 8.1. Interactúa con el entorno que lo rodea.  $\varepsilon$ una célula que contiene este gen y otras células que envían señales a esta célula concreta y a través de ella al gen $g$.Como consecuencia de esta interacción alguna mutación epigenética $\mu$ en el gen $g$ puede pasar. Cambiaría el nivel de la $g$-expresión.

Por el momento, ignoramos que hay otros genes. En este modelo simplificado en exceso, la mutación se puede describir dentro del espacio de estado bidimensional, el espacio de Hilbert complejo ${\mathcal {H}}_{epi}$(espacio qubit). Estados de $g$ sin y con mutación están representados por la base ortogonal $|0\rangle$,$|1\rangle$;estos vectores expresan posibles cambios epigenéticos del tipo fijo $\mu$.

Un estado de información cuántica pura tiene la forma de superposición $|\psi \rangle _{epi}=c_{0}|0\rangle +c_{1}|1\rangle$.

Ahora, pasamos al esquema general de la Sección 8.2 con la función biológica $F$ expresando $\mu$-epimutación en un gen fijo. La dinámica cuántica de Markov (24) resuelve la incertidumbre codificada en superposición $|\psi \rangle _{epi}$ (“modelado de epimutaciones como decoherencia”). La mezcla estadística clásica , ${\rho }_{steady}$ver(30),se acerca. Sus elementos diagonales $p_{0},p_{1}$dar las probabilidades de los eventos: “no $\mu$-epimutación” y “$\mu$-epimutación”. Estas probabilidades se interpretan estadísticamente: en una gran población de células, $M$ células,$M\gg 1$ , el número de celdas con $\mu$-epimutación es $N_{m}\approx p_{1}M$.Esta $\mu$-epimutación en una población celular se estabilizaría completamente al estado estacionario solo en el tiempo infinito. Por lo tanto en realidad hay fluctuaciones (de amplitud decreciente) en cualquier intervalo finito de tiempo.

Finalmente, señalamos la ventaja de la dinámica cuántica de la interacción de los genes con el medio ambiente: la linealidad de la dinámica implica una aceleración exponencial del proceso de evolución epigenética (Sección 8.4).

10. Conexión de procesos electroquímicos en redes neuronales con procesamiento de información cuántica

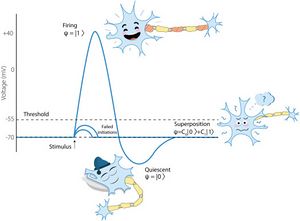
Como se enfatizó en la introducción, los modelos cuánticos son modelos operativos formales que describen el procesamiento de información en biosistemas. (en contraste con los estudios en biología cuántica, la ciencia sobre los procesos físicos cuánticos genuinos en los biosistemas). Sin embargo, es interesante conectar la estructura de procesamiento de información cuántica en un biosistema con procesos físicos y químicos en él. Este es un problema de alta complejidad. Papel (Khrennikov et al., 2018) presenta un intento de proceder en esta dirección para el cerebro humano, el biosistema más complicado (y al mismo tiempo el más interesante para los científicos). En el marco de la teoría cuántica de la información, las redes neuronales del cerebro modelaron el procesamiento de la información. La formalización de la información cuántica de los estados de las redes neuronales se combina con los procesos electroquímicos en el cerebro. El punto clave es la representación de la incertidumbre generada por el potencial de acción de una neurona como una superposición cuántica (similar a) de los estados mentales básicos correspondientes a un código neuronal, vea la Fig. 1 para una ilustración.

Considere el procesamiento de información por una sola neurona; este es el sistema  $S$ (ver Sección 8.2). Su estado de información cuántica correspondiente al código neuronal inactivo y disparando, $0/1$,se puede representar en el complejo bidimensional ${\mathcal {H}}_{neuron}$ espacio de Hilbert (espacio qubit). En un instante concreto de tiempo, el estado de la neurona se puede describir matemáticamente mediante la superposición de dos estados, etiquetados por  $|0\rangle$,$|1\rangle$: $|\psi _{neuron}\rangle =c_{0}|0\rangle +c_{1}|1\rangle$. Se supone que estos estados son ortogonales y normalizados, es decir, $\langle 0|1\rangle =0$ y $\langle \alpha |\alpha \rangle =1$, $\alpha =0,1$. Las coordenadas $c_{0}$ y  $c_{1}$con respecto a la base de disparo en reposo, hay amplitudes complejas que representan potencialidades para la neurona $S$ estar inactivo o disparando. La superposición representa incertidumbre en el potencial de acción, "disparar" o "no disparar". Esta superposición es una representación de información cuántica de la incertidumbre física y electroquímica.

Dejar $F$ ser alguna función psicológica (cognitiva) realizada por esta neurona. (Por supuesto, esto es una simplificación excesiva, considerada, por ejemplo, en el paradigma "neurona abuela"; consulte la Sección 11.3 para el modelado de $F$ basado en una red neuronal). Asumimos que $F=0,1$es dicotómica. Decir $F$ representa algún instinto, por ejemplo, agresión: "ataque" $=1$,"no ataque" $=0$.

Una función psicológica puede representar responder a alguna pregunta (o clase de preguntas), resolver problemas, realizar tareas. Matemáticamente $F$está representado por el operador hermitiano ${\widehat {F}}$  que es diagonal en la base $|0\rangle$,$|1\rangle$. la neurona $S$ interactúa con el entorno electroquímico circundante $\varepsilon$.Esta interacción genera la evolución del estado de la neurona y la realización de la función psicológica. $F$. Modelamos la dinámica con la ecuación maestra cuántica (24). La decoherencia transforma el estado puro $|\psi _{neuron}\rangle$en la mezcla estadística clásica (30), un estado estacionario de esta dinámica. Esta es la resolución de la incertidumbre electroquímica original en el potencial de acción de la neurona.

Los elementos diagonales de ${\widehat {\rho }}_{steady}$dar las probabilidades con la interpretación estadística: en un gran conjunto de neuronas (individualmente) interactuando con el mismo entorno $\varepsilon$ , decir  $M$ neuronas,$M\gg 1$ , el número de neuronas que toman la decisión $F=1$ igual al elemento diagonal $p_{1}$.

También señalamos la ventaja de la dinámica de tipo cuántico de la interacción de una neurona con su entorno: la linealidad de la dinámica implica una aceleración exponencial del proceso de evolución del estado de la neurona hacia una "matriz de decisión" dada por un estado estacionario (Sección 8.4).

11. Biosistemas compuestos

11.1. Enredo de estados de información de biosistemas.

El espacio de estado ${\mathcal {H}}$ del biosistema $S$ compuesto por el subsistemas $S_{j},j=1,2,....n$, es el producto tensorial de los espacios de estado de los subsistemas ${\mathcal {H}}_{j}$ , entonces

*

$\Im =\Im _{1}\otimes ....\otimes \Im _{n}$

$(31)$

La forma más fácil de imaginar este espacio de estados es considerar su representación coordinada con respecto a alguna base construida con bases en ${\mathcal {H}}_{j}$. Para simplificar, considere el caso de los espacios de estado qubit ${\mathcal {H}}_{j}$dejar $|\alpha \rangle$, $|\alpha \rangle =0,1$, ser alguna base ortonormal en${\mathcal {H}}_{j}$,es decir, los elementos de este espacio son combinaciones lineales de la forma $|\psi _{j}\rangle =c_{0}|0\rangle +c_{1}|1\rangle$.(Para ser completamente formal, tenemos que etiquetar los vectores base con el índice $j$, es decir.,$|\alpha \rangle \equiv |\alpha \rangle _{j}$.Pero lo omitiremos.) Entonces vectores$|\alpha _{1}.....\alpha _{n}\rangle \equiv |\alpha _{1}\rangle \otimes ....\otimes |\alpha _{n}\rangle$ formar la base ortonormal en ${\mathcal {H}}$,es decir, cualquier estado  $|{\mathcal {\Psi }}\in {\mathcal {H}}$ se puede representar en la forma

$|\psi \rangle =\sum _{\alpha _{j}=0,1}C_{(}\alpha _{1)}....\alpha _{n}|\alpha _{1}....\alpha _{n}\rangle$

$(32)$

y las coordenadas complejas  $C_{\alpha _{1}.....\alpha _{n}}$ se normalizan: $\sum |C_{\alpha _{1}.....\alpha _{n}}|^{2}=1$. Por ejemplo, si $n=2$, Nosotros podemos considerar el estado

$|\Psi \rangle =(|00\rangle +|11\rangle )/{\sqrt {2}}$

$(33)$

Este es un ejemplo de un estado entrelazado, es decir, un estado que no se puede factorizar en el producto tensorial de los estados de los subsistemas. Un ejemplo de un estado no entrelazado (hasta la normalización) viene dado por

$|00\rangle +|01\rangle +|10\rangle +|11\rangle =(|0\rangle +|1\rangle )\otimes (|1\rangle +|0\rangle )$

Los estados entrelazados son estados básicos para la computación cuántica que explora la inseparabilidad del estado. Actuar sobre un qubit concreto modifica todo el estado. Para un estado separable, al transformar digamos el primer qubit, solo cambiamos el estado del sistema $S_{1}$ .Esta posibilidad de cambiar el estado muy complejo de un sistema compuesto mediante el cambio del estado local de un subsistema se considera como la raíz de la superioridad de la computación cuántica sobre la clásica. Observamos que la dimensión del espacio de estado del producto tensorial es muy grande, es igual a $2^{n}$ para $n$ subsistemas qubit. En la física cuántica, esta posibilidad de manipular con el estado compuesto (que puede tener la gran dimensión) se asocia típicamente con la "no localidad cuántica" y la acción espeluznante a distancia. Pero, incluso en la física cuántica, esta interpretación no local es fuente de debates permanentes. []. En particular, en la serie reciente de artículos [] se demostró que es posible proceder sin referirse a la no localidad cuántica y que la mecánica cuántica puede interpretarse como la teoría física local. El punto de vista local sobre la teoría cuántica es más natural para la aplicación biológica.13 Para los biosistemas, la acción espeluznante a distancia es realmente misteriosa; para los humanos, corresponde a la aceptación de los fenómenos parapsicológicos.

Cómo se puede explicar la generación de transformación de estado del sistema compuesto $S$por "transformación local" de, digamos, el estado de su subsistema $S_{1}$? Aquí, el papel clave lo desempeñan las correlaciones que están codificadas simbólicamente en estados entrelazados. Por ejemplo, considere el sistema compuesto $S=(S_{1},S_{2})$ en el estado $|\Psi \rangle$dada por (33). Considere los observables de tipo proyección $A_{j}$ en $A_{j}$representado por operadores hermitianos ${\widehat {A}}_{j}$ con vectores propios $|0\rangle$,$|1\rangle$ (en espacios qubit ${\mathcal {H}}_{j}$). medida de decir $A_{1}$ con la salida $A_{1}=\alpha$ induce la proyección de estado sobre el vector $|\alpha \alpha \rangle$.

Por lo tanto, la medición de  $A_{2}$ producirá automáticamente la salida $A_{2}=\alpha$. Así, el estado $|\Psi \rangle$codifica las correlaciones exactas para estos dos observables. De la misma manera, el estado

$|\Psi \rangle =(|10\rangle +|01\rangle )/{\sqrt {2}}$

$(34)$

codifica correlaciones$A_{1}=\alpha$, $A_{2}=\alpha$ (modo 2).

Entonces, 'un estado entrelazado proporciona la representación simbólica de las correlaciones entre los estados de los subsistemas de un biosistema compuesto'

La teoría de los sistemas cuánticos abiertos opera con estados mixtos descritos por operadores de densidad. Y antes de pasar al modelado de funciones biológicas para sistemas compuestos, definimos entrelazamiento para estados mixtos. Considere el caso del producto tensorial de dos espacios de Hilbert, es decir, el sistema $S$ Está compuesto de dos subsistemas $S_{1}$ and $S_{2}$. Un estado mixto de$S$ dada por ${\widehat {\rho }}$se llama separable si se puede representar como una combinación convexa de estados del producto ${\widehat {\rho }}=\sum _{k}p_{k}{\widehat {\rho }}_{1k}\otimes {\widehat {\rho }}_{2k}$, dónde ${\widehat {\rho }}ik$, $i=1,2$,son el operador de densidad del subsistema $S_{i}$ de $S$. Los estados no separables se denominan entrelazados. Representan simbólicamente correlaciones entre subsistemas.

La dinámica cuántica describe la evolución de estas correlaciones. En el marco de la dinámica de sistemas abiertos, una función biológica se acerca al estado estacionario a través del proceso de decoherencia. Como se discutió en la Sección 8.3, esta dinámica resuelve la incertidumbre que inicialmente estaba presente en el estado de un biosistema; al mismo tiempo, también elimina las correlaciones: el estado estacionario que es diagonal en la base $\{|\alpha _{1}....\alpha _{2}\rangle \}$es separable (desenmarañado). Sin embargo, en el proceso de evolución del estado, las correlaciones entre subsistemas (entrelazamiento) juegan un papel crucial. Su presencia conduce a transformaciones del estado del sistema compuesto.  $S$ vía “transformaciones locales” de los estados de sus subsistemas. Tal dinámica correlacionada del estado de la información global refleja la consistencia de las transformaciones de los estados de los subsistemas.

Dado que el enfoque cuántico se basa en la representación de la información cuántica de los estados de los sistemas, podemos olvidarnos de la ubicación del espacio físico de los biosistemas y trabajar en el espacio de información proporcionado por el complejo espacio de Hilbert. ${\mathcal {H}}$.En este espacio, podemos introducir la noción de localidad basada en la descomposición del producto tensorial fijo (31). Operaciones en sus componentes${\mathcal {H}}_{j}$podemos llamar local (en espacio de información). Pero inducen una evolución "informativamente no local" del estado del sistema compuesto.

11.2. Enredo de epimutaciones de genes

Ahora, volvemos al modelo presentado en la Sección 9 y consideramos el estado de información del epigenoma de la célula que expresa epimutaciones potenciales del tipo de marcado de cromatina. Deje que el genoma de la célula consista en $m$ genes $g_{1},....,g_{m}$.Para cada gen $g$,considere todas sus epimutaciones posibles y enumérelas: $j_{g}=1,......k_{g}$. El estado de todas las posibles epimutaciones en el gen. $g$ se representa como superposición

$|\psi _{g}\rangle =\sum _{j_{g}}c_{j_{g})}|j_{g}\rangle$

$(35)$

En la situación ideal (las epimutaciones de los genes son independientes), el estado del epigenoma de la célula se describe matemáticamente mediante el producto tensorial de los estados. $|\psi _{g}\rangle$:

$|\psi _{epi}\rangle =|\psi _{g_{1}}\rangle \otimes ....\otimes |\psi _{g_{m}}\rangle$

$(36)$

Sin embargo, en un biosistema vivo, la mayoría de los genes y proteínas están correlacionados formando un gran sistema de red. Por lo tanto, una epimutación afecta a otros genes. En el marco de la información cuántica, esta situación se describe mediante estados entrelazados:

$|\psi _{epi}\rangle =\sum _{j_{g_{1}....{j_{g_{m}}}}}C_{j_{g_{1}....{j_{g_{m}}}}}|j_{g_{1}}...j_{g_{m}}\rangle$

$(37)$

Esta forma de representación de epimutaciones potenciales en el genoma de una célula implica que la epimutación en un gen es consistente con epimutaciones en otros genes. Si el estado está enredado (no factorizado), entonces al actuar, es decir, a través del cambio en el entorno, a un gen, digamos $g_{1}$, e induciendo alguna epimutación en ella, la célula “puede inducir” epimutaciones consistentes en otros genes.

La linealidad de la representación de la información cuántica de los procesos biofísicos en una célula induce la dinámica del estado lineal. Esto hace que la evolución epigenética sea muy rápida; los elementos fuera de la diagonal de la matriz de densidad disminuyen exponencialmente rápidamente. Por lo tanto, nuestro modelo de tipo cuántico justifica la alta velocidad de la evolución epigenética. Si se basara únicamente en la representación biofísica con dinámica de estado no lineal, sería esencialmente más lento.

El modelado basado en la teoría de los sistemas abiertos conduce a la reconsideración de la interrelación entre el punto de vista darwiniano y lamarckiano sobre la evolución. Aquí nos concentramos en epimutaciones, pero de la misma manera podemos modelar mutaciones (Asano et al., 2015b).

11.3. funciones psicologicas

Ahora, pasamos al modelo presentado en la Sección 10. Una red neuronal se modela como un sistema cuántico compuesto; su estado se presenta en el producto tensorial de espacios de estado de una sola neurona. Las funciones del cerebro realizan automediciones modeladas dentro de la teoría de los sistemas cuánticos abiertos. (No hay necesidad de considerar el colapso del estado.) La dinámica del estado de alguna función cerebral (función psicológica) $F$ se describe mediante la ecuación maestra cuántica. Sus estados estacionarios representan mezclas estadísticas clásicas de posibles salidas de $F$ (decisiones). Por lo tanto, a través de la interacción con el entorno electroquímico, $F$(considerado como un sistema abierto) resuelve la incertidumbre que originalmente estaba codificada en estado entrelazado que representa incertidumbres en los potenciales de acción de las neuronas y las correlaciones entre ellos.

El entrelazamiento juega un papel crucial en la generación de consistencia en la dinámica de las neuronas. Como en la Sección 11.1, suponga que la representación de la información cuántica se basa en 0–1 $0-1$ código. Considere una red de $n$ neuronas que interactúan con el entorno electroquímico circundante $\varepsilon$,incluyendo la señalización de otras redes neuronales. El estado de la información viene dado por (32). El enredo codifica correlaciones entre la activación de neuronas individuales. Por ejemplo, el estado (33) está asociado con dos neuronas disparando sincrónicamente y el estado (34) con dos neuronas disparando asincrónicamente.

Salidas de la función psicológica $F$ basados biofísicamente en una red neuronal son el resultado de dinámicas de estado consistentes de neuronas individuales que pertenecen a esta red. Como ya se destacó, la evolución del estado hacia un estado estacionario es muy rápida, como consecuencia de la linealidad de la dinámica del sistema abierto; los elementos fuera de la diagonal de la matriz de densidad disminuyen exponencialmente rápidamente.

12. Observaciones finales

Desde 1990 (Khrennikov, 1999), el modelado de tipo cuántico fuera de la física, especialmente el modelado de la cognición y la toma de decisiones, floreció en todo el mundo. La teoría de la información cuántica (junto con la medición y las teorías de sistemas cuánticos abiertos) es un terreno fértil para las flores de tipo cuántico. La hipótesis básica presentada en este trabajo es que el funcionamiento de los biosistemas se basa en la representación de información cuántica de sus estados. Esta representación es el resultado de la evolución biológica. Este último es considerado como la evolución en el espacio de la información. Entonces, los biosistemas reaccionan no solo a las restricciones materiales o energéticas impuestas por el medio ambiente, sino también a las restricciones de información. En este artículo, las funciones biológicas se consideran como sistemas de información abiertos que interactúan con el entorno de información.

La representación cuántica de la información brinda la posibilidad de procesar superposiciones. Esta forma de procesamiento de la información es ventajosa para ahorrar recursos computacionales: una función biológica $F$ no necesita resolver incertidumbres codificadas en superposiciones y calcular JPD de todas las variables compatibles involucradas en el desempeño de $F$.

Otra característica ventajosa del procesamiento de información de tipo cuántico es su linealidad. La transición de la dinámica no lineal de los estados electroquímicos a la dinámica lineal de tipo cuántico acelera enormemente el procesamiento de estados (para la expresión génica, las epimutaciones y, en general, la toma de decisiones). En este marco, los tomadores de decisiones son genes, proteínas, células, cerebros, sistemas ecológicos.

Las funciones biológicas desarrollaron la capacidad de realizar automediciones, para generar resultados de su funcionamiento. Modelamos esta habilidad en el marco de los sistemas cuánticos abiertos, como toma de decisiones a través de la decoherencia. Hacemos hincapié en que este modelo está libre de la ambigua noción de colapso de la función de onda.

Las correlaciones dentro de una función biológica, así como entre diferentes funciones biológicas y el entorno, se representan linealmente mediante estados cuánticos entrelazados.

Esperamos que este documento sea útil para los biólogos (especialmente los que trabajan en modelos matemáticos) como una introducción al enfoque cuántico para modelar el funcionamiento de los biosistemas. También esperamos que pueda atraer la atención de expertos en teoría cuántica de la información sobre la posibilidad de utilizar su formalismo y metodología en estudios biológicos.

Declaración de interés en competencia

Los autores declaran que no tienen intereses financieros en competencia conocidos ni relaciones personales que pudieran haber parecido influir en el trabajo informado en este documento.

Expresiones de gratitud

Este trabajo fue financiado parcialmente por JSPS, Japón KAKENHI, Nos. 26247016 y 17K19970. MES. reconoce el apoyo de la colaboración IRI-NU, Japón.

Bibliography & references

Masticationpedia is a charity, a not-for-profit organization operating in dentistry medical research,
particularly focusing on the field of the neurophysiology of the masticatory system
 

Home

Introduction

Latest chapter

Ed. Lab

Donate

Contacts