Quantenähnliche Modellierung in der Biologie mit offenen Quantensystemen und Instrumenten
| Title | Quantenähnliche Modellierung in der Biologie mit offenen Quantensystemen und Instrumenten |
| Authors | Irina Basieva · Andrei Khrennikov · Masanao Ozawa |
| Source | Document |
| Date | 2021 |
| Journal | Biosystems |
| DOI | 10.1016/j.biosystems.2020.104328 |
| PUBMED | https://pubmed.ncbi.nlm.nih.gov/33347968/ |
| PDF copy | |
| License | CC BY |
| This resource has been identified as a Free Scientific Resource, this is why Masticationpedia presents it here as a mean of gratitude toward the Authors, with appreciation for their choice of releasing it open to anyone's access | |
This is free scientific content. It has been released with a free license, this is why we can present it here now, for your convenience. Free knowledge, free access to scientific knowledge is a right of yours; it helps Science to grow, it helps you to have access to Science
This content was relased with a 'CC BY' license.
You might perhaps wish to thank the Author/s
Irina Basievaa, Andrei Khrennikova, Masanao Ozawab,c
aLinnaeus University, International Center for Mathematical Modeling in Physics and Cognitive Sciences Växjö, SE-351 95, Sweden
bCollege of Engineering, Chubu University, 1200 Matsumoto-cho, Kasugai 487-8501, Japan
cGraduate School of Informatics, Nagoya University, Chikusa-ku, Nagoya 464-8601, Japan
Abstrait
Nous présentons la nouvelle approche de la modélisation mathématique des processus d'information dans les biosystèmes. Il explore le formalisme mathématique et la méthodologie de la théorie quantique, en particulier la théorie de la mesure quantique. Cette approche est dite de type quantique et doit être distinguée de l'étude des véritables processus physiques quantiques dans les biosystèmes (biophysique quantique, cognition quantique). Il est basé sur la représentation de l'information quantique de l'état du biosystème et la modélisation de sa dynamique dans le cadre de la théorie des systèmes quantiques ouverts. Cet article commence par une présentation conviviale pour les non-physiciens de la théorie de la mesure quantique, de la formulation originale de von Neumann à la théorie moderne des instruments quantiques. Ensuite, ce dernier est appliqué à des modèles de combinaisons d'effets cognitifs et de régulation génique du métabolisme du glucose/lactose chez la bactérie Escherichia coli. La construction la plus générale des instruments quantiques est basée sur le schéma de la mesure indirecte, en ce sens que l'appareil de mesure joue le rôle d'environnement pour un biosystème. L'essence biologique de ce schéma est illustrée par la formalisation quantique de la théorie sensation-perception de Helmholtz. Ensuite, nous passons à la dynamique des systèmes ouverts et considérons l'équation maîtresse quantique, en nous concentrant sur les processus quantiques de Markov. Dans ce cadre, nous modélisons le fonctionnement des fonctions biologiques telles que les fonctions psychologiques et la mutation épigénétique.
Keywords
Mathematical formalism of quantum mechanics, Open quantum systems, Quantum instruments, Quantum Markov dynamics, Gene regulation, Psychological effects,Cognition, Epigenetic mutation, Biological functions
Introduction
Les méthodes mathématiques standard ont été développées à l'origine pour servir la physique classique. L'analyse réelle a servi de base mathématique à la mécanique newtonienne (Newton, 1687)[1] (et plus tard au formalisme hamiltonien) ; la mécanique statistique classique a stimulé l'approche théorique de la mesure de la théorie des probabilités, formalisée dans l'axiomatique de Kolmogorov (Kolmogorov, 1933).[2] Cependant, le comportement des systèmes biologiques diffère essentiellement du comportement des systèmes mécaniques, par exemple des corps rigides, des molécules de gaz ou des fluides. Par conséquent, bien que les «mathématiques classiques» jouent toujours le rôle crucial dans la modélisation biologique, il semble qu'elles ne puissent pas décrire pleinement la riche complexité des biosystèmes et les particularités de leur comportement - par rapport aux systèmes mécaniques. De nouvelles méthodes mathématiques de modélisation des biosystèmes sont en demande.(a,b)
Dans cet article, nous présentons les applications du formalisme mathématique de la mécanique quantique et de sa méthodologie à la modélisation du comportement des biosystèmes. (c) Les dernières années ont été caractérisées par une explosion d'intérêt pour les applications de la théorie quantique en dehors de la physique, en particulier en psychologie cognitive, la prise de décision, le traitement de l'information dans le cerveau, la biologie moléculaire, la génétique et l'épigénétique, et la théorie de l'évolution.4 Nous appelons les modèles correspondants de type quantique. Ils ne sont pas dirigés vers la modélisation au niveau micro des processus physiques quantiques réels dans les biosystèmes, disons dans les cellules ou les cerveaux (cf. avec les applications biologiques de la théorie physique quantique authentique Penrose 1989,[3] Umezawa 1993,[4] Hameroff 1994,[5] Vitiello 1995,[6] Vitiello 2001,[7] Arndt et al., 2009,[8] Bernroider et Summhammer 2012,[9] Bernroider 2017[10]). La modélisation de type quantique fonctionne du point de vue de la théorie quantique en tant que théorie de la mesure. C'est le point de vue original de Bohr qui a conduit à l'interprétation de Copenhague de la mécanique quantique (voir Plotnitsky, 2009[11] pour une présentation détaillée et claire des vues de Bohr). L'une des principales spécialités des biosystèmes est la prise en compte des auto-mesures que les biosystèmes effectuent sur eux-mêmes. Dans notre modélisation, la capacité à effectuer des auto-mesures est considérée comme la caractéristique de base des fonctions biologiques (voir la section 8.2 et l'article de Khrennikov et al., 2018[12]).
Les modèles de type quantique (Khrennikov, 2004b[13]) reflètent les caractéristiques des processus biologiques qui correspondent naturellement au formalisme quantique. Dans une telle modélisation, il est utile d'explorer la théorie de l'information quantique, qui peut être appliquée non seulement au micro-monde des systèmes quantiques. Généralement, les systèmes traitant l'information de manière quantique n'ont pas besoin d'être des systèmes physiques quantiques; en particulier, il peut s'agir de biosystèmes macroscopiques. Étonnamment, la même théorie mathématique peut être appliquée à toutes les échelles biologiques : des protéines, des cellules et des cerveaux aux humains et aux écosystèmes ; on peut parler de biologie de l'information quantique (Asano et al., 2015a[14]).
Dans la modélisation de type quantique, la théorie quantique est considérée comme un calcul pour la prédiction et la transformation des probabilités. Le calcul des probabilités quantiques (QP) (Section 2) diffère essentiellement du calcul classique des probabilités (CP) basé sur l'axiomatique de Kolmogorov (Kolmogorov, 1933[15]). En CP, les états des systèmes aléatoires sont représentés par des mesures de probabilité et les observables par des variables aléatoires ; dans QP, les états de systèmes aléatoires sont représentés par des vecteurs normalisés dans un espace de Hilbert complexe (états purs) ou généralement par des opérateurs de densité (états mixtes)5. Les superpositions représentées par des états purs sont utilisées pour modéliser l'incertitude qui n'est pas encore résolue par une mesure. L'utilisation des superpositions en biologie est illustrée par la Fig. 1 (voir Section 10 et article Khrennikov et al., 2018[12] pour le modèle correspondant). La mise à jour QP résultant d'une observation est basée sur le postulat de projection ou des transformations plus générales d'états quantiques — dans le cadre de la théorie des instruments quantiques (Davies et Lewis, 1970,[16] Davies, 1976,[17] Ozawa 1984,[18] Yuen, 1987,[19] Ozawa 1997,[20] Ozawa, 2004,[21] Okamura et Ozawa, 2016[22]) (Section 3).
Nous soulignons que la modélisation de type quantique élève le rôle de la commodité et de la simplicité de la représentation quantique des états et des observables. (Nous ignorons pragmatiquement le problème de l'interrelation de CP et QP.) En particulier, l'espace d'état quantique a la structure linéaire et les modèles linéaires sont plus simples. La transition de la dynamique non linéaire classique des processus électrochimiques dans les biosystèmes à la dynamique linéaire quantique accélère essentiellement l'évolution de l'état (Section 8.4). Cependant, dans ce cadre, «l'état» est l'état de l'information quantique d'un biosystème utilisé pour le traitement de l'incertitude quantique spéciale (section 8.2).
Observations
Dans les manuels de mécanique quantique, il est communément souligné que la principale caractéristique distinctive de la théorie quantique est la présence d'observables incompatibles. Rappelons que deux observables et sont incompatibles s'il est impossible de leur attribuer des valeurs conjointement. Dans le modèle probabiliste, cela conduit à l'impossibilité de déterminer leur distribution de probabilité conjointe (JPD). Les exemples de base d'observables incompatibles sont la position et la quantité de mouvement d'un système quantique, ou les projections de spin (ou de polarisation) sur différents axes. Dans le formalisme mathématique, l'incompatibilité est décrite comme la non-commutativité des opérateurs hermitiens et représentant les observables, c'est-à-dire
Nous nous référons ici au modèle original et toujours fondamental et largement utilisé des observables quantiques, Von Neumann 1955[23] (Section 3.2).
L'incompatibilité-non-commutativité est largement utilisée en physique quantique et les observables physiques de base, comme par exemple les projections de position et d'impulsion, de spin et de polarisation, sont traditionnellement représentées dans ce paradigme, par des opérateurs hermitiens. Nous pointons également de nombreuses applications de cette approche à la cognition, à la psychologie, à la prise de décision (Khrennikov, 2004a,[24] Busemeyer et Bruza, 2012,[25] Bagarello, 2019[26]) (voir notamment l'article (Bagarello et al., 2018[27]) qui est consacré à la quantification de la Relations d'incertitude de Heisenberg dans la prise de décision). Pourtant, ce n'est peut-être pas assez général pour notre objectif - à la modélisation de type quantique en biologie, aucun type de biostatistique non classique ne peut être facilement délégué au modèle d'observations de von Neumann. Par exemple, même des effets cognitifs très basiques ne peuvent pas être décrits d'une manière cohérente avec le modèle d'observation standard (Khrennikov et al., 2014,[28] Basieva et Khrennikov, 2015[29]).
Nous explorerons une théorie plus générale des observations basées sur des instruments quantiques (Davies et Lewis, 1970,[16] Davies, 1976,[17] Ozawa, 1984,[18] Yuen, 1987,[19] Ozawa, 1997,[20] Ozawa, 2004,[21] Okamura et Ozawa, 2016[22]) et trouverons des outils utiles pour applications à la modélisation des effets cognitifs (Ozawa et Khrennikov, 2020a,[30] Ozawa et Khrennikov, 2020b[31]). Nous discuterons de cette question dans la section 3 et l'illustrerons avec des exemples tirés de la cognition et de la biologie moléculaire dans les sections 6, 7. Dans le cadre de la théorie des instruments quantiques, le point crucial n'est pas la commutativité vs la non-commutativité des opérateurs représentant symboliquement des observables, mais la forme mathématique de la transformation d'état résultant de l'action inverse de l'(auto-)observation. Dans l'approche standard, cette transformation est donnée par une projection orthogonale sur le sous-espace des vecteurs propres correspondant à la sortie de l'observation. C'est le postulat de projection. Dans la théorie des instruments quantiques, les transformations d'état sont plus générales.
Le calcul des instruments quantiques est étroitement couplé à la théorie des systèmes quantiques ouverts (Ingarden et al., 1997[32]), systèmes quantiques interagissant avec les environnements. Nous remarquons que dans certaines situations, les systèmes physiques quantiques peuvent être considérés comme (au moins approximativement) isolés. Cependant, les biosystèmes sont fondamentalement ouverts. Comme l'a souligné Schrödinger (1944),[33] un biosystème complètement isolé est mort. Ce dernier explique pourquoi la théorie des systèmes quantiques ouverts et, en particulier, le calcul des instruments quantiques jouent le rôle fondamental dans les applications à la biologie, en tant qu'appareil mathématique de la biologie de l'information quantique (Asano et al., 2015a[14]).
Dans le cadre de la théorie des systèmes quantiques ouverts, nous modélisons l'évolution épigénétique (Asano et al., 2012b,[34] Asano et al., 2015b[35]) (Sections 9, 11.2) et la performance des fonctions psychologiques (cognitives) réalisées par le cerveau (Asano et al., 2011,[36] Asano et al., 2015b,[35] Khrennikov et al., 2018[12]) (Sections 10, 11.3).
Pour les biologistes suffisamment formés en mathématiques, mais sans connaissances en physique, nous pouvons recommander un livre (Khrennikov, 2016a[37]) combinant les présentations de CP et QP avec une brève introduction au formalisme quantique, y compris la théorie des instruments quantiques et les probabilités conditionnelles.
2. Probabilité classique contre probabilité quantique
CP a été formalisé mathématiquement par Kolmogorov (1933)[15] Il s'agit du calcul des mesures de probabilité, où un poids non négatif est attribué à tout événement . La principale propriété de CP est son additivité : si deux événements sont disjoints, alors la probabilité de disjonction de ces événements égale à la somme des probabilités :
QP est le calcul des amplitudes complexes ou dans le formalisme abstrait des vecteurs complexes. Ainsi, au lieu d'opérations sur des mesures de probabilité, on opère avec des vecteurs. On peut dire que QP est un modèle vectoriel de raisonnement probabiliste. Chaque amplitude complexe donne la probabilité par la règle de Born : la probabilité est obtenue comme le carré de la valeur absolue de l'amplitude complexe.
(pour la formalisation de l'espace de Hilbert, voir Section 3.2, formule (7)). En opérant avec des amplitudes de probabilité complexes, au lieu de l'opération directe avec des probabilités, on peut violer les lois fondamentales de CP. Dans CP, la formule de probabilité totale (FTP) est dérivée en utilisant l'additivité de la probabilité et la formule de Bayes, la définition de la probabilité conditionnelle, , Considérez la paire, et , de variables aléatoires classiques discrètes. Alors
Ainsi, dans CP, la distribution de probabilité peut être calculée à partir de la probabilité et des probabilités conditionnelles
Dans QP, la FTP classique est perturbée par le terme d'interférence (Khrennikov, 2010);[38] pour les observables quantiques dichotomiques et de type von Neumann, c'est-à-dire données par les opérateurs hermitiens et , la version quantique de FTP a la forme :
Si le terme d'interférence7 est positif, alors le calcul QP générerait une probabilité plus grande que son homologue CP donné par le FTP classique (2). En particulier, cette amplification de probabilité est à la base de la suprématie de l'informatique quantique.
De nombreuses données statistiques issues de la psychologie cognitive, de la prise de décision, de la biologie moléculaire, de la génétique et de l'épigénétique démontrent que les biosystèmes, des protéines et des cellules (Asano et al., 2015b[35]) aux humains (Khrennikov, 2010,[39] Busemeyer et Bruza, 2012[25]) utilisent cette amplification et fonctionner avec des mises à jour non-CP. Nous poursuivons notre présentation avec de tels exemples.
3. Instruments quantiques
3.1. Quelques mots sur le formalisme quantique
Dénotons par un espace de Hilbert complexe. Pour simplifier, nous supposons qu'il est de dimension finie. Les états purs d'un système sont donnés par des vecteurs normalisés de et les états mixtes par des opérateurs de densité (opérateurs semi-définis positifs avec trace unitaire). L'espace des opérateurs de densité est noté(). L'espace de tous les opérateurs linéaires en est désigné par le symbole . À son tour, il s'agit d'un espace linéaire. De plus, est l'espace de Hilbert complexe avec le produit scalaire, . Nous considérons des opérateurs linéaires agissant en . Ils sont appelés superopérateurs.
La dynamique de l'état pur d'un système quantique isolé est décrite par l'équation de Schrödinger :
où est l'hamiltonien du système. Cette équation implique que l'état pur évolue unitairement , où est un groupe paramétrique d'opérateurs unitaires, . En physique quantique, l'Hamiltonien est associé à l'énergie observable. La même interprétation est utilisée en biophysique quantique (Arndt et al., 2009[40]). Cependant, dans notre modélisation de type quantique décrivant le traitement de l'information dans les biosystèmes, l'opérateur n'a pas de couplage direct avec l'énergie physique. C'est le générateur d'évolution décrivant les interactions d'information.
La dynamique de Schrödinger pour un état pur implique que la dynamique d'un état mixte (représenté par un opérateur de densité) est décrite par l'équation de von Neumann :
3.2. Formalisme de Von Neumann pour les observables quantiques
Dans le formalisme quantique original (Von Neumann, 1955),[41] l'observable physique est représenté par un opérateur Hermitien . Nous ne considérons que les opérateurs avec des spectres discrets : où est le projecteur sur le sous-espace de correspondant à la valeur propre . Supposons que l'état du système est représenté mathématiquement par un opérateur de densité . Alors la probabilité d'obtenir la réponse est donnée par la Règle née
et selon le postulat de projection, l'état post-mesure est obtenu via la transformation d'état :
Pour la commodité du lecteur, nous présentons ces formules pour un état initial pur . La règle de Born a la forme :
La transformation d'état est donnée par le postulat de projection :
Ici, l'opérateur observable (sa décomposition spectrale) détermine de manière unique les transformations d'état de rétroaction pour les résultats
La carte donnée par (9) est l'exemple le plus simple (mais très important) d'instrument quantique.
3.3. Mise à jour d'état non projective : instruments atomiques
En général, les propriétés statistiques de toute mesure sont caractérisées par
- la distribution de probabilité de sortie , la distribution de probabilité de la sortie de la mesure dans l'état d'entrée 0 la réduction de l'état quantique
- la réduction d'état quantique , le changement d'état de l'état d'entrée à l'état de sortie conditionné par le résultat de la mesure.
Dans la formulation de von Neumann, les propriétés statistiques de toute mesure d'un observable sont uniquement déterminées par la règle de Born (5) et le postulat de projection (6), et elles sont représentées par la carte (9), un instrument de type von Neumann. Cependant, la formulation de von Neumann ne reflète pas le fait que le même observable représenté par l'opérateur Hermitien dans peut être mesuré de plusieurs façons8. Formellement, ces schémas de mesure sont représentés par des instruments quantiques.
Considérons maintenant les instruments quantiques les plus simples de type non von Neumann, dits instruments atomiques. Nous commençons par un rappel de la notion de POVM (Probability Operator Valued Measure) ; nous limitons les considérations aux POVM avec un domaine discret de définition . POVM est une carte telle que pour chaque est un opérateur Hermitien contractif positif (appelé effet) (c'est-à-dire ou tout ), et la condition de normalisation est vérifiée, où est l'opérateur d'unité. On suppose que pour toute mesure, la distribution de probabilité de sortie est donnée par
où est un POVM. Pour les instruments atomiques, on suppose que les effets sont représentés concrètement sous la forme
où est un opérateur linéaire en . Par conséquent, la condition de normalisation a la forme .9 La règle de Born peut être écrite de manière similaire à (5) :
On suppose que la transformation de l'état post-mesure est basée sur la carte :
| * |
donc la réduction de l'état quantique est donnée par
| * |
la carte donnée par (13) est un instrument quantique atomique. On remarque que la règle de Born (12) peut s'écrire sous la forme
| * | f |
Soit un opérateur hermitien en . Considérons un POVM avec le domaine de définition donné par le spectre de . Ce POVM représente une mesure de observable si la règle de Born est vérifiée :
Ainsi, en principe, les probabilités de résultats sont toujours encodées dans la décomposition spectrale de l'opérateur ou en d'autres termes les opérateurs 0doivent être sélectionnés de telle manière qu'ils génèrent les probabilités correspondant à la décomposition spectrale de la représentation symbolique des observables , c'est-à-dire que est déterminé de manière unique par en tant que . Nous pouvons dire que cet opérateur ne contient que des informations sur les probabilités des résultats, contrairement au schéma de von Neumann, l'opérateur ne code pas la règle de la mise à jour de l'état. Pour un instrument atomique, les mesures de l'observable ont la distribution de probabilité de sortie unique selon la règle de Born (16), mais ont de nombreuses réductions d'état quantique différentes en fonction de la décomposition de l'effet de telle manière que
3.4. Théorie générale (Davies-Lewis-Ozawa)
Enfin, nous formulons la notion générale d'instrument quantique. Un super-opérateur agissant dans appelé positif s'il mappe l'ensemble des opérateurs semi-définis positifs sur lui-même. Nous remarquons que, pour chaque donné par (13) peut être considéré comme une application positive linéaire.
Généralement, toute carte , où pour chaque , la carte est un superopérateur positif est appelée instrument quantique de Davies-Lewis (Davies et Lewis, 1970).[12]
Ici, l'indice 0désigne l'observable couplé à cet instrument. Les probabilités de résultats sont données par la règle de Born sous la forme (15) et la mise à jour d'état par transformation (14). Cependant, Yuen (1987)[42] a souligné que la classe des instruments Davies-Lewis est trop générale pour exclure les instruments physiquement non réalisables. Ozawa (1984)[14] a introduit la condition supplémentaire importante pour s'assurer que chaque instrument quantique est physiquement réalisable. C'est la condition de la positivité complète.
Un superopérateur est dit complètement positif si son extension naturelle au produit tensoriel est à nouveau un superopérateur positif sur . Une carte , où pour chaque , la carte est un superopérateur complètement positif est appelée Davies–Lewis–Ozawa (Davies et Lewis, 1970,[12] Ozawa, 1984[14]) instrument quantique ou simplement instrument quantique. Comme nous le verrons dans la section 4, la positivité complète est une condition suffisante pour qu'un instrument soit physiquement réalisable. D'autre part, la nécessité est dérivée comme suit (Ozawa, 2004).[43]
Chaque observable d'un système est identifié avec le observable d'un système avec tout système externe à .(10)
Ensuite, tout instrument physiquement réalisable mesurant doit être identifié avec l'instrument mesurant tel que . Cela implique que est à nouveau un super-opérateur positif, de sorte que est complètement positif.
De même, tout système de mesure d'instrument physiquement réalisable devrait avoir son instrument étendu système de mesure pour tout système externe . Ceci n'est rempli que si est complètement positif. Ainsi, la positivité complète est une condition nécessaire pour que décrive un instrument physiquement réalisable.
4. Instruments quantiques du schéma des mesures indirectes
Le modèle de base pour la construction d'instruments quantiques est basé sur le schéma de mesures indirectes. Ce schéma formalise la situation suivante : les sorties de mesure sont générées via l'interaction d'un système avec un appareil de mesure . Cet appareil consiste en un dispositif physique complexe interagissant avec et un pointeur qui affiche le résultat de la mesure, par exemple spin up ou spin down. Un observateur ne peut voir que les sorties du pointeur et il associe ces sorties aux valeurs de l'observable pour le système . Ainsi, le schéma de mesure indirect implique :
- les états des systèmes et des appareils
- l'opérateur représentant la dynamique d'interaction pour le système
- le mètre observable donnant les sorties du pointeur de l'appareil .
Un modèle de mesure indirecte, introduit dans Ozawa (1984)[12] comme un « processus de mesure (général) », est un quadruple
composé d'un espace de Hilbert , d'un opérateur de densité , d'un opérateur unitaire sur le produit tensoriel des espaces d'états de et et d'un opérateur Hermitien sur . Par ce modèle de mesure, l'espace de Hilbert décrit les états de l'appareil , l'opérateur unitaire décrit l'évolution temporelle du système composite , l'opérateur de densité décrit l'état initial de l'appareil et l'opérateur Hermitien décrit le mètre observable de l'appareil . Ensuite, la distribution de probabilité de sortie dans l'état du système est donnée par
où est la projection spectrale de pour la valeur propre . Le changement de l'état du système causé par la mesure pour le résultat est représenté à l'aide de la carte dans l'espace des opérateurs de densité définis comme
où est la trace partielle sur . Ensuite, la carte s'avère être un instrument quantique. Ainsi, les propriétés statistiques de la mesure réalisée par tout modèle de mesure indirect sont décrites par une mesure quantique. Remarquons qu'à l'inverse tout instrument quantique peut être représenté via le modèle de mesure indirecte (Ozawa, 1984).[12] Ainsi, les instruments quantiques caractérisent mathématiquement les propriétés statistiques de toutes les mesures quantiques physiquement réalisables.
5. Modélisation du processus de sensation-perception dans le cadre d'un schéma de mesure indirect
Les fondements de la théorie de l'inférence inconsciente pour la formation des impressions visuelles ont été établis au XIXe siècle par H. von Helmholtz. Bien que von Helmholtz ait étudié principalement la sensation-perception visuelle, il a également appliqué sa théorie à d'autres sens jusqu'à l'aboutissement de la théorie de l'inférence sociale inconsciente. Selon von Helmholtz, voici deux étapes du processus cognitif, et elles font la distinction entre la sensation et la perception comme suit :
- La sensation est un signal que le cerveau interprète comme un son ou une image visuelle, etc.
- La perception est quelque chose qui doit être interprété comme une préférence ou une attention sélective, etc.
Dans le schéma de mesure indirecte, les sensations représentent les états du système de sensation de l'humain et le système de perception joue le rôle de l'appareil de mesure. L'opérateur unitaire décrit le processus d'interaction entre les états de sensation et de perception. Cette modélisation quantique du processus de sensation-perception a été présentée dans un article (Khrennikov, 2015)[44] avec une application à la perception bistable et aux données expérimentales de l'article (Asano et al., 2014).[45]
6. Modélisation des effets cognitifs
En sciences cognitives et sociales, le pool d'opinion suivant est connu comme l'exemple de base de l'effet d'ordre. Il s'agit du pool d'opinion Clinton-Gore (Moore, 2002).[46] Dans cette expérience, les citoyens américains ont posé une question à la fois, par exemple,
- “Bill Clinton est-il honnête et digne de confiance ?”
- “Al Gore est-il honnête et digne de confiance ?”
Deux distributions de probabilités séquentielles ont été calculées sur la base des données statistiques expérimentales, et (première question puis question et vice versa).
6.1. Effet d'ordre pour l'interrogation séquentielle
Les données statistiques de cette expérience ont démontré l'effet d'ordre des questions QOE, dépendance de la distribution de probabilité conjointe séquentielle pour les réponses aux questions sur leur ordre . Nous remarquons que dans le modèle CP, ces distributions de probabilité coïncident :
où est un espace échantillon et est une mesure de probabilité.
QOE stimule l'application du calcul QP à la cognition, voir article (Wang et Busemeyer, 2013).[47] Les auteurs de cet article ont souligné que la caractéristique non commutative des probabilités conjointes peut être modélisée en utilisant la non commutativité d'observables quantiques incompatibles représentés par des opérateurs Hermitiens . L'observable représente la question de Clinton et l'observable représente la question de Gore. Dans ce modèle, QOE est identique incompatibilité-non-commutativité des observables :
6.2.Effet de réplicabilité des réponses pour les questions séquentielles
L'approche basée sur l'identification de l'effet d'ordre avec une représentation non commutative des questions (Wang et Busemeyer, 2013[48]) a été critiquée dans l'article (Khrennikov et al., 2014).[12] Pour discuter de cet article, nous rappelons la notion de réplicabilité de la réponse. Supposons qu'une personne, disons John, se voit poser une question et supposons qu'elle réponde, par exemple, "oui". Si immédiatement après cela, on lui pose à nouveau la même question, alors il répond « oui » avec une probabilité de un. Nous appelons cette propriété la réplicabilité de la réponse. En physique quantique, la réplicabilité de la réponse est exprimée par le postulat de projection. Le sondage d'opinion Clinton-Gore ainsi que les expériences de prise de décision typiques satisfont la réplicabilité de la réponse . La prise de décision a également une autre caractéristique - réplicabilité de la réponse. Supposons qu'après avoir répondu à la question en disant la réponse "oui", John se voit poser une autre question . Il y a répondu avec une réponse. Et puis on lui demande à nouveau . Dans le pool d'opinions sociales susmentionné, John répète sa réponse initiale à , "oui" (avec probabilité un).
Ce phénomène comportemental est appelé réplicabilité de la réponse . La combinaison de avec 0 et réplicabilité de réponse est appelée l'effet de réplicabilité de réponse RRE.
6.3. 'QOE+RRE': décrit par des instruments quantiques de type non projectif
Dans un article (Khrennikov et al., 2014),[12] il a été montré qu'en utilisant le calcul de von Neumann, il est impossible de combiner RRE avec QOE. Pour générer QOE, les opérateurs Hermitiens doivent être non commutatifs, mais ce dernier détruit la réplicabilité de la réponse de . C'était un résultat plutôt inattendu. Cela a même donné l'impression que, bien que les effets cognitifs de base puissent être modélisés séparément de manière quantique, leurs combinaisons ne peuvent pas être décrites par le formalisme quantique.
Cependant, récemment, il a été montré que la théorie des instruments quantiques fournit une solution simple de la combinaison des effets QOE et RRE, voir Ozawa et Khrennikov (2020a)[49] pour la construction de tels instruments. Ces instruments sont de type non projectif. Ainsi, l'essence de QOE n'est pas dans la structure des observables, mais dans la structure de la transformation d'état générée par la rétroaction des mesures. QOE ne concerne pas la mesure conjointe et l'incompatibilité (non-commutativité) des observables, mais la mesure séquentielle des observables et la mise à jour séquentielle de l'état (mental). Les instruments quantiques qui sont utilisés dans Ozawa et Khrennikov (2020a) pour combiner QOE et RRE correspondent à la mesure d'observables représentés par des opérateurs commutants . De plus, il est possible de prouver que (sous restriction mathématique naturelle) QOE et RRE ne peuvent être modélisés conjointement que à l'aide d'instruments quantiques pour faire la navette entre les observables.
6.4. Réalisme mental
Depuis le tout début de la mécanique quantique, la non-commutativité des opérateurs représentant les observables a été considérée comme la représentation mathématique de leur incompatibilité. En termes philosophiques, cette situation est traitée comme l'impossibilité de la description réaliste. En sciences cognitives, cela signifie qu'il existe des états mentaux tels qu'un individu ne peut pas attribuer les valeurs définies aux deux observables (par exemple, des questions). La description mathématique de QOE avec des observables représentées par des opérateurs non commutatifs (dans le schéma de von Neumann) dans Wang et Busemeyer (2013)[50] et Wang et al. (2014)[51] ont laissé entendre que cet effet implique le rejet du réalisme mental. Le résultat d'Ozawa et Khrennikov (2020a) [52]démontre que, malgré un QOE bien documenté expérimentalement, le réalisme mental n'a pas besoin d'être rejeté. Le QOE peut être modélisé dans l'image réaliste donnée mathématiquement par la distribution de probabilité conjointe des observables et , mais avec l'action non commutative des instruments quantiques mettant à jour l'état mental :
C'est le bon endroit pour remarquer que si, pour un état , alors QOE disparaît, même si . Cela peut être considéré comme la bonne formulation de la déclaration de Wang – Bussemeyer sur la connexion de QOE avec la non-commutativité. Au lieu de la non-commutativité des opérateurs et représentant symboliquement des observables quantiques, il faut parler de non-commutativité des instruments quantiques correspondants.
7. Génétique : interférence dans le métabolisme du glucose/lactose
Dans un article (Asano et al., 2012a[12]), un modèle de type quantique a été développé décrivant la régulation génique du métabolisme du glucose/lactose dans la bactérie Escherichia coli.11 Il existe plusieurs types d'E. coli caractérisés par le système métabolique. Il a été démontré que le type concret d'E. coli peut être décrit par les opérateurs linéaires bien déterminés ; on trouve les quantités d'opérateurs invariants caractérisant chaque type. De telles quantités d'opérateurs invariants peuvent être calculées à partir des données statistiques obtenues. Ainsi, la représentation de type quantique a été reconstruite à partir de données expérimentales.
Considérons qu'un système d'événements signifie l'événement où E. coli active son opéron lactose, c'est-à-dire l'événement où la -galactosidase est produite par la transcription de l'ARNm d'un gène dans l'opéron lactose ; 0 signifie l'événement où E. coli n'active pas son opéron lactose.
Ce système d'événements correspond à l'activation observable qui est représentée mathématiquement par un instrument quantique . Considérons maintenant un autre système d'événements où signifie l'événement qu'une bactérie E. coli détecte une molécule de lactose dans l'environnement environnant de la cellule, signifie détection d'un glucose moléculaire. Ce système d'événements correspond à la détection observable qui est représentée par un instrument quantique .
Dans ce modèle, l'interaction-réaction de la bactérie avec l'environnement glucose/lactose est décrite comme l'action séquentielle de deux instruments quantiques, d'abord la détection puis l'activation. Comme cela a été montré dans Asano et al. (2012a),[12] pour chaque type concret de bactérie E. coli, ces instruments quantiques peuvent être reconstruits à partir des données expérimentales ; dans Asano et al. (2012a),[12][12] la reconstruction a été réalisée pour la bactérie E. coli de type W3110. La FTP classique avec les observables et est violée, le terme d'interférence, voir (2), a été calculé (Asano et al., 2012a).[12]
8. Systèmes quantiques ouverts : interaction d'un biosystème avec son environnement
Comme cela a déjà été souligné, tout biosystème est fondamentalement ouvert. Par conséquent, la dynamique de son état doit être modélisée via une interaction avec l'environnement environnant . Les états de et sont représentés dans les espaces de Hilbert et . Le système composé est représenté dans les espaces de Hilbert du produit tensoriel. Ce système est traité comme un système isolé et conformément à la théorie quantique, la dynamique de son état pur peut être décrite par l'équation de Schrödinger :
où est l'état pur du système et est son hamiltonien. Cette équation implique que l'état pur évolue unitaire : . Ici Hamiltonien (générateur d'évolution) décrivant les interactions d'information a la forme , où , sont des Hamiltoniens des systèmes et est l'Hamiltonien d'interaction.(12) Cette équation implique que l'évolution de l'opérateur de densité du système est décrite par l'équation de von Neumann :
Cependant, l'état est trop complexe pour toute analyse mathématique : l'environnement comprend trop de degrés de liberté. Par conséquent, nous ne nous intéressons qu'à l'état ; sa dynamique est obtenue par traçage de l'état de w.r.t. les degrés de liberté de :
Généralement cette équation, l'équation maîtresse quantique, est mathématiquement très compliquée. Une variété d'approximations est utilisée dans les applications.
8.1. Modèle quantique de Markov : Équation de Gorini–Kossakowski–Sudarshan–Lindblade
L'approximation la plus simple de l'équation maîtresse quantique (23) est la dynamique de Markov quantique donnée par l'équation de Gorini-Kossakowski-Sudarshan-Lindblad (GKSL) (Ingarden et al., 1997)[53] (en physique, elle est communément appelée simplement l'équation de Lindblad ; c'est l'équation maîtresse quantique la plus simple):
où l'opérateur hermitien (Hamiltonien) décrit la dynamique interne de et le superopérateur , agissant dans l'espace des opérateurs de densité, décrit une interaction avec l'environnement . Ce superopérateur est souvent appelé Lindbladian. L'équation GKSL est une équation maîtresse quantique pour la dynamique markovienne. Dans cet article, nous n'avons pas la possibilité d'expliquer plus en détail la notion de Markovianité quantique. L'équation maîtresse quantique (23) décrit une dynamique généralement non markovienne.
8.2. Fonctions biologiques dans le cadre de Markov quantique
Nous nous tournons vers la dynamique du système ouvert avec l'équation GKSL. Dans notre modélisation, Hamiltonian et Lindbladian représentent une fonction biologique spéciale (voir Khrennikov et al., 2018)[54] pour plus de détails. Son fonctionnement résulte de l'interaction des flux d'informations internes et externes. Dans les sections 10, 11.3, est une fonction psychologique; dans le cas le plus simple représente une question posée à (disons est un être humain). Dans la section 7, est la régulation génique du métabolisme du glucose/lactose dans la bactérie Escherichia coli. Dans les sections 9, 11.2, représente le processus de mutation épigénétique. Symboliquement, la fonction biologique est représentée comme une observable quantique : opérateur Hermitien avec la décomposition spectrale , où marque les sorties de . La théorie de la dynamique des états quantiques de Markov décrit le processus de génération de ces sorties.
Dans le modèle mathématique (Asano et al., 2015b,[55] Asano et al., 2017b,[56] Asano et al., 2017a,[57] Asano et al., 2015a,[58] Asano et al., 2012b,[59] Asano et al., 2011,[60] Asano et al. ., 2012a[61]), les sorties de la fonction biologique sont générées en approchant un état stable de la dynamique GKSL :
telle qu'elle corresponde à la décomposition spectrale de , i.e.,
où
Cela signifie que est diagonal dans une base orthonormée constituée de vecteurs propres de . Cet état, ou plus précisément cette décomposition de l'opérateur de densité , est le mélange statistique classique des états d'information de base déterminant cette fonction biologique. Les probabilités dans la décomposition de l'état (26) sont interprétées statistiquement.
Considérons un grand ensemble de biosystèmes avec l'état interagissant avec l'environnement . (Nous rappelons que mathématiquement l'interaction est codée dans le Lindbladian ) Résultant de cette interaction, la fonction biologique produit la sortie avec probabilité . Nous remarquons que dans l'opérateur termes la probabilité est exprimée par
Cette interprétation peut être appliquée même à un seul biosystème qui rencontre plusieurs fois le même environnement. Il convient de noter que l'état limite exprime la stabilité par rapport à l'influence de l'environnement concret . Bien sûr, dans le monde réel, l'état limite ne serait jamais approché. La formule mathématique (25) décrit le processus de stabilisation, d'amortissement des fluctuations. Mais, ils ne disparaîtraient jamais complètement avec le temps.
Nous notons qu'un état stationnaire satisfait l'équation GKSL stationnaire :
Il est également important de souligner que généralement un état stationnaire de l'équation maîtresse quantique n'est pas unique, il dépend de la classe des conditions initiales.
8.3. Fonctionnement des fonctions biologiques par décohérence
Pour concrétiser les considérations précédentes, considérons un état quantique pur comme état initial. Supposons qu'une fonction biologique soit dichotomique, , et qu'elle soit symboliquement représentée par l'opérateur hermitien qui est diagonal en base orthonormée , . (Nous considérons l'espace d'états à deux dimensions - l'espace qubit.) Soit l'état initial a la forme d'une superposition
où . La dynamique maître quantique n'est pas une dynamique d'état pur : tôt ou tard (en fait, très bientôt), cette superposition représentant un état pur sera transférée dans une matrice de densité représentant un état mixte. Par conséquent, dès le début, il est utile de représenter la superposition (28) en termes de matrice de densité :
La pureté de l'état, la superposition, est caractérisée par la présence de termes non nuls hors diagonale.
La superposition code l'incertitude par rapport à la base de l'état concret, dans notre cas ,. Initialement, la fonction biologique était dans l'état d'incertitude entre deux choix . Il s'agit d'une véritable incertitude quantique (de type). Incertitude, sur les actions possibles à l'avenir. Par exemple, pour la fonction psychologique (Section 10) représentant la réponse à une question, disons "acheter une propriété" () et sa négation (), une personne dont l'état est décrit par la superposition (28) est incertaine d'agir avec () ou avec () . Ainsi, un état de type superposition décrit l'incertitude individuelle, c'est-à-dire l'incertitude associée au biosystème individuel et non à un ensemble de biosystèmes ; avec le seul acte de fonctionnement de et non avec une grande série de tels actes.
Résolution de l'incertitude par rapport à est caractérisé par le lavage des termes hors diagonale dans (29) La dynamique quantique (24) supprime les termes hors diagonale et, enfin, une matrice de densité diagonale représentant un état stationnaire de ces systèmes dynamiques est générée :
Il s'agit d'un mélange statistique classique. Il décrit un ensemble de biosystèmes ; statistiquement, ils génèrent des sorties avec des probabilités . De la même manière, l'interprétation statistique peut être utilisée pour un système unique qui effectue un fonctionnement à différentes instances de temps (pour une longue série temporelle).
En physique quantique, le processus de lavage des éléments hors diagonale dans une matrice de densité est connu sous le nom de processus de décohérence. Ainsi, le modèle décrit peut être appelé fonctionnement de la fonction biologique par décohérence.
8.4. Linéarité de la représentation quantique : accélération exponentielle du fonctionnement biologique
La modélisation de type quantique ne prétend pas que les biosystèmes sont fondamentalement quantiques. Une image plus naturelle est qu'il s'agit de systèmes biophysiques classiques complexes et que le modèle de type quantique fournit la représentation de l'information des processus biophysiques classiques, dans les gènes, les protéines, les cellules, les cerveaux. Un des avantages de cette représentation est sa linéarité. L'espace d'état quantique est un espace de Hilbert complexe et les équations dynamiques sont des équations différentielles linéaires. Pour les espaces d'états de dimension finie, ce ne sont que des équations différentielles ordinaires avec des coefficients complexes (ainsi, le lecteur ne devrait pas avoir peur de noms aussi pathétiques que Schrödinger, von Neumann ou équations de Gorini-Kossakowski-Sudarshan-Lindblad). La dynamique biophysique classique au-delà de la représentation de l'information quantique est généralement non linéaire et très compliquée. L'utilisation de la représentation spatiale linéaire simplifie la structure de traitement. Il y a deux points de vue sur cette simplification, externe et interne. Le premier est la simplification de la modélisation mathématique, c'est-à-dire la simplification de l'étude des bioprocédés (par nous, observateurs externes). La seconde est plus délicate et intéressante. Nous avons déjà signalé une importante spécialité des applications de la théorie quantique à la biologie. Ici, les systèmes peuvent effectuer des auto-observations. Ainsi, dans le processus d'évolution, disons qu'une cellule peut "apprendre" via de telles auto-observations qu'il est rentable sur le plan informatique d'utiliser la représentation linéaire de type quantique. Et maintenant, nous arrivons au principal avantage de la linéarité.
La dynamique linéaire accélère de façon exponentielle le traitement de l'information. Les solutions de l'équation GKSL peuvent être représentées sous la forme , où est le superopérateur donné par le côté droit de l'équation GKSL. Dans le cas de dimension finie, la dynamique de décohérence est exprimée via des facteurs de la forme , où . Ces facteurs diminuent de façon exponentielle. La réalisation linéaire de type quantique des fonctions biologiques est exponentiellement rapide par rapport à la dynamique classique non linéaire.
L'utilisation de la représentation de l'information quantique signifie que généralement de grands groupes d'états biophysiques classiques sont codés par quelques états quantiques. Cela signifie une énorme compression d'informations. Cela implique également une augmentation de la stabilité dans le traitement d'état. La dynamique classique non linéaire bruyante est mappée à une dynamique pilotée par une équation quantique linéaire (de type) de type GKSL.
Ce dernier a une structure essentiellement plus simple et via la sélection des coefficients d'opérateur codant symboliquement l'interaction au sein du système et avec son environnement environnant peut établir une dynamique avec des régimes de stabilisation conduisant à des états stationnaires.
9. Epigenetic evolution within theory of open quantum systems
In paper (Asano et al., 2012b), a general model of the epigenetic evolution unifying neo-Darwinian with neo-Lamarckian approaches was created in the framework of theory of open quantum systems. The process of evolution is represented in the form of adaptive dynamics given by the quantum(-like) master equation describing the dynamics of the information state of epigenome in the process of interaction with surrounding environment. This model of the epigenetic evolution expresses the probabilities for observations which can be done on epigenomes of cells; this (quantum-like) model does not give a detailed description of cellular processes. The quantum operational approach provides a possibility to describe by one model all known types of cellular epigenetic inheritance.
To give some hint about the model, we consider one gene, say . This is the system in Section 8.1. It interacts with the surrounding environment a cell containing this gene and other cells that send signals to this concrete cell and through it to the gene . As a consequence of this interaction some epigenetic mutation in the gene can happen. It would change the level of the -expression.
For the moment, we ignore that there are other genes. In this oversimplified model, the mutation can be described within the two dimensional state space, complex Hilbert space (qubit space). States of without and with mutation are represented by the orthogonal basis ,; these vectors express possible epigenetic changes of the fixed type .
A pure quantum information state has the form of superposition.
Now, we turn to the general scheme of Section 8.2 with the biological function expressing -epimutation in one fixed gene. The quantum Markov dynamics (24) resolves uncertainty encoded in superposition (“modeling epimutations as decoherence”). The classical statistical mixture , see (30), is approached. Its diagonal elements give the probabilities of the events: “no -epimutation” and “-epimutation”. These probabilities are interpreted statistically: in a large population of cells, cells, , the number of cells with -epimutation is . This -epimutation in a cell population would stabilize completely to the steady state only in the infinite time. Therefore in reality there are fluctuations (of decreasing amplitude) in any finite interval of time.
Finally, we point to the advantage of the quantum-like dynamics of interaction of genes with environment — dynamics’ linearity implying exponential speed up of the process of epigenetic evolution (Section 8.4).
10. Connecting electrochemical processes in neural networks with quantum informational processing
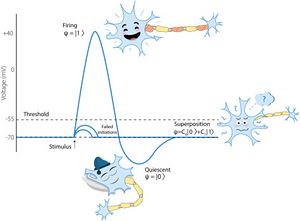
As was emphasized in introduction, quantum-like models are formal operational models describing information processing in biosystems. (in contrast to studies in quantum biology — the science about the genuine quantum physical processes in biosystems). Nevertheless, it is interesting to connect the structure quantum information processing in a biosystem with physical and chemical processes in it. This is a problem of high complexity. Paper (Khrennikov et al., 2018) presents an attempt to proceed in this direction for the human brain — the most complicated biosystem (and at the same time the most interesting for scientists). In the framework of quantum information theory, there was modeled information processing by brain’s neural networks. The quantum information formalization of the states of neural networks is coupled with the electrochemical processes in the brain. The key-point is representation of uncertainty generated by the action potential of a neuron as quantum(-like) superposition of the basic mental states corresponding to a neural code, see Fig. 1 for illustration.
Consider information processing by a single neuron; this is the system (see Section 8.2). Its quantum information state corresponding to the neural code quiescent and firing, , can be represented in the two dimensional complex Hilbert space (qubit space). At a concrete instant of time neuron’s state can be mathematically described by superposition of two states, labeled by ,: . It is assumed that these states are orthogonal and normalized, i.e., and, . The coordinates and with respect to the quiescent-firing basis are complex amplitudes representing potentialities for the neuron to be quiescent or firing. Superposition represents uncertainty in action potential, “to fire” or “not to fire”. This superposition is quantum information representation of physical, electrochemical uncertainty.
Let be some psychological (cognitive) function realized by this neuron. (Of course, this is oversimplification, considered, e.g., in the paradigm “grandmother neuron”; see Section 11.3 for modeling of based on a neural network). We assume that is dichotomous. Say represents some instinct, e.g., aggression: “attack” , “not attack” .
A psychological function can represent answering to some question (or class of questions), solving problems, performing tasks. Mathematically is represented by the Hermitian operator that is diagonal in the basis ,. The neuron interacts with the surrounding electrochemical environment . This interaction generates the evolution of neuron’s state and realization of the psychological function . We model dynamics with the quantum master equation (24). Decoherence transforms the pure state into the classical statistical mixture (30), a steady state of this dynamics. This is resolution of the original electrochemical uncertainty in neuron’s action potential.
The diagonal elements of give the probabilities with the statistical interpretation: in a large ensemble of neurons (individually) interacting with the same environment , say neurons, , the number of neurons which take the decision equals to the diagonal element .
We also point to the advantage of the quantum-like dynamics of the interaction of a neuron with its environment — dynamics’ linearity implying exponential speed up of the process of neuron’s state evolution towards a “decision-matrix” given by a steady state (Section 8.4).
11. Compound biosystems
11.1. Entanglement of information states of biosystems
The state space of the biosystem consisting of the subsystems , is the tensor product of subsystems’ state spaces , so
| * |
The easiest way to imagine this state space is to consider its coordinate representation with respect to some basis constructed with bases in . For simplicity, consider the case of qubit state spaces let , , be some orthonormal basis in , i.e., elements of this space are linear combinations of the form . (To be completely formal, we have to label basis vectors with the index , i.e.,. But we shall omit this it.) Then vectors form the orthonormal basis in , i.e., any state can be represented in the form
and the complex coordinates are normalized: . For example, if , we can consider the state
This is an example of an entangled state, i.e., a state that cannot be factorized in the tensor product of the states of the subsystems. An example of a non-entangled state (up to normalization) is given by
Entangled states are basic states for quantum computing that explores state’s inseparability. Acting to one concrete qubit modifies the whole state. For a separable state, by transforming say the first qubit, we change only the state of system . This possibility to change the very complex state of a compound system via change of the local state of a subsystem is considered as the root of superiority of quantum computation over classical one. We remark that the dimension of the tensor product state space is very big, it equals for qubit subsystems. In quantum physics, this possibility to manipulate with the compound state (that can have the big dimension) is typically associated with “quantum nonlocality” and spooky action at a distance.But, even in quantum physics this nonlocal interpretation is the source for permanent debates []. In particular, in the recent series of papers [] it was shown that it is possible to proceed without referring to quantum nonlocality and that quantum mechanics can be interpreted as the local physical theory. The local viewpoint on the quantum theory is more natural for biological application.13 For biosystems, spooky action at a distance is really mysterious; for humans, it corresponds to acceptance of parapsychological phenomena.
How can one explain generation of state-transformation of the compound system by “local transformation” of say the state of its subsystem ? Here the key-role is played by correlations that are symbolically encoded in entangled states. For example, consider the compound system in the state given by (33). Consider the projection-type observables on represented by Hermitian operators with eigen-vectors , (in qubit spaces ). Measurement of say with the output induces the state projection onto the vector .
Hence, measurement of will automatically produce the output . Thus, the state encodes the exact correlations for these two observables. In the same way, the state
encodes correlations , (mod 2).
So, 'an entangled state provides the symbolic representation of correlations between states of the subsystems of a compound biosystem'
Theory of open quantum systems operates with mixed states described by density operators. And before to turn to modeling of biological functions for compound systems, we define entanglement for mixed states. Consider the case of tensor product of two Hilbert spaces, i.e., the system is compound of two subsystems and . A mixed state of given by is called separable if it can be represented as a convex combination of product states , where , , are the density operator of the subsystem of . Non-separable states are called entangled. They symbolically represent correlations between subsystems.
Quantum dynamics describes the evolution of these correlations. In the framework of open system dynamics, a biological function approaches the steady state via the process of decoherence. As was discussed in Section 8.3, this dynamics resolves uncertainty that was initially present in the state of a biosystem; at the same time, it also washes out the correlations: the steady state which is diagonal in the basis is separable (disentagled). However, in the process of the state-evolution correlations between subsystems (entanglement) play the crucial role. Their presence leads to transformations of the state of the compound system via “local transformations” of the states of its subsystems. Such correlated dynamics of the global information state reflects consistency of the transformations of the states of subsystems.
Since the quantum-like approach is based on the quantum information representation of systems’ states, we can forget about the physical space location of biosystems and work in the information space given by complex Hilbert space . In this space, we can introduce the notion of locality based on the fixed tensor product decomposition (31). Operations in its components we can call local (in information space). But, they induce “informationally nonlocal” evolution of the state of the compound system.
11.2. Entanglement of genes’ epimutations
Now, we come back to the model presented in Section 9 and consider the information state of cell’s epigenome expressing potential epimutations of the chromatin-marking type. Let cell’s genome consists of genes . For each gene , consider all its possible epimutations and enumerate them: . The state of all potential epimutations in the gene is represented as superposition
In the ideal situation – epimutations of the genes are independent – the state of cell’s epigenome is mathematically described by the tensor product of the states :
However, in a living biosystem, the most of the genes and proteins are correlated forming a big network system. Therefore, one epimutation affects other genes. In the quantum information framework, this situation is described by entangled states:
This form of representation of potential epimutations in the genome of a cell implies that epimutation in one gene is consistent with epimutations in other genes. If the state is entangled (not factorized), then by acting, i.e., through change in the environment, to one gene, say , and inducing some epimutation in it, the cell “can induce” consistent epimutations in other genes.
Linearity of the quantum information representation of the biophysical processes in a cell induces the linear state dynamics. This makes the epigenetic evolution very rapid; the off-diagonal elements of the density matrix decrease exponentially quickly. Thus, our quantum-like model justifies the high speed of the epigenetic evolution. If it were based solely on the biophysical representation with nonlinear state dynamics, it would be essentially slower.
Modeling based on theory of open systems leads to reconsideration of interrelation between the Darwinian with Lamarckian viewpoint on evolution. Here we concentrated on epimutations, but in the same way we can model mutations (Asano et al., 2015b).
11.3. Psychological functions
Now, we turn to the model presented in Section 10. A neural network is modeled as a compound quantum system; its state is presented in tensor product of single-neuron state spaces. Brain’s functions perform self-measurements modeled within theory of open quantum systems. (There is no need to consider state’s collapse.) State’s dynamics of some brain’s function (psychological function) is described by the quantum master equation. Its steady states represent classical statistical mixtures of possible outputs of (decisions). Thus through interaction with electrochemical environment, (considered as an open system) resolves uncertainty that was originally encoded in entangled state representing uncertainties in action potentials of neurons and correlations between them.
Entanglement plays the crucial role in generating consistency in neurons’ dynamics. As in Section 11.1, suppose that the quantum information representation is based on 0–1 code. Consider a network of neurons interacting with the surrounding electrochemical environment , including signaling from other neural networks. The information state is given by (32). Entanglement encodes correlations between firing of individual neurons. For example, the state (33) is associated with two neurons firing synchronically and the state (34) with two neurons firing asynchronically.
Outputs of the psychological function based biophysically on a neural network are resulted from consistent state dynamics of individual neurons belonging to this network. As was already emphasized, state’s evolution toward a steady state is very rapid, as a consequence of linearity of the open system dynamics; the off-diagonal elements of the density matrix decrease exponentially quickly.
12. Concluding remarks
Since 1990th (Khrennikov, 1999), quantum-like modeling outside of physics, especially modeling of cognition and decision making, flowered worldwide. Quantum information theory (coupled to measurement and open quantum systems theories) is fertile ground for quantum-like flowers. The basic hypothesis presented in this paper is that functioning of biosystems is based on the quantum information representation of their states. This representation is the output of the biological evolution. The latter is considered as the evolution in the information space. So, biosystems react not only to material or energy constraints imposed by the environment, but also to the information constraints. In this paper, biological functions are considered as open information systems interacting with information environment.
The quantum-like representation of information provides the possibility to process superpositions. This way of information processing is advantageous as saving computational resources: a biological function need not to resolve uncertainties encoded in superpositions and to calculate JPDs of all compatible variables involved in the performance of .
Another advantageous feature of quantum-like information processing is its linearity. Transition from nonlinear dynamics of electrochemical states to linear quantum-like dynamics tremendously speeds up state-processing (for gene-expression, epimutations, and generally decision making). In this framework, decision makers are genes, proteins, cells, brains, ecological systems.
Biological functions developed the ability to perform self-measurements, to generate outputs of their functioning. We model this ability in the framework of open quantum systems, as decision making through decoherence. We emphasize that this model is free from the ambiguous notion of collapse of the wave function.
Correlations inside a biological function as well as between different biological functions and environment are represented linearly by entangled quantum states.
We hope that this paper would be useful for biologists (especially working on mathematical modeling) as an introduction to the quantum-like approach to model functioning of biosystems. We also hope that it can attract attention of experts in quantum information theory to the possibility to use its formalism and methodology in biological studies.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
This work was partially supported by JSPS, Japan KAKENHI, Nos. 26247016and 17K19970. M.O. acknowledges the support of the IRI-NU collaboration, Japan .
- ↑ Newton Isaac, «Philosophiae naturalis principia mathematica», Benjamin Motte, 1687, London UK».
- ↑ Kolmogorov A.N.Grundbegriffe Der Wahrscheinlichkeitsrechnung. Springer-Verlag, Berlin (1933)
- ↑ Penrose R. The Emperor’S New Mind Oxford Univ. Press, New-York (1989)
- ↑ Umezawa H. Advanced Field Theory: Micro, Macro and Thermal Concepts AIP, New York (1993)
- ↑ Hameroff S. Quantum coherence in microtubules. a neural basis for emergent con- sciousness? J. Cons. Stud., 1 (1994)
- ↑ Vitiello G. Dissipation and memory capacity in the quantum brain model Internat. J. Modern Phys. B, 9 (1995), p. 973
- ↑ Vitiello G. My Double Unveiled: The Dissipative Quantum Model of Brain, Advances in Consciousness Research, John Benjamins Publishing Company(2001)
- ↑ Arndt M., Juffmann T., Vedral V. Quantum physics meets biology HFSP J., 3 (6) (2009), pp. 386-400, 10.2976/1.3244985
- ↑ Bernroider G., Summhammer J. Can quantum entanglement between ion transition states effect action potential initiation? Cogn. Comput., 4 (2012), pp. 29-37
- ↑ Bernroider G. Neuroecology: Modeling neural systems and environments, from the quantum to the classical level and the question of consciousness J. Adv. Neurosci. Res., 4 (2017), pp. 1-9
- ↑ Plotnitsky A. Epistemology and Probability: Bohr, Heisenberg, SchrÖdinger and the Nature of Quantum-Theoretical Thinking Springer, Berlin, Germany; New York, NY, USA (2009
- ↑ 12.00 12.01 12.02 12.03 12.04 12.05 12.06 12.07 12.08 12.09 12.10 12.11 12.12 12.13 Khrennikov A., Basieva I., PothosE.M., Yamato I. Quantum Probability in Decision Making from Quantum Information Representation of Neuronal States, Sci. Rep., 8 (2018), Article 16225 Cite error: Invalid
<ref>tag; name ":0" defined multiple times with different content Cite error: Invalid<ref>tag; name ":0" defined multiple times with different content Cite error: Invalid<ref>tag; name ":0" defined multiple times with different content Cite error: Invalid<ref>tag; name ":0" defined multiple times with different content - ↑ Khrennikov A. On quantum-like probabilistic structure of mental information Open Syst. Inf. Dyn., 11 (3) (2004), pp. 267-275
- ↑ 14.0 14.1 14.2 14.3 Asano M., Basieva I., Khrennikov A., Ohya M., Tanaka Y., Yamato I. Quantum information biology: from information interpretation of quantum mechanics to applications in molecular biology and cognitive psychology Found. Phys., 45 (10) (2015), pp. 1362-1378 Cite error: Invalid
<ref>tag; name ":1" defined multiple times with different content - ↑ 15.0 15.1 Kolmogorov A.N. Grundbegriffe Der Wahrscheinlichkeitsrechnung Springer-Verlag, Berlin (1933)
- ↑ 16.0 16.1 Davies E.B., Lewis J.T. An operational approach to quantum probability Comm. Math. Phys., 17 (1970), pp. 239-260
- ↑ 17.0 17.1 Davies E.B. Quantum Theory of Open Systems. Academic Press, London (1976)
- ↑ 18.0 18.1 Ozawa M. Quantum measuring processes for continuous observables J. Math. Phys., 25 (1984), pp. 79-87
- ↑ 19.0 19.1 Yuen, H. P., 1987. Characterization and realization of general quantum measurements. M. Namiki and others (ed.) Proc. 2nd Int. Symp. Foundations of Quantum Mechanics, pp. 360–363.
- ↑ 20.0 20.1 Ozawa M. An operational approach to quantum state reduction Ann. Phys., NY, 259 (1997), pp. 121-137
- ↑ 21.0 21.1 Ozawa M. Uncertainty relations for noise and disturbance in generalized quantum measurements Ann. Phys., NY, 311 (2004), pp. 350-416
- ↑ 22.0 22.1 Okamura K., Ozawa M. Measurement theory in local quantum physics J. Math. Phys., 57 (2016), Article 015209
- ↑ Von Neumann J. Mathematical Foundations of Quantum Mechanics Princeton Univ. Press, Princeton, NJ, USA (1955)
- ↑ Khrennikov A. Information Dynamics in Cognitive, Psychological, Social, and Anomalous Phenomena, Ser.: Fundamental Theories of Physics, Kluwer, Dordreht(2004)
- ↑ 25.0 25.1 Busemeyer J., Bruza P. Quantum Models of Cognition and Decision Cambridge Univ. Press, Cambridge(2012)
- ↑ Bagarello F. Quantum Concepts in the Social, Ecological and Biological Sciences Cambridge University Press, Cambridge (2019)
- ↑ Bagarello F., Basieva I., Pothos E.M., Khrennikov A. Quantum like modeling of decision making: Quantifying uncertainty with the aid of heisenberg-robertson inequality J. Math. Psychol., 84 (2018), pp. 49-56
- ↑ Khrennikov A., Basieva I., DzhafarovE.N., Busemeyer J.R. Quantum models for psychological measurements: An unsolved problem. PLoS One, 9 (2014), Article e110909
- ↑ Basieva I., Khrennikov A. On the possibility to combine the order effect with sequential reproducibility for quantum measurements Found. Phys., 45 (10) (2015), pp. 1379-1393
- ↑ Ozawa M., Khrennikov A. Application of theory of quantum instruments to psychology: Combination of question order effect with response replicability effect Entropy, 22 (1) (2020), pp. 37.1-9436
- ↑ Ozawa M., Khrennikov A. Modeling combination of question order effect, response replicability effect, and QQ-equality with quantum instruments (2020)
- ↑ Ingarden R.S., Kossakowski A., Ohya M. Information Dynamics and Open Systems: Classical and Quantum Approach Kluwer, Dordrecht (1997)
- ↑ Schrödinger E. What Is Life? Cambridge university press, Cambridge (1944)
- ↑ Asano M., Basieva I., Khrennikov A., Ohya M., Tanaka Y., Yamato I. Towards modeling of epigenetic evolution with the aid of theory of open quantum systems AIP Conf. Proc., 1508 (2012), p. 75 https://aip.scitation.org/doi/abs/10.1063/1.4773118
- ↑ 35.0 35.1 35.2 Asano M., Khrennikov A., Ohya M., Tanaka Y., Yamato I. Quantum Adaptivity in Biology: From Genetics To Cognition Springer, Heidelberg-Berlin-New York(2015)
- ↑ Asano M., Ohya M., Tanaka Y., BasievaI., Khrennikov A. Quantum-like model of brain’s functioning: decision making from decoherence J. Theor. Biol., 281 (1) (2011), pp. 56-64
- ↑ Khrennikov A. Probability and Randomness: Quantum Versus Classical Imperial College Press (2016)
- ↑ Khrennikov A. Ubiquitous Quantum Structure: From Psychology To Finances Springer, Berlin-Heidelberg-New York(2010)
- ↑ Khrennikov A. Ubiquitous Quantum Structure: From Psychology To Finances Springer, Berlin-Heidelberg-New York(2010)
- ↑ Arndt M., Juffmann T., Vedral V. Quantum physics meets biology HFSP J., 3 (6) (2009), pp. 386-400,
- ↑ Von Neumann J. Mathematical Foundations of Quantum Mechanics Princeton Univ. Press, Princeton, NJ, USA(1955)
- ↑ Yuen, H. P., 1987. Characterization and realization of general quantum measurements. M. Namiki and others (ed.) Proc. 2nd Int. Symp. Foundations of Quantum Mechanics, pp. 360–363.
- ↑ Ozawa M. Uncertainty relations for noise and disturbance in generalized quantum measurements Ann. Phys., NY, 311 (2004), pp. 350-416
- ↑ Khrennikov A. A quantum-like model of unconscious-conscious dynamics. Front. Psychol., 6 (2015), Article 997
- ↑ Asano M., Khrennikov A., Ohya M., Tanaka Y., Yamato I. Violation of contextual generalization of the leggett-garg inequality for recognition of ambiguous figures. Phys. Scripta T, 163 (2014), Article 014006
- ↑ Moore D.W. Measuring new types of question-order effects. Public Opin. Quart., 60 (2002), pp. 80-91
- ↑ Wang Z., Busemeyer J.R. A quantum question order model supported by empirical tests of an a priori and precise prediction. Top. Cogn. Sci., 5 (2013), pp. 689-710
- ↑ Wang Z., Busemeyer J.R. A quantum question order model supported by empirical tests of an a priori and precise prediction. Top. Cogn. Sci., 5 (2013), pp. 689-710
- ↑ Ozawa M., Khrennikov A. Application of theory of quantum instruments to psychology: Combination of question order effect with response replicability effect. Entropy, 22 (1) (2020), pp. 37.1-9436
- ↑ Wang Z., Busemeyer J.R. A quantum question order model supported by empirical tests of an a priori and precise prediction. Top. Cogn. Sci., 5 (2013), pp. 689-710
- ↑ Wang Z., Solloway T., Shiffrin R.M., Busemeyer J.R. Context effects produced by question orders reveal quantum nature of human judgments. Proc. Natl. Acad. Sci. USA, 111 (2014), pp. 9431-9436
- ↑ Ozawa M., Khrennikov A. Application of theory of quantum instruments to psychology: Combination of question order effect with response replicability effect. Entropy, 22 (1) (2020), pp. 37.1-9436
- ↑ Ingarden R.S., Kossakowski A., Ohya M. Information Dynamics and Open Systems: Classical and Quantum Approach. Kluwer, Dordrecht (1997)
- ↑ Khrennikov A., Basieva I., Pothos E.M., Yamato I. Quantum Probability in Decision Making from Quantum Information Representation of Neuronal States, Sci. Rep., 8 (2018), Article 16225
- ↑ Asano M., Khrennikov A., Ohya M., Tanaka Y., Yamato I. Quantum Adaptivity in Biology: From Genetics To Cognition Springer, Heidelberg-Berlin-New York(2015)
- ↑ Asano M., Basieva I., Khrennikov A., Yamato I. A model of differentiation in quantum bioinformatics. Prog. Biophys. Mol. Biol., 130 (Part A)(2017), pp. 88-98
- ↑ Asano M., Basieva I., Khrennikov A., Ohya M., Tanaka Y. A quantum-like model of selection behavior. J. Math. Psychol., 78 (2017), pp. 2-12
- ↑ Asano M., Basieva I., Khrennikov A., Ohya M., Tanaka Y., Yamato I. Quantum information biology: from information interpretation of quantum mechanics to applications in molecular biology and cognitive psychology. Found. Phys., 45 (10) (2015), pp. 1362-1378
- ↑ Asano M., Basieva I., Khrennikov A., Ohya M., Tanaka Y., Yamato I. Towards modeling of epigenetic evolution with the aid of theory of open quantum systems AIP Conf. Proc., 1508 (2012), p. 75
- ↑ Asano M., Ohya M., Tanaka Y., BasievaI., Khrennikov A. Quantum-like model of brain’s functioning: decision making from decoherence. J. Theor. Biol., 281 (1) (2011), pp. 56-64
- ↑ Asano M., Basieva I., Khrennikov A., Ohya M., Tanaka Y., I Yamato quantum-like model for the adaptive dynamics of the genetic regulation of e. coli’s metabolism of glucose/lactose Syst. Synth. Biol., 6 (2012), pp. 1-7
particularly focusing on the field of the neurophysiology of the masticatory system




![{\displaystyle [{\hat {A}},{\hat {B}}]\neq 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca6253a4b7d1fed6f0b83ee4f14d05f740af438)
























![{\displaystyle {\frac {d{\hat {\rho }}}{dt}}(t)=-i[{\hat {\mathcal {H}}},{\hat {\rho }}(t)],{\hat {\rho }}(0)={\hat {\rho }}_{0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/46cb03104a69d14e36fd6776550cc38a492b9634)





![{\textstyle Pr\{A=x||\rho \}=Tr[{\widehat {E}}^{A}(x)\rho ]=Tr[{\widehat {E}}^{A}(x)\rho {\widehat {E}}^{A}(x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dffc6a2b1bbc16202b1abab10b045f1fcc304c04)






















![{\textstyle Pr\{{\text{x}}=x||\rho \}=Tr[{\hat {D}}(x)\rho ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/229874a62a1d92651c5a1e60265399c0e969dd05)






![{\textstyle Pr\{{\text{x}}=x||\rho \}=Tr[{V}(x)\rho {V}^{*}(x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd51eeb8f4e5b9cd30d856040525bb2be6f94c0b)



![{\textstyle \rho \rightarrow \rho _{({\text{x}}=x)}={\frac {{\mathcal {L}}_{A}(x)\rho }{Tr[{\mathcal {L}}_{A}(x)\rho ]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c622ed9f3472b9bc13374d7bd37e7da807ab612)


![{\textstyle Pr\{{\text{x}}=x||\rho \}=Tr[\Im _{A}(x)\rho ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/586d4e469a1b620c551892a44aab492958653f02)


![{\textstyle Pr\{{\text{A}}=x||\rho \}=Tr[{\widehat {D}}^{A}(x)\rho ]=Tr[{\widehat {E}}^{A}(x)\rho ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9a8550566f3459e7cddbf180fcde8f50d4c299b)




![{\textstyle \rho \rightarrow \rho _{({\text{A}}=x)}={\frac {{V}(x)\rho V(x)^{*}}{Tr[{V}(x)\rho V(x)^{*}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba54c1d316d7ab6acff66de4f7dc854ac7eda6f0)




























![{\displaystyle Pr\{A=x\|\rho \}=Tr[{\Bigl (}I\otimes E^{M}{^{_{A}}(x){\Bigr )}}U(\rho \otimes \sigma )U^{*}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f3cd4375be3c41ac3dd1be33638372ab6f99ec1)



![{\displaystyle {\mathcal {P}}_{A}(x)\rho =Tr_{\mathcal {H}}[{\Bigl (}I\otimes E^{M}{^{_{A}}(x){\Bigr )}}U(\rho \otimes \sigma )U^{*}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/30510a056cd9495c058447715652efe281343aee)












![{\displaystyle [{\widehat {A}},{\widehat {B}}]\neq 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e9db6c1b5e87d54bf434dd1a9c5e27aec96f01b)



![{\displaystyle [{\mathcal {J_{A}(x)}},{\mathcal {J_{B}(x)}}]={\mathcal {J_{A}(x)}}{\mathcal {J_{B}(x)}}-{\mathcal {J_{B}(x)}},{\mathcal {J_{A}(x)}}\neq 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/361fd78b0a02b9327edd624db3524e24db18c76b)

![{\displaystyle \rho ,[\Im _{A}(x),\Im _{B}(x)]\rho =0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e92482fee8da2743e673c367d456a5072ea1ade)
![{\displaystyle [\Im _{A}(x),\Im _{B}(x)]\neq 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f79e1311a59bf9e0fb79419b798b7ed5b018f921)






















![{\displaystyle {\tfrac {d{\widehat {R}}}{dt}}(t)=-i[{\widehat {H}},{\widehat {R}},(t)],{\widehat {R}}(0)={\widehat {R}}_{0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5360ff03d80449ad8d6c2745e7b1ce43093e52c)



![{\displaystyle {\tfrac {d{\widehat {\rho }}}{dt}}(t)=-i[{\widehat {H}},{\widehat {\rho }},(t)]+{\widehat {L}}[{\widehat {\rho }}(t),{\widehat {\rho }}(0)={\widehat {\rho }}_{0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ced507a031874df17864ed03824140ff695bf48)















![{\displaystyle i[{\widehat {H}},{\widehat {\rho }}_{steady}]={\widehat {L}}[{\widehat {\rho }}_{steady}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f2a348496cb945fd0a1351418b60d74ad83430c)





























































































