Store:LTcondilo

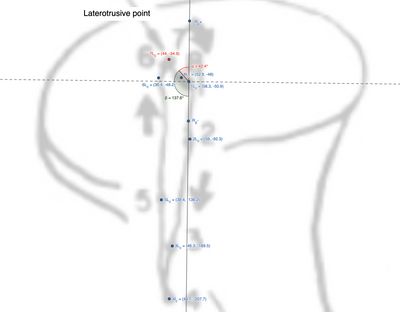
Condilo Laterotrusivo

Questo paragrafo illustra un processo matematico per calcolare la distanza e l'angolo formato tra due segmenti in un piano 2D, con applicazione nella cinematica mandibolare. La spiegazione riguarda il calcolo degli angoli tra vettori che rappresentano movimenti articolari, ad esempio i condili durante i movimenti mandibolari (Figura 2 e Tabella 1).

**Tabella 1: Distanze e direzioni**
**Tracciato masticatorio**	**Markers**	**Distanza (mm)**	**Direzione (X - antero-posteriore)**	**Direzione dinamica (Y - latero-mediale)**
	2	1.74	Nessuno	Lateralizzazione
	3	5.19	Avanti	Lateralizzazione
	4	6.96	Avanti	Lateralizzazione
	5	3.90	Indietro	Medializzazione
	6	0.99	Indietro	Medializzazione
	7*	1.32	Indietro	Medializzazione
	8	0.44	Indietro	Medializzazione

Osservando la figura e la tabella, possiamo estrapolare le distanze tra i punti marcati. Ad esempio, la distanza tra il punto $1_{L}$ e il punto $7_{L}$ è stata correttamente calcolata come circa $1.32_{\text{mm}}$ con una direzione calcolata come:

$\theta =42^{\circ }$

Per chi desidera approfondire il formalismo matematico, riportiamo il calcolo dettagliato nel popup interattivo.  Calcolo dettagliato della distanza e dell'angolo: dobbiamo calcolare la distanza euclidea tra i punti $P_{1}=(58.3,-50.9)$ e $P_{7}=(44,-34.9)$. La formula per la distanza euclidea è ${\text{distanza}}={\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}}$. Sostituendo i valori: ${\text{distanza}}={\sqrt {(44-58.3)^{2}+(-34.9-(-50.9))^{2}}}={\sqrt {(-14.3)^{2}+(16)^{2}}}={\sqrt {204.49+256}}={\sqrt {460.49}}\approx 21.47\,{\text{pixel}}$. A questo punto, per convertire in millimetri, moltiplichiamo la distanza per il fattore di scala: ${\text{distanza in mm}}=21.47\times 0.0418\approx 1.32\,{\text{mm}}$. Ora calcoliamo l'angolo $\theta$ utilizzando la formula per il coseno: $\cos(\theta )={\frac {{\vec {AB}}\cdot {\vec {AC}}}{|{\vec {AB}}|\cdot |{\vec {AC}}|}}$. Considerando i vettori e i calcoli, otteniamo $\cos(\theta )=0.789\implies \theta =42^{\circ }\,({\text{arrotondato}})$.