Quantenähnliche Modellierung in der Biologie mit offenen Quantensystemen und Instrumenten
| Title | Quantenähnliche Modellierung in der Biologie mit offenen Quantensystemen und Instrumenten |
| Authors | Irina Basieva · Andrei Khrennikov · Masanao Ozawa |
| Source | Document |
| Date | 2021 |
| Journal | Biosystems |
| DOI | 10.1016/j.biosystems.2020.104328 |
| PUBMED | https://pubmed.ncbi.nlm.nih.gov/33347968/ |
| PDF copy | |
| License | CC BY |
| This resource has been identified as a Free Scientific Resource, this is why Masticationpedia presents it here as a mean of gratitude toward the Authors, with appreciation for their choice of releasing it open to anyone's access | |
This is free scientific content. It has been released with a free license, this is why we can present it here now, for your convenience. Free knowledge, free access to scientific knowledge is a right of yours; it helps Science to grow, it helps you to have access to Science
This content was relased with a 'CC BY' license.
You might perhaps wish to thank the Author/s
Irina Basievaa, Andrei Khrennikova, Masanao Ozawab,c
aLinnaeus University, International Center for Mathematical Modeling in Physics and Cognitive Sciences Växjö, SE-351 95, Sweden
bCollege of Engineering, Chubu University, 1200 Matsumoto-cho, Kasugai 487-8501, Japan
cGraduate School of Informatics, Nagoya University, Chikusa-ku, Nagoya 464-8601, Japan
Abstrakt
Wir stellen den neuartigen Ansatz zur mathematischen Modellierung von Informationsprozessen in Biosystemen vor. Es untersucht den mathematischen Formalismus und die Methodik der Quantentheorie, insbesondere der Quantenmesstheorie. Dieser Ansatz ist als quantenähnlich bekannt und sollte von der Untersuchung echter quantenphysikalischer Prozesse in Biosystemen (Quantenbiophysik, Quantenkognition) unterschieden werden. Es basiert auf der Quanteninformationsdarstellung des Zustands des Biosystems und der Modellierung seiner Dynamik im Rahmen der Theorie offener Quantensysteme. Dieser Beitrag beginnt mit der nicht physikerfreundlichen Darstellung der Quantenmesstheorie, von der ursprünglichen von Neumann-Formulierung bis zur modernen Theorie der Quanteninstrumente. Letzteres wird dann auf Modellkombinationen von kognitiven Effekten und Genregulation des Glukose-/Laktosestoffwechsels im Escherichia coli-Bakterium angewendet. Die allgemeinste Konstruktion von Quanteninstrumenten basiert auf dem Schema der indirekten Messung, indem Messgeräte die Rolle der Umgebung für ein Biosystem spielen. Die biologische Essenz dieses Schemas wird durch die Quantenformalisierung der Helmholtz-Empfindungs-Wahrnehmungs-Theorie veranschaulicht. Dann gehen wir zur Dynamik offener Systeme über und betrachten die Quanten-Master-Gleichung, wobei wir uns auf Quanten-Markov-Prozesse konzentrieren. In diesem Rahmen modellieren wir das Funktionieren biologischer Funktionen wie psychologische Funktionen und epigenetische Mutationen.
Schlüsselwörter
Mathematischer Formalismus der Quantenmechanik, Offene Quantensysteme, Quanteninstrumente, Quanten-Markov-Dynamik, Genregulation, Psychologische Effekte, Kognition, Epigenetische Mutation, Biologische Funktionen
Einführung
Die mathematischen Standardmethoden wurden ursprünglich entwickelt, um der klassischen Physik zu dienen. Die Realanalyse diente als mathematische Grundlage der Newtonschen Mechanik (Newton, 1687)[1] (und später des Hamiltonschen Formalismus); die klassische statistische Mechanik stimulierte den maßtheoretischen Ansatz der Wahrscheinlichkeitstheorie, formalisiert in Kolmogorovs Axiomatik (Kolmogorov, 1933)[2]. Das Verhalten biologischer Systeme unterscheidet sich jedoch wesentlich vom Verhalten mechanischer Systeme, etwa starrer Körper, Gasmoleküle oder Flüssigkeiten. Obwohl die „klassische Mathematik“ immer noch die entscheidende Rolle bei der biologischen Modellierung spielt, scheint sie daher die reiche Komplexität von Biosystemen und Besonderheiten ihres Verhaltens – im Vergleich zu mechanischen Systemen – nicht vollständig beschreiben zu können. Neue mathematische Methoden zur Modellierung von Biosystemen sind gefragt.(a,b)
In diesem Artikel stellen wir die Anwendungen des mathematischen Formalismus der Quantenmechanik und seiner Methodik zur Modellierung des Verhaltens von Biosystemen vor.(c) Die letzten Jahre waren gekennzeichnet durch eine Explosion des Interesses an Anwendungen der Quantentheorie außerhalb der Physik, insbesondere in der kognitiven Psychologie, Entscheidungsfindung, Informationsverarbeitung im Gehirn, Molekularbiologie, Genetik und Epigenetik und Evolutionstheorie.4 Wir nennen die entsprechenden Modelle quantenartig. Sie zielen nicht auf die Mikromodellierung echter quantenphysikalischer Prozesse in Biosystemen ab, etwa in Zellen oder Gehirnen (vgl. zu biologischen Anwendungen echter quantenphysikalischer Theorie Penrose 1989[3], Umezawa 1993[4], Hameroff 1994[5], Vitiello 1995[6], Vitiello 2001[7], Arndt et al., 2009[8], Bernroider und Summhammer 2012[9], Bernroider 2017[10]). Quantenähnliche Modellierung arbeitet aus Sicht der Quantentheorie als Messtheorie. Dies ist der ursprüngliche Standpunkt Bohrs, der zur Kopenhagener Interpretation der Quantenmechanik führte (siehe Plotnitsky, 2009[11] für eine detaillierte und klare Darstellung von Bohrs Ansichten). Eine der wichtigsten Bio-Spezialitäten ist die Berücksichtigung von Selbstmessungen, die Biosysteme an sich selbst durchführen. In unserer Modellierung wird die Fähigkeit zur Durchführung von Selbstmessungen als grundlegendes Merkmal biologischer Funktionen betrachtet (siehe Abschnitt 8.2 und Artikel Khrennikov et al., 2018[12]).
Quantenähnliche Modelle (Khrennikov, 2004b[13]) spiegeln die Merkmale biologischer Prozesse wider, die natürlicherweise mit dem Quantenformalismus übereinstimmen. Bei einer solchen Modellierung ist es nützlich, die Quanteninformationstheorie zu untersuchen, die nicht nur auf die Mikrowelt der Quantensysteme angewendet werden kann. Im Allgemeinen müssen Systeme, die Informationen auf quantenähnliche Weise verarbeiten, keine quantenphysikalischen Systeme sein; insbesondere können sie makroskopische Biosysteme sein. Überraschenderweise kann dieselbe mathematische Theorie auf allen biologischen Ebenen angewendet werden: von Proteinen, Zellen und Gehirnen bis hin zu Menschen und Ökosystemen; wir können von Quanteninformationsbiologie sprechen (Asano et al., 2015a[14]).
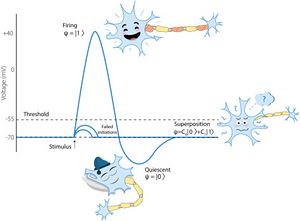
In der quantenähnlichen Modellierung wird die Quantentheorie als Kalkül zur Vorhersage und Transformation von Wahrscheinlichkeiten betrachtet. Die Quantenwahrscheinlichkeitsrechnung (QP) (Abschnitt 2) unterscheidet sich wesentlich von der klassischen Wahrscheinlichkeitsrechnung (CP), die auf Kolmogorovs Axiomatik basiert (Kolmogorov, 1933[15]). In CP werden Zustände von Zufallssystemen durch Wahrscheinlichkeitsmaße und Observables durch Zufallsvariablen dargestellt; in QP werden Zustände zufälliger Systeme durch normalisierte Vektoren in einem komplexen Hilbert-Raum (reine Zustände) oder allgemein durch Dichteoperatoren (gemischte Zustände) dargestellt.5 Superpositionen, die durch reine Zustände dargestellt werden, werden verwendet, um Unsicherheiten zu modellieren, die noch nicht durch eine Messung aufgelöst wurden. Die Verwendung von Überlagerungen in der Biologie wird durch Abb. 1 veranschaulicht (siehe Abschnitt 10 und Artikel Khrennikov et al., 2018[12] für das entsprechende Modell). Das aus einer Beobachtung resultierende QP-Update basiert auf dem Projektionspostulat oder allgemeineren Transformationen von Quantenzuständen – im Rahmen der Theorie von Quanteninstrumenten (Davies und Lewis, 1970[16], Davies, 1976[17], Ozawa, 1984[18], Yuen, 1987[19], Ozawa , 1997[20], Ozawa, 2004[21], Okamura und Ozawa, 2016[22]) (Abschnitt 3).
Wir betonen, dass die quantenähnliche Modellierung die Rolle der Bequemlichkeit und Einfachheit der Quantendarstellung von Zuständen und Observablen erhöht. (Wir ignorieren pragmatisch das Problem der Wechselbeziehung von CP und QP.) Insbesondere hat der Quantenzustandsraum die lineare Struktur und lineare Modelle sind einfacher. Der Übergang von der klassischen nichtlinearen Dynamik elektrochemischer Prozesse in Biosystemen zur quantenlinearen Dynamik beschleunigt wesentlich die Zustandsentwicklung (Abschnitt 8.4). In diesem Rahmen ist „Zustand“ jedoch der Quanteninformationszustand eines Biosystems, der zur Verarbeitung spezieller Quantenunsicherheit verwendet wird (Abschnitt 8.2).
Beobachtungen
In Lehrbüchern zur Quantenmechanik wird häufig darauf hingewiesen, dass das Hauptunterscheidungsmerkmal der Quantentheorie das Vorhandensein inkompatibler Observablen ist. Wir erinnern uns an diese zwei Observablen 𝐴 𝐵 und sind inkompatibel, wenn es unmöglich ist, ihnen gemeinsam Werte zuzuordnen. Im probabilistischen Modell führt dies dazu, dass es unmöglich ist, ihre gemeinsame Wahrscheinlichkeitsverteilung (JPD) zu bestimmen. Die grundlegenden Beispiele für inkompatible Observable sind Position und Impuls eines Quantensystems oder Spin- (oder Polarisations-) Projektionen auf verschiedene Achsen. Im mathematischen Formalismus wird Inkompatibilität als Nichtkommutativität hermitescher Operatoren beschrieben Und Observablen darstellen, d.h.
Hier beziehen wir uns auf das ursprüngliche und immer noch grundlegende und weit verbreitete Modell der Quantenobservablen, Von Neumann 1955[23] (Abschnitt 3.2).
Inkompatibilitäts-Nichtkommutativität wird in der Quantenphysik häufig verwendet, und die grundlegenden physikalischen Observablen, wie beispielsweise Position und Impuls, Spin- und Polarisationsprojektionen, werden in diesem Paradigma traditionell durch hermitische Operatoren dargestellt. Wir weisen auch auf zahlreiche Anwendungen dieses Ansatzes in den Bereichen Kognition, Psychologie und Entscheidungsfindung hin (Khrennikov, 2004a[24], Busemeyer und Bruza, 2012[25], Bagarello, 2019[26]) (siehe insbesondere Artikel (Bagarello et al., 2018[27]), der sich der Quantifizierung der Heisenbergsche Unsicherheitsrelationen bei der Entscheidungsfindung). Dennoch mag es für unseren Zweck nicht allgemein genug sein – für die quantenähnliche Modellierung in der Biologie kann nicht jede Art von nicht-klassischer Biostatistik einfach an das von Neumann-Beobachtungsmodell delegiert werden. Beispielsweise können selbst sehr grundlegende kognitive Effekte nicht konsistent mit dem Standardbeobachtungsmodell beschrieben werden (Khrennikov et al., 2014[28], Basieva und Khrennikov, 2015[29]).
Wir werden eine allgemeinere Theorie der Beobachtungen auf der Grundlage von Quanteninstrumenten untersuchen (Davies und Lewis, 1970[16], Davies, 1976[17], Ozawa, 1984[18], Yuen, 1987[19], Ozawa, 1997[20], Ozawa, 2004[21], Okamura und Ozawa, 2016[22]) und nützliche Werkzeuge dafür finden Anwendungen zur Modellierung kognitiver Effekte (Ozawa und Khrennikov, 2020a[30], Ozawa und Khrennikov, 2020b[31]). Wir werden diese Frage in Abschnitt 3 diskutieren und in den Abschnitten 6, 7 mit Beispielen aus der Kognitions- und Molekularbiologie veranschaulichen. Im Rahmen der Quanteninstrumententheorie ist der entscheidende Punkt nicht die Kommutativität vs. Nichtkommutativität von Operatoren, die Observablen symbolisch darstellen, sondern die mathematische Form der Zustandstransformation, die sich aus der Rückwirkung der (Selbst-)Beobachtung ergibt. Im Standardansatz wird diese Transformation durch eine orthogonale Projektion auf den Unterraum von Eigenvektoren gegeben, die der Ausgabe der Beobachtung entsprechen. Dies ist das Projektionspostulat. In der Quanteninstrumententheorie sind Zustandstransformationen allgemeiner.
Die Berechnung von Quanteninstrumenten ist eng gekoppelt mit der Theorie offener Quantensysteme (Ingarden et al., 1997[32]), Quantensysteme, die mit Umgebungen interagieren. Wir bemerken, dass quantenphysikalische Systeme in manchen Situationen als (zumindest annähernd) isoliert betrachtet werden können. Biosysteme sind jedoch grundsätzlich offen. Wie von Schrödinger (1944[33]) betont wurde, ist ein vollständig isoliertes Biosystem tot. Letzteres erklärt, warum die Theorie offener Quantensysteme und insbesondere der Quanteninstrumentenkalkül als mathematischer Apparat der Quanteninformationsbiologie die grundlegende Rolle in Anwendungen in der Biologie spielen (Asano et al., 2015a[14]).
Innerhalb der Theorie offener Quantensysteme modellieren wir die epigenetische Evolution (Asano et al., 2012b[34], Asano et al., 2015b[35]) (Abschnitte 9, 11.2) und die Leistung psychologischer (kognitiver) Funktionen, die vom Gehirn realisiert werden (Asano et al., 2011[36], Asano et al., 2015b[35], Khrennikov et al., 2018[12]) (Abschnitte 10, 11.3).
Für mathematisch ausreichend gut ausgebildete Biologen, aber ohne Kenntnisse in Physik, können wir das Buch (Khrennikov, 2016a[37]) empfehlen, das die Präsentationen von CP und QP mit einer kurzen Einführung in den Quantenformalismus kombiniert, einschließlich der Theorie von Quanteninstrumenten und bedingten Wahrscheinlichkeiten
2. Klassische versus Quantenwahrscheinlichkeit
CP wurde von Kolmogorov (1933)[15] mathematisch formalisiert. Dies ist die Wahrscheinlichkeitsrechnung, bei der ein nicht negatives Gewicht
ist jedem Ereignis zugeordnet . Die Haupteigenschaft von CP ist seine Additivität: wenn zwei Ereignisse disjunkt sind, dann ist die Wahrscheinlichkeit der Disjunktion dieser Ereignisse gleich der Summe der Wahrscheinlichkeiten:
QP ist das Kalkül komplexer Amplituden oder im abstrakten Formalismus komplexer Vektoren. Anstelle von Operationen auf Wahrscheinlichkeitsmaßen wird also mit Vektoren operiert. Wir können sagen, dass QP ein Vektormodell des probabilistischen Denkens ist. Jede komplexe Amplitude gibt die Wahrscheinlichkeit nach der Bornschen Regel an: Die Wahrscheinlichkeit erhält man als Quadrat des Betrags der komplexen Amplitude.
(zur Formalisierung des Hilbert-Raums siehe Abschnitt 3.2, Formel (7)). Durch das Arbeiten mit komplexen Wahrscheinlichkeitsamplituden anstelle des direkten Arbeitens mit Wahrscheinlichkeiten kann man die Grundgesetze von CP verletzen.
In CP wird die Formel der Gesamtwahrscheinlichkeit (FTP) unter Verwendung der Additivität der Wahrscheinlichkeit und der Bayes-Formel, der Definition der bedingten Wahrscheinlichkeit, abgeleitet, ,
Betrachten Sie das Paar, und , diskreter klassischer Zufallsvariablen. Dann
Thus, in CP the -probability distribution can be calculated from the -probability and the conditional probabilities
So ist in CP die -Wahrscheinlichkeitsverteilung kann aus der berechnet werden -Wahrscheinlichkeit und die bedingten Wahrscheinlichkeiten
In QP, classical FTP is perturbed by the interference term (Khrennikov, 2010); for dichotomous quantum observables and of the von Neumann-type, i.e., given by Hermitian operators and , the quantum version of FTP has the form:
Bei QP wird klassisches FTP durch den Interferenzterm gestört (Khrennikov, 2010[38]); für dichotome Quantenobservablen Und vom von-Neumann-Typ, d.h. gegeben durch hermitesche Operatoren Und , hat die Quantenversion von FTP die Form:
Wenn der Interferenzterm7 positiv ist, dann würde der QP-Kalkül eine Wahrscheinlichkeit erzeugen, die größer ist als sein CP-Gegenstück, das durch die klassische FTP gegeben ist (2). Insbesondere diese Wahrscheinlichkeitsverstärkung ist die Grundlage der Vormachtstellung des Quantencomputings.
Es gibt eine Fülle statistischer Daten aus der kognitiven Psychologie, Entscheidungsfindung, Molekularbiologie, Genetik und Epigenetik, die zeigen, dass Biosysteme, von Proteinen und Zellen (Asano et al., 2015b[35]) bis hin zum Menschen (Khrennikov, 2010[39], Busemeyer und Bruza, 2012[25]) nutzen diese Verstärkung und arbeiten mit Nicht-CP-Updates. Wir setzen unsere Präsentation mit solchen Beispielen fort. \
3. Quanteninstrumente
3.1. Ein paar Worte zum Quantenformalismus
Bezeichne mit ein komplexer Hilbertraum. Der Einfachheit halber nehmen wir an, dass es endlichdimensional ist. Reine Zustände eines Systems sind durch normalisierte Vektoren von gegeben und gemischte Zustände durch Dichteoperatoren (positive semidefinite Operatoren mit Einheitsspur). Der Raum der Dichteoperatoren wird mit bezeichnet (). Der Raum aller linearen Operatoren in wird durch das Symbol gekennzeichnet . Dies wiederum ist ein linearer Raum. Darüber hinaus ist der komplexe Hilbert-Raum mit dem Skalarprodukt, . Wir betrachten lineare Operatoren, die einwirken. Sie werden Superoperatoren genannt.
Die Dynamik des reinen Zustands eines isolierten Quantensystems wird durch die Schrödinger-Gleichung beschrieben:
Wo ist der Hamiltonoperator des Systems. Diese Gleichung impliziert, dass der reine Zustand entwickelt sich einheitlich , Wo ist eine parametrische Gruppe von unitären Operatoren, . In der Quantenphysik Hamiltonian ist mit dem Energie-Beobachtbaren verbunden. Die gleiche Interpretation wird in der Quantenbiophysik verwendet (Arndt et al., 2009). In unserer quantenähnlichen Modellierung, die die Informationsverarbeitung in Biosystemen beschreibt, jedoch der Operator hat keine direkte Kopplung mit physikalischer Energie. Dies ist der Evolutionsgenerator, der Informationsinteraktionen beschreibt.
Dynamik für einen reinen Zustand impliziert, dass die Dynamik eines gemischten Zustands (dargestellt durch einen Dichteoperator) durch die von Neumann-Gleichung beschrieben wird:
3.2. Von Neumann-Formalismus für Quantenobservablen
Im ursprünglichen Quantenformalismus (Von Neumann, 1955) physikalisch beobachtbar wird durch einen hermiteschen Operator dargestellt . Wir betrachten nur Operatoren mit diskreten Spektren: Wo ist der Projektor auf den Unterraum von entspricht dem Eigenwert . Angenommen, der Zustand des Systems wird mathematisch durch einen Dichteoperator dargestellt . Dann die Wahrscheinlichkeit, die Antwort zu bekommen ist durch die Born-Regel gegeben
und nach dem Projektionspostulat erhält man den Zustand nach der Messung über die Zustandstransformation:
Der Einfachheit halber präsentieren wir diese Formeln für einen reinen Anfangszustand . Die Bornsche Regel hat die Form:
Die Zustandstransformation ist durch das Projektionspostulat gegeben:
Hier der Observable-Operator (seine spektrale Zerlegung) bestimmt eindeutig die Rückkopplungszustandstransformationen für Ergebnisse
Die Karte gegeben durch (9) ist das einfachste (aber sehr wichtige) Beispiel eines Quanteninstruments.
3.3. Nicht-projektive Zustandsaktualisierung: atomare Instrumente
Im Allgemeinen werden die statistischen Eigenschaften jeder Messung dadurch gekennzeichnet
- die Ausgabewahrscheinlichkeitsverteilung , die Wahrscheinlichkeitsverteilung der Ausgabe der Messung im Eingangszustand
- die Quantenzustandsreduktion , die Zustandsänderung vom Eingangszustand zum Ausgangszustand abhängig vom Ergebnis der Messung.
In von Neumann’s formulation, the statistical properties of any measurement of an observable is uniquely determined by Born’s rule (5) and the projection postulate (6), and they are represented by the map (9), an instrument of von Neumann type. However, von Neumann’s formulation does not reflect the fact that the same observable represented by the Hermitian operator in can be measured in many ways.8 Formally, such measurement-schemes are represented by quantum instruments.
In von Neumanns Formulierung werden die statistischen Eigenschaften jeder Messung einer Observablen eindeutig durch die Bornsche Regel (5) und das Projektionspostulat (6) bestimmt, und sie werden durch die Karte (9), ein Instrument vom Typ von Neumann, dargestellt. Die Formulierung von von Neumann spiegelt jedoch nicht die Tatsache wider, dass dieselbe Observable dargestellt durch den hermiteschen Operator In kann auf vielfältige Weise gemessen werden.8 Formal werden solche Messschemata durch Quanteninstrumente repräsentiert.
Wir betrachten die einfachsten Quanteninstrumente vom Nicht-von-Neumann-Typ, die als atomare Instrumente bekannt sind. Wir beginnen mit der Erinnerung an den Begriff POVM (Probability Operator Valued Measure); wir beschränken Betrachtungen auf POVMs mit einem diskreten Definitionsbereich . POVM ist eine Karte so dass für jeden , ist ein positiver kontraktiver hermitescher Operator (Effekt genannt) (d. h. oder irgendein , ) und die Normalisierungsbedingung
hält, wo ist der Einheitsoperator. Es wird davon ausgegangen, dass für jede Messung die Wahrscheinlichkeitsverteilung ausgegeben wird
wird von gegeben
Wo ist ein POVM. Bei atomaren Instrumenten wird davon ausgegangen, dass Wirkungen konkret in der Form dargestellt werden
Wo ist ein linearer Operator in . Die Normierungsbedingung hat also die Form .9 Die Born-Regel kann ähnlich wie (5) geschrieben werden:
Es wird angenommen, dass die Zustandstransformation nach der Messung auf der Karte basiert:
| * |
die Quantenzustandsreduktion ist also gegeben durch
| * |
Die Karte gegeben durch (13) ist ein atomares Quanteninstrument. Wir bemerken, dass die Born-Regel (12) in der Form geschrieben werden kann
| * | f |
Lassen sei ein hermitescher Operator in . Betrachten Sie eine POVM mit dem Definitionsbereich, der durch das Spektrum von gegeben ist . Dieses POVM repräsentiert eine Messung von Observable wenn die Bornsche Regel gilt:
Somit sind im Prinzip Ergebniswahrscheinlichkeiten immer noch in der spektralen Zerlegung von Operatoren kodiert oder mit anderen Worten Operatoren sollten so gewählt werden, dass sie die Wahrscheinlichkeiten erzeugen, die der spektralen Zerlegung der symbolischen Darstellung entsprechen von Observablen , d. h., ist eindeutig bestimmt durch als . Wir können sagen, dass dieser Operator im Gegensatz zum Operator des von Neumann-Schemas nur Informationen über die Wahrscheinlichkeiten von Ergebnissen enthält codiert nicht die Regel der Zustandsaktualisierung. Bei einem atomaren Instrument Messungen des Observablen hat die eindeutige Ausgabewahrscheinlichkeitsverteilung nach der Bornschen Regel (16), hat aber viele verschiedene Quantenzustandsreduktionen, abhängig von der Zerlegung des Effekts Sodass
3.4. Allgemeine Theorie (Davies–Lewis–Ozawa)
Schließlich formulieren wir den allgemeinen Begriff des Quanteninstruments. Ein Superoperator, der eingreift heißt positiv, wenn es die Menge der positiven semidefiniten Operatoren in sich selbst abbildet. Wir bemerken das für jeden gegeben durch (13) kann als lineare positive Abbildung betrachtet werden.
Im Allgemeinen jede Karte , wo für jeden , die Karte ein positiver Superoperator ist, wird Davies-Lewis-Quanteninstrument (Davies und Lewis, 1970) genannt.
Hier Index bezeichnet die an dieses Instrument gekoppelte Observable. Die Wahrscheinlichkeiten von -Ergebnisse sind durch die Bornsche Regel in Form (15) und die Zustandsaktualisierung durch Transformation (14) gegeben. Yuen (1987) wies jedoch darauf hin, dass die Klasse der Davies-Lewis-Instrumente zu allgemein ist, um physikalisch nicht realisierbare Instrumente auszuschließen. Ozawa (1984) führte die wichtige zusätzliche Bedingung ein, um sicherzustellen, dass jedes Quanteninstrument physikalisch realisierbar ist. Dies ist die Bedingung vollständiger Positivität.
Ein Superoperator heißt vollständig positiv, wenn seine natürliche Erweiterung zum Tensorprodukt liegt wieder ein positiver Superoperator an . Eine Karte , wo für jeden , die Karte ein vollständig positiver Superoperator ist, heißt Davies-Lewis-Ozawa (Davies und Lewis, 1970, Ozawa, 1984) Quanteninstrument oder einfach Quanteninstrument. Wie wir in Abschnitt 4 sehen werden, ist vollständige Positivität eine hinreichende Bedingung dafür, dass ein Instrument physikalisch realisierbar ist. Andererseits wird die Notwendigkeit wie folgt hergeleitet (Ozawa, 2004).
Alles beobachtbar eines Systems wird mit dem Beobachtbaren identifiziert eines Systems mit jedem System extern zu .10
Dann jedes physikalisch realisierbare Instrument messung sollte mit dem Instrument identifiziert werden messung so dass . Dies impliziert das ist wieder ein positiver Superoperator, so dass ist absolut positiv.
Ebenso jedes physikalisch realisierbare Instrument Messsystem sollte sein erweitertes Instrument haben Messsystem für jedes externe System. Dies ist nur dann erfüllt, wenn ist absolut positiv. Daher ist vollständige Positivität eine notwendige Bedingung für ein physikalisch realisierbares Instrument zu beschreiben.
4. Quanteninstrumente aus dem Schema der indirekten Messungen
Das Grundmodell für den Bau von Quanteninstrumenten basiert auf dem Schema indirekter Messungen. Dieses Schema formalisiert die folgende Situation: Die Ergebnisse der Messung werden durch die Interaktion eines Systems generiert mit einem Messgerät .Dieser Apparat besteht aus einem komplexen physikalischen Gerät, das mit ihm interagiert und einen Zeiger, der das Ergebnis der Messung anzeigt, sagen wir Spin up oder Spin down. Ein Beobachter kann nur Ausgaben des Zeigers sehen und er ordnet diese Ausgaben den Werten der Observablen zu für das System . Somit beinhaltet das indirekte Messschema:
- die Zustände der Systeme und der Apparat
- der Betreiber die Interaktionsdynamik für das System darstellt
- das Messgerät beobachtbar Ausgabe des Zeigers der Vorrichtung.
Ein indirektes Messmodell, eingeführt in Ozawa (1984) als „(allgemeiner) Messprozess“, ist ein Quadrupel
bestehend aus einem Hilbertraum , ein Dichteoperator , ein einheitlicher Operator auf dem Tensorprodukt der Zustandsräume von and und ein hermitescher Operator on .Durch dieses Messmodell entsteht der Hilbert-Raum beschreibt die Zustände des Geräts ,der Einheitsoperator beschreibt die zeitliche Entwicklung des zusammengesetzten Systems ,der Dichteoperator beschreibt den Ausgangszustand des Gerätes , und der hermitesche Operator beschreibt die vom Gerät beobachtbare Messgröße . Dann die ausgegebene Wahrscheinlichkeitsverteilung im Systemzustand wird von gegeben
Wo ist die spektrale Projektion von für den Eigenwert .
Der Zustandswechsel vom System verursacht durch die Messung für das Ergebnis wird mit Hilfe der Karte dargestellt im Raum der Dichteoperatoren definiert als
Wo ist die Teilspur vorbei . Dann die Karte entpuppt sich als Quanteninstrument. Somit werden die statistischen Eigenschaften der Messung durch jedes indirekte Messmodell realisiert wird durch eine Quantenmessung beschrieben. Wir bemerken, dass umgekehrt jedes Quanteninstrument durch das indirekte Messmodell (Ozawa, 1984) dargestellt werden kann. Quanteninstrumente charakterisieren also mathematisch die statistischen Eigenschaften aller physikalisch realisierbaren Quantenmessungen.
5. Modellierung des Empfindungs-Wahrnehmungsprozesses im Rahmen des indirekten Messschemas
Die Grundlagen der Theorie des unbewussten Schließens für die Bildung visueller Eindrücke wurden im 19. Jahrhundert von H. von Helmholtz gelegt. Obwohl von Helmholtz hauptsächlich die visuelle Wahrnehmung untersuchte, wendete er seine Theorie auch auf andere Sinne an, bis er in der Theorie der sozialen unbewussten Schlussfolgerung gipfelte. Von Helmholtz hier sind zwei Stadien des kognitiven Prozesses, und sie unterscheiden zwischen Empfindung und Wahrnehmung wie folgt:
- Empfindung ist ein Signal, das das Gehirn als Ton oder visuelles Bild usw. interpretiert.
- Wahrnehmung ist etwas, das als Präferenz oder selektive Aufmerksamkeit usw.
Im Schema der indirekten Messung stellen Empfindungen die Zustände des Empfindungssystems des Menschen dar und das Wahrnehmungssystem spielt die Rolle des Messgeräts. Der Einheitsoperator beschreibt den Interaktionsprozess zwischen den Empfindungs- und Wahrnehmungszuständen. Diese Quantenmodellierung des Empfindungs-Wahrnehmungsprozesses wurde in einem Artikel (Khrennikov, 2015) mit Anwendung auf bistabile Wahrnehmung und experimentelle Daten aus dem Artikel (Asano et al., 2014) vorgestellt.
6. Modellierung kognitiver Effekte
In der Kognitions- und Sozialwissenschaft ist folgender Meinungspool als grundlegendes Beispiel für den Ordnungseffekt bekannt. Dies ist der Meinungspool von Clinton und Gore (Moore, 2002). In diesem Experiment wurde amerikanischen Bürgern jeweils eine Frage gestellt, z. B.
- „Ist Bill Clinton ehrlich und vertrauenswürdig?“
- „Ist Al Gore ehrlich und vertrauenswürdig?“
Auf der Grundlage der experimentellen statistischen Daten wurden zwei aufeinanderfolgende Wahrscheinlichkeitsverteilungen berechnet, Und (erste Frage und dann fragen und umgekehrt).
6.1.Ordnungseffekt bei sequentieller Befragung
Die statistischen Daten aus diesem Experiment zeigten den Effekt der Fragereihenfolge QOE, Abhängigkeit der sequentiellen gemeinsamen Wahrscheinlichkeitsverteilung für Antworten auf die Fragen von ihrer Reihenfolge . Wir bemerken, dass im CP-Modell diese Wahrscheinlichkeitsverteilungen zusammenfallen:
Wo ist ein Musterraum und ist ein Wahrscheinlichkeitsmaß.
QOE stimuliert die Anwendung des QP-Kalküls auf Kognition, siehe Artikel (Wang und Busemeyer, 2013). Die Autoren dieses Artikels betonten, dass das nichtkommutative Merkmal gemeinsamer Wahrscheinlichkeiten modelliert werden kann, indem die Nichtkommutativität von inkompatiblen Quantenobservablen verwendet wird dargestellt durch hermitesche Operatoren . Beobachtbar stellt die Clinton-Frage dar und ist beobachtbar stellt die Gore-Frage dar. In diesem Modell ist QOE identische Inkompatibilität – Nichtkommutativität von Observablen:
6.2.Antwortreplizierbarkeitseffekt für sequentielle Befragung
Der Ansatz basiert auf der Identifizierung des Ordnungseffekts mit nichtkommutativer Repräsentation von Fragen (Wang und Busemeyer, 2013)[40] wurde in Papieren kritisiert (Khrennikov et al., 2014).[12]Um dieses Papier zu diskutieren, erinnern wir uns an den Begriff der Antwortreplizierbarkeit. Angenommen, einer Person, sagen wir John, wird eine Frage gestellt und angenommen, er antwortet z. B. mit „ja“. Wird ihm unmittelbar danach dieselbe Frage noch einmal gestellt, so antwortet er mit Wahrscheinlichkeit eins „ja“. Wir nennen dies Eigenschaft Antwortreplizierbarkeit. In der Quantenphysik Response-Reproduzierbarkeit wird durch das Projektionspostulat ausgedrückt. Sowohl die Clinton-Gore-Meinungsumfrage als auch typische Experimente zur Entscheidungsfindung überzeugen Antwortreplizierbarkeit. Die Entscheidungsfindung hat noch ein weiteres Merkmal - Antwortreplizierbarkeit. Angenommen, nach der Beantwortung der -Frage mit „Ja“ beantworten, John wird eine weitere Frage gestellt . Er antwortete darauf mit einer Antwort. Und dann wird er gefragt nochmal. In dem oben erwähnten Social Opinion Pool wiederholt John ihre ursprüngliche Antwort auf ,„ja“ (mit Wahrscheinlichkeit eins).
Dieses Verhaltensphänomen nennen wir Antwortreplizierbarkeit. Kombination von mit und Response-Replizierbarkeit wird als Response-Replizierbarkeitseffekt RRE bezeichnet.
6.3. „QOE+RRE“: beschrieben durch Quanteninstrumente des nicht-projektiven Typs
Auf Papier (Khrennikov et al., 2014),[12] Es wurde gezeigt, dass es unter Verwendung des von Neumann-Kalküls unmöglich ist, RRE mit QOE zu kombinieren. Um QOE zu erzeugen, hermitische Operatoren sollte nichtkommutativ sein, aber letzteres zerstört Antwort Reproduzierbarkeit von .Dies war ein ziemlich unerwartetes Ergebnis. Es machte sogar den Eindruck, dass, obwohl die grundlegenden kognitiven Effekte quantenähnlich modelliert werden können, ihre Kombinationen nicht durch den Quantenformalismus beschrieben werden können.
Kürzlich wurde jedoch gezeigt, dass die Theorie der Quanteninstrumente eine einfache Lösung für die Kombination von QOE- und RRE-Effekten bietet, siehe Ozawa und Khrennikov (2020a)[41]für den Bau solcher Instrumente. Diese Instrumente sind vom nicht-projektiven Typ. Die Essenz von QOE liegt also nicht in der Struktur der Observablen, sondern in der Struktur der Zustandstransformation, die durch das Feedback der Messungen erzeugt wird. Bei QOE geht es nicht um die gemeinsame Messung und Inkompatibilität (Nichtkommutativität) von Observablen, sondern um sequentielle Messung von Observablen und sequentielle (Mental-)Zustandsaktualisierung. Quanteninstrumente, die in Ozawa und Khrennikov (2020a) verwendet werden[41] QOE und RRE zu kombinieren entspricht der Messung von Observablen, die durch pendelnde Operatoren repräsentiert werden . Darüber hinaus lässt sich nachweisen, dass QOE und RRE (unter natürlicher mathematischer Einschränkung) nur mit Hilfe von Quanteninstrumenten für kommutierende Observablen gemeinsam modelliert werden können.
6.4. Geistiger Realismus
Seit den Anfängen der Quantenmechanik Nichtkommutativität von Operatoren Beobachtungsgrößen darstellen was considered as the mathematical representation of their incompatibility. Philosophisch wird diese Situation als Unmöglichkeit der realistischen Beschreibung behandelt. In der Kognitionswissenschaft bedeutet dies, dass es mentale Zustände gibt, bei denen ein Individuum nicht beiden Observablen (z. B. Fragen) die eindeutigen Werte zuordnen kann. Die mathematische Beschreibung von QOE mit Observablen, die durch nichtkommutative Operatoren (im von Neumann-Schema) dargestellt werden, in Wang und Busemeyer (2013) und Wang et al. (2014) den Eindruck, dass dieser Effekt eine Ablehnung des mentalen Realismus impliziert. Das Ergebnis von Ozawa und Khrennikov (2020a) zeigt, dass trotz experimentell gut dokumentierter QOE der mentale Realismus nicht abgelehnt werden muss. QOE kann innerhalb des realistischen Bildes modelliert werden, das mathematisch durch die gemeinsame Wahrscheinlichkeitsverteilung von Observablen gegeben ist und , aber mit der nicht kommutativen Aktion von Quanteninstrumenten, die den mentalen Zustand aktualisieren:
Dies ist der richtige Ort, um zu bemerken, dass wenn für einen Staat , dann verschwindet QOE, auch wenn.Dies kann als die richtige Formulierung der Wang-Bussemeyer-Aussage zum Zusammenhang von QOE mit Nichtkommutativität angesehen werden. Statt Nichtkommutativität der Operatoren und Quantenobservable symbolisch darstellend, muss man von Nichtkommutativität entsprechender Quanteninstrumente sprechen.
7. Genetik: Eingriff in den Glukose-/Laktosestoffwechsel
In einer Veröffentlichung (Asano et al., 2012a) wurde ein quantenähnliches Modell entwickelt, das die Genregulation des Glukose-/Laktosestoffwechsels im Bakterium Escherichia coli beschreibt.11 Es gibt mehrere Arten von E. coli, die durch das Stoffwechselsystem charakterisiert sind. Es wurde gezeigt, dass die konkrete Art von E. coli durch die wohlbestimmten linearen Operatoren beschrieben werden kann; wir finden die unveränderlichen Operatorgrößen, die jeden Typ charakterisieren. Solche invarianten Operatorgrößen können aus den erhaltenen statistischen Daten berechnet werden. Also wurde die quantenähnliche Darstellung aus experimentellen Daten rekonstruiert.
Betrachten wir ein Ereignissystem bedeutet das Ereignis, dass E. coli sein Lactose-Operon aktiviert, das heißt, das Ereignis, dass &bgr;-Galactosidase durch die Transkription von mRNA von einem Gen im Lactose-Operon produziert wird; bedeutet das Ereignis, dass E. coli sein Lactose-Operon nicht aktiviert.
Dieses System von Ereignissen entspricht einer beobachtbaren Aktivierung, die mathematisch durch ein Quanteninstrument dargestellt wird . Betrachten Sie nun ein anderes System von Ereignissen wo bedeutet das Ereignis, dass ein E. coli-Bakterium ein Laktosemolekül in der Umgebung der Zelle erkennt, bedeutet Nachweis eines Glukosemoleküls. Dieses System von Ereignissen entspricht einer beobachtbaren Erkennung das durch ein Quanteninstrument dargestellt wird .
In diesem Modell wird die Interaktionsreaktion des Bakteriums mit der Glukose/Laktose-Umgebung als sequentielle Aktion von zwei Quanteninstrumenten beschrieben, zuerst Erkennung und dann Aktivierung. Wie in Asano et al. (2012a) können diese Quanteninstrumente für jede konkrete Art von E. coli-Bakterien aus den experimentellen Daten rekonstruiert werden; in Asanoet al. (2012a) wurde eine Rekonstruktion für das E. coli-Bakterium vom Typ W3110 durchgeführt. Das klassische FTP mit Observables and verletzt wird, wurde der Interferenzterm, siehe (2), berechnet (Asano et al., 2012a).
8.Offene Quantensysteme: Interaktion eines Biosystems mit seiner Umgebung
Wie bereits betont wurde, jedes Biosystem ist grundsätzlich offen. Daher muss die Dynamik seines Zustands über eine Wechselwirkung mit der Umgebung modelliert werden . Die Staaten von und sind in den Hilberträumen vertreten und . Das zusammengesetzte System wird im Tensorprodukt Hilberträume dargestellt. Dieses System wird als isoliertes System behandelt und gemäß der Quantentheorie kann die Dynamik seines reinen Zustands durch die Schrödinger-Gleichung beschrieben werden:
wo ist der reine Zustand des Systems and ist sein Hamiltonoperator. Diese Gleichung impliziert, dass der reine Zustand entwickelt sich einheitlich: . Here . Hamiltonian (Evolutionsgenerator), der Informationsinteraktionen beschreibt, hat die Form , wo ,sind Hamiltonoperatoren der Systeme und ist der Wechselwirkungs-Hamiltonoperator.12 Diese Gleichung impliziert, dass die Evolution des Dichteoperators of the system wird durch die von Neumann-Gleichung beschrieben:
Allerdings der Staat ist für jede mathematische Analyse zu komplex: Die Umgebung enthält zu viele Freiheitsgrade. Daher interessiert uns nur der Zustand ; seine Dynamik wird über die Verfolgung des Zustands von erhalten w.r.t. die Freiheitsgrade von :
Im Allgemeinen ist diese Gleichung, die Quanten-Master-Gleichung, mathematisch sehr kompliziert. In Anwendungen wird eine Vielzahl von Näherungen verwendet.
8.1. Quanten-Markov-Modell: Gorini-Kossakowski-Sudarshan-Lindbladequation
Die einfachste Annäherung der Quanten-Master-Gleichung (23) ist die Quanten-Markov-Dynamik, die durch die Gorini-Kossakowski-Sudarshan-Lindblad (GKSL)-Gleichung (Ingarden et al., 1997) gegeben ist (in der Physik wird sie allgemein einfach als Lindblad-Gleichung bezeichnet; Dies ist die einfachste Quanten-Master-Gleichung):
wobei Hermitescher Operator (Hamiltonian) beschreibt die innere Dynamik von und der Superoperator , im Raum der Dichteoperatoren agierend, beschreibt eine Interaktion mit der Umgebung .Dieser Superoperator wird oft Lindbladian genannt. Die GKSL-Gleichung ist eine Quantenmastergleichung für die Markovsche Dynamik. In diesem Beitrag haben wir keine Möglichkeit, den Begriff der Quanten-Markovianität näher zu erläutern. Die Quantenmastergleichung (23) beschreibt im Allgemeinen nicht-Markovsche Dynamik.
8.2. Biologische Funktionen im Quanten-Markov-Rahmen
Wir wenden uns mit der GKSL-Gleichung der offenen Systemdynamik zu. In unserer Modellierung Hamiltonian und Lindbladian stellen eine besondere biologische Funktion dar (siehe Khrennikov et al., 2018) für Details. Seine Funktionsweise ergibt sich aus dem Zusammenspiel von internen und externen Informationsflüssen. In den Abschnitten 10, 11.3, ist eine psychologische Funktion; im einfachsten Fall steht für eine gestellte Frage (sagen wir ist ein Mensch). In Abschnitt 7, ist die Genregulation des Glucose/Lactose-Stoffwechsels im Escherichia coli-Bakterium. In den Abschnitten 9, 11.2, stellt den Prozess der epigenetischen Mutation dar. Symbolisch biologische Funktion wird als Quantenobservable dargestellt: Hermitianischer Operator mit der Spektralzerlegung , wo Label-Ausgänge von . Die Theorie der Quanten-Markov-Zustandsdynamik beschreibt den Prozess der Erzeugung dieser Ausgaben.
Im mathematischen Modell (Asano et al., 2015b, Asano et al., 2017b, Asano et al., 2017a, Asano et al., 2015a, Asano et al., 2012b, Asano et al., 2011, Asano et al ., 2012a), die Ausgänge der biologischen Funktion
so dass es der spektralen Zerlegung von entspricht ,d.h.
wo
Das bedeutet, dass ist diagonal in einer orthonormalen Basis, die aus Eigenvektoren von besteht . Dieser Zustand, oder genauer gesagt, diese Zerlegung des Dichteoperators , ist die klassische statistische Mischung der grundlegenden Informationszustände, die diese biologische Funktion bestimmen. Die Wahrscheinlichkeiten in der Zustandszerlegung (26) werden statistisch interpretiert.
Stellen Sie sich ein großes Ensemble von Biosystemen mit dem Zustand vor Interaktion mit der Umwelt . (Wir erinnern uns, dass die Interaktion mathematisch im Lindbladian kodiert ist ) Aus dieser Interaktion ergibt sich eine biologische Funktion produziert Ausgabe mit Wahrscheinlichkeit .Wir bemerken, dass in den Operatortermen die Wahrscheinlichkeit ausgedrückt wird als
Diese Interpretation kann sogar auf ein einzelnes Biosystem angewendet werden, das viele Male auf dieselbe Umgebung trifft.
Zu beachten ist dieser Grenzzustand drückt die Stabilität gegenüber dem Einfluss der Betonumgebung aus . Natürlich würde in der realen Welt der Grenzzustand niemals erreicht werden. Die mathematische Formel (25) beschreibt den Prozess der Stabilisierung, Dämpfung von Schwankungen. Aber sie würden mit der Zeit nie ganz verschwinden.
Wir stellen fest, dass ein stationärer Zustand die stationäre GKSL-Gleichung erfüllt:
Es ist auch wichtig darauf hinzuweisen, dass im Allgemeinen ein stationärer Zustand der Quanten-Master-Gleichung nicht eindeutig ist, er hängt von der Klasse der Anfangsbedingungen ab.
8.3. Funktionsweise biologischer Funktionen durch Dekohärenz
Um die bisherigen Überlegungen zu konkretisieren, betrachten wir als Ausgangszustand einen reinen Quantenzustand. Angenommen, eine biologische Funktion ist dichotom, ,und es wird symbolisch durch den hermitischen Operator dargestellt, der auf orthonormaler Basis diagonal ist , .(Wir betrachten den zweidimensionalen Zustandsraum – den Qubit-Raum.) Der Anfangszustand habe die Form einer Überlagerung
wo . Die Quanten-Master-Dynamik ist keine reine Zustandsdynamik: Früher oder später (tatsächlich sehr bald) wird diese Überlagerung, die einen reinen Zustand darstellt, in eine Dichtematrix übertragen, die einen gemischten Zustand darstellt. Daher ist es von Anfang an sinnvoll, die Überlagerung (28) in Form einer Dichtematrix darzustellen:
Die Reinheit des Zustands, Überlagerung, ist durch das Vorhandensein von nicht-diagonalen Termen gekennzeichnet.
Superposition kodiert in unserem Fall Unsicherheit bezüglich der konkreten Zustandsbasis ,.Zunächst biologische Funktion war im Zustand der Ungewissheit zwischen zwei Möglichkeiten . Dies ist eine echte quanten(ähnliche) Unsicherheit. Unsicherheit über mögliche Aktionen in der Zukunft. Zum Beispiel für die psychologische Funktion (Abschnitt 10) die Antwort auf eine Frage darstellen, sagen Sie „Immobilien kaufen“ ( )und seine Negation ( ) , eine Person, deren Zustand durch Überlagerung (28) beschrieben wird, ist unsicher, mit ihr zu handeln( ) oder mit ( ) .Somit beschreibt ein überlagerungsartiger Zustand individuelle Ungewissheit, d. h. Ungewissheit, die mit dem individuellen Biosystem und nicht mit einem Ensemble von Biosystemen verbunden ist; mit dem einzigen Akt des Funktionierens von und nicht mit einer großen Serie solcher Taten.
Auflösung der Unsicherheit bzgl ist dadurch gekennzeichnet, dass die nicht-diagonalen Terme in (29) ausgewaschen werden. Die Quantendynamik (24) unterdrückt die nicht-diagonalen Terme und schließlich wird eine diagonale Dichtematrix erzeugt, die einen stationären Zustand dieses dynamischen Systems darstellt:
Dies ist eine klassische statistische Mischung. Es beschreibt ein Ensemble von Biosystemen; statistisch generieren sie Outputs mit Wahrscheinlichkeiten .Auf die gleiche Weise kann die statistische Interpretation für ein einzelnes System verwendet werden, das eine Leistung erbringt -Funktionieren zu verschiedenen Zeitpunkten (für eine lange Zeitreihe).
In der Quantenphysik ist der Prozess des Auswaschens der nichtdiagonalen Elemente in einer Dichtematrix als Dekohärenzprozess bekannt. Somit kann das beschriebene Modell als Operation der biologischen Funktion durch Dekohärenz bezeichnet werden.
8.4. Linearität der Quantendarstellung: exponentielle Beschleunigung der biologischen Funktion
Die quantenähnliche Modellierung behauptet nicht, dass Biosysteme grundsätzlich quantenhaft sind. Ein natürlicheres Bild ist, dass sie komplexe klassische biophysikalische Systeme sind und das quantenähnliche Modell die Informationsdarstellung klassischer biophysikalischer Prozesse in Genen, Proteinen, Zellen, Gehirnen liefert. Einer der Vorteile dieser Darstellung ist ihre Linearität. Der Quantenzustandsraum ist ein komplexer Hilbertraum und dynamische Gleichungen sind lineare Differentialgleichungen. Für endlichdimensionale Zustandsräume sind dies nur gewöhnliche Differentialgleichungen mit komplexen Koeffizienten (der Leser sollte sich also nicht vor so pathetischen Namen wie Schrödinger-, von Neumann- oder Gorini-Kossakowski-Sudarshan-Lindblad-Gleichungen scheuen). Die klassische biophysikalische Dynamik jenseits der Quanteninformationsdarstellung ist typischerweise nichtlinear und sehr kompliziert. Die Verwendung der linearen Raumdarstellung vereinfacht die Verarbeitungsstruktur. Es gibt zwei Sichtweisen auf diese Vereinfachung, externe und interne. Die erste ist die Vereinfachung der mathematischen Modellierung, d. h. die Vereinfachung der Untersuchung von Bioprozessen (durch uns, externe Beobachter). Der zweite ist zarter und interessanter. Auf eine wichtige Spezialität von Anwendungen der Quantentheorie in der Biologie haben wir bereits hingewiesen. Hier können Systeme Selbstbeobachtungen durchführen. Also, im Prozess der Evolution, sagen wir, eine Zelle kann durch solche Selbstbeobachtungen „lernen“, dass es rechnerisch rentabel ist, die lineare quantenähnliche Darstellung zu verwenden. Und jetzt kommen wir zum Hauptvorteil der Linearität.
Die lineare Dynamik beschleunigt die Informationsverarbeitung exponentiell. Lösungen der GKSL-Gleichung können im Formular dargestellt werden , wo ist der durch die rechte Seite der GKSL-Gleichung gegebene Superoperator. Im endlichdimensionalen Fall wird die Dekohärenzdynamik über Faktoren der Form ausgedrückt , wo . Solche Faktoren nehmen exponentiell ab. Die quantenähnliche lineare Realisierung biologischer Funktionen ist im Vergleich zur nichtlinearen klassischen Dynamik exponentiell schnell.
Die Verwendung der Quanteninformationsdarstellung bedeutet, dass im Allgemeinen große Cluster klassischer biophysikalischer Zustände durch wenige Quantenzustände codiert werden. Es bedeutet, dass riesige Informationen komprimiert werden. Es impliziert auch eine Erhöhung der Stabilität in der Zustandsverarbeitung. Verrauschte nichtlineare klassische Dynamik wird auf Dynamik abgebildet, die durch lineare quanten(ähnliche) Gleichungen vom Typ GKSL angetrieben wird.
Letzteres hat eine wesentlich einfachere Struktur und codiert über die Auswahl der Operatorkoeffizienten symbolisch die Interaktion innerhalb des Systems und mit seiner Umgebung , kann eine Dynamik mit Stabilisierungsregimen aufbauen, die zu stationären Zuständen führen.
9.Epigenetische Evolution in der Theorie offener Quantensysteme
In der Arbeit (Asano et al., 2012b) wurde im Rahmen der Theorie offener Quantensysteme ein allgemeines Modell der epigenetischen Evolution geschaffen, das neo-darwinistische mit neo-lamarckianischen Ansätzen vereint. Der Evolutionsprozess wird in Form einer adaptiven Dynamik dargestellt, die durch die quanten(ähnliche) Hauptgleichung gegeben ist, die die Dynamik des Informationszustands des Epigenoms im Prozess der Interaktion mit der Umgebung beschreibt. Dieses Modell der epigenetischen Evolution drückt die Wahrscheinlichkeiten für Beobachtungen aus, die an Epigenomen von Zellen gemacht werden können; dieses (quantenähnliche) Modell liefert keine detaillierte Beschreibung zellulärer Prozesse. Der quantenoperative Ansatz bietet eine Möglichkeit, alle bekannten Arten der zellulären epigenetischen Vererbung durch ein Modell zu beschreiben.
Um einen Hinweis auf das Modell zu geben, betrachten wir beispielsweise ein Gen . Das ist das System in Abschnitt 8.1. Es interagiert mit der Umgebung eine Zelle, die dieses Gen enthält, und andere Zellen, die Signale an diese konkrete Zelle und durch sie an das Gen senden . Als Folge dieser Interaktion gibt es eine epigenetische Mutation im Gen kann passieren. Es würde das Niveau der ändern -Bezeichnung
Im Moment ignorieren wir, dass es andere Gene gibt. In diesem stark vereinfachten Modell kann die Mutation innerhalb des zweidimensionalen Zustandsraums, des komplexen Hilbert-Raums, beschrieben werden (Qubit-Raum). Staaten von ohne und mit Mutation werden durch die orthogonale Basis dargestellt ,;diese Vektoren exprimieren mögliche epigenetische Veränderungen des fixierten Typs .
Ein reiner Quanteninformationszustand hat die Form einer Überlagerung.
Nun wenden wir uns dem allgemeinen Schema von Abschnitt 8.2 mit der biologischen Funktion zu ausdrücken -Epimutation in einem festen Gen. Die Quanten-Markov-Dynamik (24) löst die in Superposition codierte Unsicherheit auf („Modellierung von Epimutationen als Dekohärenz“). Die klassische statistische Mischung, siehe (30), angefahren wird. Seine diagonalen Elemente Geben Sie die Wahrscheinlichkeiten der Ereignisse an: „nein -Epimutation“ und “-Epimutation“. Diese Wahrscheinlichkeiten werden statistisch interpretiert: In einer großen Zellpopulation cells, , die Anzahl der Zellen mit -Epimutation ist .Das -Epimutation in einer Zellpopulation würde sich erst in unendlicher Zeit vollständig auf den stationären Zustand stabilisieren. Daher gibt es in Wirklichkeit Schwankungen (mit abnehmender Amplitude) in jedem endlichen Zeitintervall.
Schließlich weisen wir auf den Vorteil der quantenähnlichen Dynamik der Interaktion von Genen mit der Umwelt hin – die Linearität der Dynamik impliziert eine exponentielle Beschleunigung des Prozesses der epigenetischen Evolution (Abschnitt 8.4)..
10. Verbindung elektrochemischer Prozesse in neuronalen Netzen mit Quanteninformationsverarbeitung
Wie in der Einleitung betont wurde, sind quantenähnliche Modelle formale Operationsmodelle, die die Informationsverarbeitung in Biosystemen beschreiben. (im Gegensatz zum Studium der Quantenbiologie – der Wissenschaft über die echten quantenphysikalischen Prozesse in Biosystemen). Dennoch ist es interessant, die Struktur der Quanteninformationsverarbeitung in einem Biosystem mit darin enthaltenen physikalischen und chemischen Prozessen zu verbinden. Dies ist ein Problem von hoher Komplexität. Paper (Khrennikov et al., 2018) stellt einen Versuch vor, in diese Richtung für das menschliche Gehirn vorzugehen – das komplizierteste Biosystem (und gleichzeitig das interessanteste für Wissenschaftler). Im Rahmen der Quanteninformationstheorie wurde die Informationsverarbeitung durch die neuronalen Netze des Gehirns modelliert. Die Quanteninformationsformalisierung der Zustände neuronaler Netze ist mit den elektrochemischen Prozessen im Gehirn gekoppelt. Der Schlüsselpunkt ist die Darstellung der Unsicherheit, die durch das Aktionspotential eines Neurons erzeugt wird, als quanten(ähnliche) Überlagerung der grundlegenden mentalen Zustände, die einem neuralen Code entsprechen, siehe Abb. 1 zur Veranschaulichung.
Betrachten Sie die Informationsverarbeitung durch ein einzelnes Neuron; das ist das System (siehe Abschnitt 8.2). Sein Quanteninformationszustand entspricht dem Ruhe- und Zündzustand des neuralen Codes, , kann im zweidimensionalen Komplex dargestellt werden Hilbert-Raum (Qubit-Raum). Zu einem konkreten Zeitpunkt kann der Zustand eines Neurons mathematisch durch Überlagerung zweier Zustände beschrieben werden, die mit bezeichnet werden ,: .Es wird angenommen, dass diese Zustände orthogonal und normalisiert sind, d.h. and, . Die Koordinaten und in Bezug auf die ruhend feuernde Basis sind komplexe Amplituden, die Möglichkeiten für das Neuron darstellen ruhen oder feuern. Superposition repräsentiert Unsicherheit im Aktionspotential, „zu feuern“ oder „nicht zu feuern“. Diese Überlagerung ist eine Quanteninformationsdarstellung physikalischer, elektrochemischer Unsicherheit.
Lassen eine psychologische (kognitive) Funktion sein, die von diesem Neuron realisiert wird. (Natürlich ist dies eine zu starke Vereinfachung, betrachtet z. B. im Paradigma „Großmutter-Neuron“; siehe Abschnitt 11.3 zur Modellierung von basierend auf einem neuronalen Netz). Wir nehmen an, dass ist dichotom. Sagen steht für einen Instinkt, z. B. Aggression: „Angriff“ , „nicht angreifen“.
Eine psychologische Funktion kann die Beantwortung einer Frage (oder einer Klasse von Fragen), das Lösen von Problemen, das Ausführen von Aufgaben darstellen. Mathematisch wird durch den hermiteschen Operator dargestellt das ist diagonal in der Basis ,.Das Neuron interagiert mit der umgebenden elektrochemischen Umgebung .Diese Interaktion erzeugt die Entwicklung des Neuronenzustands und die Verwirklichung der psychologischen Funktion. Wir modellieren die Dynamik mit der Quantenmastergleichung (24). Dekohärenz transformiert den reinen Zustand in die klassische statistische Mischung (30), ein stationärer Zustand dieser Dynamik. Dies ist die Auflösung der ursprünglichen elektrochemischen Unsicherheit im Aktionspotential des Neurons.
Die diagonalen Elemente von Geben Sie die Wahrscheinlichkeiten mit der statistischen Interpretation an: in einem großen Ensemble von Neuronen (einzeln), die mit derselben Umgebung interagieren ,sagen Neuronen , ,die Anzahl der Neuronen, die die Entscheidung treffen gleich dem Diagonalelement .
Wir weisen auch auf den Vorteil der quantenähnlichen Dynamik der Interaktion eines Neurons mit seiner Umgebung hin – die Linearität der Dynamik impliziert eine exponentielle Beschleunigung des Prozesses der Zustandsentwicklung des Neurons hin zu einer „Entscheidungsmatrix“, die durch einen stationären Zustand gegeben ist (Abschnitt 8.4).
11.Zusammengesetzte Biosysteme
11.1. Verschränkung von Informationszuständen von Biosystemen
Der Zustandsraum des Biosystems bestehend aus den Subsystemen , ist das Tensorprodukt der Zustandsräume von Subsystemen ,So
| * |
Der einfachste Weg, sich diesen Zustandsraum vorzustellen, besteht darin, seine Koordinatendarstellung in Bezug auf eine Basis zu betrachten, die mit Basen konstruiert wurde .Betrachten Sie der Einfachheit halber den Fall von Qubit-Zustandsräumen lassen , , sei eine orthonormale Basis in ,d.h. Elemente dieses Raumes sind Linearkombinationen der Form . (Um ganz formal zu sein, müssen wir Basisvektoren mit dem Index kennzeichnen , d.h.,. Aber wir werden das weglassen.) Dann Vektoren bilden die orthonormale Basis in ,d.h. irgendein Zustand können im Formular dargestellt werden
und die komplexen Koordinaten sind normalisiert: . Zum Beispiel, wenn , wir können den Staat betrachten
Dies ist ein Beispiel für einen verschränkten Zustand, d. h. einen Zustand, der nicht in das Tensorprodukt der Zustände der Subsysteme zerlegt werden kann. Ein Beispiel für einen unverschränkten Zustand (bis zur Normalisierung) ist gegeben durch
Verschränkte Zustände sind grundlegende Zustände für Quantencomputer, die die Untrennbarkeit von Zuständen untersuchen. Das Einwirken auf ein konkretes Qubit ändert den gesamten Zustand. Bei einem trennbaren Zustand ändern wir beispielsweise durch Transformieren des ersten Qubits nur den Zustand des Systems .Diese Möglichkeit, den sehr komplexen Zustand eines zusammengesetzten Systems durch Änderung des lokalen Zustands eines Teilsystems zu ändern, wird als Wurzel der Überlegenheit der Quantencomputer gegenüber der klassischen angesehen. Wir bemerken, dass die Dimension des Tensorprodukt-Zustandsraums sehr groß ist, sie ist gleich für Qubit-Subsysteme. In der Quantenphysik wird diese Möglichkeit, mit dem zusammengesetzten Zustand (der die große Dimension haben kann) zu manipulieren, typischerweise mit „Quanten-Nichtlokalität“ und gespenstischer Fernwirkung in Verbindung gebracht. Aber auch in der Quantenphysik ist diese nichtlokale Interpretation die Quelle ständiger Debatten []. Insbesondere in der jüngsten Schriftenreihe [] wurde gezeigt, dass es möglich ist, ohne Bezugnahme auf die Quanten-Nichtlokalität vorzugehen, und dass die Quantenmechanik als die lokale physikalische Theorie interpretiert werden kann. Die lokale Sichtweise auf die Quantentheorie ist für biologische Anwendungen natürlicher.13 Für Biosysteme ist spukhafte Fernwirkung wirklich mysteriös; für den Menschen entspricht es der Akzeptanz parapsychologischer Phänomene.
Wie kann man die Erzeugung der Zustandstransformation des zusammengesetzten Systems erklären? B. durch „lokale Transformation“ des Zustands seines Subsystems ? Die Schlüsselrolle spielen dabei Korrelationen, die in verschränkten Zuständen symbolisch kodiert sind. Betrachten Sie zum Beispiel das zusammengesetzte System im Staat gegeben durch (33). Betrachten Sie die Observablen vom Projektionstyp An dargestellt durch hermitesche Operatoren mit Eigenvektoren ,(in Qubit-Räumen ). Messung von sagen mit der Ausgabe induziert die Zustandsprojektion auf den Vektor .
Daher Messung von erzeugt automatisch die Ausgabe . Also der Staat codiert die genauen Korrelationen für diese beiden Observablen. Ebenso der Staat
kodiert Zusammenhänge , (Mod 2).
„Ein verschränkter Zustand liefert also die symbolische Darstellung von Korrelationen zwischen Zuständen der Subsysteme eines zusammengesetzten Biosystems“.
Die Theorie offener Quantensysteme arbeitet mit gemischten Zuständen, die durch Dichteoperatoren beschrieben werden. Und bevor wir uns der Modellierung biologischer Funktionen für zusammengesetzte Systeme zuwenden, definieren wir Verschränkung für gemischte Zustände. Betrachten Sie den Fall des Tensorprodukts zweier Hilbert-Räume, dh des Systems ist eine Verbindung aus zwei Teilsystemen und . Ein gemischter Zustand von gegeben von heißt separabel, wenn es sich als konvexe Kombination von Produktzuständen darstellen lässt , wo , ,sind der Dichteoperator des Subsystems of .Nicht trennbare Zustände heißen verschränkt. Sie repräsentieren symbolisch Zusammenhänge zwischen Subsystemen.
Die Quantendynamik beschreibt die Evolution dieser Korrelationen. Im Rahmen der Dynamik offener Systeme nähert sich eine biologische Funktion über den Prozess der Dekohärenz dem stationären Zustand. Wie in Abschnitt 8.3 diskutiert wurde, löst diese Dynamik Ungewissheiten auf, die ursprünglich im Zustand eines Biosystems vorhanden waren; Gleichzeitig wäscht es auch die Korrelationen aus: den stationären Zustand, der in der Basis diagonal ist ist trennbar (entwirrt). Im Prozess der Zustandsentwicklung spielen jedoch Korrelationen zwischen Subsystemen (Verschränkung) die entscheidende Rolle. Ihre Anwesenheit führt zu Zustandsänderungen des zusammengesetzten Systems über „lokale Transformationen“ der Zustände seiner Subsysteme. Eine solche korrelierte Dynamik des globalen Informationszustands spiegelt die Konsistenz der Transformationen der Zustände von Subsystemen wider.
Da der quantenähnliche Ansatz auf der Quanteninformationsdarstellung von Systemzuständen basiert, können wir die physische Raumposition von Biosystemen vergessen und im Informationsraum arbeiten, der durch den komplexen Hilbert-Raum gegeben ist . In diesem Raum können wir den Begriff der Lokalität basierend auf der Fixed-Tensor-Product-Zerlegung (31) einführen. Operationen in ihren Komponenten wir können lokal anrufen (im Informationsraum). Aber sie induzieren eine „informationell nicht-lokale“ Evolution des Zustands des zusammengesetzten Systems.
11.2. Verschränkung von Epimutationen von Genen
Nun kommen wir auf das in Abschnitt 9 vorgestellte Modell zurück und betrachten den Informationszustand des Epigenoms der Zelle, das potenzielle Epimutationen des Chromatin-Markierungstyps exprimiert. Lassen Sie das Genom der Zelle bestehen aus Gene . Für jedes Gen , Betrachten Sie alle möglichen Epimutationen und zählen Sie sie auf: .Der Zustand aller potenziellen Epimutationen im Gen wird als Überlagerung dargestellt
Im Idealfall – Epimutationen der Gene sind unabhängig – wird der Zustand des Epigenoms der Zelle mathematisch durch das Tensorprodukt der Zustände beschrieben :
In einem lebenden Biosystem sind jedoch die meisten Gene und Proteine korreliert und bilden ein großes Netzwerksystem. Daher wirkt sich eine Epimutation auf andere Gene aus. Im Rahmen der Quanteninformation wird diese Situation durch verschränkte Zustände beschrieben:
Diese Form der Darstellung potenzieller Epimutationen im Genom einer Zelle impliziert, dass Epimutationen in einem Gen mit Epimutationen in anderen Genen übereinstimmen. Wenn der Zustand verstrickt (nicht faktorisiert) ist, dann durch Einwirkung, d.h. durch Veränderung der Umwelt, sagen wir auf ein Gen , und indem sie eine Epimutation darin induziert, kann die Zelle konsistente Epimutationen in anderen Genen „induzieren“.
Die Linearität der Quanteninformationsdarstellung der biophysikalischen Prozesse in einer Zelle induziert die lineare Zustandsdynamik. Dies macht die epigenetische Evolution sehr schnell; die nicht-diagonalen Elemente der Dichtematrix nehmen exponentiell schnell ab. Somit rechtfertigt unser quantenähnliches Modell die hohe Geschwindigkeit der epigenetischen Evolution. Wenn es allein auf der biophysikalischen Darstellung mit nichtlinearer Zustandsdynamik basieren würde, wäre es wesentlich langsamer.
Die Modellierung auf der Grundlage der Theorie offener Systeme führt zu einer Neubetrachtung der Wechselbeziehung zwischen dem Darwinschen und dem Lamarckschen Standpunkt zur Evolution. Hier haben wir uns auf Epimutationen konzentriert, aber genauso können wir Mutationen modellieren (Asano et al., 2015b).
11.3.Psychische Funktionen
Nun wenden wir uns dem in Abschnitt 10 vorgestellten Modell zu. Ein neuronales Netzwerk wird als zusammengesetztes Quantensystem modelliert; sein Zustand wird als Tensorprodukt von Einzelneuronen-Zustandsräumen dargestellt. Die Funktionen des Gehirns führen Selbstmessungen durch, die in der Theorie offener Quantensysteme modelliert sind. (Es besteht keine Notwendigkeit, den Zusammenbruch des Staates zu berücksichtigen.) Die Dynamik des Staates einer Gehirnfunktion (psychologische Funktion) wird durch die Quanten-Master-Gleichung beschrieben. Seine stationären Zustände stellen klassische statistische Mischungen möglicher Ausgänge dar (Entscheidungen). Also durch Wechselwirkung mit der elektrochemischen Umgebung, (als offenes System angesehen) löst Unsicherheiten auf, die ursprünglich im verschränkten Zustand kodiert waren und Unsicherheiten in Aktionspotentialen von Neuronen und Korrelationen zwischen ihnen darstellen.
Die Verschränkung spielt die entscheidende Rolle bei der Erzeugung von Konsistenz in der Dynamik von Neuronen. Nehmen Sie wie in Abschnitt 11.1 an, dass die Quanteninformationsdarstellung auf basiert 0–1 Code. Betrachten Sie ein Netzwerk von Neuronen interagieren mit der umgebenden elektrochemischen Umgebung , einschließlich Signalisierung von anderen neuronalen Netzen. Der Informationszustand ist durch (32) gegeben. Verschränkung codiert Korrelationen zwischen dem Feuern einzelner Neuronen. Beispielsweise ist der Zustand (33) zwei synchron feuernden Neuronen und der Zustand (34) zwei asynchron feuernden Neuronen zugeordnet.
Ausgänge der psychologischen Funktion biophysikalisch auf einem neuronalen Netzwerk beruhen, resultieren aus konsistenten Zustandsdynamiken einzelner Neuronen, die zu diesem Netzwerk gehören. Wie bereits betont wurde, ist die Entwicklung des Zustands in Richtung eines stationären Zustands sehr schnell, als Folge der Linearität der Dynamik des offenen Systems; die nicht-diagonalen Elemente der Dichtematrix nehmen exponentiell schnell ab.
12. Abschließende Bemerkungen
Seit 1990 (Khrennikov, 1999) blühte die quantenähnliche Modellierung außerhalb der Physik, insbesondere die Modellierung von Kognition und Entscheidungsfindung, weltweit auf. Die Quanteninformationstheorie (gekoppelt mit Theorien zu Messungen und offenen Quantensystemen) ist ein fruchtbarer Boden für quantenähnliche Blumen. Die in diesem Beitrag vorgestellte Grundhypothese ist, dass das Funktionieren von Biosystemen auf der Quanteninformationsrepräsentation ihrer Zustände basiert. Diese Darstellung ist das Ergebnis der biologischen Evolution. Letzteres wird als Evolution im Informationsraum betrachtet. Biosysteme reagieren also nicht nur auf Material- oder Energiezwänge der Umwelt, sondern auch auf Informationszwänge. In diesem Beitrag werden biologische Funktionen als offene Informationssysteme betrachtet, die mit der Informationsumgebung interagieren.
Die quantenähnliche Darstellung von Informationen bietet die Möglichkeit, Überlagerungen zu verarbeiten. Diese Art der Informationsverarbeitung ist vorteilhaft, da Rechenressourcen eingespart werden: eine biologische Funktion müssen keine in Überlagerungen codierten Unsicherheiten auflösen und JPDs aller kompatiblen Variablen berechnen, die an der Leistung von beteiligt sind .
Ein weiteres vorteilhaftes Merkmal der quantenähnlichen Informationsverarbeitung ist ihre Linearität. Der Übergang von der nichtlinearen Dynamik elektrochemischer Zustände zu einer linearen quantenähnlichen Dynamik beschleunigt die Zustandsverarbeitung enorm (für Genexpression, Epimutationen und allgemeine Entscheidungsfindung). Entscheidungsträger sind in diesem Rahmen Gene, Proteine, Zellen, Gehirne, Ökosysteme.
BIologische Funktionen haben die Fähigkeit entwickelt, Selbstmessungen durchzuführen und Ergebnisse ihrer Funktionsweise zu erzeugen. Wir modellieren diese Fähigkeit im Rahmen offener Quantensysteme als Entscheidungsfindung durch Dekohärenz. Wir betonen, dass dieses Modell frei von der mehrdeutigen Vorstellung des Zusammenbruchs der Wellenfunktion ist.
Korrelationen innerhalb einer biologischen Funktion sowie zwischen verschiedenen biologischen Funktionen und der Umgebung werden linear durch verschränkte Quantenzustände dargestellt.
Wir hoffen, dass dieses Papier für Biologen (insbesondere, die an mathematischer Modellierung arbeiten) als Einführung in den quantenähnlichen Ansatz zur Modellierung der Funktionsweise von Biosystemen nützlich ist. Wir hoffen auch, dass es die Aufmerksamkeit von Experten der Quanteninformationstheorie auf die Möglichkeit lenken kann, seinen Formalismus und seine Methodik in biologischen Studien einzusetzen.
Erklärung konkurrierender Interessen
Die Autoren erklären, dass ihnen keine konkurrierenden finanziellen Interessen oder persönlichen Beziehungen bekannt sind, die die in diesem Dokument beschriebene Arbeit beeinflusst haben könnten.
Danksagungen
Diese Arbeit wurde teilweise von JSPS, Japan KAKENHI, Nr. 26247016 und 17K19970 unterstützt. MO dankt der IRI-NU-Kollaboration, Japan, für die Unterstützung.
- ↑ Newton Isaac, «Philosophiae naturalis principia mathematica», Benjamin Motte, 1687, London UK».
- ↑ Kolmogorov A.N.Grundbegriffe Der Wahrscheinlichkeitsrechnung. Springer-Verlag, Berlin (1933)
- ↑ Penrose R. The Emperor’S New Mind Oxford Univ. Press, New-York (1989)
- ↑ Umezawa H. Advanced Field Theory: Micro, Macro and Thermal Concepts AIP, New York (1993)
- ↑ Hameroff S. Quantum coherence in microtubules. a neural basis for emergent con- sciousness? J. Cons. Stud., 1 (1994)
- ↑ Vitiello G. Dissipation and memory capacity in the quantum brain model Internat. J. Modern Phys. B, 9 (1995), p. 973
- ↑ Vitiello G. My Double Unveiled: The Dissipative Quantum Model of Brain, Advances in Consciousness Research, John Benjamins Publishing Company(2001)
- ↑ Arndt M., Juffmann T., Vedral V. Quantum physics meets biology HFSP J., 3 (6) (2009), pp. 386-400, 10.2976/1.3244985
- ↑ Bernroider G., Summhammer J. Can quantum entanglement between ion transition states effect action potential initiation? Cogn. Comput., 4 (2012), pp. 29-37
- ↑ Bernroider G. Neuroecology: Modeling neural systems and environments, from the quantum to the classical level and the question of consciousness J. Adv. Neurosci. Res., 4 (2017), pp. 1-9
- ↑ Plotnitsky A. Epistemology and Probability: Bohr, Heisenberg, SchrÖdinger and the Nature of Quantum-Theoretical Thinking Springer, Berlin, Germany; New York, NY, USA (2009
- ↑ 12.0 12.1 12.2 12.3 12.4 Khrennikov A., Basieva I., PothosE.M., Yamato I. Quantum Probability in Decision Making from Quantum Information Representation of Neuronal States, Sci. Rep., 8 (2018), Article 16225 Cite error: Invalid
<ref>tag; name ":0" defined multiple times with different content - ↑ Khrennikov A. On quantum-like probabilistic structure of mental information Open Syst. Inf. Dyn., 11 (3) (2004), pp. 267-275
- ↑ 14.0 14.1 Asano M., Basieva I., Khrennikov A., Ohya M., Tanaka Y., Yamato I. Quantum information biology: from information interpretation of quantum mechanics to applications in molecular biology and cognitive psychology Found. Phys., 45 (10) (2015), pp. 1362-1378
- ↑ 15.0 15.1 Kolmogorov A.N. Grundbegriffe Der Wahrscheinlichkeitsrechnung Springer-Verlag, Berlin (1933)
- ↑ 16.0 16.1 Davies E.B., Lewis J.T. An operational approach to quantum probability Comm. Math. Phys., 17 (1970), pp. 239-260
- ↑ 17.0 17.1 Davies E.B. Quantum Theory of Open Systems. Academic Press, London (1976)
- ↑ 18.0 18.1 Ozawa M. Quantum measuring processes for continuous observables J. Math. Phys., 25 (1984), pp. 79-87
- ↑ 19.0 19.1 Yuen, H. P., 1987. Characterization and realization of general quantum measurements. M. Namiki and others (ed.) Proc. 2nd Int. Symp. Foundations of Quantum Mechanics, pp. 360–363.
- ↑ 20.0 20.1 Ozawa M. An operational approach to quantum state reduction Ann. Phys., NY, 259 (1997), pp. 121-137
- ↑ 21.0 21.1 Ozawa M. Uncertainty relations for noise and disturbance in generalized quantum measurements Ann. Phys., NY, 311 (2004), pp. 350-416
- ↑ 22.0 22.1 Okamura K., Ozawa M. Measurement theory in local quantum physics J. Math. Phys., 57 (2016), Article 015209
- ↑ Von Neumann J. Mathematical Foundations of Quantum Mechanics Princeton Univ. Press, Princeton, NJ, USA (1955)
- ↑ Khrennikov A. Information Dynamics in Cognitive, Psychological, Social, and Anomalous Phenomena, Ser.: Fundamental Theories of Physics, Kluwer, Dordreht(2004)
- ↑ 25.0 25.1 Busemeyer J., Bruza P. Quantum Models of Cognition and Decision Cambridge Univ. Press, Cambridge(2012)
- ↑ Bagarello F. Quantum Concepts in the Social, Ecological and Biological Sciences Cambridge University Press, Cambridge (2019)
- ↑ Bagarello F., Basieva I., Pothos E.M., Khrennikov A. Quantum like modeling of decision making: Quantifying uncertainty with the aid of heisenberg-robertson inequality J. Math. Psychol., 84 (2018), pp. 49-56
- ↑ Khrennikov A., Basieva I., DzhafarovE.N., Busemeyer J.R. Quantum models for psychological measurements: An unsolved problem. PLoS One, 9 (2014), Article e110909
- ↑ Basieva I., Khrennikov A. On the possibility to combine the order effect with sequential reproducibility for quantum measurements Found. Phys., 45 (10) (2015), pp. 1379-1393
- ↑ Ozawa M., Khrennikov A. Application of theory of quantum instruments to psychology: Combination of question order effect with response replicability effect Entropy, 22 (1) (2020), pp. 37.1-9436
- ↑ Ozawa M., Khrennikov A. Modeling combination of question order effect, response replicability effect, and QQ-equality with quantum instruments (2020)
- ↑ Ingarden R.S., Kossakowski A., Ohya M. Information Dynamics and Open Systems: Classical and Quantum Approach Kluwer, Dordrecht (1997)
- ↑ Schrödinger E. What Is Life? Cambridge university press, Cambridge (1944)
- ↑ Asano M., Basieva I., Khrennikov A., Ohya M., Tanaka Y., Yamato I. Towards modeling of epigenetic evolution with the aid of theory of open quantum systems AIP Conf. Proc., 1508 (2012), p. 75 https://aip.scitation.org/doi/abs/10.1063/1.4773118
- ↑ 35.0 35.1 35.2 Asano M., Khrennikov A., Ohya M., Tanaka Y., Yamato I. Quantum Adaptivity in Biology: From Genetics To Cognition Springer, Heidelberg-Berlin-New York(2015)
- ↑ Asano M., Ohya M., Tanaka Y., BasievaI., Khrennikov A. Quantum-like model of brain’s functioning: decision making from decoherence J. Theor. Biol., 281 (1) (2011), pp. 56-64
- ↑ Khrennikov A. Probability and Randomness: Quantum Versus Classical Imperial College Press (2016)
- ↑ Khrennikov A. Ubiquitous Quantum Structure: From Psychology To Finances Springer, Berlin-Heidelberg-New York(2010)
- ↑ Khrennikov A. Ubiquitous Quantum Structure: From Psychology To Finances Springer, Berlin-Heidelberg-New York(2010)
- ↑ Wang Z., Busemeyer J.R. A quantum question order model supported by empirical tests of an a priori and precise prediction. Top. Cogn. Sci., 5 (2013), pp. 689-710
- ↑ 41.0 41.1 Ozawa M., Khrennikov A. Application of theory of quantum instruments to psychology: Combination of question order effect with response replicability effect Entropy, 22 (1) (2020), pp. 37.1-9436
particularly focusing on the field of the neurophysiology of the masticatory system


![{\displaystyle [{\hat {A}},{\hat {B}}]\neq 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca6253a4b7d1fed6f0b83ee4f14d05f740af438)


























![{\displaystyle {\frac {d{\hat {\rho }}}{dt}}(t)=-i[{\hat {\mathcal {H}}},{\hat {\rho }}(t)],{\hat {\rho }}(0)={\hat {\rho }}_{0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/46cb03104a69d14e36fd6776550cc38a492b9634)





![{\textstyle Pr\{A=x||\rho \}=Tr[{\widehat {E}}^{A}(x)\rho ]=Tr[{\widehat {E}}^{A}(x)\rho {\widehat {E}}^{A}(x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dffc6a2b1bbc16202b1abab10b045f1fcc304c04)






















![{\textstyle Pr\{{\text{x}}=x||\rho \}=Tr[{\hat {D}}(x)\rho ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/229874a62a1d92651c5a1e60265399c0e969dd05)






![{\textstyle Pr\{{\text{x}}=x||\rho \}=Tr[{V}(x)\rho {V}^{*}(x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd51eeb8f4e5b9cd30d856040525bb2be6f94c0b)



![{\textstyle \rho \rightarrow \rho _{({\text{x}}=x)}={\frac {{\mathcal {L}}_{A}(x)\rho }{Tr[{\mathcal {L}}_{A}(x)\rho ]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c622ed9f3472b9bc13374d7bd37e7da807ab612)


![{\textstyle Pr\{{\text{x}}=x||\rho \}=Tr[\Im _{A}(x)\rho ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/586d4e469a1b620c551892a44aab492958653f02)


![{\textstyle Pr\{{\text{A}}=x||\rho \}=Tr[{\widehat {D}}^{A}(x)\rho ]=Tr[{\widehat {E}}^{A}(x)\rho ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9a8550566f3459e7cddbf180fcde8f50d4c299b)




![{\textstyle \rho \rightarrow \rho _{({\text{A}}=x)}={\frac {{V}(x)\rho V(x)^{*}}{Tr[{V}(x)\rho V(x)^{*}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba54c1d316d7ab6acff66de4f7dc854ac7eda6f0)




























![{\displaystyle Pr\{A=x\|\rho \}=Tr[{\Bigl (}I\otimes E^{M}{^{_{A}}(x){\Bigr )}}U(\rho \otimes \sigma )U^{*}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f3cd4375be3c41ac3dd1be33638372ab6f99ec1)



![{\displaystyle {\mathcal {P}}_{A}(x)\rho =Tr_{\mathcal {H}}[{\Bigl (}I\otimes E^{M}{^{_{A}}(x){\Bigr )}}U(\rho \otimes \sigma )U^{*}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/30510a056cd9495c058447715652efe281343aee)












![{\displaystyle [{\widehat {A}},{\widehat {B}}]\neq 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e9db6c1b5e87d54bf434dd1a9c5e27aec96f01b)



![{\displaystyle [{\mathcal {J_{A}(x)}},{\mathcal {J_{B}(x)}}]={\mathcal {J_{A}(x)}}{\mathcal {J_{B}(x)}}-{\mathcal {J_{B}(x)}},{\mathcal {J_{A}(x)}}\neq 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/361fd78b0a02b9327edd624db3524e24db18c76b)

![{\displaystyle \rho ,[\Im _{A}(x),\Im _{B}(x)]\rho =0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e92482fee8da2743e673c367d456a5072ea1ade)
![{\displaystyle [\Im _{A}(x),\Im _{B}(x)]\neq 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f79e1311a59bf9e0fb79419b798b7ed5b018f921)






















![{\displaystyle {\tfrac {d{\widehat {R}}}{dt}}(t)=-i[{\widehat {H}},{\widehat {R}},(t)],{\widehat {R}}(0)={\widehat {R}}_{0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5360ff03d80449ad8d6c2745e7b1ce43093e52c)



![{\displaystyle {\tfrac {d{\widehat {\rho }}}{dt}}(t)=-i[{\widehat {H}},{\widehat {\rho }},(t)]+{\widehat {L}}[{\widehat {\rho }}(t),{\widehat {\rho }}(0)={\widehat {\rho }}_{0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ced507a031874df17864ed03824140ff695bf48)















![{\displaystyle i[{\widehat {H}},{\widehat {\rho }}_{steady}]={\widehat {L}}[{\widehat {\rho }}_{steady}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f2a348496cb945fd0a1351418b60d74ad83430c)





























































































