Conclusion of the ‘Normal Science’ section

Conclusion of the ‘Normal Science’ section

Abstract

This chapter details the use of Bayes' Theorem in diagnosing Temporomandibular Disorders (TMD) using the RDC (Research Diagnostic Criteria) classification criteria. The analysis focuses on determining the sensitivity and specificity of the diagnostic test, calculating the overall probability that a patient with a positive test result is actually affected by TMD based on a disorder prevalence of 9% in the examined population. The Bayes model is used to update diagnostic probabilities based on new clinical evidence. Key elements of the model include: 'Prevalence' $P(A)$: The frequency with which the TMD condition occurs in the general population, estimated at 9%; 'Sensitivity' $P(B|A)$: The probability that the diagnostic test correctly identifies a patient affected by TMD as such; 'Specificity' $P(\neg B|\neg A)$: The probability that the test correctly excludes those not affected by TMD. The Bayes' Theorem formula is as follows: $P(A|B)={\frac {P(B|A)\cdot P(A)}{P(B)}}$ This formula is used to calculate the post-test probability that a patient is affected by TMD given a positive test result. We use data collected from 40 subjects undergoing the RDC test: 9 subjects were identified as affected by TMD and 1 subject was a false negative. The calculation method is based on total probability and conditional probability to determine the test's effectiveness in correctly diagnosing TMD. Concerns are raised about the possibility that other serious pathologies could mimic TMD symptoms, potentially confusing test results. Therefore, the need for a thorough and multidisciplinary follow-up to verify the reliability of test results and to exclude other medical conditions that might present similar symptoms is emphasized.

The discussion concludes by emphasizing the importance of adopting a diagnostic approach that integrates the best practices and methodologies available. It is suggested that the adoption of quantum models in addition to the traditional Bayes model could significantly improve the accuracy of medical diagnoses, providing clinicians with more robust tools to interpret diagnostic test results and manage diseases more effectively.

 

 

Introduction

We have reached the conclusion of the 'Normal Science' section, which fundamentally equates to phase 2 of 'Kuhn's Paradigms' where the status quo of the paradigm in the field of Orofacial Pain (OP) and Temporomandibular Disorders (TMDs) has been presented. At the same time, a range of diagnostic issues that are not yet classifiable as 'Anomalies' but rather as critical elements to evaluate within the chapter context were highlighted.

Chronic 'OP' conditions can be particularly challenging to diagnose and treat due to their complexity and limited understanding of the mechanisms underlying their etiology and pathogenesis. A frequent characteristic of 'OP' is the multifactorial nature of the pathology, which further complicates diagnosis. TMDs, for example, referred to variously as Temporo-Mandibular Disorders (TMDs), Cranio Facial Pain (CFP), and Temporo-Mandibular Joint Dysfunction (TMJ dysfunction) in Anglo-Saxon countries, sometimes present diagnostic challenges. The orofacial pain caused by TMDs often overlaps with symptoms and clinical signs similar to other painful disorders, which may be manifestations of other systemic neurological diseases. This clinical scenario can make differential diagnosis difficult, especially in the early stages of the disease. In a percentage of patients with functional disorders of the stomatognathic apparatus, some peripheral risk factors, i.e., occlusal, have been identified as well as a series of central biopsychosocial risk factors concerning Central Nervous System dysfunctions. However, these studies have not provided new information on the main causes of TMDs and their implications for managing these patients and consequently, a wide variety of mostly conservative treatments have been proposed but the lack of clinical evidence has allowed the role of occlusion in TMDs to be contested although there is no scientific evidence contradicting a causal occlusal role in functional disorders.

In conclusion, a critical obstacle in understanding TMDs and consequently in differential diagnosis with 'OP' has been the loss of standardized diagnostic criteria for defining subtypes of TMDs, and for this reason numerous studies have been conducted to create a standardized diagnostic evaluation method called Research Diagnostic Criteria (RDC) and signed in RDC. For more information on the RDC theme follow the specific chapter.

The fact is that in previous chapters we have highlighted critical issues not to be underestimated both for the delay in diagnosis and for the danger of diagnostic errors that can compromise the health of patients as well documented in the presentation of clinical cases. The prospective clinical study, which we will present in this chapter, will form the foundation of a new diagnostic paradigm that we will see realized at the end of the editorial writing of Masticationpedia and precisely in the 'Extraordinary Science' section. Given the complexity, delicacy, and criticality of the subject, the prospective clinical study lasted 5 years during which the subjects involved were studied, followed, and re-examined at three different times: at a time $t_{0}=$ Preliminary diagnostic phase; a time $t_{n}=$ Advanced diagnostic phase and finally a time $t_{n+1}=$ Definitive diagnostic phase that will close the project from which a protocol called 'Index $|\Psi \rangle$' will be modeled, read as 'Index ket Psi'.

The accuracy of the data derived from the prospective study at various evaluation times has been correlated with the Bayesian model, which is why it is necessary to briefly recall it.

Bayes' Theorem

Bayes' theorem is an important principle of probability theory that allows us to update beliefs or probabilities about an event in light of new evidence or information. In other words, it allows us to recalculate the probability of a hypothesis, given the observation of some data.

The formula for Bayes' Theorem is:

$P(A|B)={\frac {P(B|A)\cdot P(A)}{P(B)}}$

where:

• $P(A|B)$ - Probability that A occurs after observing B,
• $P(B|A)$ - Probability of observing B if A is true,
• $P(A)$ - Initial probability of A,
• $P(B)$ - Total probability.

$P(B)$ is crucial for understanding the discussion that follows. It is often called the 'Total Probability Formula'.

In simple terms, Bayes' theorem tells us how to update our belief about a hypothesis (event A) in light of new evidence (event B). Practically, it can be useful when we have preliminary knowledge about the probability of an event $P(A)$ and obtain new information that might influence this probability $P(B|A)$. Bayes' theorem allows us to calculate the updated probability of the event $A$ in light of this new information. A common example is the diagnostic test in medicine. Suppose we have a rare disease, with a 1% probability of affecting the population. The test for this disease has a sensitivity of 80% and a specificity of 90%. If we get a positive test result, how should we interpret it?

Using Bayes' theorem, we can calculate the probability that a person actually has the disease given the positivity of the test. This involves calculating the conditional probabilities of the disease given a positive test result, using information on the test's sensitivity and specificity along with the prevalence of the disease in the population.

In short, Bayes' theorem provides a powerful way to update our beliefs or probabilities based on new evidence or information, making it a fundamental tool in many areas, from statistics to medicine, to artificial intelligence.

At this point, we can transfer the results of the RDC test into Bayes and quantify the probabilities of clinical positivity and/or negativity. We begin with the data exiting the first analysis of the sample based on the classic RDC model and called Index $\Psi$ at time $t_{0}$

Index $\Psi$ at time $t_{0}$

We begin with an overview of the results obtained from the RDC model applied to a sample of 30 asymptomatic and 10 symptomatic subjects, analyzing the sensitivity and specificity of the test and, consequently, the total probability calculated through Bayes' theorem. This theorem is fundamental for evaluating the probability that a patient with a positive test is actually affected by the disease.

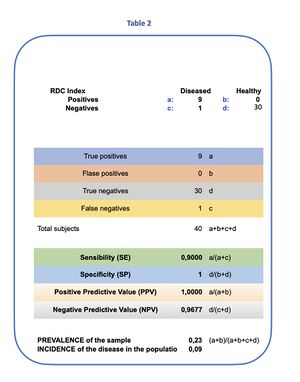
The model identified 9 symptomatic subjects affected by TMDs who met the RDC clinical criteria, and one healthy subject among the symptomatic, with a disease prevalence of Template:Red start9% Template:Red end in the examined population. (Table 1) We proceed to apply Bayes' theorem to the statistical data.

Based on the results of the RDC test for our 40 subjects, of which 9 were considered affected by TMDs and 1 as a false negative, we proceed as follows:

• Prevalence ($P(A)$): 9%,
• Sensitivity ($P(B|A)$): 90%,
• Specificity ($P(\neg B|\neg A)$): 100%, thus $P(B|\neg A)=0$.

Calculation of the Total Probability Formula $P(B)$

$P(B)=P(B|A)\cdot P(A)+P(B|\neg A)\cdot (1-P(A))=0.081$

This calculation is essential for addressing the concepts that will follow.

Calculation of $P(A|B)$

$P(A|B)={\frac {0.90\cdot 0.09}{0.081}}=1.00$

Thus, $P(A|B)$ represents the probability that the patient is ill with TMDs given that the test result is positive. This result, which indicates a 100% certainty in the diagnosis after a positive RDC test for TMDs, raises concerns about the high value of probabilistic certainty and the possible presence of other serious pathologies that could manifest symptoms similar to TMDs in an early stage.

Martina K. Shephard and Gary Heir illustrate in their scientific article that various pathological conditions can confuse the diagnosis of Orofacial Pain, such as TMDs, including cardiovascular diseases, musculoskeletal disorders, and neurological conditions.

For this reason, we subjected the symptomatic subjects to further evaluation by a multidisciplinary team. The follow-up, concluded after two years, provided significant answers to the expressed doubts, demonstrating the complexity of medical diagnoses and the importance of a holistic approach in symptom evaluation. Indeed, the updated data were recalculated concurrently with a series of alternative statistical settings. This second step was called, appropriately, 'Index $\Psi$' at time $t_{n}$

Table 2: Results regarding the accuracy of the RDC test

Index $\Psi$' at time $t_{n}$

The two-year follow-up revealed that many of the 10 symptomatic subjects were affected by serious neurological and systemic diseases, such as meningiomas, pineal cavernomas, scleroderma, and hemimasticatory spasms. These conditions have already been described in the chapters of the "Normal Science" section. The discovery of such serious pathologies among the subjects examined has raised considerable concern, revealing a high risk to life for some individuals. This result should be interpreted as an epistemological anomaly that transcends the dogmas of established schools of thought.

The prevailing mindset in medicine is based on a deterministic formalism, according to which variables, events, and data are commutable, and reversing the output data does not alter the result. However, in clinical practice, a critical variable emerges: time. Time establishes an order both in the manifestation of organic damage and in the symptoms of orofacial pain and/or bruxism. This consideration, seemingly logical and trivial, introduces a profound epistemological issue, as it marks the transition from a classical and deterministic statistical model to a quantum and indeterminate model.

Consider the clinical case of a patient suffering from bruxism, detailed in the chapter "Bruxism". The patient reported nocturnal and diurnal bruxism as early as 2000 to his dental colleagues, who intervened with biteplane treatment. In that context, the diagnosis was TMDs, formulated through the RDC model as early as 2000. The colleagues continued to follow the patient until 2014, the year he presented at our Neurognathology Center. During the first phase of experimental research, called "Index $\Psi$ at time $t_{0}$", the diagnosis of bruxism, following the RDC model, was confirmed since the patient met the specific requirements of the model. However, subsequently, at time $t_{n}$ (as previously described), the diagnosis changed to "Pineal Cavernoma".

Suppose that in 2000 the dental colleagues had performed an interferential EMG of the masseters (Figure 1) and, not detecting neuromotor abnormalities (symmetry of amplitudes and discharge frequency of motor units), they would have concluded, of course, that the patient was healthy despite sporadic episodes of bruxism. However, with the intervention in 2014, when we performed the Recovery Cycle of the Masseter Inhibitory Reflex (Figure 2) we revealed severe organic trigeminal neuromotor hyperexcitability, leading to the definitive diagnosis of "Pineal Cavernoma". This shows how, as early as 2000, the organic damage could have been present but the diagnosis changed only in 2014, illustrating the importance of the order of information and the non-commutability of data.

In this exploration, without delving into excessively technical details, we introduce the concept of non-commutative variables and their impact on medical practice.

• 

  Figure 1: Interferential EMG performed in the year 2000. Trace later considered as a quantum operator ${\hat {E}}$

• 

  Figure 2: Recovery Cycle of the Masseter Inhibitory Reflex (rcIMR) performed in the year 2014. Trace later considered as a quantum operator ${\hat {P}}$

Non-commutative Variables

Bayes' Model

As previously mentioned, the Bayes model serves to update the probabilities of diagnosis in light of new evidence. We report the mathematical formalism again to better follow the differences between models:

$P(A|B)={\frac {P(B|A)\cdot P(A)}{P(B)}}$ and only the term $P(B)$ which is crucial for understanding the discussion that follows. This, we repeat, is often called the 'Total Probability Formula'.

Quantum Model

The quantum model employs mathematical operators that can be non-commutative, demonstrating how the order of application of operators can influence the result.

Indeed, the property:

${\hat {A}}{\hat {B}}\neq {\hat {B}}{\hat {A}}$

does not find a direct analogue in the Bayesian model, which does not consider the effect of the order of tests.

Unlike classical models, quantum models can incorporate effects of superposition and interference between states, which are absent in classical probability theory.

Limits of the Bayes Model

The Bayes model does not take into account the order of tests; it simply adds up the evidence without considering how the order might influence the results. Probabilities in the Bayes model are interpreted as measures of uncertainty based on available information, while in quantum mechanics, probabilities also emerge from principles of superposition and non-locality. To distinguish it from the well-known Bayes' Theorem but at the same time differentiate it from Quantum-like models, we might name this approach 'QBism'.

Quantum Bayesianism ‘QBism’

Non-classical models like Bayes provide a perspective based on the principles of quantum mechanics, illustrating how the order of diagnostic tests can influence the results of the diagnosis, exploiting the non-commutativity of quantum operators.

Non-commutativity of Data

Each diagnostic test is modeled as a quantum operator that acts on a state space, representing the different health conditions of the patient.

• EMG Operator ${\hat {E}}$ (see figure 1)
  • Poorly effective for detecting trigeminal neuromotor hyperexcitability.
  • Operator matrix:

${\hat {E}}={\begin{pmatrix}0.95&0.05\\0.05&0.95\end{pmatrix}}$

• Operator _rcIMR ${\hat {P}}$ (see figure 2)
  • Highly effective for detecting trigeminal neuromotor hyperexcitability.
  • Operator matrix:

${\hat {P}}={\begin{pmatrix}0.1&0.9\\0.9&0.1\end{pmatrix}}$

Initial State of the Patient

• The initial state vector of the patient is:

$\psi ={\begin{pmatrix}1\\0\end{pmatrix}}$ This indicates that the patient is initially considered healthy.

Simulation of Results

• Scenario 1: EMG in 2000 followed by the test _rcIMR in 2014
  • Result after EMG:

${\hat {E}}{\begin{pmatrix}1\\0\end{pmatrix}}={\begin{pmatrix}0.95\\0.05\end{pmatrix}}$

This indicates that, after the application of the EMG, the state vector shows a 95% probability that the patient is healthy and only a 5% probability of disease, highlighting the poor sensitivity of the EMG for the pathology in question (Pineal Cavernoma).

• Result after _rcIMR in 2014:

${\hat {P}}{\begin{pmatrix}0.95\\0.05\end{pmatrix}}={\begin{pmatrix}0.14\\0.86\end{pmatrix}}$

This confirms that, numerically, the application of the matrix has transformed the state so that the probability of detecting the disease has increased significantly (from 5% to 86%), highlighting the disease that the EMG had not detected.

• Scenario 2: _rcIMR performed in 2000
  • Immediate result:

${\hat {P}}{\begin{pmatrix}1\\0\end{pmatrix}}={\begin{pmatrix}0.1\\0.9\end{pmatrix}}$ Would have revealed the disease already in 2000.

The simulation clearly shows that the use of the test 'Recovery Cycle of the Masseter Inhibitory Reflex' (_rcIMR) as an initial test in 2000 could have revealed the Pineal Cavernoma immediately, offering the possibility of a diagnosis and intervention 14 years earlier. This underscores the critical importance of the order in which diagnostic tests are performed and the potential impact on patient management. The non-commutativity of operators (diagnostic tests) in medicine can have real and significant implications for diagnosis and treatment of medical conditions.

Classical Probability vs Quantum Probability*

Classical probability (CP) is a mathematically formalized model by Kolmogorov in 1933 and is based on the calculation of probability measures, where a non-negative weight $p(A)$ is assigned to each event. The fundamental characteristic of CP is its additivity: if two events $\alpha$ and $\beta$ are disjoint, the probability of their union is equal to the sum of their individual probabilities:

$P(\alpha \cup \beta )=P(\alpha )+P(\beta )$

In CP, the total probability formula (FTP) is derived using the additivity of probability and the Bayes' formula, to define conditional probability:

$P(B=\beta )=\sum _{\alpha }P(A=\alpha )P(B=\beta \mid A=\alpha )$

Quantum probability (QP), on the other hand, operates with complex probability amplitudes rather than simple probability measures. QP is considered a vectorial model of probabilistic reasoning, where each complex amplitude determines the probability according to the Born rule:

$P=|\psi |^{2}$, where $|\psi |^{2}$ is the square of the modulus of the complex amplitude.

Unlike CP, QP allows the violation of the fundamental laws of CP due to complex probability amplitudes.

In QP, the classical version of the FTP is modified by the interference term. For the quantum observables $A$ and $B$, represented by hermitian operators ${\hat {A}}$ and ${\hat {B}}$, the quantum version of the FTP appears as follows (the formula has been divided into two parts for reasons of space and description):

Part 1:	$\longrightarrow$				$P(B=\beta )=\sum _{\alpha }P(A=\alpha _{1})P(B=\beta \mid A=\alpha _{1})$					$Eq.1$
							$+$
Part 2:	$\longrightarrow$				$2\sum _{\alpha _{1}<\alpha _{2}}\cos \theta _{\alpha _{1}\alpha _{2}}{\sqrt {P(A=\alpha _{1})P(B=\beta \mid A=\alpha _{1})P(A=\alpha _{2})P(B=\beta \mid A=\alpha _{2})}}$

This equation highlights how QP differs significantly from CP, especially in the modulation induced by data interference, offering a new perspective on how the order of diagnostic tests can influence the results.

Data derived from the follow-up at time $t_{n}$

Let's take a more practical clinical view of what happens to our dear data exiting the table

• Total Population: 40 individuals
• Total Symptomatics: 10 individuals
• With Actual TMDs: 9 (number of symptomatic subjects diagnosed by the RDC model)
• With Other Serious Pathologies (non-TMDs): 7 (during the follow-up at time $t_{n}$ by the group of experts, it was verified that among the 10 symptomatic subjects, 7 subjects were affected by serious non-TMD pathologies)
• False Negative (sick but considered healthy): 1 (among the 10 healthy subjects remained as a false negative both in the RDC test and in the verification by the group of experts at time $t_{n}$ the usual subject No. 40)

Test data from table 2 that represent the statistical analysis and Bayes at time $t_{0}$ we have:

• Sensitivity (SE): $90\%\longrightarrow 0.9$
• Specificity (SP): $100\%\longrightarrow 1$

• Prevalence of TMDs among the Symptomatic: $P(A=\alpha _{1})={\frac {9}{10}}=0.9$. This indicates that 9 out of 10 symptomatic individuals were diagnosed as TMDs through the RDC model. This corresponds to a prevalence of $90\%\longrightarrow 0.9$in mathematical terms, in the group of symptomatics. This calculation correctly reflects the proportion of subjects affected by TMDs relative to the total number of symptomatics
• Probability of TMDs: $P(B=\beta \mid A=\alpha _{1})=0.9$ — Probability of being correctly diagnosed as TMDs if you have TMDs (high sensitivity of the test).
• Prevalence of Other Serious Pathologies among the Symptomatic: $P(A=\alpha _{2})={\frac {7}{10}}=0.7$ . This indicates that 7 out of 10 symptomatic individuals were identified with serious pathologies other than TMDs during the follow-up at time $t_{n}$. This represents a prevalence of $70\%\longrightarrow 0.7$in mathematical terms, in the group of symptomatics classified as non-TMDs.
• Probability of non-TMDs:$P(B=\beta \mid A=\alpha _{2})$ Probability of being erroneously diagnosed as TMDs when you have a non-TMD pathology
• Angle $\theta ={\frac {\pi }{1.5}}$: The angle $\theta$ assumes an important significance in this context, namely a difference between the data exiting the experimentation between subjects classified as patients affected by TMDs through the RDC test (quantity 9 out of 10) and those diagnosed at time $t_{n}$ by the group of experts considered sick with serious non-TMD pathologies (7 out of 10). This ratio is therefore quantified as ${\frac {\pi }{1.5}}$ in radians which converted to degrees corresponds to an angle $\theta =120^{\circ }$. The angle $\theta$ represents a mathematical concept that in this specific context is used to quantify the discrepancy between two diagnostic categories within the same group of symptomatic patients: patients with TMDs and those with other serious pathologies (non-TMDs). The choice to represent this discrepancy through an angle and its cosine can be seen as an attempt to apply principles of geometry or physics (such as wave interference) to interpret the complexity of medical diagnoses. Here's how this concept can influence clinical practice:
  • Diagnostic Differentiation: The angle $\theta =120^{\circ }$ and the value of the cosine of $\theta$ ($-0.5$) indicate a distinct separation between the two diagnostic groups in the context of the analysis model. An angle of 120°, which is relatively wide, suggests that the characteristics of patients with TMDs are substantially different from those of patients with other serious pathologies. This can help clinicians consider the importance of not overlapping treatments and refining diagnostic tools to better target therapies.
  • Implications for Diagnosis and Treatment: The interpretation of the angle and cosine can be used to assess how well a diagnostic test distinguishes between these two conditions. If the cosine were close to 1 (or $\theta$ close to 0°), it would indicate that the tests are not making a good distinction between the conditions. Conversely, a negative cosine value indicates a marked distinction, which is crucial to avoid inappropriate or ineffective treatments.
  • Development of Specific Protocols: Understanding the nature of $\theta$ may prompt the development of more specialized diagnostic and therapeutic protocols, improving the effectiveness of treatment for each group of pathologies. This approach is particularly relevant in the medical field where the precision of diagnosis directly affects the success of treatment.

• Cosine of the angle $\theta \longrightarrow$ $\cos(\theta )=-0.5$: Thus, we can interpret $\theta =120^{\circ }$ as the angle that represents this proportion, whose $\cos(\theta )=-0.5$. In this context, the cosine of $\theta$ can be considered as a measure of the discrepancy between $\alpha _{1}$ and $\alpha _{2}$, where higher values of $\cos \theta$ indicate a greater difference between symptomatic subjects sick with TMDs and those non-TMDs

Calculation of the Probability of a True Positive

The probability of a true positive in the RDC test and thus affected by TMDs without considering interference with other diagnosed pathologies at time $t_{n}$ is calculated as:

$P(B={\text{TMDs}}|A=\alpha _{1})=0.9\times 0.9=0.81\longrightarrow 81\%$and to follow the concept of quantum probability more smoothly in eq.1, the first part of the equation will be completed as follows:

$P(B=\beta )=\sum _{\alpha }P(A=\alpha _{1})P(B=\beta \mid A=\alpha _{1})\longrightarrow P(B={\text{TMDs}}|A=\alpha _{1})=0.9\times 0.9=0.81\longrightarrow 81\%$

Calculation of Interference

Interference is calculated using the formula:

${\text{Interference}}=2\times \cos(\theta )\times {\sqrt {P(A=\alpha _{1})\times P(B={\text{TMDs}}|A=\alpha _{1})}}\times {\sqrt {P(A=\alpha _{2})}}\rightarrow$$2\times (-0.5)\times {\sqrt {0.9\times 0.81}}\times {\sqrt {0.7}}\approx -0.7144$

The efficacy of the test, adjusted for interference, is $P(B={\text{TMDs}}|A=\alpha _{\text{TMDs}})+{\text{Interference}}$

This result indicates a drastic reduction in the effectiveness of the diagnostic test when considering interference caused by the coexistence of other pathologies.

We recapitulate succinctly by reporting the quantum probabilities formula $Eq.1$, the numerical data to better understand the meaning of the mathematical procedures and the diagnostic clinical significance derived from it as follows:

$P(B=\beta )=\sum _{\alpha }P(A=\alpha _{1})P(B=\beta \mid A=\alpha _{1})$	$+$	$2\sum _{\alpha _{1}<\alpha _{2}}\cos \theta _{\alpha _{1}\alpha _{2}}{\sqrt {P(A=\alpha _{1})P(B=\beta \mid A=\alpha _{1})P(A=\alpha _{2})P(B=\beta \mid A=\alpha _{2})}}$			$Eq.1$
$P(B=\beta )=\sum _{\alpha }(0.9\times 0.9)$	$+$	$2\times (-0.5)\times {\sqrt {0.9\times 0.81}}\times {\sqrt {0.7}}6\%$			$Eq.2$
$\sum _{\alpha }(0.81)$	$+$	$(-1)\times (0.853)\times (0.836)=0.0956\rightarrow 9.56\%$			$Eq.3$

Conclusion

The diagnosis of Temporomandibular Disorders (TMD) through the RDC model and the use of Bayes' Theorem represents a robust approach that integrates clinical data with advanced statistical principles. However, the complexity of such a diagnosis lies not only in the variability of symptoms but also in the interference of other pathologies that can mimic or aggravate TMD symptoms. The specificity and sensitivity of the diagnostic test, although high, do not exclude the risk of false positives or negatives, even those not represented in the RDC model, highlighting the need for a more holistic and multidisciplinary diagnostic approach.

The probability of a true positive calculated as $P(B={\text{TMDs}}|A=\alpha _{1})=0.9\times 0.9=0.81\longrightarrow 81\%$ shows a high probability that the patient is actually affected by TMD when the test is positive following the RDC model. However, the introduction of the angle $\theta ={\frac {\pi }{1.5}}$ that measures the discrepancy between patients with TMDs and those with other serious non-TMD pathologies conducted in the follow-up by the group of experts, underscores the complexity of using a single diagnostic parameter to differentiate the various clinical conditions.

The calculated interference, which drastically reduces the efficacy of the test to $9.56\%$, raises serious doubts about its utility without adequate consideration of concomitant conditions. This underscores the importance of detailed follow-up and clinical evaluation that does not rely solely on quantitative results.

The Bayes model, although a powerful tool in reformulating diagnostic probabilities, shows its limitations in the field of TMDs due to the complex etiology and clinical presentation of these disorders. The discussion of the quantum model, which considers the non-commutativity of data, opens new perspectives on the management of diagnostic data, suggesting that the order in which tests are performed can significantly alter the interpretation of results. This model offers an innovative approach that could improve diagnostic accuracy, especially in complex clinical scenarios where multiple interactions between various tests and symptoms can alter diagnostic probabilities.

In the future, integrating quantum models along with established diagnostic methods could not only refine our diagnostic capabilities for TMDs but also offer a deeper understanding of the interdependencies between various symptoms and conditions. This would require further studies and validations to ensure that such methods are not only theoretically valid but also practically applicable in the clinical context.

In summary, while the Bayes model continues to be a fundamental pillar in probabilistic analysis in medicine, the adoption of approaches based on quantum mechanics could revolutionize the way we understand and manage complex diseases like TMDs. This emphasizes the importance of a diagnostic approach that is both rigorous and flexible, capable of adapting and integrating new scientific and technological discoveries.

«Are we still sure we know everything?»

Bibliography & references