Difference between revisions of "Store:LTcondilo"
| Line 17: | Line 17: | ||
(Y - latero-mediale) | (Y - latero-mediale) | ||
|- | |- | ||
| rowspan="8" |[[File:Figura 2 finale.jpg|center|400x400px|'''Figura 2:''' Rappresentazione grafica reale dei punti marcati nel ciclo masticatorio]]'''Figura 2''': | | rowspan="8" |[[File:Figura 2 finale mod..jpg|center|400x400px|'''Figura 2:''' Rappresentazione grafica reale dei punti marcati nel ciclo masticatorio]]'''Figura 2''': | ||
|2 | |2 | ||
|1.70 | |1.70 | ||
Revision as of 17:17, 21 December 2024
Distanze e Direzioni
Condilo Laterotrusivo
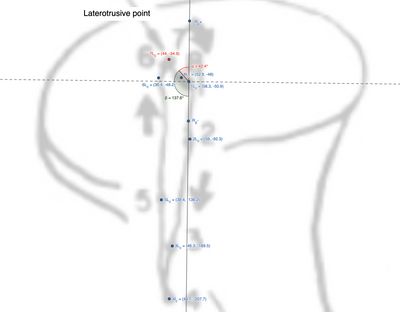
Questo paragrafo illustra un processo matematico utilizzato per calcolare la distanza e l'angolo formato tra due segmenti in un piano 2D, con applicazione nella cinematica mandibolare. La spiegazione riguarda come determinare l'angolo tra due vettori che rappresentano movimenti articolari all'interno di un sistema articolare, ad esempio i condili durante i movimenti della mandibola (Figura 2 e Tabella 1).
| Tabella 1 | ||||
|---|---|---|---|---|
| Tracciato masticatorio | Markers | Distanza (mm) | Direzione
(X - antero-posteriore) |
Direzione dinamica
(Y - latero-mediale) |
| Figura 2: | 2 | 1.70 | Nessuno | Lateralizzazione |
| 3 | 4.93 | Avanti | Lateralizzazione | |
| 4 | 6.57 | Avanti | Lateralizzazione | |
| 5 | 3.51 | Avanti | Lateralizzazione | |
| 6 | 1.07 | Indietro | Medializzazione | |
| 7* | 1.05 | Indietro | Medializzazione | |
| 8 | 0.43 | Indietro | Medializzazione | |
Osservando la figura e la tabella, possiamo estrapolare le distanze dei punti marcati dallo strumento di replicazione dei movimenti mandibolari. Nello specifico, la distanza tra il punto e il punto è stata correttamente calcolata come circa , con una direzione calcolata come:
Per chi desidera approfondire il formalismo matematico, riportiamo il calcolo dettagliato nel popup interattivo.
![]() Dobbiamo calcolare la distanza euclidea tra i punti e . La formula per la distanza euclidea tra due punti e è:
Sostituendo i valori: . A questo punto, per convertire in millimetri, moltiplichiamo la distanza in pixel per il fattore di conversione:
Ora possiamo calcolare l'angolo utilizzando la formula per il coseno dell'angolo tra due vettori:
Infine, l'angolo è calcolato tramite la funzione arccoseno:
Dobbiamo calcolare la distanza euclidea tra i punti e . La formula per la distanza euclidea tra due punti e è:
Sostituendo i valori: . A questo punto, per convertire in millimetri, moltiplichiamo la distanza in pixel per il fattore di conversione:
Ora possiamo calcolare l'angolo utilizzando la formula per il coseno dell'angolo tra due vettori:
Infine, l'angolo è calcolato tramite la funzione arccoseno: