Difference between revisions of "Store:AC36mediotrusivo"
| Line 70: | Line 70: | ||
\theta = \arccos(-0.0232) \approx 91.33^\circ | \theta = \arccos(-0.0232) \approx 91.33^\circ | ||
</math>. Per approfondire la procedura matematica vedi {{Tooltip|2=I tre punti nello spazio 2D sono <math>P1_{mm}</math> (punto 1 del molare mediotrusivo), <math>P7_{mm}</math> (punto 7 del molare mediotrusivo) e <math>R_p</math> (punto di riferimento), con coordinate <math>P1_{mm} = (907.1, -852.5)</math>, <math>P7_{mm} = (817.2, -853.5)</math>, <math>R_p = (908.8, -711.5)</math>. Il vettore tra <math>P1_{mm}</math> e <math>P7_{mm}</math> è <math>\vec{AB} = (-89.9, -1.0)</math>, mentre il vettore tra <math>P1_{mm}</math> e <math>R_p</math> è <math>\vec{AC} = (1.7, 141.0)</math>. Prodotto scalare: <math>\vec{AB} \cdot \vec{AC} = (-89.9) \cdot (1.7) + (-1.0) \cdot (141.0) = -152.83 - 141.0 = -293.83</math>. Norme: <math>|\vec{AB}| = \sqrt{(-89.9)^2 + (-1.0)^2} = \sqrt{8083.01} \approx 89.88</math>, <math>|\vec{AC}| = \sqrt{(1.7)^2 + (141.0)^2} = \sqrt{19883.89} \approx 141.02</math>. Coseno: <math>\cos(\theta) = \frac{\vec{AB} \cdot \vec{AC}}{|\vec{AB}| \cdot |\vec{AC}|} = \frac{-293.83}{89.88 \cdot 141.02} \approx -0.0232</math>.Angolo: <math>\theta = \arccos(-0.0232) \approx 91.33^\circ</math>. Distanza lineare: <math>d = \sqrt{8083.01} \approx 89.88 \, \text{pixel}</math>, convertita in millimetri: <math>d = 89.88 \cdot 0.1 = 8.99 \, \text{mm}</math>.}} | </math>. Per approfondire la procedura matematica vedi {{Tooltip|2=I tre punti nello spazio 2D sono <math>P1_{mm}</math> (punto 1 del molare mediotrusivo), <math>P7_{mm}</math> (punto 7 del molare mediotrusivo) e <math>R_p</math> (punto di riferimento), con coordinate <math>P1_{mm} = (907.1, -852.5)</math>, <math>P7_{mm} = (817.2, -853.5)</math>, <math>R_p = (908.8, -711.5)</math>. Il vettore tra <math>P1_{mm}</math> e <math>P7_{mm}</math> è <math>\vec{AB} = (-89.9, -1.0)</math>, mentre il vettore tra <math>P1_{mm}</math> e <math>R_p</math> è <math>\vec{AC} = (1.7, 141.0)</math>. Prodotto scalare: <math>\vec{AB} \cdot \vec{AC} = (-89.9) \cdot (1.7) + (-1.0) \cdot (141.0) = -152.83 - 141.0 = -293.83</math>. Norme: <math>|\vec{AB}| = \sqrt{(-89.9)^2 + (-1.0)^2} = \sqrt{8083.01} \approx 89.88</math>, <math>|\vec{AC}| = \sqrt{(1.7)^2 + (141.0)^2} = \sqrt{19883.89} \approx 141.02</math>. Coseno: <math>\cos(\theta) = \frac{\vec{AB} \cdot \vec{AC}}{|\vec{AB}| \cdot |\vec{AC}|} = \frac{-293.83}{89.88 \cdot 141.02} \approx -0.0232</math>.Angolo: <math>\theta = \arccos(-0.0232) \approx 91.33^\circ</math>. Distanza lineare: <math>d = \sqrt{8083.01} \approx 89.88 \, \text{pixel}</math>, convertita in millimetri: <math>d = 89.88 \cdot 0.1 = 8.99 \, \text{mm}</math>.}} | ||
---- | |||
==Molare controlaterale== | |||
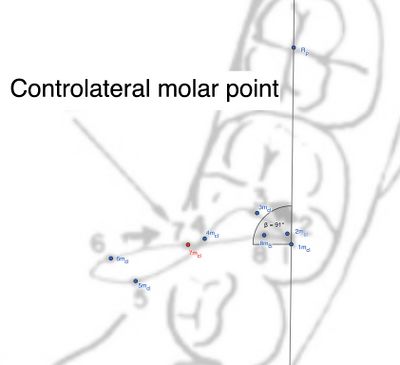
Osservando il moto cinematico mandibolare a livello del molare mediotrusivo, si nota come cambia sia la direzione (angolo rispetto all'asse perpendicolare che interseca il punto 1 del condilo mediotrusivo) sia la medializzazione nel ritorno allo stato iniziale, che corrisponde sostanzialmente allo svincolo mediotrusivo tra la cuspide centrale e distale del primo molare. | |||
<Center> | |||
{| | |||
! colspan="5" |Tabella 4 | |||
|- | |||
!Tracciato masticatorio | |||
!Markers | |||
!Distanza | |||
(mm) | |||
!Direzione in X | |||
(antero-posteriore) | |||
!Direzione | |||
dinamica | |||
(Y -latero-mediale) | |||
|- | |||
| rowspan="11" |[[File:Mediotrusive_Molar_Point_Corrected.jpg|400x400px|center|'''Figura 4:''' ]]'''Figura 4:''' | |||
| | |||
| | |||
| | |||
| | |||
|- | |||
|2||1.11 | |||
|Avanti||Medializzazione | |||
|- | |||
|3||3.89 | |||
|Avanti||Medializzazione | |||
|- | |||
|4||7.76 | |||
|Avanti||Medializzazione | |||
|- | |||
|5||13.75 | |||
|Avanti||Medializzazione | |||
|- | |||
|6||15.71 | |||
|Indietro||Inversione | |||
|- | |||
|7*||8.99 | |||
|Indietro||Lateralizzazione | |||
|- | |||
|8||2.43 | |||
|Indietro||Lateralizzazione | |||
|- | |||
| colspan="4" | | |||
|} | |||
</Center> | |||
<br /> | |||
Come per i precedenti, la distanza lineare tra il punto 1 ed il punto 7* è risultata essere <math>8.99</math> mm e l'angolo <math>\theta</math> è calcolato tramite la funzione arcoseno: <math>\theta = \arccos(-0.0232) \approx 91.33^\circ</math>. | |||
Per approfondire la procedura matematica vedi {{Tooltip|2=I tre punti nello spazio 2D sono <math>P1_{mm}</math> (punto 1 del molare mediotrusivo), <math>P7_{mm}</math> (punto 7 del molare mediotrusivo) e <math>R_p</math> (punto di riferimento), con coordinate <math>P1_{mm} = (422.5, -396.1)</math>, <math>P7_{mm} = (383.8, -395.1)</math>, <math>R_p = (422.7, -336.6)</math>. Il vettore tra <math>P1_{mm}</math> e <math>P7_{mm}</math> è <math>\vec{AB} = (-38.7, 1.0)</math>, mentre il vettore tra <math>P1_{mm}</math> e <math>R_p</math> è <math>\vec{AC} = (0.2, 59.5)</math>. Prodotto scalare: <math>\vec{AB} \cdot \vec{AC} = (-38.7) \cdot (0.2) + (1.0) \cdot (59.5) = -7.74 + 59.5 = 51.76</math>. Norme: <math>|\vec{AB}| = \sqrt{(-38.7)^2 + (1.0)^2} = \sqrt{1498.69 + 1.0} = \sqrt{1499.69} \approx 38.73</math>, <math>|\vec{AC}| = \sqrt{(0.2)^2 + (59.5)^2} = \sqrt{0.04 + 3540.25} = \sqrt{3540.29} \approx 59.54</math>. Coseno: <math>\cos(\theta) = \frac{\vec{AB} \cdot \vec{AC}}{|\vec{AB}| \cdot |\vec{AC}|} = \frac{51.76}{38.73 \cdot 59.54} \approx 0.0226</math>. Angolo: <math>\theta = \arccos(0.0226) \approx 91.33^\circ</math>. Distanza lineare: <math>d = \sqrt{1499.69} \approx 38.73 \, \text{pixel}</math>, convertita in millimetri: <math>d = 38.73 \cdot 0.1 = 8.99 \, \text{mm}</math>.}} | |||
Revision as of 19:30, 13 December 2024
Molare controlaterale
Osservando il moto cinematico mandibolare a livello del molare lediotrusivo possiamo notare come cambia sia la direzione ( angolo rispetto all'asse perpendicolare che interseca il punto 1 del condilo mediotrusivo ma anche la medializzazione nel ritorno allo stato iniziale che sostanzialmente corrisponde allo svincolo mediotrusivo tra la cuspide centrale e distale del primo molare.
| Tabella 4 | ||||
|---|---|---|---|---|
| Tracciato masticatorio | Markers | Distanza
(mm) |
Direzione in X
(antero-posteriore) |
Direzione
dinamica (Y -latero-mediale) |
| Figura 4: | ||||
| 2 | 1.11 | Avanti | Medializzazione | |
| 3 | 3.89 | Avanti | Medializzazione | |
| 4 | 7.76 | Avanti | Medializzazione | |
| 5 | 13.75 | Avanti | Medializzazione | |
| 6 | 15.71 | Indietro | Inversione | |
| 7* | 8.99 | Indietro | Lateralizzazione | |
| 8 | 2.43 | Indietro | Lateralizzazione | |
Come per i precedenti la distanza lineare tra il punto 1 ed il punto 7* è risultata essere mm e l'angolo è calcolato tramite la funzione arcoseno: . Per approfondire la procedura matematica vedi ![]() I tre punti nello spazio 2D sono (punto 1 del molare mediotrusivo), (punto 7 del molare mediotrusivo) e (punto di riferimento), con coordinate , , . Il vettore tra e è , mentre il vettore tra e è . Prodotto scalare: . Norme: , . Coseno: .Angolo: . Distanza lineare: , convertita in millimetri: .
I tre punti nello spazio 2D sono (punto 1 del molare mediotrusivo), (punto 7 del molare mediotrusivo) e (punto di riferimento), con coordinate , , . Il vettore tra e è , mentre il vettore tra e è . Prodotto scalare: . Norme: , . Coseno: .Angolo: . Distanza lineare: , convertita in millimetri: .
Molare controlaterale
Osservando il moto cinematico mandibolare a livello del molare mediotrusivo, si nota come cambia sia la direzione (angolo rispetto all'asse perpendicolare che interseca il punto 1 del condilo mediotrusivo) sia la medializzazione nel ritorno allo stato iniziale, che corrisponde sostanzialmente allo svincolo mediotrusivo tra la cuspide centrale e distale del primo molare.
| Tabella 4 | ||||
|---|---|---|---|---|
| Tracciato masticatorio | Markers | Distanza
(mm) |
Direzione in X
(antero-posteriore) |
Direzione
dinamica (Y -latero-mediale) |
| Figura 4: | ||||
| 2 | 1.11 | Avanti | Medializzazione | |
| 3 | 3.89 | Avanti | Medializzazione | |
| 4 | 7.76 | Avanti | Medializzazione | |
| 5 | 13.75 | Avanti | Medializzazione | |
| 6 | 15.71 | Indietro | Inversione | |
| 7* | 8.99 | Indietro | Lateralizzazione | |
| 8 | 2.43 | Indietro | Lateralizzazione | |
Come per i precedenti, la distanza lineare tra il punto 1 ed il punto 7* è risultata essere mm e l'angolo è calcolato tramite la funzione arcoseno: .
Per approfondire la procedura matematica vedi ![]() I tre punti nello spazio 2D sono (punto 1 del molare mediotrusivo), (punto 7 del molare mediotrusivo) e (punto di riferimento), con coordinate , , . Il vettore tra e è , mentre il vettore tra e è . Prodotto scalare: . Norme: , . Coseno: . Angolo: . Distanza lineare: , convertita in millimetri: .
I tre punti nello spazio 2D sono (punto 1 del molare mediotrusivo), (punto 7 del molare mediotrusivo) e (punto di riferimento), con coordinate , , . Il vettore tra e è , mentre il vettore tra e è . Prodotto scalare: . Norme: , . Coseno: . Angolo: . Distanza lineare: , convertita in millimetri: .