Difference between revisions of "Store:FLit05"
| Line 1: | Line 1: | ||
==Insieme sfocato <math>\tilde{A}</math> e funzione di appartenenza <math>\mu_{\displaystyle {\tilde {A}}}(x)</math>== | ==Insieme sfocato <math>\tilde{A}</math> e funzione di appartenenza <math>\mu_{\displaystyle {\tilde {A}}}(x)</math>== | ||
Scegliamo - come formalismo - di rappresentare un insieme sfocato con la 'tilde':<math>\tilde{A}</math>. Un insieme fuzzy è un insieme in cui gli elementi hanno un 'grado' di appartenenza (coerente con la logica fuzzy): alcuni possono essere inclusi nell'insieme al 100%, altri in percentuali inferiori. | |||
A rappresentare matematicamente questo grado di appartenenza è la funzione <math>\mu_{\displaystyle {\tilde {A}}}(x)</math> chiamata ''''Funzione di appartenenza'''<nowiki/>'. La funzione <math>\mu_{\displaystyle {\tilde {A}}}(x)</math> è una funzione continua definita nell'intervallo <math>[0;1]</math> dove: | |||
*<math>\mu_ {\tilde {A}}(x) = 1\rightarrow </math> se <math>x</math> è totalmente contenuta in <math>A</math> (questi punti sono chiamati 'nucleus', essi indicano i valori ''plausibili'' del predicato ). | |||
*<math>\mu_ {\tilde {A}}(x) = 0\rightarrow </math> se <math>x</math> non è contenuto in <math>A</math> | |||
*<math>0<\mu_ {\tilde {A}}(x) < 1 \;\rightarrow </math> se <math>x</math> è parzialmente contenuto in <math>A</math> (questi punti sono chiamati 'Support' ed indicano i valori possibili del predicato <u>possible</u> predicate values). | |||
La rappresentazione grafica della funzione <math>\mu_{\displaystyle {\tilde {A}}}(x)</math> può essere variato; da quelli con linee lineari (triangolari, trapezoidali) a quelli a forma di campana o 'S' (sigmoidale) come rappresentato in Figura 1, che racchiude l'intero concetto grafico della funzione di appartenenza.<ref>{{Cite book | |||
| autore = Zhang W | | autore = Zhang W | ||
| autore2 = Yang J | | autore2 = Yang J | ||
| Line 53: | Line 54: | ||
[[File:Fuzzy_crisp.svg|alt=|left|thumb|400px|'''Figure 1:''' Types of graphs for the membership function.]] | [[File:Fuzzy_crisp.svg|alt=|left|thumb|400px|'''Figure 1:''' Types of graphs for the membership function.]] | ||
The '''support set''' of a fuzzy set is defined as the zone in which the degree of membership results <math>0<\mu_ {\tilde {A}}(x) < 1</math>; | The '''support set''' of a fuzzy set is defined as the zone in which the degree of membership results <math>0<\mu_ {\tilde {A}}(x) < 1</math>; on the other hand, the '''core''' is defined as the area in which the degree of belonging assumes value <math>\mu_ {\tilde {A}}(x) = 1</math> | ||
The 'Support set' represents the values of the predicate deemed '''possible''', while the 'core' represents those deemed more '''plausible'''. | The 'Support set' represents the values of the predicate deemed '''possible''', while the 'core' represents those deemed more '''plausible'''. | ||
If <math>{A}</math | If <math>{A}</math> represented a set in the ordinary sense of the term or classical language logic previously described, its membership function could assume only the values <math>1</math> or <math>0</math>, <math>\mu_{\displaystyle {{A}}}(x)= 1 \; \lor \;\mu_{\displaystyle {{A}}}(x)= 0</math> depending on whether the element <math>x</math> belongs to the whole or not, as considered. Figure 2 shows a graphic representation of the crisp (rigidly defined) or fuzzy concept of membership, which clearly recalls Smuts's considerations.<ref name=":0">•SMUTS J.C. 1926, [[wikipedia:Holism_and_Evolution|<!--139-->Holism and Evolution]], London: Macmillan.</ref> | ||
Let us go back to the specific case of our Mary Poppins, in which we see a discrepancy between the assertions of the dentist and the neurologist and we look for a comparison between classical logic and fuzzy logic: | Let us go back to the specific case of our Mary Poppins, in which we see a discrepancy between the assertions of the dentist and the neurologist and we look for a comparison between classical logic and fuzzy logic: | ||
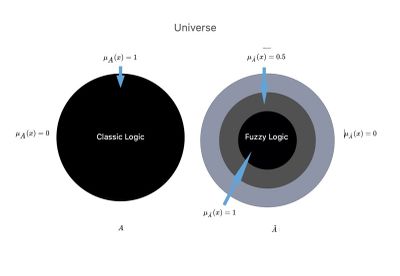
[[File:Fuzzy1.jpg|thumb|400x400px|'''<!--141-->Figure 2:''' <!--142-->Representation of the comparison between a classical and fuzzy ensemble.]] | [[File:Fuzzy1.jpg|thumb|400x400px|'''<!--141-->Figure 2:''' <!--142-->Representation of the comparison between a classical and fuzzy ensemble.]] | ||
'''Figure 2:''' Let us imagine the Science Universe <math>U</math | '''Figure 2:''' Let us imagine the Science Universe <math>U</math> in which there are two parallel worlds or contexts, <math>{A}</math> and <math>\tilde{A}</math>. | ||
<math>{A}=</math> In the scientific context, the so-called ‘crisp’, and we have converted into ''the logic'' of ''Classic Language'', in which the physician has an absolute scientific background information <math>KB</math> | <math>{A}=</math> In the scientific context, the so-called ‘crisp’, and we have converted into ''the logic'' of ''Classic Language'', in which the physician has an absolute scientific background information <math>KB</math> with a clear dividing line that we have named <math>KB_c</math>. | ||
<math>\tilde{A}=</math> In another scientific context called ‘fuzzy logic’, and in which there is a union between the subset <math>{A}</math | <math>\tilde{A}=</math> In another scientific context called ‘fuzzy logic’, and in which there is a union between the subset <math>{A}</math> in <math>\tilde{A}</math> that we can go so far as to say: union between <math>KB_c</math>. | ||
We will remarkably notice the following deductions: | We will remarkably notice the following deductions: | ||
Revision as of 16:40, 30 October 2022
Insieme sfocato e funzione di appartenenza
Scegliamo - come formalismo - di rappresentare un insieme sfocato con la 'tilde':. Un insieme fuzzy è un insieme in cui gli elementi hanno un 'grado' di appartenenza (coerente con la logica fuzzy): alcuni possono essere inclusi nell'insieme al 100%, altri in percentuali inferiori.
A rappresentare matematicamente questo grado di appartenenza è la funzione chiamata 'Funzione di appartenenza'. La funzione è una funzione continua definita nell'intervallo dove:
- se è totalmente contenuta in (questi punti sono chiamati 'nucleus', essi indicano i valori plausibili del predicato ).
- se non è contenuto in
- se è parzialmente contenuto in (questi punti sono chiamati 'Support' ed indicano i valori possibili del predicato possible predicate values).
La rappresentazione grafica della funzione può essere variato; da quelli con linee lineari (triangolari, trapezoidali) a quelli a forma di campana o 'S' (sigmoidale) come rappresentato in Figura 1, che racchiude l'intero concetto grafico della funzione di appartenenza.[1][2]
The support set of a fuzzy set is defined as the zone in which the degree of membership results ; on the other hand, the core is defined as the area in which the degree of belonging assumes value
The 'Support set' represents the values of the predicate deemed possible, while the 'core' represents those deemed more plausible.
If represented a set in the ordinary sense of the term or classical language logic previously described, its membership function could assume only the values or , depending on whether the element belongs to the whole or not, as considered. Figure 2 shows a graphic representation of the crisp (rigidly defined) or fuzzy concept of membership, which clearly recalls Smuts's considerations.[3]
Let us go back to the specific case of our Mary Poppins, in which we see a discrepancy between the assertions of the dentist and the neurologist and we look for a comparison between classical logic and fuzzy logic:
Figure 2: Let us imagine the Science Universe in which there are two parallel worlds or contexts, and .
In the scientific context, the so-called ‘crisp’, and we have converted into the logic of Classic Language, in which the physician has an absolute scientific background information with a clear dividing line that we have named .
In another scientific context called ‘fuzzy logic’, and in which there is a union between the subset in that we can go so far as to say: union between .
We will remarkably notice the following deductions:
- Classical Logic in the Dental Context in which only a logical process that gives as results will be possible, or being the range of data reduced to basic knowledge in the set . This means that outside the dental world there is a void and that term of set theory is written precisely and which is synonymous with a high range of:
- Fuzzy logic in a dental context in which they are represented beyond the basic knowledge of the dental context also those partially acquired from the neurophysiological world will have the prerogative to return a result and a result because of basic knowledge which at this point is represented by the union of dental and neurological contexts. The result of this scientific-clinical implementation of dentistry would allow a «Reduction of differential diagnostic error»
- ↑ Zhang W, Yang J, Fang Y, Chen H, Mao Y, Kumar M, «Analytical fuzzy approach to biological data analysis», in Saudi J Biol Sci, 2017».
PMID:28386181 - PMCID:PMC5372457
DOI:10.1016/j.sjbs.2017.01.027 - ↑ Lazar P, Jayapathy R, Torrents-Barrena J, Mol B, Mohanalin, Puig D, «Fuzzy-entropy threshold based on a complex wavelet denoising technique to diagnose Alzheimer disease», in Healthc Technol Lett, The Institution of Engineering and Technology, 2016».
PMID:30800318 - PMCID:PMC6371778
DOI:10.1049/htl.2016.0022 - ↑ •SMUTS J.C. 1926, Holism and Evolution, London: Macmillan.


![{\displaystyle [0;1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc3bf59a5da5d8181083b228c8933efbda133483)