Difference between revisions of "Store:LTcondilo"
| Line 55: | Line 55: | ||
<math>\theta = 42^\circ </math> | <math>\theta = 42^\circ </math> | ||
Per chi desidera approfondire il formalismo matematico, riportiamo il calcolo dettagliato nel popup interattivo.{{Tooltip|2=<nowiki>Calcolo dettagliato della distanza e dell'angolo: dobbiamo calcolare la distanza euclidea tra i punti \(P_1 = (58.3, -50.9)\) e \(P_7 = (44, -34.9)\). La formula per la distanza euclidea è \(\text{distanza} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\). Sostituendo i valori: \(\text{distanza} = \sqrt{(44 - 58.3)^2 + (-34.9 - (-50.9))^2} = \sqrt{(-14.3)^2 + (16)^2} = \sqrt{204.49 + 256} = \sqrt{460.49} \approx 21.47 \, \text{pixel}\). A questo punto, per convertire in millimetri, moltiplichiamo la distanza per il fattore di scala: \(\text{distanza in mm} = 21.47 \times 0.0418 \approx 1.32 \, \text{mm}\). Ora calcoliamo l'angolo \(\theta\) utilizzando la formula per il coseno: \(\cos(\theta) = \frac{\vec{AB} \cdot \vec{AC {|\vec{AB}| \cdot |\vec{AC}|}\). Considerando i vettori e i calcoli, otteniamo \(\cos(\theta) = 0.789 \implies \theta = 42^\circ \, (\text{arrotondato})\).}}</nowiki>}} | Per chi desidera approfondire il formalismo matematico, riportiamo il calcolo dettagliato nel popup interattivo.{{Tooltip|2=<nowiki>Calcolo dettagliato della distanza e dell'angolo: dobbiamo calcolare la distanza euclidea tra i punti <math>\(P_1 = (58.3, -50.9)\) e \(P_7 = (44, -34.9)\)</math>. La formula per la distanza euclidea è \(\text{distanza} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\). Sostituendo i valori: \(\text{distanza} = \sqrt{(44 - 58.3)^2 + (-34.9 - (-50.9))^2} = \sqrt{(-14.3)^2 + (16)^2} = \sqrt{204.49 + 256} = \sqrt{460.49} \approx 21.47 \, \text{pixel}\). A questo punto, per convertire in millimetri, moltiplichiamo la distanza per il fattore di scala: \(\text{distanza in mm} = 21.47 \times 0.0418 \approx 1.32 \, \text{mm}\). Ora calcoliamo l'angolo \(\theta\) utilizzando la formula per il coseno: \(\cos(\theta) = \frac{\vec{AB} \cdot \vec{AC {|\vec{AB}| \cdot |\vec{AC}|}\). Considerando i vettori e i calcoli, otteniamo \(\cos(\theta) = 0.789 \implies \theta = 42^\circ \, (\text{arrotondato})\).}}</nowiki>}} | ||
Revision as of 17:36, 21 December 2024
Condilo Laterotrusivo
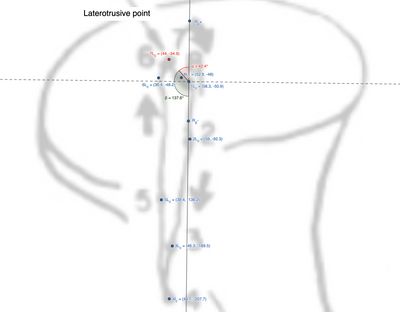
Questo paragrafo illustra un processo matematico per calcolare la distanza e l'angolo formato tra due segmenti in un piano 2D, con applicazione nella cinematica mandibolare. La spiegazione riguarda il calcolo degli angoli tra vettori che rappresentano movimenti articolari, ad esempio i condili durante i movimenti mandibolari (Figura 2 e Tabella 1).
| **Tabella 1: Distanze e direzioni** | ||||
|---|---|---|---|---|
| **Tracciato masticatorio** | **Markers** | **Distanza (mm)** | **Direzione (X - antero-posteriore)** | **Direzione dinamica (Y - latero-mediale)** |
| 2 | 1.74 | Nessuno | Lateralizzazione | |
| 3 | 5.19 | Avanti | Lateralizzazione | |
| 4 | 6.96 | Avanti | Lateralizzazione | |
| 5 | 3.90 | Indietro | Medializzazione | |
| 6 | 0.99 | Indietro | Medializzazione | |
| 7* | 1.32 | Indietro | Medializzazione | |
| 8 | 0.44 | Indietro | Medializzazione | |
Osservando la figura e la tabella, possiamo estrapolare le distanze tra i punti marcati. Ad esempio, la distanza tra il punto e il punto è stata correttamente calcolata come circa con una direzione calcolata come:
Per chi desidera approfondire il formalismo matematico, riportiamo il calcolo dettagliato nel popup interattivo. ![]() Calcolo dettagliato della distanza e dell'angolo: dobbiamo calcolare la distanza euclidea tra i punti <math>\(P_1 = (58.3, -50.9)\) e \(P_7 = (44, -34.9)\)</math>. La formula per la distanza euclidea è \(\text{distanza} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\). Sostituendo i valori: \(\text{distanza} = \sqrt{(44 - 58.3)^2 + (-34.9 - (-50.9))^2} = \sqrt{(-14.3)^2 + (16)^2} = \sqrt{204.49 + 256} = \sqrt{460.49} \approx 21.47 \, \text{pixel}\). A questo punto, per convertire in millimetri, moltiplichiamo la distanza per il fattore di scala: \(\text{distanza in mm} = 21.47 \times 0.0418 \approx 1.32 \, \text{mm}\). Ora calcoliamo l'angolo \(\theta\) utilizzando la formula per il coseno: \(\cos(\theta) = \frac{\vec{AB} \cdot \vec{AC {|\vec{AB}| \cdot |\vec{AC}|}\). Considerando i vettori e i calcoli, otteniamo \(\cos(\theta) = 0.789 \implies \theta = 42^\circ \, (\text{arrotondato})\).}}
Calcolo dettagliato della distanza e dell'angolo: dobbiamo calcolare la distanza euclidea tra i punti <math>\(P_1 = (58.3, -50.9)\) e \(P_7 = (44, -34.9)\)</math>. La formula per la distanza euclidea è \(\text{distanza} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\). Sostituendo i valori: \(\text{distanza} = \sqrt{(44 - 58.3)^2 + (-34.9 - (-50.9))^2} = \sqrt{(-14.3)^2 + (16)^2} = \sqrt{204.49 + 256} = \sqrt{460.49} \approx 21.47 \, \text{pixel}\). A questo punto, per convertire in millimetri, moltiplichiamo la distanza per il fattore di scala: \(\text{distanza in mm} = 21.47 \times 0.0418 \approx 1.32 \, \text{mm}\). Ora calcoliamo l'angolo \(\theta\) utilizzando la formula per il coseno: \(\cos(\theta) = \frac{\vec{AB} \cdot \vec{AC {|\vec{AB}| \cdot |\vec{AC}|}\). Considerando i vettori e i calcoli, otteniamo \(\cos(\theta) = 0.789 \implies \theta = 42^\circ \, (\text{arrotondato})\).}}