Store:AC36mediotrusivo

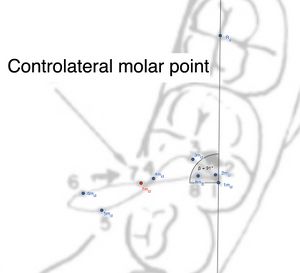
Molare controlaterale

Distanza dei punti in millimetri e direzioni

Punto	Distanza (mm)	Direzione in X (antero-posteriore)	Direzione in Y (latero-mediale)
2	1.11	Avanti	Laterale
3	3.89	Avanti	Laterale
4	7.76	Avanti	Laterale
5	13.75	Avanti	Laterale
6	15.71	Indietro	Laterale
7*	8.99	Indietro	Laterale
8	2.43	Indietro	Laterale

Come per i precedenti la distanza lineare tra il punto 1 ed il punto 7* è risultata essere $8.99$ mm e l'angolo $\theta$ è calcolato tramite la funzione arcoseno: $\theta =\arccos(-0.0232)\approx 91.33^{\circ }$. Per approfondire la procedura matematica vedi  I tre punti nello spazio 2D sono $P1_{mm}$ (punto 1 del molare mediotrusivo), $P7_{mm}$ (punto 7 del molare mediotrusivo) e $R_{p}$ (punto di riferimento), con coordinate $P1_{mm}=(907.1,-852.5)$, $P7_{mm}=(817.2,-853.5)$, $R_{p}=(908.8,-711.5)$. Il vettore tra $P1_{mm}$ e $P7_{mm}$ è ${\vec {AB}}=(-89.9,-1.0)$, mentre il vettore tra $P1_{mm}$ e $R_{p}$ è ${\vec {AC}}=(1.7,141.0)$. Prodotto scalare: ${\vec {AB}}\cdot {\vec {AC}}=(-89.9)\cdot (1.7)+(-1.0)\cdot (141.0)=-152.83-141.0=-293.83$. Norme: $|{\vec {AB}}|={\sqrt {(-89.9)^{2}+(-1.0)^{2}}}={\sqrt {8083.01}}\approx 89.88$, $|{\vec {AC}}|={\sqrt {(1.7)^{2}+(141.0)^{2}}}={\sqrt {19883.89}}\approx 141.02$. Coseno: $\cos(\theta )={\frac {{\vec {AB}}\cdot {\vec {AC}}}{|{\vec {AB}}|\cdot |{\vec {AC}}|}}={\frac {-293.83}{89.88\cdot 141.02}}\approx -0.0232$.Angolo: $\theta =\arccos(-0.0232)\approx 91.33^{\circ }$. Distanza lineare: $d={\sqrt {8083.01}}\approx 89.88\,{\text{pixel}}$, convertita in millimetri: $d=89.88\cdot 0.1=8.99\,{\text{mm}}$.

Conclusione della cinematica del molare mediotrusivo*

L'analisi del movimento articolare del molare controlaterale, sul lato mediotrusivo, rivela informazioni importanti sulla dinamica e sull'adattamento del molare durante i movimenti masticatori laterali. Calcolando le distanze e gli angoli tra punti chiave con l'uso della trigonometria vettoriale, è possibile ottenere una rappresentazione dettagliata del comportamento biomeccanico e della stabilità del molare controlaterale in relazione al movimento mandibolare.

Le distanze lineari tra i punti, riportate in millimetri, evidenziano una complessa sequenza di spostamenti in direzione antero-posteriore e latero-mediale. In particolare, il movimento del molare è influenzato dalla posizione e dalla traiettoria del condilo controlaterale, con transizioni tra avanzamenti e arretramenti che riflettono il percorso anatomico e le influenze muscolari che guidano il movimento.

Dal punto di vista angolare, il calcolo dell'angolo di circa 91.33° indica un movimento quasi perpendicolare rispetto ai segmenti di riferimento, suggerendo che il molare controlaterale mantiene una posizione relativamente stabile rispetto all'asse antero-posteriore durante il movimento mediotrusivo. Un angolo così vicino ai 90° può essere indicativo di un bilanciamento tra le forze che agiscono sul molare, assicurando la necessaria stabilità laterale e contribuendo alla funzione masticatoria in modo ottimale.

Questa analisi matematica del molare controlaterale fornisce un quadro chiaro delle dinamiche masticatorie che influenzano questo punto specifico. L'applicazione del prodotto scalare e del calcolo vettoriale per determinare angoli e distanze supporta una comprensione più profonda delle interazioni articolari, essenziale per identificare eventuali disfunzioni e per guidare i trattamenti di riabilitazione. I risultati di questa analisi non solo contribuiscono alla diagnosi e alla gestione dei disturbi temporomandibolari, ma possono anche migliorare la pianificazione terapeutica nei casi in cui è richiesta una stabilizzazione o una correzione della funzione masticatoria.