Difference between revisions of "Store:MTcondilo"
| Line 24: | Line 24: | ||
|3||148.05||14.81||Indietro||Mediale | |3||148.05||14.81||Indietro||Mediale | ||
|- | |- | ||
|4 | |4||255.81||25.58||Indietro||Mediale | ||
| 255.81||25.58||Indietro||Mediale | |||
|- | |- | ||
|5||265.43||26.54||Indietro||Mediale | |5||265.43||26.54||Indietro||Mediale | ||
|- | |- | ||
|6||145.68||14.57||Indietro|| Mediale | |6||145.68||14.57||Indietro||Mediale | ||
|- | |- | ||
|7*||62.45||6.25|| Indietro||Mediale | |7*||62.45||6.25||Indietro||Mediale | ||
|- | |- | ||
|8||11.87||1.19||Indietro||Mediale | |8||11.87||1.19||Indietro||Mediale | ||
| Line 38: | Line 37: | ||
====Iter matematico per il calcolo dell'angolo==== | ====Iter matematico per il calcolo dell'angolo==== | ||
L'angolo tra due segmenti può essere calcolato utilizzando la la {{Tooltip|trigonometria vettoriale|Innanzitutto, dobbiamo calcolare i vettori che rappresentano i segmenti tra i punti: | L'angolo tra due segmenti può essere calcolato utilizzando la la la {{Tooltip|trigonometria vettoriale|Innanzitutto, dobbiamo calcolare i vettori che rappresentano i segmenti tra i punti: | ||
* Il vettore tra il punto <math>P1_{M}</math> e il punto <math>P7_{M}</math>: <math>\vec{AB} = P7_{M} - P1_{M} = (1148.2, -124.6) - (1164.1, -64.2) = (-15.9, -60.4)</math> | * Il vettore tra il punto <math>P1_{M}</math> e il punto <math>P7_{M}</math>: <math>\vec{AB} = P7_{M} - P1_{M} = (1148.2, -124.6) - (1164.1, -64.2) = (-15.9, -60.4)</math> | ||
* Il vettore tra il punto <math>P1_{M}</math> e il punto <math>H3_{M}</math>: <math>\vec{AC} = H3_{M} - P1_{M} = (1165, 11.4) - (1164.1, -64.2) = (0.9, 75.6)</math> | * Il vettore tra il punto <math>P1_{M}</math> e il punto <math>H3_{M}</math>: <math>\vec{AC} = H3_{M} - P1_{M} = (1165, 11.4) - (1164.1, -64.2) = (0.9, 75.6)</math> | ||
Questo metodo ci permette di rappresentare le relazioni angolari tra movimenti disti ed nell ed ed o | Questo metodo ci permette di rappresentare le relazioni angolari tra movimenti disti ed nell ed ed o ed il {{Tooltip|il Prodotto scalare|Il prodotto scalare tra due vettori \(\vec{AB}\) e \(\vec{AC}\) è dato dalla formula: | ||
<math>\vec{AB} \cdot \vec{AC} = AB_x \cdot AC_x + AB_y \cdot AC_y</math> | <math>\vec{AB} \cdot \vec{AC} = AB_x \cdot AC_x + AB_y \cdot AC_y</math> | ||
| Line 49: | Line 48: | ||
Sostituendo i valori calcolati: | Sostituendo i valori calcolati: | ||
<math>\vec{AB} \cdot \vec{AC} = (-15.9) \cdot (0.9) + (-60.4) \cdot (75.6) = -14.31 - 4566.24 Una volta eseguiti i passaggi trigonometrici | <math>\vec{AB} \cdot \vec{AC} = (-15.9) \cdot (0.9) + (-60.4) \cdot (75.6) = -14.31 - 4566.24 Una volta eseg Una volta eseguiti i passaggi trigonometrici e il prodotto scalare, si passa al calcolo della della {{Tooltip|norma|La norma (o lunghezza) di ciascun vettore è calcolata utilizzando la formula della lunghezza del vettore:}} | ||
<math>|\vec{AB}| = \sqrt{AB_x^2 + AB_y^2} = \sqrt{(-15.9)^2 + (-60.4)^2} = \sqrt{252.81 + 3648.16} = \sqrt{3900.97} \appr | <math>|\vec{AB}| = \sqrt{AB_x^2 + AB_y^2} = \sqrt{(-15.9)^2 + (-60.4)^2} = \sqrt{252.81 + 3648.16} = \sqrt{3900.97} \appr | ||
Ora possiamo usare la formula per il zza) di ciascun vettore è calcolata utilizzando la formula della lu | Ora possiamo usare la formula per il zza) di ciascun vettore è calcolata utilizzando la formula della lu | ||
Ora possiamo usare la formula | |||
Ora possiamo usare la formula per il {{Tooltip|coseno dell'angolo tra i due vettori|: | Ora possiamo usare la formula per il {{Tooltip|coseno dell'angolo tra i due vettori|: | ||
<math>\cos(\theta) = \frac{\vec{AB} \cdot \vec{AC}}{|\vec{AB}| \cdot |\vec{AC}|}</math>. Sostituendo i valori: | <math>\cos(\theta) = \frac{\vec{AB} \cdot \vec{AC}}{|\vec{AB}| \cdot |\vec{AC}|}</math>. Sostituendo i valori: <math>\cos(\theta) = \frac{-4580.55}{62.45 \cdot 75.58} = \frac{-4580.55}{4717.25} \approx -0.971</math>.|2}} | ||
L'angolo <math>\theta</math> è calcolato tramite la funzione arccoseno: | L'angolo <math>\theta</math> è calcolato tramite la funzione arccoseno: | ||
<math>\theta = \arccos(-0.971)</math> | <math>\theta = \arccos(-0.971)</math> | ||
| Line 133: | Line 66: | ||
<math> | <math> | ||
\theta = \arccos(-0.971) \approx 166.43^\circ | \theta = \arccos(-0.971) \approx 166.43^\circ | ||
</math> | </math> Questo angolo sottraendolo a <math> | ||
180^\circ | |||
</math>corrispo ad un angolo di <math> | |||
13.57^\circ | |||
</math> che i dentisti conoscono come '''Angolo di Bennett'''. | |||
==Conclusione della Cinematica Condilare Mediortusiva== | ==Conclusione della Cinematica Condilare Mediortusiva== | ||
Revision as of 16:38, 1 November 2024
Mediotrusive
Descrizione focalizzata dell'analisi matematica dei punti
Punti e coordinate coinvolte
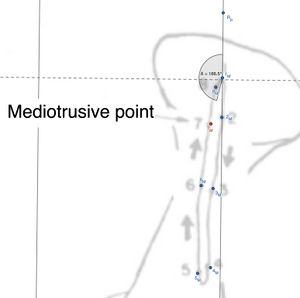
Nel contesto della nostra analisi, abbiamo tre punti nello spazio 2D che ci interessano:
- Coordinate del punto 1 del condilo mediotrusivo:
- Coordinate del punto 7 del condilo mediotrusivo:
- Coordinate del punto di riferimento del condilo mediotrusivo:
Questi punti rappresentano tre posizioni specifiche all'interno di un sistema articolare che stiamo studiando, con l'obiettivo di calcolare l'angolo tra il segmento che unisce i punti e , e il segmento che unisce i punti e . Questo tipo di analisi è comune nella modellazione di movimenti articolari per comprendere come si muovono i segmenti di un sistema rispetto a un punto di riferimento, come nel caso di un sistema masticatorio.
| Punto | Distanza (pixel) | Distanza (mm) | Direzione in X (antero-posteriore) | Direzione in Y (latero-mediale) |
|---|---|---|---|---|
| 2 | 50.92 | 5.09 | Indietro | Mediale |
| 3 | 148.05 | 14.81 | Indietro | Mediale |
| 4 | 255.81 | 25.58 | Indietro | Mediale |
| 5 | 265.43 | 26.54 | Indietro | Mediale |
| 6 | 145.68 | 14.57 | Indietro | Mediale |
| 7* | 62.45 | 6.25 | Indietro | Mediale |
| 8 | 11.87 | 1.19 | Indietro | Mediale |
Iter matematico per il calcolo dell'angolo
L'angolo tra due segmenti può essere calcolato utilizzando la la la {{Tooltip|trigonometria vettoriale|Innanzitutto, dobbiamo calcolare i vettori che rappresentano i segmenti tra i punti:
- Il vettore tra il punto e il punto :
- Il vettore tra il punto e il punto :
Questo metodo ci permette di rappresentare le relazioni angolari tra movimenti disti ed nell ed ed o ed il il Prodotto scalareIl prodotto scalare tra due vettori \(\vec{AB}\) e \(\vec{AC}\) è dato dalla formula:
Sostituendo i valori calcolati:
Failed to parse (syntax error): {\displaystyle \vec{AB} \cdot \vec{AC} = (-15.9) \cdot (0.9) + (-60.4) \cdot (75.6) = -14.31 - 4566.24 Una volta eseg Una volta eseguiti i passaggi trigonometrici e il prodotto scalare, si passa al calcolo della della {{Tooltip|norma|La norma (o lunghezza) di ciascun vettore è calcolata utilizzando la formula della lunghezza del vettore:}} <math>|\vec{AB}| = \sqrt{AB_x^2 + AB_y^2} = \sqrt{(-15.9)^2 + (-60.4)^2} = \sqrt{252.81 + 3648.16} = \sqrt{3900.97} \appr Ora possiamo usare la formula per il zza) di ciascun vettore è calcolata utilizzando la formula della lu Ora possiamo usare la formula Ora possiamo usare la formula per il {{Tooltip|coseno dell'angolo tra i due vettori|: <math>\cos(\theta) = \frac{\vec{AB} \cdot \vec{AC}}{|\vec{AB}| \cdot |\vec{AC}|}} . Sostituendo i valori: .
L'angolo è calcolato tramite la funzione arccoseno:
Infine, l'angolo è calcolato tramite la funzione arcoseno:
Questo angolo sottraendolo a corrispo ad un angolo di che i dentisti conoscono come Angolo di Bennett.
Conclusione della Cinematica Condilare Mediortusiva
Nel sistema masticatorio, il condilo mediotrusivo segue una traiettoria complessa che contribuisce all'equilibrio dinamico durante i movimenti mandibolari laterali. I punti analizzati , e il punto di riferimento rappresentano posizioni articolari chiave lungo il tragitto del condilo mediotrusivo. Studiare questi punti permette di calcolare l'angolo tra due segmenti definiti, essenziali per comprendere i vettori di forza e l'orientamento della mandibola in movimento. In sintesi, l’angolo calcolato tra i punti analizzati del condilo mediotrusivo non solo rappresenta un parametro meccanico, ma funge da indicatore di stabilità e simmetria del sistema masticatorio. Le variazioni angolari rispetto al valore fisiologico suggeriscono l’esistenza di forze anomale o alterazioni che possono influenzare la cinematica mandibolare e potenzialmente contribuire a patologie articolari, offrendo un potenziale punto di osservazione per diagnosi più accurate e interventi clinici mirati.