Difference between revisions of "Store:FLit05"
| Line 54: | Line 54: | ||
[[File:Fuzzy_crisp.svg|alt=|left|thumb|400px|'''Figure 1:''' Types of graphs for the membership function.]] | [[File:Fuzzy_crisp.svg|alt=|left|thumb|400px|'''Figure 1:''' Types of graphs for the membership function.]] | ||
Il '''support set''' di un insieme fuzzy è definito come la zona in cui il grado di appartenenza risulta <math>0<\mu_ {\tilde {A}}(x) < 1</math>; il nucleo o core è invece definito come l'area in cui il grado di appartenenza assume valore <math>\mu_ {\tilde {A}}(x) = 1</math> | |||
Il 'Support set' rappresenta i valori del predicato ritenuti '''possibili''', mentre il 'core' rappresenta quelli ritenuti più '''plausibili'''. | |||
Se <math>{A}</math> rappresentasse un insieme nel senso ordinario del termine o nella logica del linguaggio classico precedentemente descritto, la sua funzione di appartenenza potrebbe assumere solo i valori <math>1</math> o <math>0</math>, <math>\mu_{\displaystyle {{A}}}(x)= 1 \; \lor \;\mu_{\displaystyle {{A}}}(x)= 0</math> a seconda che l'elemento 0 appartenga o meno al tutto, come considerato. La figura 2 mostra una rappresentazione grafica del concetto nitido (rigidamente definito) o sfocato di appartenenza, che richiama chiaramente le considerazioni di Smuts.<ref name=":0">•SMUTS J.C. 1926, [[wikipedia:Holism_and_Evolution|<!--139-->Holism and Evolution]], London: Macmillan.</ref> | |||
Torniamo al caso specifico della nostra Mary Poppins, in cui vediamo una discrepanza tra le affermazioni del dentista e del neurologo e cerchiamo un confronto tra logica classica e logica fuzzy: | |||
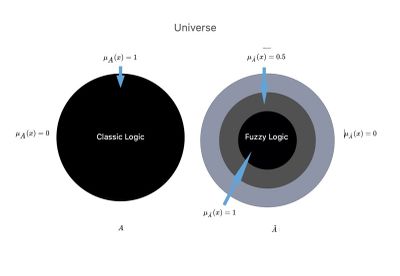
[[File:Fuzzy1.jpg|thumb|400x400px|'''<!--141-->Figure 2:''' <!--142-->Representation of the comparison between a classical and fuzzy ensemble.]] | [[File:Fuzzy1.jpg|thumb|400x400px|'''<!--141-->Figure 2:''' <!--142-->Representation of the comparison between a classical and fuzzy ensemble.]] | ||
''' | '''Figura 2''': Immaginiamo l'Universo della Scienza <math>U</math> in cui ci sono due mondi o contesti paralleli <math>{A}</math> e <math>\tilde{A}</math> | ||
<math>{A}=</math> | <math>{A}=</math> Nel contesto scientifico, il cosiddetto 'ben definito', della logica del linguaggio classico, in cui il medico ha un background scientifico assoluto <math>KB</math> con una chiara linea di demarcazione che abbiamo chiamato <math>KB_c</math> | ||
<math>\tilde{A}=</math> In un altro contesto scientifico chiamato 'logica fuzzy', in cui esiste un'unione tra il sottoinsieme <math>{A}</math> in <math>\tilde{A}</math> tanto da poter dire: unione tra i contesti <math>KB_c</math> | |||
Noteremo notevolmente le seguenti deduzionii: | |||
{{q2| | * '''Logica classica''' nel contesto odontoiatrico <math>{A}</math> in cui sarà possibile solo un processo logico che dia come risultato <math>\mu_{\displaystyle {{A}}}(x)= 1 </math>, ovvero <math>\mu_{\displaystyle {{A}}}(x)= 0 </math> essendo l'intervallo di dati <math>D=\{\delta_1,\dots,\delta_4\}</math> ridotto alle conoscenze di base <math>KB</math> nell'insieme <math>{A}</math> Ciò significa che al di fuori del mondo odontoiatrico c'è un vuoto e che il termine di teoria degli insiemi è scritto esattamente <math>\mu_{\displaystyle {{A}}}(x)= 0 </math> e che è sinonimo di un alto range di: | ||
{{q2|Errore nella diagnosi differenziale|}} | |||
*''' | *'''Logica fuzzy''' in un contesto odontoiatrico <math>\tilde{A}</math> in cui sono rappresentati oltre le conoscenze di base <math>KB</math> del contesto odontoiatrico anche quelli parzialmente acquisiti dal mondo neurofisiologico <math>0<\mu_ {\tilde {A}}(x) < 1</math> avranno la prerogativa di restituire un risultato <math>\mu_\tilde{A}(x)= 1 | ||
</math> | </math> e un risultato 0 per via delle conoscenze di base 0 che a questo punto è rappresentato dall'unione di <math>0<\mu_ {\tilde {A}}(x) < 1</math> contesti odontoiatrici e neurologici. Il risultato di questa implementazione scientifico-clinica dell'odontoiatria consentirebbe una {{q2|Riduzione dell'errore diagnostico differenziale|}} | ||
Latest revision as of 17:31, 30 October 2022
Insieme sfocato e funzione di appartenenza
Scegliamo - come formalismo - di rappresentare un insieme sfocato con la 'tilde':. Un insieme fuzzy è un insieme in cui gli elementi hanno un 'grado' di appartenenza (coerente con la logica fuzzy): alcuni possono essere inclusi nell'insieme al 100%, altri in percentuali inferiori.
A rappresentare matematicamente questo grado di appartenenza è la funzione chiamata 'Funzione di appartenenza'. La funzione è una funzione continua definita nell'intervallo dove:
- se è totalmente contenuta in (questi punti sono chiamati 'nucleus', essi indicano i valori plausibili del predicato ).
- se non è contenuto in
- se è parzialmente contenuto in (questi punti sono chiamati 'Support' ed indicano i valori possibili del predicato possible predicate values).
La rappresentazione grafica della funzione può essere variato; da quelli con linee lineari (triangolari, trapezoidali) a quelli a forma di campana o 'S' (sigmoidale) come rappresentato in Figura 1, che racchiude l'intero concetto grafico della funzione di appartenenza.[1][2]
Il support set di un insieme fuzzy è definito come la zona in cui il grado di appartenenza risulta ; il nucleo o core è invece definito come l'area in cui il grado di appartenenza assume valore
Il 'Support set' rappresenta i valori del predicato ritenuti possibili, mentre il 'core' rappresenta quelli ritenuti più plausibili.
Se rappresentasse un insieme nel senso ordinario del termine o nella logica del linguaggio classico precedentemente descritto, la sua funzione di appartenenza potrebbe assumere solo i valori o , a seconda che l'elemento 0 appartenga o meno al tutto, come considerato. La figura 2 mostra una rappresentazione grafica del concetto nitido (rigidamente definito) o sfocato di appartenenza, che richiama chiaramente le considerazioni di Smuts.[3]
Torniamo al caso specifico della nostra Mary Poppins, in cui vediamo una discrepanza tra le affermazioni del dentista e del neurologo e cerchiamo un confronto tra logica classica e logica fuzzy:
Figura 2: Immaginiamo l'Universo della Scienza in cui ci sono due mondi o contesti paralleli e
Nel contesto scientifico, il cosiddetto 'ben definito', della logica del linguaggio classico, in cui il medico ha un background scientifico assoluto con una chiara linea di demarcazione che abbiamo chiamato
In un altro contesto scientifico chiamato 'logica fuzzy', in cui esiste un'unione tra il sottoinsieme in tanto da poter dire: unione tra i contesti
Noteremo notevolmente le seguenti deduzionii:
- Logica classica nel contesto odontoiatrico in cui sarà possibile solo un processo logico che dia come risultato , ovvero essendo l'intervallo di dati ridotto alle conoscenze di base nell'insieme Ciò significa che al di fuori del mondo odontoiatrico c'è un vuoto e che il termine di teoria degli insiemi è scritto esattamente e che è sinonimo di un alto range di:
- Logica fuzzy in un contesto odontoiatrico in cui sono rappresentati oltre le conoscenze di base del contesto odontoiatrico anche quelli parzialmente acquisiti dal mondo neurofisiologico avranno la prerogativa di restituire un risultato e un risultato 0 per via delle conoscenze di base 0 che a questo punto è rappresentato dall'unione di contesti odontoiatrici e neurologici. Il risultato di questa implementazione scientifico-clinica dell'odontoiatria consentirebbe una «Riduzione dell'errore diagnostico differenziale»
- ↑ Zhang W, Yang J, Fang Y, Chen H, Mao Y, Kumar M, «Analytical fuzzy approach to biological data analysis», in Saudi J Biol Sci, 2017».
PMID:28386181 - PMCID:PMC5372457
DOI:10.1016/j.sjbs.2017.01.027 - ↑ Lazar P, Jayapathy R, Torrents-Barrena J, Mol B, Mohanalin, Puig D, «Fuzzy-entropy threshold based on a complex wavelet denoising technique to diagnose Alzheimer disease», in Healthc Technol Lett, The Institution of Engineering and Technology, 2016».
PMID:30800318 - PMCID:PMC6371778
DOI:10.1049/htl.2016.0022 - ↑ •SMUTS J.C. 1926, Holism and Evolution, London: Macmillan.


![{\displaystyle [0;1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc3bf59a5da5d8181083b228c8933efbda133483)