Difference between revisions of "Store:LPLfr04"
Gianfranco (talk | contribs) (Created page with "==Probabilistic-causal analysis== From these premises it is clear that the clinical diagnosis is made using the so-called hypothetical-deductive method referred to as DN<ref name=":1">{{Cite book | autore = Sarkar S | titolo = Nagel on Reduction | url = https://pubmed.ncbi.nlm.nih.gov/26386529/ | volume = | opera = Stud Hist Philos Sci | anno = 2015 | editore = | città = | ISBN = | PMID = 26386529 | PMCID = | DOI = 10.1016/j.shpsa.2015.05.006 | oaf...") |
|||
| Line 1: | Line 1: | ||
== | ==Analyse probabiliste-causale== | ||
De ces prémisses, il est clair que le diagnostic clinique est effectué en utilisant la méthode dite hypothético-déductive appelée DN<ref name=":1">{{Cite book | |||
| autore = Sarkar S | | autore = Sarkar S | ||
| titolo = Nagel on Reduction | | titolo = Nagel on Reduction | ||
| Line 16: | Line 16: | ||
| LCCN = | | LCCN = | ||
| OCLC = | | OCLC = | ||
}}</ref> ([[wikipedia:Deductive-nomological_model|deductive-nomological model]]<ref>''<!--52-->DN model of scientific explanation'', <!--53-->also known as ''<!--54-->Hempel's model'', ''Hempel–Oppenheim model'', ''Popper–Hempel model'', <!--55-->or ''<!--56-->covering law model''</ref>). | }}</ref> ([[wikipedia:Deductive-nomological_model|deductive-nomological model]]<ref>''<!--52-->DN model of scientific explanation'', <!--53-->also known as ''<!--54-->Hempel's model'', ''Hempel–Oppenheim model'', ''Popper–Hempel model'', <!--55-->or ''<!--56-->covering law model''</ref>). Mais ce n'est pas réaliste, car les connaissances médicales utilisées dans la prise de décision clinique ne contiennent guère de lois déterministes causales pour permettre des explications causales et, par conséquent, pour formuler des diagnostics cliniques, entre autres dans le contexte spécialisé. Essayons d'analyser à nouveau le cas de notre Mary Poppins, en essayant cette fois une approche probabiliste-causale. Considérons un nombre <math>n</math> d'individus, y compris les personnes qui signalent une douleur orofaciale qui ont généralement une dégénérescence osseuse de l'articulation temporo-mandibulaire. Cependant, il peut également y avoir d'autres causes apparemment sans rapport. Nous devons traduire mathématiquement la « pertinence » que ces incertitudes causales ont dans la détermination d'un diagnostic. | ||
===La pertinence décontractée=== | |||
Pour ce faire on considère le degré de pertinence causale <math>(cr)</math> d'un événement <math>E_1</math> par rapport à un événement <math>E_2</math> où : | |||
*<math>E_1</math> = patients atteints de dégénérescence osseuse de l'articulation temporo-mandibulaire | |||
*<math>E_2</math> = patients signalant des douleurs bucco-faciales | |||
*<math> | *<math>E_3</math> =patients sans dégénérescence osseuse de l'articulation temporo-mandibulaire | ||
Nous utiliserons la probabilité conditionnelle <math>P(A \mid B)</math>, c'est-à-dire la probabilité que l'événement <math>A</math> ne se produise qu'après que l'événement <math>B</math> se soit déjà produit. Avec ces prémisses, la pertinence causale <math>cr</math> de l'échantillon <math>n</math> de patients est : | |||
<math>cr=P(E_2 \mid E_1)- P(E_2 \mid E_3)</math> | <math>cr=P(E_2 \mid E_1)- P(E_2 \mid E_3)</math> | ||
où | |||
:<math>P(E_2 \mid E_1)</math> | :<math>P(E_2 \mid E_1)</math> indique la probabilité que certaines personnes (parmi <math>n</math> prises en compte) souffrent de Douleurs Orofaciales causées par la dégénérescence osseuse de l'articulation temporo-mandibulaire, | ||
:alors que | |||
: | |||
:<math>P(E_2 \mid E_3)</math> indique la probabilité que d'autres personnes (toujours parmi <math>n</math> pris en considération) souffrent de Douleur Orofaciale conditionnée par autre chose qu'une dégénérescence osseuse de l'articulation temporo-mandibulaire. | |||
* | :Étant donné que toutes les probabilités suggèrent que <math>P(A \mid B)</math> est une valeur comprise entre <math>0 </math> et <math>1 </math>, le paramètre <math>(cr)</math> sera un nombre compris entre <math>-1 </math> et <math>1 </math>. | ||
:Les significations que nous pouvons donner à ce nombre sont les suivantes: | |||
*on a les cas extrêmes (qui en réalité ne se produisent jamais) qui sont : | |||
:*<math>cr=1</math> | :*<math>cr=1</math>indiquant que la seule cause de douleur orofaciale est la dégénérescence osseuse de l'ATM, | ||
:*<math>cr=-1</math> | :*<math>cr=-1</math> ce qui indique que la cause de la douleur orofaciale n'est jamais une dégénérescence osseuse de l'ATM mais autre chose, | ||
:*<math>cr=0</math> | :*<math>cr=0</math> indiquant que la probabilité que la douleur orofaciale soit causée par une dégénérescence osseuse de l'ATM ou autrement est exactement la même, | ||
* | *et les cas intermédiaires (qui sont les cas réalistes) | ||
:*<math>cr>0</math> | :*<math>cr>0</math> indiquant que la cause de la douleur orofaciale est plus susceptible d'être une dégénérescence osseuse de l'ATM, | ||
:*<math>cr<0</math> | :*<math>cr<0</math> ce qui indique que la cause de la douleur orofaciale n'est probablement pas la dégénérescence osseuse de l'ATM. | ||
<center> | <center> | ||
=== | ===Deuxième approche clinique=== | ||
''( | ''(survolez les images)'' | ||
<gallery widths="350" heights="282" perrow="2" mode="slideshow"> | <gallery widths="350" heights="282" perrow="2" mode="slideshow"> | ||
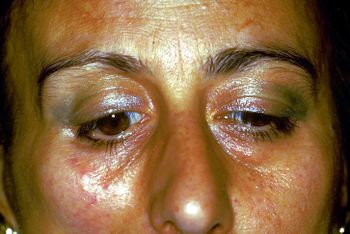
File:Spasmo emimasticatorio.jpg|''' | File:Spasmo emimasticatorio.jpg|'''Figure 1:''' Patient signalant une « douleur orofaciale dans l'hémilatéral droit » | ||
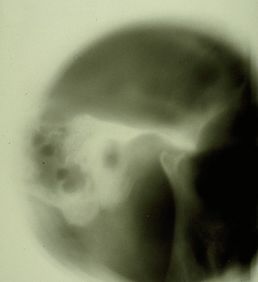
File:Spasmo emimasticatorio ATM.jpg|'''<!--83-->Figure 2:''' | File:Spasmo emimasticatorio ATM.jpg|'''<!--83-->Figure 2:'''Stratigraphie de l'ATM du patient montrant des signes d'aplatissement condylien et d'ostéophyte | ||
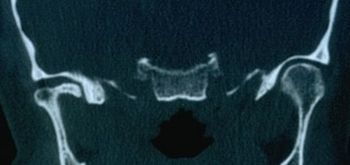
File:Atm1 sclerodermia.jpg|'''<!--85-->Figure 3:''' | File:Atm1 sclerodermia.jpg|'''<!--85-->Figure 3:''' Tomographie informatisée de l'ATM | ||
File:Spasmo emimasticatorio assiografia.jpg|'''<!--87-->Figure 4:''' | File:Spasmo emimasticatorio assiografia.jpg|'''<!--87-->Figure 4:''' Axiographie du patient montrant un aplatissement de la mastication sur le condyle droit | ||
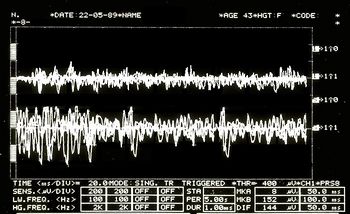
File:EMG2.jpg|'''<!--89-->Figure 5:''' | File:EMG2.jpg|'''<!--89-->Figure 5:''' Modèle interférentiel EMG. Traces supérieures superposées correspondant au masséter droit, inférieures au masséter gauche. | ||
</gallery> | </gallery> | ||
</center> | </center> | ||
Soit alors <math>P(D)</math> la probabilité de trouver, dans l'échantillon de nos <math>n</math> personnes, des individus qui présentent les éléments appartenant à l'ensemble <math>D=\{\delta_1,\delta_2,...,\delta_n\}</math> précité. | |||
Afin de tirer parti des informations fournies par ce jeu de données, le concept de partition de pertinence causale est introduit: | |||
==== | ====La partition de la pertinence causale==== | ||
: | :Soit toujours <math>n</math> le nombre de personnes sur lesquelles nous devons mener les analyses, si nous divisons (sur la base de certaines conditions comme expliqué ci-dessous) ce groupe en <math>k</math> sous-ensembles <math>C_i</math> avec <math>i=1,2,\dots,k</math>, un cluster est créé qui s'appelle un "ensemble de partition" <math>\pi</math>: | ||
:<math>\pi = \{C_1, C_2,\dots,C_k \} \qquad \qquad \text{ | :<math>\pi = \{C_1, C_2,\dots,C_k \} \qquad \qquad \text{avec} \qquad \qquad C_i \subset n , </math> | ||
où avec le symbolisme <math>C_i \subset n </math> il indique que la sous-classe <math>C_i</math> est contenue dans <math>n</math>. | |||
La partition <math>\pi</math>, pour être définie comme une partition de pertinence causale, doit avoir ces propriétés : | |||
# | #Pour chaque sous-classe <math>C_i</math> la condition doit appliquer <math>rc=P(D \mid C_i)- P(D )\neq 0, </math> c'est-à-dire la probabilité de trouver dans le sous-groupe <math>C_i</math> une personne qui présente les symptômes, les signes cliniques et les éléments appartenant à l'ensemble <math>D=\{\delta_1,\delta_2,...,\delta_n\}</math>. Une partition causalement pertinente de ce type est dite '''homogène'''. | ||
# | #Chaque sous-ensemble <math>C_i</math> doit être «élémentaire», c'est-à-dire qu'il ne doit pas être divisé en d'autres sous-ensembles, car s'ils existaient, ils n'auraient aucune pertinence causale. | ||
Supposons maintenant, par exemple, que la population échantillon <math>n</math>, à laquelle appartient notre bonne patiente Mary Poppins, soit une catégorie de sujets âgés de 20 à 70 ans. Nous supposons également que dans cette population nous avons ceux qui présentent les éléments appartenant à la ensemble de données <math>D=\{\delta_1,.....\delta_n\}</math> qui correspondent aux tests de laboratoire mentionnés ci-dessus et précis dans '[[La logique du langage classique]]'. Supposons que dans un échantillon de 10 000 sujets de 20 à 70 nous aurons une incidence de 30 sujets <math>p(D)=0.003</math> présentant des signes cliniques <math>\delta_1</math> et <math>\delta_4 | |||
</math>. Nous avons préféré utiliser ces rapports pour la démonstration du processus probabiliste car dans la littérature les données concernant les signes cliniques et les symptômes des troubles temporo-mandibulaires présentent une trop grande variation ainsi qu'une incidence trop élevée à notre avis.<ref name=":2">{{Cite book | |||
</math>. | |||
| autore = Pantoja LLQ | | autore = Pantoja LLQ | ||
| autore2 = De Toledo IP | | autore2 = De Toledo IP | ||
| Line 187: | Line 180: | ||
| PMCID = | | PMCID = | ||
| DOI = | | DOI = | ||
| oaf = <!-- qualsiasi valore --> | | oaf = <!-- qualsiasi valore --> | ||
| LCCN = | | LCCN = | ||
| Line 208: | Line 185: | ||
}}</ref> | }}</ref> | ||
Un exemple de partition avec probabilité présumée dans laquelle la dégénérescence de l'ATM (Deg.TMJ) se produit en conjonction avec des troubles temporo-mandibulaires (TMD) serait le suivant : | |||
{| | {| | ||
|+ | |+ | ||
|<math>P(D| Deg.TMJ \cap TMDs)=0.95 \qquad \qquad \; </math> | |<math>P(D| Deg.TMJ \cap TMDs)=0.95 \qquad \qquad \; </math> | ||
| | | | ||
| | |où | ||
| | | | ||
| | | | ||
| Line 220: | Line 197: | ||
|<math>P(D| Deg.TMJ \cap noTMDs)=0.3 \qquad \qquad \quad </math> | |<math>P(D| Deg.TMJ \cap noTMDs)=0.3 \qquad \qquad \quad </math> | ||
| | | | ||
| | |où | ||
| | | | ||
| | | | ||
| Line 227: | Line 204: | ||
|<math>P(D| no Deg.TMJ \cap TMDs)=0.199 \qquad \qquad \; </math> | |<math>P(D| no Deg.TMJ \cap TMDs)=0.199 \qquad \qquad \; </math> | ||
| | | | ||
| | |où | ||
| | | | ||
| | | | ||
| Line 234: | Line 211: | ||
|<math>P(D| noDeg.TMJ \cap noTMDs)=0.001 \qquad \qquad \;</math> | |<math>P(D| noDeg.TMJ \cap noTMDs)=0.001 \qquad \qquad \;</math> | ||
| | | | ||
| | |où | ||
| | | | ||
| | | | ||
|<math> C_4\equiv noDeg.TMJ \cap noTMDs</math> | |<math> C_4\equiv noDeg.TMJ \cap noTMDs</math> | ||
|} | |} | ||
{{q2|Une partition homogène fournit ce que nous avons l'habitude d'appeler le Diagnostic Différentiel|}} | |||
====Situations cliniques==== | |||
Ces probabilités conditionnelles démontrent que chacune des quatre sous-classes de la partition est causalement pertinente pour les données patient <math>D=\{\delta_1,.....\delta_n\}</math> dans l'échantillon de population <math>PO</math>. Compte tenu de la partition susmentionnée de la classe de référence, nous avons les situations cliniques suivantes : | |||
==== | *Mary Poppins <math>\in</math> dégénérescence de l'articulation temporo-mandibulaire <math>\cap</math> Troubles temporo-mandibulaires | ||
*Mary Poppins <math>\in</math> | |||
*Mary Poppins <math>\in</math> | *Mary Poppins <math>\in</math> dégénérescence de l'articulation temporo-mandibulaire <math>\cap</math> pas de troubles temporo-mandibulaires | ||
*Mary Poppins <math>\in</math> | *Mary Poppins <math>\in</math> pas de dégénérescence de l'articulation temporo-mandibulaire <math>\cap</math> Troubles temporo-mandibulaires | ||
*Mary Poppins <math>\in</math> | *Mary Poppins <math>\in</math> pas de dégénérescence de l'articulation temporo-mandibulaire <math>\cap</math> pas de troubles temporo-mandibulaires | ||
Pour arriver au diagnostic final ci-dessus, nous avons effectué une analyse probabiliste-causale de l'état de santé de Mary Poppins dont les données initiales étaient de <math>D=\{\delta_1,.....\delta_n\}</math>. | |||
En général, on peut se référer à un processus logique dans lequel on examine les éléments suivants : | |||
* | *un individu: <math>a</math> | ||
* | *son jeu de données initial<math>D=\{\delta_1,.....\delta_n\}</math> | ||
* | *un échantillon de population <math>n</math> auquel il appartient, | ||
* | *une probabilité de base <math>P(D)=0,003</math> | ||
A ce stade, nous devons introduire des arguments trop spécialisés qui éloigneraient le lecteur du sujet mais qui ont une grande importance épistémique pour lesquels nous essaierons d'extraire le fil logique le plus décrit du concept Analysandum/Analysans. | |||
L'analyse probabiliste-causale de <math>D=\{\delta_1,.....\delta_n\}</math> est alors un couple des formes logiques suivantes (Analysandum / Analysans<ref>{{Cite book | |||
| autore = Westmeyer H | | autore = Westmeyer H | ||
| titolo = The diagnostic process as a statistical-causal analysis | | titolo = The diagnostic process as a statistical-causal analysis | ||
| Line 278: | Line 254: | ||
| LCCN = | | LCCN = | ||
| OCLC = | | OCLC = | ||
}}</ref>) | }}</ref>) | ||
*'''Analysandum''' <math> = \{P(D),a\}</math>: | *'''Analysandum''' <math> = \{P(D),a\}</math>: est une forme logique qui contient deux paramètres : la probabilité <math>P(D)</math> de sélectionner une personne qui présente les symptômes et les éléments appartenant à l'ensemble <math>D=\{\delta_1,\delta_2,...,\delta_n\}</math>, et l'individu générique <math>a</math> qui est sujet à ces symptômes. | ||
*'''Analysan <math>= \{\pi,a,KB\}</math>''': | *'''Analysan <math>= \{\pi,a,KB\}</math>''':est une forme logique qui contient trois paramètres : la partition <math>\pi</math>, l'individu générique <math>a</math> appartenant à l'échantillon de population <math>n</math> et ''<math>KB</math>'' (Base de connaissances) qui comprend un ensemble d'énoncés <math>n>1</math> de probabilité conditionnée. | ||
Par exemple, on peut conclure que le diagnostic définitif est le suivant : | |||
<math>P(D| Deg.TMJ \cap TMDs)=0.95</math> - | <math>P(D| Deg.TMJ \cap TMDs)=0.95</math> - cela signifie que notre Mary Poppins est touchée à 95% par les TMD, puisqu'elle a une dégénérescence de l'articulation temporo-mandibulaire en plus des données positives <math>D=\{\delta_1,.....\delta_n\}</math> | ||
Latest revision as of 15:01, 8 March 2023
Analyse probabiliste-causale
De ces prémisses, il est clair que le diagnostic clinique est effectué en utilisant la méthode dite hypothético-déductive appelée DN[1] (deductive-nomological model[2]). Mais ce n'est pas réaliste, car les connaissances médicales utilisées dans la prise de décision clinique ne contiennent guère de lois déterministes causales pour permettre des explications causales et, par conséquent, pour formuler des diagnostics cliniques, entre autres dans le contexte spécialisé. Essayons d'analyser à nouveau le cas de notre Mary Poppins, en essayant cette fois une approche probabiliste-causale. Considérons un nombre d'individus, y compris les personnes qui signalent une douleur orofaciale qui ont généralement une dégénérescence osseuse de l'articulation temporo-mandibulaire. Cependant, il peut également y avoir d'autres causes apparemment sans rapport. Nous devons traduire mathématiquement la « pertinence » que ces incertitudes causales ont dans la détermination d'un diagnostic.
La pertinence décontractée
Pour ce faire on considère le degré de pertinence causale d'un événement par rapport à un événement où :
- = patients atteints de dégénérescence osseuse de l'articulation temporo-mandibulaire
- = patients signalant des douleurs bucco-faciales
- =patients sans dégénérescence osseuse de l'articulation temporo-mandibulaire
Nous utiliserons la probabilité conditionnelle , c'est-à-dire la probabilité que l'événement ne se produise qu'après que l'événement se soit déjà produit. Avec ces prémisses, la pertinence causale de l'échantillon de patients est :
où
- indique la probabilité que certaines personnes (parmi prises en compte) souffrent de Douleurs Orofaciales causées par la dégénérescence osseuse de l'articulation temporo-mandibulaire,
- alors que
- indique la probabilité que d'autres personnes (toujours parmi pris en considération) souffrent de Douleur Orofaciale conditionnée par autre chose qu'une dégénérescence osseuse de l'articulation temporo-mandibulaire.
- Étant donné que toutes les probabilités suggèrent que est une valeur comprise entre et , le paramètre sera un nombre compris entre et .
- Les significations que nous pouvons donner à ce nombre sont les suivantes:
- on a les cas extrêmes (qui en réalité ne se produisent jamais) qui sont :
- indiquant que la seule cause de douleur orofaciale est la dégénérescence osseuse de l'ATM,
- ce qui indique que la cause de la douleur orofaciale n'est jamais une dégénérescence osseuse de l'ATM mais autre chose,
- indiquant que la probabilité que la douleur orofaciale soit causée par une dégénérescence osseuse de l'ATM ou autrement est exactement la même,
- et les cas intermédiaires (qui sont les cas réalistes)
- indiquant que la cause de la douleur orofaciale est plus susceptible d'être une dégénérescence osseuse de l'ATM,
- ce qui indique que la cause de la douleur orofaciale n'est probablement pas la dégénérescence osseuse de l'ATM.
Deuxième approche clinique
(survolez les images)
Soit alors la probabilité de trouver, dans l'échantillon de nos personnes, des individus qui présentent les éléments appartenant à l'ensemble précité.
Afin de tirer parti des informations fournies par ce jeu de données, le concept de partition de pertinence causale est introduit:
La partition de la pertinence causale
- Soit toujours le nombre de personnes sur lesquelles nous devons mener les analyses, si nous divisons (sur la base de certaines conditions comme expliqué ci-dessous) ce groupe en sous-ensembles avec , un cluster est créé qui s'appelle un "ensemble de partition" :
où avec le symbolisme il indique que la sous-classe est contenue dans .
La partition , pour être définie comme une partition de pertinence causale, doit avoir ces propriétés :
- Pour chaque sous-classe la condition doit appliquer c'est-à-dire la probabilité de trouver dans le sous-groupe une personne qui présente les symptômes, les signes cliniques et les éléments appartenant à l'ensemble . Une partition causalement pertinente de ce type est dite homogène.
- Chaque sous-ensemble doit être «élémentaire», c'est-à-dire qu'il ne doit pas être divisé en d'autres sous-ensembles, car s'ils existaient, ils n'auraient aucune pertinence causale.
Supposons maintenant, par exemple, que la population échantillon , à laquelle appartient notre bonne patiente Mary Poppins, soit une catégorie de sujets âgés de 20 à 70 ans. Nous supposons également que dans cette population nous avons ceux qui présentent les éléments appartenant à la ensemble de données qui correspondent aux tests de laboratoire mentionnés ci-dessus et précis dans 'La logique du langage classique'. Supposons que dans un échantillon de 10 000 sujets de 20 à 70 nous aurons une incidence de 30 sujets présentant des signes cliniques et . Nous avons préféré utiliser ces rapports pour la démonstration du processus probabiliste car dans la littérature les données concernant les signes cliniques et les symptômes des troubles temporo-mandibulaires présentent une trop grande variation ainsi qu'une incidence trop élevée à notre avis.[3][4][5][6][7]
Un exemple de partition avec probabilité présumée dans laquelle la dégénérescence de l'ATM (Deg.TMJ) se produit en conjonction avec des troubles temporo-mandibulaires (TMD) serait le suivant :
| où | |||||
| où | |||||
| où | |||||
| où |
Situations cliniques
Ces probabilités conditionnelles démontrent que chacune des quatre sous-classes de la partition est causalement pertinente pour les données patient dans l'échantillon de population . Compte tenu de la partition susmentionnée de la classe de référence, nous avons les situations cliniques suivantes :
- Mary Poppins dégénérescence de l'articulation temporo-mandibulaire Troubles temporo-mandibulaires
- Mary Poppins dégénérescence de l'articulation temporo-mandibulaire pas de troubles temporo-mandibulaires
- Mary Poppins pas de dégénérescence de l'articulation temporo-mandibulaire Troubles temporo-mandibulaires
- Mary Poppins pas de dégénérescence de l'articulation temporo-mandibulaire pas de troubles temporo-mandibulaires
Pour arriver au diagnostic final ci-dessus, nous avons effectué une analyse probabiliste-causale de l'état de santé de Mary Poppins dont les données initiales étaient de .
En général, on peut se référer à un processus logique dans lequel on examine les éléments suivants :
- un individu:
- son jeu de données initial
- un échantillon de population auquel il appartient,
- une probabilité de base
A ce stade, nous devons introduire des arguments trop spécialisés qui éloigneraient le lecteur du sujet mais qui ont une grande importance épistémique pour lesquels nous essaierons d'extraire le fil logique le plus décrit du concept Analysandum/Analysans.
L'analyse probabiliste-causale de est alors un couple des formes logiques suivantes (Analysandum / Analysans[8])
- Analysandum : est une forme logique qui contient deux paramètres : la probabilité de sélectionner une personne qui présente les symptômes et les éléments appartenant à l'ensemble , et l'individu générique qui est sujet à ces symptômes.
- Analysan :est une forme logique qui contient trois paramètres : la partition , l'individu générique appartenant à l'échantillon de population et (Base de connaissances) qui comprend un ensemble d'énoncés de probabilité conditionnée.
Par exemple, on peut conclure que le diagnostic définitif est le suivant :
- cela signifie que notre Mary Poppins est touchée à 95% par les TMD, puisqu'elle a une dégénérescence de l'articulation temporo-mandibulaire en plus des données positives
- ↑ Sarkar S, «Nagel on Reduction», in Stud Hist Philos Sci, 2015».
PMID:26386529
DOI:10.1016/j.shpsa.2015.05.006 - ↑ DN model of scientific explanation, also known as Hempel's model, Hempel–Oppenheim model, Popper–Hempel model, or covering law model
- ↑ Pantoja LLQ, De Toledo IP, Pupo YM, Porporatti AL, De Luca Canto G, Zwir LF, Guerra ENS, «Prevalence of degenerative joint disease of the temporomandibular joint: a systematic review», in Clin Oral Investig, 2019».
PMID:30311063
DOI:10.1007/s00784-018-2664-y - ↑ De Toledo IP, Stefani FM, Porporatti AL, Mezzomo LA, Peres MA, Flores-Mir C, De Luca Canto G, «Prevalence of otologic signs and symptoms in adult patients with temporomandibular disorders: a systematic review and meta-analysis», in Clin Oral Investig, 2017».
PMID:27511214
DOI:10.1007/s00784-016-1926-9 - ↑ Bonotto D, Penteado CA, Namba EL, Cunali PA, Rached RN, Azevedo-Alanis LR, «Prevalence of temporomandibular disorders in rugby players», in Gen Dent».
PMID:31355769 - ↑ da Silva CG, Pachêco-Pereira C, Porporatti AL, Savi MG, Peres MA, Flores-Mir C, De Luca Canto G, «Prevalence of clinical signs of intra-articular temporomandibular disorders in children and adolescents: A systematic review and meta-analysis», in Am Dent Assoc, 2016». - PMCID:26552334
DOI:10.1016/j.adaj.2015.07.017 - ↑ Gauer RL, Semidey MJ, «Diagnosis and treatment of temporomandibular disorders», in Am Fam Physician, 2015».
PMID:25822556 - ↑ Westmeyer H, «The diagnostic process as a statistical-causal analysis», in APA, 1975».
DOI:10.1007/BF00139821
This is an Open Access resource!