Difference between revisions of "Store:AC36mediotrusivo"

Latest revision as of 19:07, 26 December 2024

Molare mediotrusivo

Osservando il moto cinematico mandibolare a livello del molare mediotrusivo, si nota il cambiamento di direzione angolare rispetto al molare laterotrusivo (

73^{\circ }

) ed all'incisivo (

85^{\circ }

). Angolo che tende ad aumentare fino a raggiungere il massimo a livello del condilo (

180^{\circ }

). L'angolo così formato è conosciuto come angolo di svincolo mediotrusivo tra la cuspide centrale e distale del primo molare.La tabella 4 mostra le distanze tra i punti del tracciato ed il punto

1M_{m}

.

Tabella 4
Tracciato mediotrusivo molare	Markers	Distanza (mm)	Direzione $X$	Direzione dinamica $Y$
Figura 8: Rappresentazione grafica dei markers rilevati dal 'Replicator' nella masticazione sul lato destro del paziente nell'area inccisale.	2	0.68	Retrusiva	Medializzazione
	3	2.19	Retrusiva	Medializzazione
	4	3.22	Retrusiva	Medializzazione
	5	5.79	Protrusiva	Medializzazione
	6	7.22	Protrusiva	Inversione
	7*	4.81	Retrusiva	Lateralizzazione
	8	1.18	Retrusiva	Lateralizzazione

Come per i precedenti, la distanza lineare tra il punto $1M_{m}$ ed il punto $7M_{m}$ è risultata essere $4.81_{mm}$ mentre l'angolo è stato calcolato come: $\theta =\arccos(0.0226)\approx 91.33^{\circ }$ Per approfondire la procedura matematica, vedi la spiegazione dettagliata qui Definizione vettori ${\vec {1M_{m}7M_{m}}}=(818.8-910.7,-855.1-(-856.2))=(-91.9,1.1)$ , ${\vec {1M_{m}R_{p}^{+}}}=(912-910.7,-741.2-(-856.2))=(1.3,115)$ . Prodotto scalare: ${\vec {1M_{m}7M_{m}}}\cdot {\vec {1M_{m}R_{p}^{+}}}=(-91.9\cdot 1.3)+(1.1\cdot 115)=-119.47+126.5=7.03$ . Norme: $|{\vec {1M_{m}7M_{m}}}|={\sqrt {(-91.9)^{2}+(1.1)^{2}}}\approx 91.92$ , $|{\vec {1M_{m}R_{p}^{+}}}|={\sqrt {(1.3)^{2}+(115)^{2}}}\approx 115.02$ . Coseno: $\cos(\theta )={\frac {7.03}{91.92\cdot 115.02}}\approx 0.000665$ . Angolo: $\theta =\arccos(0.000665)\approx 90^{\circ }$ .

@@ Line 1: / Line 1: @@
-==Molare controlaterale==
+<P>
-[[File:Controlateral molar point.jpeg|left|thumb|300x300px]]
+'''Molare mediotrusivo'''
+</P>
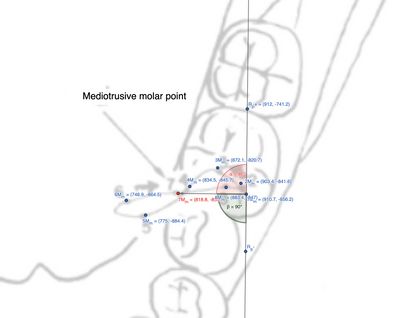
+<Div>Osservando il moto cinematico mandibolare a livello del molare mediotrusivo, si nota il cambiamento di direzione angolare rispetto al molare laterotrusivo (<math>73^\circ</math>) ed all'incisivo (<math>85^\circ</math>). Angolo che tende ad aumentare fino a raggiungere il massimo a livello del condilo            (<math>180^\circ</math>). L'angolo così formato è conosciuto come angolo di svincolo mediotrusivo tra la cuspide centrale e distale del primo molare.La tabella 4 mostra le distanze tra i punti del tracciato ed il punto <math>1M_m</math>.</Div>
+<Center>
 {| class="wikitable"
-|+Distanza dei punti in millimetri e direzioni
+! colspan="5" | Tabella 4
-!Punto!!Distanza (mm)
+|-
-!Direzione in X
+!Tracciato mediotrusivo molare
-(antero-posteriore)
+!Markers
-!Direzione in Y
+!Distanza (mm)
-(latero-mediale)
+!Direzione
+<math>X</math>
+!Direzione dinamica
+<math>Y</math>
 |-
-|2||1
+| rowspan="8" | [[File:Figura Molare Mediotrusivo.jpg|center|400x400px|Figura 4: Rappresentazione delle distanze tra i punti mediotrusivi molari]]'''Figura 8:''' <small>Rappresentazione grafica dei markers rilevati dal 'Replicator'</small> <small>nella masticazione sul lato destro del paziente nell'area inccisale.</small>
-|Avanti||Laterale
+|2
+|0.68
+|Retrusiva
+|Medializzazione
 |-
-|3||3
+|3
-|Avanti||Laterale
+|2.19
+|Retrusiva
+|Medializzazione
 |-
-|4||7
+|4
-|Avanti||Laterale
+|3.22
+|Retrusiva
+|Medializzazione
 |-
-|5||13
+|5
-|Avanti||Laterale
+|5.79
+|Protrusiva
+|Medializzazione
 |-
-|6||15
+|6
-|Indietro||Laterale
+|7.22
+|Protrusiva
+|Inversione
 |-
-|7*||8
+|7*
-|Indietro||Laterale
+|4.81
+|Retrusiva
+|Lateralizzazione
 |-
-|8||2
+|8
-|Indietro||Laterale
+|1.18
+|Retrusiva
+|Lateralizzazione
+|-
+| colspan="4" |
 |}
+</Center>
 <br />
-Come per i precedenti abbiamo tre punti nello spazio 2D che ci interessano e cioè il punto <math>
+Come per i precedenti, la distanza lineare tra il punto <math>1M_m</math> ed il punto <math>7M_m</math> è risultata essere <math>4.81_{mm}</math>  mentre l'angolo è stato calcolato come:<math>\theta = \arccos(0.0226) \approx 91.33^\circ</math> Per approfondire la procedura matematica, vedi la spiegazione dettagliata qui{{Tooltip|2=Definizione vettori <math>\vec{1M_m7M_m} = (818.8 - 910.7, -855.1 - (-856.2)) = (-91.9, 1.1)</math>,<math>\vec{1M_mR_p^+} = (912 - 910.7, -741.2 - (-856.2)) = (1.3, 115)</math>. Prodotto scalare: <math>\vec{1M_m7M_m} \cdot \vec{1M_mR_p^+} = (-91.9 \cdot 1.3) + (1.1 \cdot 115) = -119.47 + 126.5 = 7.03</math>. Norme:<math>|\vec{1M_m7M_m}| = \sqrt{(-91.9)^2 + (1.1)^2} \approx 91.92</math>, <math>|\vec{1M_mR_p^+}| = \sqrt{(1.3)^2 + (115)^2} \approx 115.02</math>. Coseno: <math>\cos(\theta) = \frac{7.03}{91.92 \cdot 115.02} \approx 0.000665</math>. Angolo: <math>\theta = \arccos(0.000665) \approx 90^\circ</math>.}}
-P1_{mm}
+</Div>
-</math> ( punto 1 del molare mediotrusivo), il <math>
+----
-P7_{mm}
-</math> ( punto 7 del molare mediotrusivo) e del punto di riferimento <math>
-R_p
-</math><br />
-*Coordinate <math>
-P1_{mm}
-</math>  <math>
-(907.1, -852.5)
-</math>
-*Coordinate <math>
-P7_{mm}
-</math>   <math>
-(817.2, -853.5)
-</math>
-*Coordinate <math>
-R_p
-</math>  <math>
-(908.8, -711.5)
-</math>
-Questi punti rappresentano tre posizioni specifiche all'interno di un sistema masticatorio che stiamo studiando, con l'obiettivo di calcolare l'angolo tra il segmento che unisce i punti <math>
-P1_{mm}
-</math> e <math>
-P7_{mm}
-</math>, e il segmento che unisce i punti <math>
-P1_{mm}
-</math>e <math>
-R_p
-</math> Questo tipo di analisi è comune nella modellazione di movimenti articolari per comprendere come si muovono i segmenti di un sistema rispetto a un punto di riferimento, come nel caso di un sistema masticatorio. Lo stesso formalismo matematico dei precedente con ovvimanete, dati diversi si definiranno i vettori{{Tooltip|2=Innanzitutto, dobbiamo calcolare i vettori che rappresentano i segmenti tra i punti:*Il vettore tra ilpunto <math>P1_{mm} </math> e il punto <math>P7_{mm} </math>:<math>\vec{AB} = P7_{mm}  - P1_{mm}  = (817.2, -853.5) - (907.1, -852.5) = (-89.9, -1.0)</math> *Il vettore tra il punto <math> P1_{mm} </math> e ilpunto <math> R_p</math>: <math>\vec{AC} = R_p - P1_{mm} = (908.8, -711.5) - (907.1, -852.5) = (1.7, 141.0)</math>}} il prodotto scalare {{Tooltip|2=Il **prodotto scalare** tra due vettori \(\vec{AB}\) e \(\vec{AC}\) è dato dalla formula: <math> \vec{AB} \cdot \vec{AC} = AB_x \cdot AC_x + AB_y \cdot AC_y </math>. Sostituendo i valori calcolati: <math>
-\vec{AB} \cdot \vec{AC} = (-89.9) \cdot (1.7) + (-1.0) \cdot (141.0) = -152.83 + (-141) = -293.83 </math>}} l calcolo della norma{{Tooltip|2=Le norme (lunghezze) dei due vettori sono calcolate con la formula della lunghezza del vettore:<math>|\vec{AB}| = \sqrt{AB_x^2 + AB_y^2} = \sqrt{(-89.9)^2 + (-1.0)^2} = \sqrt{8082.01 + 1.0} = \sqrt{8083.01} \approx 89.88</math><math>|\vec{AC}| = \sqrt{AC_x^2 + AC_y^2} = \sqrt{(1.7)^2 + (141.0)^2} = \sqrt{2.89 + 19881.0} = \sqrt{19883.89} \approx 141.02</math>}} e l'angolo {{Tooltip|2=Ora possiamo usare la formula per il coseno dell'angolo tra i due vettori:<math>\cos(\theta) = \frac{\vec{AB} \cdot \vec{AC}}{|\vec{AB}| \cdot |\vec{AC}|}</math>Sostituendo i valori:<math>\cos(\theta) = \frac{-293.83}{89.88 \cdot 141.02} = \frac{-293.83}{12676.82} \approx -0.0232</math>
-}}.
-Infine,la distanza lineare tra il punto 1 ed il punto 7* è risultata essere <math>
-.99
-</math> mm e  l'angolo <math>
-\theta
-</math>  è calcolato tramite la funzione arcoseno:
-<math>
-\theta = \arccos(-0.0232) \approx 91.33^\circ
-</math>
-==Conclusione della cinematica del molare mediotrusivo==
-L'analisi del movimento articolare del molare controlaterale, sul lato mediotrusivo, rivela informazioni importanti sulla dinamica e sull'adattamento del molare durante i movimenti masticatori laterali. Calcolando le distanze e gli angoli tra punti chiave con l'uso della trigonometria vettoriale, è possibile ottenere una rappresentazione dettagliata del comportamento biomeccanico e della stabilità del molare controlaterale in relazione al movimento mandibolare.
-Le distanze lineari tra i punti, riportate in millimetri, evidenziano una complessa sequenza di spostamenti in direzione antero-posteriore e latero-mediale. In particolare, il movimento del molare è influenzato dalla posizione e dalla traiettoria del condilo controlaterale, con transizioni tra avanzamenti e arretramenti che riflettono il percorso anatomico e le influenze muscolari che guidano il movimento.
-Dal punto di vista angolare, il calcolo dell'angolo di circa '''91.33°''' indica un movimento quasi perpendicolare rispetto ai segmenti di riferimento, suggerendo che il molare controlaterale mantiene una posizione relativamente stabile rispetto all'asse antero-posteriore durante il movimento mediotrusivo. Un angolo così vicino ai 90° può essere indicativo di un bilanciamento tra le forze che agiscono sul molare, assicurando la necessaria stabilità laterale e contribuendo alla funzione masticatoria in modo ottimale.
-Questa analisi matematica del molare controlaterale fornisce un quadro chiaro delle dinamiche masticatorie che influenzano questo punto specifico. L'applicazione del prodotto scalare e del calcolo vettoriale per determinare angoli e distanze supporta una comprensione più profonda delle interazioni articolari, essenziale per identificare eventuali disfunzioni e per guidare i trattamenti di riabilitazione. I risultati di questa analisi non solo contribuiscono alla diagnosi e alla gestione dei disturbi temporomandibolari, ma possono anche migliorare la pianificazione terapeutica nei casi in cui è richiesta una stabilizzazione o una correzione della funzione masticatoria.