|
|
| (39 intermediate revisions by the same user not shown) |
| Line 1: |
Line 1: |
| == Distanze e Direzioni ==
| | <p> |
| | '''Condilo Laterotrusivo''' |
| | </p> |
|
| |
|
| === Condilo Laterotrusivo ===
| | <Div>Questo paragrafo illustra un processo matematico per calcolare la distanza e l'angolo formato tra due segmenti in un piano 2D, con applicazione nella cinematica mandibolare. La spiegazione riguarda il calcolo degli angoli tra vettori che rappresentano movimenti articolari, ad esempio i condili durante i movimenti mandibolari (Figura 5 e Tabella 1). |
| Questo paragrafo illustra un processo matematico utilizzato per calcolare la distanza e l'angolo formato tra due segmenti in un piano 2D, con applicazione nella cinematica mandibolare. La spiegazione riguarda come determinare l'angolo tra due vettori che rappresentano movimenti articolari all'interno di un sistema articolare, ad esempio i condili durante i movimenti della mandibola. ( Figura 2 e tabella 1) | |
| | |
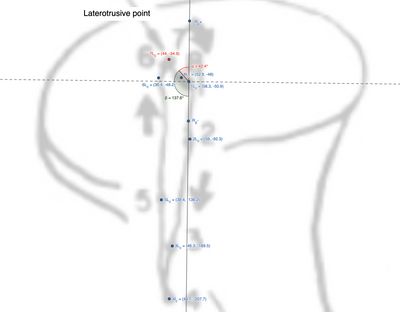
| [[File:Angolo laterotrusivo TMJ.jpg|left|thumb|'''Figura 2:''' Rappresentazione grafica reale dei punti marcati nel ciclo masticatorio]]
| |
|
| |
|
| | <Center> |
| {| class="wikitable" | | {| class="wikitable" |
| ! colspan="4" |Tabella 1 | | ! colspan="5" |Tabella 1 |
| |- | | |- |
| !Punto | | !<small>Tracciato masticatorio</small> |
| !Distanza | | !<small>Markers</small> |
| (mm) | | !<small>Distanza (mm)</small> |
| !Direzione | | !<small>Direzione</small> |
| (X - antero-posteriore)
| | <small><math>X</math></small> |
| !Direzione | | !<small>Direzione</small> <small><math>Y</math></small> |
| (Y - latero-mediale)
| | |- |
| |- | | | rowspan="9" |[[File:Figura 2 finale mod..jpg|center|400x400px|'''Figura 2:''' Rappresentazione grafica reale dei punti marcati nel ciclo masticatorio]]<small>'''Figura 5:''' Sovrapposizione dei marker in Geogebra nel tracciato cinematico del condilo laterotrusivo</small> |
| |2 | | |2 |
| |4.14 | | |1.734 |
| |Avanti | | |Protrusiva |
| |Mediale | | |Parallela |
| |- | | |- |
| |3 | | |3 |
| |11.92 | | |4.99 |
| |Avanti | | |Protrusiva |
| |Mediale | | |Lateralizzazione |
| |- | | |- |
| |4 | | |4 |
| |15.75 | | |6.59 |
| |Avanti | | |Protrusiva |
| |Mediale | | |Lateralizzazione |
| |- | | |- |
| |5 | | |5 |
| |8.76 | | |3.66 |
| |Avanti | | |Inversione |
| |Mediale | | |Inversione |
| |- | | |- |
| |6 | | |6 |
| |2.21 | | |0.923 |
| |Indietro | | |Retrusiva |
| |Laterale | | |Lateralizzazione |
| |- | | |- |
| |7* | | |7* |
| | 2.15 | | |0.898 |
| |Indietro | | |Protrsiva |
| | | |Medializzazione |
| |Laterale | |
| |- | | |- |
| |8 | | |8 |
| |0.61 | | |0.257 |
| |Indietro | | |Protrusiva |
| |Laterale | | |Medializzazione |
| | | |- |
| |- | | | colspan="4" | |
| | colspan="4" |Rappresentazione delle distanze e dell'angolo formato tra i puntimarcati nel ciclo masticatorio riferiti al punto 1 di massima intercuspidazione. IL punto 7* è il punto considerato per lo specifico calcolo del condilo laterotrusivo | | |- |
| |} | | |} |
| | | </Center> |
| Osservando la tabella la distanza tra il punto 1 e il punto 7 è correttamente circa 2.15 mm.{{Tooltip|2=Dobbiamo calcolare la distanza euclidea tra i punti <math>P_1 = (58.3, -50.9)</math> e <math>P_7 = (44, -34.9)</math>. La formula per la distanza euclidea tra due punti <math>(x_1, y_1)</math> e <math>(x_2, y_2)</math> è:<math>\text{distanza} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}</math>'''Sostituendo i valori''':<math>
| |
| \text{distanza} = \sqrt{(44 - 58.3)^2 + (-34.9 + 50.9)^2}
| |
| </math><math>\text{distanza} =\sqrt{(-14.3)^2 + (16.0)^2} = \sqrt{204.49 + 256.0} = \sqrt{460.49} \approx 21.46 \, \text{pixel}</math>A questo punto, per convertire in millimetri, moltiplichiamo la distanza in pixel per il fattore di conversione (che supponiamo essere 0.1 mm/pixel, come indicato nel modello):<math>\text{distanza in mm} = 21.46 \times 0.1 = 2.146 \, \text{mm}</math>}} # Dobbiamo calcolare la distanza euclidea tra i punti <math>P_1 = (58.3, -50.9)</math> e <math>P_7 = (44, -34.9)</math>. La formula per la distanza euclidea tra due punti <math>(x_1, y_1)</math> e <math>(x_2, y_2)</math> è:<math>\text{distanza} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}</math>'''Sostituendo i valori''':<math>
| |
| \text{distanza} = \sqrt{(44 - 58.3)^2 + (-34.9 + 50.9)^2}
| |
| </math><math>\text{distanza} =\sqrt{(-14.3)^2 + (16.0)^2} = \sqrt{204.49 + 256.0} = \sqrt{460.49} \approx 21.46 \, \text{pixel}</math>A questo punto, per convertire in millimetri, moltiplichiamo la distanza in pixel per il fattore di conversione (che supponiamo essere 0.1 mm/pixel, come indicato nel modello):<math>\text{distanza in mm} = 21.46 \times 0.1 = 2.146 \, \text{mm}</math>
| |
| | |
| | |
| '''Calcolo dell'angolo tra i punti 1, 7 e la linea tratteggiata'''
| |
| | |
| Per calcolare l'angolo tra il punto 1, il punto 7 e la linea tratteggiata che interseca il punto 1, dobbiamo utilizzare la trigonometria.
| |
| | |
| *'''Punti e coordinate coinvolte'''
| |
| **Nel contesto della nostra analisi, abbiamo tre punti nello spazio 2D che ci interessano
| |
| **Coordinate <math>P1_{L}</math> del punto 1 del condilo laterotrusivo: <math>(58.3, -50.9)</math>
| |
| **Coordinate <math>P7_{L}</math> del punto 7 del condilo laterotrusivo: <math>(44,-34.9)</math>
| |
| **Coordinate <math>R</math> del punto di riferimento del condilo laterotrusivo: <math>(60.7, 158.7)</math>
| |
| | |
| | |
| Questi punti rappresentano tre posizioni specifiche all'interno di un sistema articolare che stiamo studiando, con l'obiettivo di calcolare l'angolo tra il segmento che unisce i punti <math>P1_{L}</math> e <math>P7_{L}</math>, e il segmento che unisce i punti <math>P1_{L}</math> e <math>R</math>. Questo tipo di analisi è comune nella modellazione di movimenti articolari per comprendere come si muovono i segmenti di un sistema rispetto a un punto di riferimento, come nel caso di un sistema masticatorio.
| |
| | |
| '''Iter matematico per il calcolo dell'angolo'''
| |
| | |
| L'angolo tra due segmenti può essere calcolato utilizzando la **trigonometria vettoriale** e, in particolare, il **prodotto scalare**. Questo metodo è utile quando vogliamo determinare la relazione angolare tra due movimenti distinti nello spazio.
| |
| | |
| '''1. Definizione dei vettori'''
| |
| | |
| Innanzitutto, dobbiamo calcolare i vettori che rappresentano i segmenti tra i punti:
| |
| | |
| *Il vettore tra il punto 1<sub>L</sub> e il punto 7<sub>L</sub>:
| |
| | |
| <math>
| |
| \vec{AB} = P7_{L} - P1_{L} = (44, -34.9) - (58.3, -50.9) = (-14.3, 16.0)
| |
| </math>
| |
| | |
| *Il vettore tra il punto 1<sub>L</sub> e il punto H₃:
| |
| | |
| <math>
| |
| \vec{AC} = R
| |
| - P1_{L} = (60.7, 158.7) - (58.3, -50.9) = (2.4, 209.6) | |
| </math>
| |
| | |
| '''2. Prodotto scalare'''
| |
| | |
| Il **prodotto scalare** tra due vettori <math>\vec{AB}</math> e <math>\vec{AC}</math> è dato dalla formula:
| |
| | |
| <math>
| |
| \vec{AB} \cdot \vec{AC} = AB_x\cdot AC_x + AB_y\cdot AC_y
| |
| </math>
| |
| | |
| Sostituendo i valori calcolati:
| |
| | |
| <math>
| |
| \vec{AB} \cdot \vec{AC} = (-14.3) \cdot (2.4) + (16.0) \cdot (209.6) = -34.32 + 3353.6 = 3319.28
| |
| </math>
| |
| | |
| '''3. Calcolo delle norme'''
| |
| | |
| Le norme (lunghezze) dei due vettori sono calcolate con la formula della lunghezza del vettore:
| |
| | |
| <math>
| |
| |\vec{AB}| = \sqrt{AB_x^2 + AB_y^2} =\sqrt{(-14.3)^2 + (16.0)^2} = \sqrt{204.49 + 256.0} = \sqrt{460.49} \approx 21.46 | |
| </math>
| |
| | |
| <math>
| |
| |\vec{AC}| = \sqrt{AC_x^2 + AC_y^2} = \sqrt{(2.4)^2 + (209.6)^2} = \sqrt{5.76 + 43944.16} = \sqrt{43949.92} \approx 209.68
| |
| </math> | |
| | |
| '''4. Calcolo dell'angolo'''
| |
| | |
| Ora possiamo usare la formula per il coseno dell'angolo tra i due vettori:
| |
| | |
| <math>
| |
| \cos(\theta) = \frac{\vec{AB} \cdot \vec{AC}}{|\vec{AB}| \cdot |\vec{AC}|}
| |
| </math>
| |
| | |
| Sostituendo i valori:
| |
| | |
| <math>
| |
| \cos(\theta) = \frac{3319.28}{21.46 \cdot 209.68} = \frac{3319.28}{4498.77} \approx 0.738
| |
| </math>
| |
| | |
| Infine, l'angolo <math>\theta</math> è calcolato tramite la funzione arcoseno:
| |
| | |
| <math>
| |
| \theta = \arccos(0.738) \approx 42.44^\circ
| |
| </math>
| |
| | |
| Con lo stesso procedimento calcoliamo le distanze e l'angolo per il molare laterotrusivo, l'incisivo, il molare mediotrusivo ed il condilo mediotrusivo per verificarne l'andamento spaziale.
| |
| | |
| ----
| |
| ==Iter Matematico per il Calcolo dell'Angolo==
| |
| | |
| L'angolo tra due vettori può essere calcolato utilizzando la **trigonometria vettoriale**. Esistono metodi diversi in base al contesto. Se i vettori sono nel piano 2D, possiamo utilizzare direttamente la funzione <math>\text{atan2}</math>. Tuttavia, in uno spazio tridimensionale, utilizziamo il **prodotto scalare** per determinare l'angolo tra i vettori.
| |
| | |
| ---
| |
| | |
| ===Calcolo nel Piano 2D con <math>\text{atan2}</math>===
| |
| | |
| Nel caso specifico dei vettori nel piano trasversale <math>(X, Y)</math>, possiamo calcolare l'angolo tra i due vettori con la formula:
| |
| | |
| <math>
| |
| \theta = \text{atan2}(\Delta y, \Delta x)
| |
| </math>
| |
| | |
| Esempio 2D:
| |
| | |
| 1. **Definizione dei vettori**:
| |
| | |
| - Il vettore tra il punto <math>1L</math> e il punto <math>7L</math>:
| |
| | |
| <math>
| |
| \vec{AB} = (X_{7L} - X_{1L}, Y_{7L} - Y_{1L}) = (44 - 58.3, -34.9 - (-50.9)) = (-14.3, 16.0)
| |
| </math>
| |
| | |
|
| |
|
| Il vettore tra il punto <math>1L</math> e il punto <math>H_3</math>:
| | Osservando la figura e la tabella, possiamo estrapolare le distanze tra i punti marcati ed in particolare segnaliamo che è stato considerato il punto <math>7L_c</math> come punto estremo in cui il condilo inverte il moto ed inizia un percorso mediali verso la massima intercuspidazione. Questo punto, anzi, la distanza tra questo punto ed il punto <math>1L_c</math> rappresenta il movimento di Bennett. Ad esempio, questa distanza è stata correttamente calcolata come circa <math>0.898 \, _\text{mm}</math> con una direzione calcolata come: |
|
| |
|
| <math> | | <math>\theta = 131.87^\circ </math> ed il corrispettivo <math>\theta^' = 42^\circ </math> |
| \vec{AC} = (X_{H3} - X_{1L}, Y_{H3} - Y_{1L}) = (60.7 - 58.3, 158.7 - (-50.9)) = (2.4, 209.6)
| |
| </math>
| |
| | |
| | |
| 2. **Calcolo dell'angolo con <math>\text{atan2}</math>**:
| |
| | |
| - Per il vettore <math>\vec{AB}</math>:
| |
| | |
| <math>
| |
| \text{Angolo di } \vec{AB} = \text{atan2}(16.0, -14.3) \approx 132^\circ
| |
| </math>
| |
| | |
| - Per il vettore <math>\vec{AC}</math>:
| |
| | |
| <math> | |
| \text{Angolo di } \vec{AC} = \text{atan2}(209.6, 2.4) \approx 89^\circ
| |
| </math>
| |
| | |
| - L'angolo tra i vettori:
| |
| | |
| <math>
| |
| \theta = |\text{Angolo di } \vec{AB} - \text{Angolo di } \vec{AC}| \approx |132^\circ - 89^\circ| = 43^\circ
| |
| </math>
| |
| | |
| ---
| |
| | |
| ===Calcolo nello Spazio 3D con Prodotto Scalare===
| |
| | |
| Se i vettori sono nello spazio tridimensionale, utilizziamo il **prodotto scalare** per determinare l'angolo tra di essi. Il prodotto scalare è definito come:
| |
| | |
| 1. **Definizione dei vettori**:
| |
| | |
| - Supponiamo che:
| |
| | |
| <math>
| |
| \vec{AB} = (-14.3, 16.0, 0.0) \quad \text{e} \quad \vec{AC} = (2.4, 209.6, 0.0)
| |
| </math>
| |
| | |
| | |
| 2. **Calcolo del prodotto scalare**:
| |
| | |
| <math>
| |
| \vec{AB} \cdot \vec{AC} = (-14.3 \cdot 2.4) + (16.0 \cdot 209.6) + (0.0 \cdot 0.0)
| |
| </math>
| |
| | |
| <math>
| |
| \vec{AB} \cdot \vec{AC} = -34.32 + 3353.6 = 3319.28
| |
| </math>
| |
| | |
| | |
| 3. **Calcolo delle norme**:
| |
| | |
| <math>
| |
| |\vec{AB}| = \sqrt{(-14.3)^2 + (16.0)^2} = \sqrt{204.49 + 256.0} = \sqrt{460.49} \approx 21.46
| |
| </math> <math>
| |
| |\vec{AC}| = \sqrt{(2.4)^2 + (209.6)^2} = \sqrt{5.76 + 43944.16} = \sqrt{43949.92} \approx 209.68
| |
| </math>
| |
| | |
| | |
| 4. **Calcolo del coseno dell'angolo**:
| |
| | |
| <math>
| |
| \cos(\theta) = \frac{\vec{AB} \cdot \vec{AC}}{|\vec{AB}| \cdot |\vec{AC}|} = \frac{3319.28}{21.46 \cdot 209.68} = \frac{3319.28}{4498.77} \approx 0.738
| |
| </math>
| |
| | |
| | |
| 5. **Determinazione dell'angolo**:
| |
| | |
| <math>
| |
| \theta = \arccos(0.738) \approx 42.44^\circ
| |
| </math>
| |
|
| |
|
| | Per chi desidera approfondire il formalismo matematico, riportiamo il calcolo dettagliato nel popup interattivo.{{Tooltip|2=Calcolo dettagliato: distanza tra <math>P_1 = (58.3, -50.9)</math> e <math>P_7 = (44, -34.9)</math>, distanza euclidea <math>\sqrt{(-14.3)^2 + (16)^2} \approx 21.47 \, \text{pixel}</math>, convertita in mm come <math>21.47 \times 0.04184 \approx 0.898 \, \text{mm}</math>, angolo <math>\theta = \arccos(-0.6665) \approx 131.87^\circ</math>.}} |
| | </Div> |
|
| |
|
| ---- | | ---- |
|
| |
| ==Conclusione==
| |
|
| |
| Per vettori bidimensionali, l'approccio più diretto è l'uso della funzione <math>\text{atan2}</math>, che semplifica il calcolo evitando la necessità di calcolare prodotti scalari e norme. Tuttavia, per il calcolo nello spazio tridimensionale, il metodo basato sul prodotto scalare rimane essenziale. Adottare il metodo corretto per il contesto specifico garantisce maggiore efficienza e precisione nei calcoli.
| |
|
| |
| ----
| |
| '''Conclusione sul Condilo Laterotrusivo'''
| |
|
| |
| L'analisi cinematica del condilo laterotrusivo evidenzia come il suo traiettorie articolare sia il risultato di una complessa combinazione di movimenti rotatori e traslatori, orientati non solo in direzione laterale ma anche in direzione retrusiva. Questo comportamento tridimensionale, che si discosta da una pura rotazione, si manifesta attraverso una traiettoria che comprende componenti antero-posteriore e latero-mediale, influenzate dall'interazione con il condilo mediotrusivo. Il movimento laterotrusivo del condilo lavorante è fondamentale per l’equilibrio funzionale mandibolare, poiché determina la traiettoria e la stabilità dei contatti occlusali durante il ciclo masticatorio.
| |
|
| |
| Attraverso l’applicazione del calcolo vettoriale, in particolare il prodotto scalare e il calcolo degli angoli tra vettori, siamo riusciti a quantificare l’orientamento e la distanza relativa tra i punti articolari chiave del condilo laterotrusivo, rappresentati nella Tabella 1 e Figura 2. Il calcolo dell’angolo tra i vettori del movimento articolare permette di comprendere come la traiettoria segua un percorso specifico di adattamento, probabilmente influenzato da microvariazioni nella morfologia articolare e dall’interazione con i tessuti circostanti. Questo schema articolare riflette le caratteristiche fisiologiche del movimento mandibolare, rendendo evidente come il condilo laterotrusivo si adatti alle richieste funzionali durante le fasi dinamiche della masticazione.
| |
|
| |
| Da un punto di vista clinico, la comprensione approfondita della cinematica condilare laterotrusiva offre un potenziale diagnostico significativo per la valutazione delle disfunzioni temporomandibolari (TMD) e delle asimmetrie mandibolari. La capacità di modellare e interpretare con precisione le variazioni angolari e spaziali del condilo laterotrusivo consente di identificare eventuali irregolarità nel pattern di movimento mandibolare, che possono essere indicative di tensioni muscolari anomale o patologie articolari. Inoltre, l’analisi quantitativa dei movimenti condilari può supportare la pianificazione di terapie ortodontiche e di dispositivi intraorali che mirino a riequilibrare le forze articolari, contribuendo a ridurre il rischio di sovraccarico e usura dei tessuti articolari.
| |
|
| |
| In sintesi, la valutazione cinematica del condilo laterotrusivo fornisce informazioni critiche non solo per il miglioramento della comprensione biomeccanica dell’articolazione temporomandibolare, ma anche per lo sviluppo di approcci terapeutici più mirati. L'integrazione di dati cinematografici e di calcoli angolari e distanze permette di costruire un quadro diagnostico e terapeutico più completo e personalizzato, offrendo al paziente una maggiore precisione nelle strategie di trattamento delle disfunzioni temporomandibolari.
| |
![]() Calcolo dettagliato: distanza tra e , distanza euclidea , convertita in mm come , angolo .
Calcolo dettagliato: distanza tra e , distanza euclidea , convertita in mm come , angolo .