Difference between revisions of "Store:MTcondilo"
| (44 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
<P>'''Condilo Mediotrusivo'''</P> | |||
< | Questi punti rappresentano posizioni specifiche all'interno di un sistema articolare che stiamo studiando, con l'obiettivo di calcolare l'angolo tra il segmento che unisce i punti <math>1M_c</math> e <math>/M_c</math>, e il segmento che unisce i punti <math>1M_c</math> e <math>R_pc</math>. Questo tipo di analisi è comune nella modellazione di movimenti articolari per comprendere come si muovono i segmenti di un sistema rispetto a un punto di riferimento, come nel caso di un sistema masticatorio. | ||
<Center> | |||
{| class="wikitable" | {| class="wikitable" | ||
! colspan="5" |Tabella 5 | |||
|- | |||
!Tracciato masticatorio | |||
!Markers | |||
!Distanza | |||
(mm) | |||
!Direzione | |||
<math>X</math> | |||
!Direzione | |||
<math>Y</math> | |||
|- | |- | ||
| rowspan="8" |[[File:Figura 5. finale.jpg|center|400x400px]]'''Figura 9:''' <small>Rappresentazione grafica dei markers rilevati dal 'Replicator'</small><small>nella masticazione sul lato destro del paziente nell'area inccisale.</small> | |||
|2||2.13||Protrusiva||Medializzazione | |||
|- | |- | ||
| | |3||6.19||Protrusiva||Medializzazione | ||
|- | |- | ||
| | |4||10.70||Protrusiva||Medializzazione | ||
|- | |- | ||
| | |5||11.09||Protrusiva||Inversione | ||
|- | |- | ||
| | |6||6.09||Protrusiva||Lateralizzazione | ||
|- | |- | ||
| | |7*||2.61||Protrusiva||Lateralizzazione | ||
|- | |- | ||
| | |8||0.50||Protrusiva||Lateralizzazione | ||
|- | |- | ||
| | | colspan="4" | | ||
|} | |} | ||
</Center> | |||
Per quanto riguarda le distanze e la direzione del punto 7 nel condilo mediotrusivo, abbiamo una distanza dal punto di partenza di <math>6.88</math>mm ed un angolo calcolato sull'arcoseno <math>\theta = \arccos(-0.971) \approx 166^\circ</math>. Infine, sottraendo questo angolo da 180°, otteniamo un angolo di <math>14^\circ</math>, noto come '''Angolo di Bennett'''. Per approfondire la procedura matematica, vedi {{Tooltip|2=Calcolo sintetico: vettore <math>\vec{AB} = (-15.9, -60.4)</math>, vettore<math>\vec{AC} = (0.2, 52.5)</math>, prodotto scalare <math>\vec{AB} \cdot \vec{AC} = -3172.62</math>, norme <math>|\vec{AB}| = 62.93</math>, <math>|\vec{AC}| = 52.50</math>, <math>\cos(\theta) = \frac{-3172.62}{62.93 \cdot 52.50} \approx-0.971</math>, <math>\theta =\arccos(-0.971) \approx 166^\circ</math>.}} | |||
</math> | |||
( | |||
</math> | |||
</math> | |||
<math> | |||
\vec{AB} | |||
</math> | |||
<math> | |||
\vec{AC} | |||
= ( | |||
</math> | |||
<math> | |||
\vec{AB} | |||
</math> | |||
<math> | |||
\ | |||
</math> | |||
---- | |||
===Discussione sulla rototraslazione condilari=== | |||
Il moto rototraslazionale dei condili è fondamentale per comprendere la cinematica mandibolare e i tracciati descritti dai denti durante la masticazione. Se i condili ruotassero semplicemente attorno a un punto fisso, i tracciati dei molari e degli incisivi sarebbero archi di cerchio con un unico centro. Tuttavia, i movimenti reali dei condili sono molto più complessi. | |||
Durante la laterotrusione, il condilo ipsilaterale (dello stesso lato) esegue un movimento che combina rotazione attorno all'asse verticale e traslazione laterale. Allo stesso tempo, il condilo controlaterale si muove principalmente in direzione mediale e anteriore, descrivendo un percorso noto come "Tragitto orbitante". | |||
'''Descrizione matematica''' | |||
Matematicamente, possiamo descrivere il moto rototraslazionale del condilo laterotrusivo come una combinazione di una rotazione attorno all'asse verticale passante per il condilo stesso e una traslazione laterale lungo una traiettoria specifica. La posizione del molare ipsilaterale in un determinato istante può essere ottenuta applicando la rotazione attorno all'asse verticale e poi la traslazione corrispondente: | |||
<math> | <math> | ||
\cos(\theta) | x_m = x_{m0} \cos(\theta) - y_{m0} \sin(\theta) + T_x | ||
</math> | </math> | ||
<math> | <math> | ||
y_m = x_{m0} \sin(\theta) + y_{m0} \cos(\theta) | |||
</math> | </math> | ||
Dove: | |||
*<math>(x_{m0}, y_{m0})</math> è la posizione iniziale del molare ipsilaterale. | |||
*<math>T_x</math> rappresenta la traslazione laterale lungo l'asse <math>x</math>. | |||
*<math>(x_m, y_m)</math> rappresenta la posizione finale del molare ipsilaterale. | |||
Man mano che il condilo ruota e si sposta lateralmente, le coordinate <math>(x_m, y_m)</math> del molare descrivono una traiettoria ellittica proiettata su un piano bidimensionale. Questo fenomeno ellittico si verifica perché il centro di rotazione istantaneo del condilo laterotrusivo non è fisso, ma si sposta continuamente a causa della traslazione laterale. Pertanto, il tracciato descritto dal molare ipsilaterale non può essere un semplice arco di cerchio, ma assume una forma ellittica. | |||
Un comportamento simile si osserva anche per il condilo controlaterale (mediotrusivo) e per gli incisivi. Sebbene il movimento del condilo mediotrusivo sia principalmente una traslazione mediale e anteriore, può essere coinvolta anche una certa '''rotazione attorno all'asse verticale'''. Questa combinazione di traslazione e rotazione porta nuovamente a tracciati ellittici per il molare controlaterale e per gli incisivi. | |||
È importante sottolineare che i tracciati ellittici osservati non sono ellissi perfette, ma curve più complesse, poiché i movimenti dei condili non sono semplici rotazioni e traslazioni costanti. Infatti, i condili seguono traiettorie più elaborate, con accelerazioni e decelerazioni, che si riflettono nella forma dei tracciati dei denti. | |||
< | Inoltre, i tracciati dei molari e degli incisivi non sono indipendenti, ma sono strettamente correlati ai movimenti dei condili corrispondenti. Pertanto, l'analisi dei tracciati dei denti può fornire informazioni preziose sulla cinematica mandibolare e sui movimenti articolari dei condili.[[File:Conica.jpg|300x300px|'''Figura 10a:''' <small>Rappresentazione generica di conica, segue descrizione dettagliata.</small>|thumb]]In conclusione, la combinazione di rotazione e traslazione dei condili durante i movimenti mandibolari impedisce ai tracciati dei molari e degli incisivi di essere semplici archi di cerchio. Invece, questi tracciati assumono forme ellittiche, poiché il centro di rotazione istantaneo dei condili si sposta continuamente a causa del moto rototraslazionale complesso. Per comprendere meglio la complessità delle traiettorie, è stato costruito un modello matematico basato su una conica passante per cinque punti strategicamente scelti, come illustrato nella figura 10a e approfondito nel prossimo paragrafo. | ||
Latest revision as of 17:59, 26 December 2024
Condilo Mediotrusivo
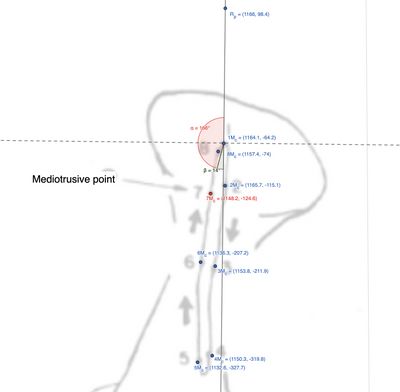
Questi punti rappresentano posizioni specifiche all'interno di un sistema articolare che stiamo studiando, con l'obiettivo di calcolare l'angolo tra il segmento che unisce i punti e , e il segmento che unisce i punti e . Questo tipo di analisi è comune nella modellazione di movimenti articolari per comprendere come si muovono i segmenti di un sistema rispetto a un punto di riferimento, come nel caso di un sistema masticatorio.
| Tabella 5 | ||||
|---|---|---|---|---|
| Tracciato masticatorio | Markers | Distanza
(mm) |
Direzione
|
Direzione
|
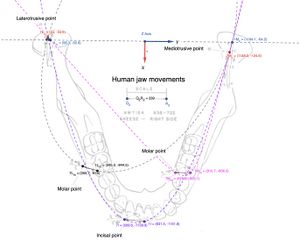
| Figura 9: Rappresentazione grafica dei markers rilevati dal 'Replicator'nella masticazione sul lato destro del paziente nell'area inccisale. | 2 | 2.13 | Protrusiva | Medializzazione |
| 3 | 6.19 | Protrusiva | Medializzazione | |
| 4 | 10.70 | Protrusiva | Medializzazione | |
| 5 | 11.09 | Protrusiva | Inversione | |
| 6 | 6.09 | Protrusiva | Lateralizzazione | |
| 7* | 2.61 | Protrusiva | Lateralizzazione | |
| 8 | 0.50 | Protrusiva | Lateralizzazione | |
Per quanto riguarda le distanze e la direzione del punto 7 nel condilo mediotrusivo, abbiamo una distanza dal punto di partenza di mm ed un angolo calcolato sull'arcoseno . Infine, sottraendo questo angolo da 180°, otteniamo un angolo di , noto come Angolo di Bennett. Per approfondire la procedura matematica, vedi ![]() Calcolo sintetico: vettore , vettore, prodotto scalare , norme , , , .
Calcolo sintetico: vettore , vettore, prodotto scalare , norme , , , .
Discussione sulla rototraslazione condilari
Il moto rototraslazionale dei condili è fondamentale per comprendere la cinematica mandibolare e i tracciati descritti dai denti durante la masticazione. Se i condili ruotassero semplicemente attorno a un punto fisso, i tracciati dei molari e degli incisivi sarebbero archi di cerchio con un unico centro. Tuttavia, i movimenti reali dei condili sono molto più complessi.
Durante la laterotrusione, il condilo ipsilaterale (dello stesso lato) esegue un movimento che combina rotazione attorno all'asse verticale e traslazione laterale. Allo stesso tempo, il condilo controlaterale si muove principalmente in direzione mediale e anteriore, descrivendo un percorso noto come "Tragitto orbitante".
Descrizione matematica
Matematicamente, possiamo descrivere il moto rototraslazionale del condilo laterotrusivo come una combinazione di una rotazione attorno all'asse verticale passante per il condilo stesso e una traslazione laterale lungo una traiettoria specifica. La posizione del molare ipsilaterale in un determinato istante può essere ottenuta applicando la rotazione attorno all'asse verticale e poi la traslazione corrispondente:
Dove:
- è la posizione iniziale del molare ipsilaterale.
- rappresenta la traslazione laterale lungo l'asse .
- rappresenta la posizione finale del molare ipsilaterale.
Man mano che il condilo ruota e si sposta lateralmente, le coordinate del molare descrivono una traiettoria ellittica proiettata su un piano bidimensionale. Questo fenomeno ellittico si verifica perché il centro di rotazione istantaneo del condilo laterotrusivo non è fisso, ma si sposta continuamente a causa della traslazione laterale. Pertanto, il tracciato descritto dal molare ipsilaterale non può essere un semplice arco di cerchio, ma assume una forma ellittica.
Un comportamento simile si osserva anche per il condilo controlaterale (mediotrusivo) e per gli incisivi. Sebbene il movimento del condilo mediotrusivo sia principalmente una traslazione mediale e anteriore, può essere coinvolta anche una certa rotazione attorno all'asse verticale. Questa combinazione di traslazione e rotazione porta nuovamente a tracciati ellittici per il molare controlaterale e per gli incisivi.
È importante sottolineare che i tracciati ellittici osservati non sono ellissi perfette, ma curve più complesse, poiché i movimenti dei condili non sono semplici rotazioni e traslazioni costanti. Infatti, i condili seguono traiettorie più elaborate, con accelerazioni e decelerazioni, che si riflettono nella forma dei tracciati dei denti.
Inoltre, i tracciati dei molari e degli incisivi non sono indipendenti, ma sono strettamente correlati ai movimenti dei condili corrispondenti. Pertanto, l'analisi dei tracciati dei denti può fornire informazioni preziose sulla cinematica mandibolare e sui movimenti articolari dei condili.
In conclusione, la combinazione di rotazione e traslazione dei condili durante i movimenti mandibolari impedisce ai tracciati dei molari e degli incisivi di essere semplici archi di cerchio. Invece, questi tracciati assumono forme ellittiche, poiché il centro di rotazione istantaneo dei condili si sposta continuamente a causa del moto rototraslazionale complesso. Per comprendere meglio la complessità delle traiettorie, è stato costruito un modello matematico basato su una conica passante per cinque punti strategicamente scelti, come illustrato nella figura 10a e approfondito nel prossimo paragrafo.