|
|
| (35 intermediate revisions by the same user not shown) |
| Line 1: |
Line 1: |
| ==Molare controlaterale==
| | <P> |
| [[File:Controlateral molar point.jpeg|left|thumb|300x300px]]
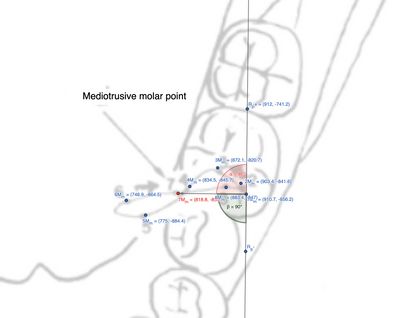
| | '''Molare mediotrusivo''' |
| | </P> |
| | |
| | <Div>Osservando il moto cinematico mandibolare a livello del molare mediotrusivo, si nota il cambiamento di direzione angolare rispetto al molare laterotrusivo (<math>73^\circ</math>) ed all'incisivo (<math>85^\circ</math>). Angolo che tende ad aumentare fino a raggiungere il massimo a livello del condilo (<math>180^\circ</math>). L'angolo così formato è conosciuto come angolo di svincolo mediotrusivo tra la cuspide centrale e distale del primo molare.La tabella 4 mostra le distanze tra i punti del tracciato ed il punto <math>1M_m</math>.</Div> |
| | |
| | <Center> |
| {| class="wikitable" | | {| class="wikitable" |
| |+Distanza dei punti in millimetri e direzioni | | ! colspan="5" | Tabella 4 |
| !Punto!!Distanza (mm) | | |- |
| !Direzione in X | | !Tracciato mediotrusivo molare |
| (antero-posteriore)
| | !Markers |
| !Direzione in Y | | !Distanza (mm) |
| (latero-mediale)
| | !Direzione |
| | <math>X</math> |
| | !Direzione dinamica |
| | <math>Y</math> |
| | |- |
| | | rowspan="8" | [[File:Figura Molare Mediotrusivo.jpg|center|400x400px|Figura 4: Rappresentazione delle distanze tra i punti mediotrusivi molari]]'''Figura 8:''' <small>Rappresentazione grafica dei markers rilevati dal 'Replicator'</small> <small>nella masticazione sul lato destro del paziente nell'area inccisale.</small> |
| | |2 |
| | |0.68 |
| | |Retrusiva |
| | |Medializzazione |
| |- | | |- |
| |2||1.11 | | |3 |
| |Avanti||Laterale | | |2.19 |
| | |Retrusiva |
| | |Medializzazione |
| |- | | |- |
| |3||3.89 | | |4 |
| |Avanti||Laterale | | |3.22 |
| | |Retrusiva |
| | |Medializzazione |
| |- | | |- |
| |4||7.76 | | |5 |
| |Avanti||Laterale | | |5.79 |
| | |Protrusiva |
| | |Medializzazione |
| |- | | |- |
| |5||13.75 | | |6 |
| |Avanti||Laterale | | |7.22 |
| | |Protrusiva |
| | |Inversione |
| |- | | |- |
| |6||15.71 | | |7* |
| |Indietro||Laterale | | |4.81 |
| | |Retrusiva |
| | |Lateralizzazione |
| |- | | |- |
| |7||8.99 | | |8 |
| |Indietro||Laterale | | |1.18 |
| | |Retrusiva |
| | |Lateralizzazione |
| |- | | |- |
| |8||2.43 | | | colspan="4" | |
| |Indietro||Laterale
| |
| |} | | |} |
| | </Center> |
|
| |
|
| <br /> | | <br /> |
| ===Descrizione focalizzata dell'analisi matematica dei punti===
| |
|
| |
| ====Punti e coordinate coinvolte====
| |
|
| |
| Nel contesto della nostra analisi, abbiamo tre punti nello spazio 2D che ci interessano:
| |
|
| |
| <br />
| |
|
| |
| *Coordinate <math>
| |
| P1m_{cl}
| |
| </math> del punto 1 dell'incisivo sul lato lavorante: <math>
| |
| (907.1, -852.5)
| |
| </math>
| |
| *Coordinate <math>
| |
| P7 m_{cl}
| |
| </math> del punto 7 dell'incisivo sul lato lavorante: <math>
| |
| (817.2, -853.5)
| |
| </math>
| |
| *Coordinate <math>
| |
| H3m_{cl}
| |
| </math> del punto di riferimento dell'incisivo sul lato lavorante: <math>
| |
|
| |
| (908.8, -711.5)
| |
| </math>
| |
|
| |
| <br />
| |
|
| |
| *
| |
|
| |
| Questi punti rappresentano tre posizioni specifiche all'interno di un sistema articolare che stiamo studiando, con l'obiettivo di calcolare l'angolo tra il segmento che unisce i punti <math>
| |
| P1m_{cl}
| |
| </math> e <math>
| |
| P7 m_{cl}
| |
| </math>, e il segmento che unisce i punti <math>
| |
| P1m_{cl}
| |
| </math>e <math>
| |
| H3m_{cl}
| |
| </math> Questo tipo di analisi è comune nella modellazione di movimenti articolari per comprendere come si muovono i segmenti di un sistema rispetto a un punto di riferimento, come nel caso di un sistema masticatorio.
| |
|
| |
| ====Iter matematico per il calcolo dell'angolo====
| |
|
| |
| L'angolo tra due segmenti può essere calcolato utilizzando la **trigonometria vettoriale** e, in particolare, il **prodotto scalare**. Questo metodo è utile quando vogliamo determinare la relazione angolare tra due movimenti distinti nello spazio.
| |
|
| |
| ====1. Definizione dei vettori====
| |
|
| |
| Innanzitutto, dobbiamo calcolare i vettori che rappresentano i segmenti tra i punti:
| |
|
| |
| *Il vettore tra il punto <math>
| |
| P1m_{cl}
| |
| </math> e il punto <math>
| |
| P7 m_{cl}
| |
| </math>:
| |
|
| |
| <math>
| |
| \vec{AB} = P7 m_{cl} - P1m_{cl} = (817.2, -853.5) - (907.1, -852.5) = (-89.9, -1.0)
| |
| </math>
| |
|
| |
| *Il vettore tra il punto <math>
| |
| P1m_{cl}
| |
| </math>e il punto <math>
| |
| H3m_{cl}
| |
| </math>:
| |
|
| |
| <math>
| |
| \vec{AC} = H3m_{cl} - P1m_{cl} = (908.8, -711.5) - (907.1, -852.5) = (1.7, 141.0)
| |
| </math>
| |
|
| |
| ====2. Prodotto scalare====
| |
|
| |
| Il **prodotto scalare** tra due vettori \(\vec{AB}\) e \(\vec{AC}\) è dato dalla formula:
| |
|
| |
| <math>
| |
| \vec{AB} \cdot \vec{AC} = AB_x \cdot AC_x + AB_y \cdot AC_y
| |
| </math>
| |
|
| |
| Sostituendo i valori calcolati:
| |
|
| |
| <math>
| |
| \vec{AB} \cdot \vec{AC} = (-89.9) \cdot (1.7) + (-1.0) \cdot (141.0) = -152.83 + (-141) = -293.83
| |
| </math>
| |
|
| |
| ====3. Calcolo delle norme====
| |
|
| |
| Le norme (lunghezze) dei due vettori sono calcolate con la formula della lunghezza del vettore:
| |
|
| |
| <math>
| |
| |\vec{AB}| = \sqrt{AB_x^2 + AB_y^2} = \sqrt{(-89.9)^2 + (-1.0)^2} = \sqrt{8082.01 + 1.0} = \sqrt{8083.01} \approx 89.88
| |
| </math>
| |
|
| |
| <math>
| |
| |\vec{AC}| = \sqrt{AC_x^2 + AC_y^2} = \sqrt{(1.7)^2 + (141.0)^2} = \sqrt{2.89 + 19881.0} = \sqrt{19883.89} \approx 141.02
| |
| </math>
| |
|
| |
| ====4. Calcolo dell'angolo====
| |
|
| |
| Ora possiamo usare la formula per il coseno dell'angolo tra i due vettori:
| |
|
| |
| <math>
| |
| \cos(\theta) = \frac{\vec{AB} \cdot \vec{AC}}{|\vec{AB}| \cdot |\vec{AC}|}
| |
| </math>
| |
|
| |
| Sostituendo i valori:
| |
|
| |
| <math>
| |
| \cos(\theta) = \frac{-293.83}{89.88 \cdot 141.02} = \frac{-293.83}{12665.58} \approx -0.0232
| |
| </math>
| |
|
| |
| Infine, l'angolo \(\theta\) è calcolato tramite la funzione arcoseno:
| |
|
| |
| <math>
| |
| \theta = \arccos(-0.0232) \approx 91.33^\circ
| |
| </math>
| |
|
| |
| ====Motivo dell'analisi====
| |
|
| |
| L'obiettivo dell'analisi è determinare l'angolo tra due movimenti all'interno di un sistema articolare, in particolare nell'area di studio della cinematica masticatoria. La comprensione di questi angoli ci consente di:
| |
|
| |
| 1. **Valutare la dinamica mandibolare**: Calcolare gli angoli tra i segmenti mandibolari può fornire informazioni essenziali su come la mandibola si sposta durante il movimento, aiutando a descrivere i pattern del movimento articolare.
| |
|
| |
| 2. **Modellare la biomeccanica del sistema masticatorio**: Gli angoli tra i punti permettono di costruire modelli accurati che simulano il comportamento meccanico del sistema mandibolare, utilizzabili in applicazioni cliniche per diagnosi e trattamenti.
| |
|
| |
| 3. **Confrontare con angoli standard**: Gli angoli misurati possono essere confrontati con valori normali o patologici per identificare eventuali alterazioni nei movimenti mandibolari che potrebbero indicare disturbi dell'articolazione temporomandibolare (ATM).
| |
|
| |
|
| Questo calcolo è fondamentale per fornire una descrizione matematica precisa della cinetica mandibolare e per migliorare la modellazione biomeccanica di strutture orofacciali, cruciali per la diagnosi e l'intervento clinico.
| | Come per i precedenti, la distanza lineare tra il punto <math>1M_m</math> ed il punto <math>7M_m</math> è risultata essere <math>4.81_{mm}</math> mentre l'angolo è stato calcolato come:<math>\theta = \arccos(0.0226) \approx 91.33^\circ</math> Per approfondire la procedura matematica, vedi la spiegazione dettagliata qui{{Tooltip|2=Definizione vettori <math>\vec{1M_m7M_m} = (818.8 - 910.7, -855.1 - (-856.2)) = (-91.9, 1.1)</math>,<math>\vec{1M_mR_p^+} = (912 - 910.7, -741.2 - (-856.2)) = (1.3, 115)</math>. Prodotto scalare: <math>\vec{1M_m7M_m} \cdot \vec{1M_mR_p^+} = (-91.9 \cdot 1.3) + (1.1 \cdot 115) = -119.47 + 126.5 = 7.03</math>. Norme:<math>|\vec{1M_m7M_m}| = \sqrt{(-91.9)^2 + (1.1)^2} \approx 91.92</math>, <math>|\vec{1M_mR_p^+}| = \sqrt{(1.3)^2 + (115)^2} \approx 115.02</math>. Coseno: <math>\cos(\theta) = \frac{7.03}{91.92 \cdot 115.02} \approx 0.000665</math>. Angolo: <math>\theta = \arccos(0.000665) \approx 90^\circ</math>.}} |
| | </Div> |
| | ---- |
Molare mediotrusivo
Osservando il moto cinematico mandibolare a livello del molare mediotrusivo, si nota il cambiamento di direzione angolare rispetto al molare laterotrusivo (

) ed all'incisivo (

). Angolo che tende ad aumentare fino a raggiungere il massimo a livello del condilo (

). L'angolo così formato è conosciuto come angolo di svincolo mediotrusivo tra la cuspide centrale e distale del primo molare.La tabella 4 mostra le distanze tra i punti del tracciato ed il punto

.
| Tabella 4
|
| Tracciato mediotrusivo molare
|
Markers
|
Distanza (mm)
|
Direzione

|
Direzione dinamica

|
| Figura 8: Rappresentazione grafica dei markers rilevati dal 'Replicator' nella masticazione sul lato destro del paziente nell'area inccisale.
|
2
|
0.68
|
Retrusiva
|
Medializzazione
|
| 3
|
2.19
|
Retrusiva
|
Medializzazione
|
| 4
|
3.22
|
Retrusiva
|
Medializzazione
|
| 5
|
5.79
|
Protrusiva
|
Medializzazione
|
| 6
|
7.22
|
Protrusiva
|
Inversione
|
| 7*
|
4.81
|
Retrusiva
|
Lateralizzazione
|
| 8
|
1.18
|
Retrusiva
|
Lateralizzazione
|
|
|
Come per i precedenti, la distanza lineare tra il punto  ed il punto
ed il punto  è risultata essere
è risultata essere  mentre l'angolo è stato calcolato come:
mentre l'angolo è stato calcolato come: Per approfondire la procedura matematica, vedi la spiegazione dettagliata qui
Per approfondire la procedura matematica, vedi la spiegazione dettagliata qui  Definizione vettori
Definizione vettori  ,
, . Prodotto scalare:
. Prodotto scalare:  . Norme:
. Norme: ,
,  . Coseno:
. Coseno:  . Angolo:
. Angolo:  .
.
![]() Definizione vettori ,. Prodotto scalare: . Norme:, . Coseno: . Angolo: .
Definizione vettori ,. Prodotto scalare: . Norme:, . Coseno: . Angolo: .