Difference between revisions of "Store:FLen05"
Gianfranco (talk | contribs) (Created page with "==<!--108-->Fuzzy set <math>\tilde{A}</math> <!--109-->and membership function <math>\mu_{\displaystyle {\tilde {A}}}(x)</math>== <!--110-->We choose - as a formalism - to represent a fuzzy set with the 'tilde':<math>\tilde{A}</math>. <!--111-->A fuzzy set is a set where the elements have a 'degree' of belonging (consistent with fuzzy logic): some can be included in the set at 100%, others in lower percentages. <!--112-->To mathematically represent this degree of belong...") |
Gianfranco (talk | contribs) |
||
| (3 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
== | ==Fuzzy set <math>\tilde{A}</math> and membership function <math>\mu_{\displaystyle {\tilde {A}}}(x)</math>== | ||
We choose - as a formalism - to represent a fuzzy set with the 'tilde':<math>\tilde{A}</math>. A fuzzy set is a set where the elements have a 'degree' of belonging (consistent with fuzzy logic): some can be included in the set at 100%, others in lower percentages. | |||
To mathematically represent this degree of belonging is the function <math>\mu_{\displaystyle {\tilde {A}}}(x)</math> called ''''Membership Function''''. The function <math>\mu_{\displaystyle {\tilde {A}}}(x)</math> is a continuous function defined in the interval <math>[0;1]</math>where it is: | |||
*<math>\mu_ {\tilde {A}}(x) = 1\rightarrow </math | *<math>\mu_ {\tilde {A}}(x) = 1\rightarrow </math> if <math>x</math> is totally contained in <math>A</math> (these points are called 'nucleus', they indicate <u>plausible</u> predicate values). | ||
*<math>\mu_ {\tilde {A}}(x) = 0\rightarrow </math | *<math>\mu_ {\tilde {A}}(x) = 0\rightarrow </math> if <math>x</math> is not contained in <math>A</math> | ||
*<math>0<\mu_ {\tilde {A}}(x) < 1 \;\rightarrow </math | *<math>0<\mu_ {\tilde {A}}(x) < 1 \;\rightarrow </math> if <math>x</math> is partially contained in <math>A</math> (these points are called 'support', they indicate the <u>possible</u> predicate values). | ||
The graphical representation of the function <math>\mu_{\displaystyle {\tilde {A}}}(x)</math> can be varied; from those with linear lines (triangular, trapezoidal) to those in the shape of bells or 'S' (sigmoidal) as depicted in Figure 1, which contains the whole graphic concept of the function of belonging.<ref>{{Cite book | |||
| autore = Zhang W | | autore = Zhang W | ||
| autore2 = Yang J | | autore2 = Yang J | ||
| Line 51: | Line 51: | ||
| OCLC = | | OCLC = | ||
}}</ref> | }}</ref> | ||
[[File:Fuzzy_crisp.svg|alt=|left|thumb|400px|''' | [[File:Fuzzy_crisp.svg|alt=|left|thumb|400px|'''Figure 1:''' Types of graphs for the membership function.]] | ||
The '''support set''' of a fuzzy set is defined as the zone in which the degree of membership results <math>0<\mu_ {\tilde {A}}(x) < 1</math>; <!--131-->on the other hand, the '''core''' is defined as the area in which the degree of belonging assumes value <math>\mu_ {\tilde {A}}(x) = 1</math> | |||
The 'Support set' represents the values of the predicate deemed '''possible''', while the 'core' represents those deemed more '''plausible'''. | |||
If <math>{A}</math> <!--134-->represented a set in the ordinary sense of the term or classical language logic previously described, its membership function could assume only the values <math>1</math> <!--135-->or <math>0</math>, <math>\mu_{\displaystyle {{A}}}(x)= 1 \; \lor \;\mu_{\displaystyle {{A}}}(x)= 0</math> <!--136-->depending on whether the element <math>x</math> <!--137-->belongs to the whole or not, as considered. <!--138-->Figure 2 shows a graphic representation of the crisp (rigidly defined) or fuzzy concept of membership, which clearly recalls Smuts's considerations.<ref name=":0">•SMUTS J.C. 1926, [[wikipedia:Holism_and_Evolution|<!--139-->Holism and Evolution]], London: Macmillan.</ref> | |||
Let us go back to the specific case of our Mary Poppins, in which we see a discrepancy between the assertions of the dentist and the neurologist and we look for a comparison between classical logic and fuzzy logic: | |||
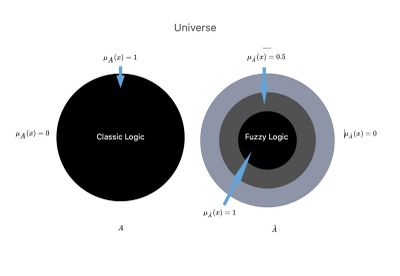
[[File:Fuzzy1.jpg|thumb|400x400px|'''<!--141-->Figure 2:''' <!--142-->Representation of the comparison between a classical and fuzzy ensemble.]] | [[File:Fuzzy1.jpg|thumb|400x400px|'''<!--141-->Figure 2:''' <!--142-->Representation of the comparison between a classical and fuzzy ensemble.]] | ||
''' | '''Figure 2:''' Let us imagine the Science Universe <math>U</math> <!--145-->in which there are two parallel worlds or contexts, <math>{A}</math> <!--146-->and <math>\tilde{A}</math>. | ||
<math>{A}=</math> | <math>{A}=</math> In the scientific context, the so-called ‘crisp’, and we have converted into ''the logic'' of ''Classic Language'', in which the physician has an absolute scientific background information <math>KB</math> <!--148-->with a clear dividing line that we have named <math>KB_c</math>. | ||
<math>\tilde{A}=</math | <math>\tilde{A}=</math> In another scientific context called ‘fuzzy logic’, and in which there is a union between the subset <math>{A}</math> <!--150-->in <math>\tilde{A}</math> <!--151-->that we can go so far as to say: union between <math>KB_c</math>. | ||
We will remarkably notice the following deductions: | |||
*''' | *'''Classical Logic''' in the Dental Context <math>{A}</math> in which only a logical process that gives as results <math>\mu_{\displaystyle {{A}}}(x)= 1 </math> will be possible, or <math>\mu_{\displaystyle {{A}}}(x)= 0 </math> being the range of data <math>D=\{\delta_1,\dots,\delta_4\}</math> reduced to basic knowledge <math>KB</math> in the set <math>{A}</math>. This means that outside the dental world there is a void and that term of set theory is written precisely <math>\mu_{\displaystyle {{A}}}(x)= 0 </math> and which is synonymous with a high range of: | ||
{{q2|Differential diagnostic error|}} | |||
*''' | *'''Fuzzy logic''' in a dental context <math>\tilde{A}</math> in which they are represented beyond the basic knowledge <math>KB</math> of the dental context also those partially acquired from the neurophysiological world <math>0<\mu_ {\tilde {A}}(x) < 1</math> will have the prerogative to return a result <math>\mu_\tilde{A}(x)= 1 | ||
</math | </math> and a result <math>0<\mu_ {\tilde {A}}(x) < 1</math> because of basic knowledge <math>KB</math> which at this point is represented by the union of <math>KB_c</math> dental and neurological contexts. The result of this scientific-clinical implementation of dentistry would allow a {{q2|Reduction of differential diagnostic error|}} | ||
Latest revision as of 17:23, 19 October 2022
Fuzzy set and membership function
We choose - as a formalism - to represent a fuzzy set with the 'tilde':. A fuzzy set is a set where the elements have a 'degree' of belonging (consistent with fuzzy logic): some can be included in the set at 100%, others in lower percentages.
To mathematically represent this degree of belonging is the function called 'Membership Function'. The function is a continuous function defined in the interval where it is:
- if is totally contained in (these points are called 'nucleus', they indicate plausible predicate values).
- if is not contained in
- if is partially contained in (these points are called 'support', they indicate the possible predicate values).
The graphical representation of the function can be varied; from those with linear lines (triangular, trapezoidal) to those in the shape of bells or 'S' (sigmoidal) as depicted in Figure 1, which contains the whole graphic concept of the function of belonging.[1][2]
The support set of a fuzzy set is defined as the zone in which the degree of membership results ; on the other hand, the core is defined as the area in which the degree of belonging assumes value
The 'Support set' represents the values of the predicate deemed possible, while the 'core' represents those deemed more plausible.
If represented a set in the ordinary sense of the term or classical language logic previously described, its membership function could assume only the values or , depending on whether the element belongs to the whole or not, as considered. Figure 2 shows a graphic representation of the crisp (rigidly defined) or fuzzy concept of membership, which clearly recalls Smuts's considerations.[3]
Let us go back to the specific case of our Mary Poppins, in which we see a discrepancy between the assertions of the dentist and the neurologist and we look for a comparison between classical logic and fuzzy logic:
Figure 2: Let us imagine the Science Universe in which there are two parallel worlds or contexts, and .
In the scientific context, the so-called ‘crisp’, and we have converted into the logic of Classic Language, in which the physician has an absolute scientific background information with a clear dividing line that we have named .
In another scientific context called ‘fuzzy logic’, and in which there is a union between the subset in that we can go so far as to say: union between .
We will remarkably notice the following deductions:
- Classical Logic in the Dental Context in which only a logical process that gives as results will be possible, or being the range of data reduced to basic knowledge in the set . This means that outside the dental world there is a void and that term of set theory is written precisely and which is synonymous with a high range of:
- Fuzzy logic in a dental context in which they are represented beyond the basic knowledge of the dental context also those partially acquired from the neurophysiological world will have the prerogative to return a result and a result because of basic knowledge which at this point is represented by the union of dental and neurological contexts. The result of this scientific-clinical implementation of dentistry would allow a «Reduction of differential diagnostic error»
- ↑ Zhang W, Yang J, Fang Y, Chen H, Mao Y, Kumar M, «Analytical fuzzy approach to biological data analysis», in Saudi J Biol Sci, 2017».
PMID:28386181 - PMCID:PMC5372457
DOI:10.1016/j.sjbs.2017.01.027 - ↑ Lazar P, Jayapathy R, Torrents-Barrena J, Mol B, Mohanalin, Puig D, «Fuzzy-entropy threshold based on a complex wavelet denoising technique to diagnose Alzheimer disease», in Healthc Technol Lett, The Institution of Engineering and Technology, 2016».
PMID:30800318 - PMCID:PMC6371778
DOI:10.1049/htl.2016.0022 - ↑ •SMUTS J.C. 1926, Holism and Evolution, London: Macmillan.


![{\displaystyle [0;1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc3bf59a5da5d8181083b228c8933efbda133483)