Difference between revisions of "Store:LTcondilo"

Latest revision as of 18:03, 26 December 2024

Condilo Laterotrusivo

Questo paragrafo illustra un processo matematico per calcolare la distanza e l'angolo formato tra due segmenti in un piano 2D, con applicazione nella cinematica mandibolare. La spiegazione riguarda il calcolo degli angoli tra vettori che rappresentano movimenti articolari, ad esempio i condili durante i movimenti mandibolari (Figura 5 e Tabella 1).

Tabella 1
Tracciato masticatorio	Markers	Distanza (mm)	Direzione $X$	Direzione $Y$
Figura 5: Sovrapposizione dei marker in Geogebra nel tracciato cinematico del condilo laterotrusivo	2	1.734	Protrusiva	Parallela
	3	4.99	Protrusiva	Lateralizzazione
	4	6.59	Protrusiva	Lateralizzazione
	5	3.66	Inversione	Inversione
	6	0.923	Retrusiva	Lateralizzazione
	7*	0.898	Protrsiva	Medializzazione
	8	0.257	Protrusiva	Medializzazione

Osservando la figura e la tabella, possiamo estrapolare le distanze tra i punti marcati ed in particolare segnaliamo che è stato considerato il punto $7L_{c}$ come punto estremo in cui il condilo inverte il moto ed inizia un percorso mediali verso la massima intercuspidazione. Questo punto, anzi, la distanza tra questo punto ed il punto $1L_{c}$ rappresenta il movimento di Bennett. Ad esempio, questa distanza è stata correttamente calcolata come circa $0.898\,_{\text{mm}}$ con una direzione calcolata come:

$\theta =131.87^{\circ }$ ed il corrispettivo $\theta ^{'}=42^{\circ }$

Per chi desidera approfondire il formalismo matematico, riportiamo il calcolo dettagliato nel popup interattivo. Calcolo dettagliato: distanza tra $P_{1}=(58.3,-50.9)$ e $P_{7}=(44,-34.9)$ , distanza euclidea ${\sqrt {(-14.3)^{2}+(16)^{2}}}\approx 21.47\,{\text{pixel}}$ , convertita in mm come $21.47\times 0.04184\approx 0.898\,{\text{mm}}$ , angolo $\theta =\arccos(-0.6665)\approx 131.87^{\circ }$ .

@@ Line 1: / Line 1: @@
-== Distanze e Direzioni ==
+<p>
+'''Condilo Laterotrusivo'''
+</p>
-=== Condilo Laterotrusivo ===
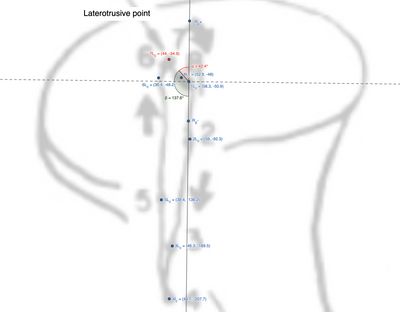
+<Div>Questo paragrafo illustra un processo matematico per calcolare la distanza e l'angolo formato tra due segmenti in un piano 2D, con applicazione nella cinematica mandibolare. La spiegazione riguarda il calcolo degli angoli tra vettori che rappresentano movimenti articolari, ad esempio i condili durante i movimenti mandibolari (Figura 5 e Tabella 1).
-Questo paragrafo illustra un processo matematico utilizzato per calcolare la distanza e l'angolo formato tra due segmenti in un piano 2D, con applicazione nella cinematica mandibolare. La spiegazione riguarda come determinare l'angolo tra due vettori che rappresentano movimenti articolari all'interno di un sistema articolare, ad esempio i condili durante i movimenti della mandibola (Figura 2 e Tabella 1).
-[[File:Angolo laterotrusivo TMJ.jpg|thumb|'''Figura 2:''' Rappresentazione grafica reale dei punti marcati nel ciclo masticatorio{{Rosso inizio}}rifare{{Rosso Fine}}|center|525x525px]]Osservando la figura e la tabella, possiamo estrapolare le distanze dei punti marcati dallo strumenti di replicazione dei movimenti mandibolari e nello specifico la distanza tra il punto 1 e il punto 7 che è stata correttamente calcolata come circa 2.78 mm e con una direzione calcolata con  <math>
+<Center>
-\theta = \arccos(0.840) \approx 33.57^\circ
-</math>. Per gli appassionati e curiosi di seguire il formalismo matematico riportiamo nel popup il contenuto.{{Tooltip|2=Dobbiamo calcolare la distanza euclidea tra i punti <math>P_1 = (59, -58.3)</math> e <math>P_7 = (44, -34.9)</math>. La formula per la distanza euclidea tra due punti <math>(x_1, y_1)</math> e <math>(x_2, y_2)</math> è:<math>\text{distanza} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}</math>'''Sostituendo i valori''':<math>
-\text{distanza} = \sqrt{(44 - 59)^2 + (-34.9 - (-58.3))^2}
-</math><math>\text{distanza} =\sqrt{(-15.0)^2 + (23.4)^2} = \sqrt{225.0 + 547.56} = \sqrt{772.56} \approx 27.78 \, \text{pixel}</math>A questo punto, per convertire in millimetri, moltiplichiamo la distanza in pixel per il fattore di conversione (che supponiamo essere 0.1 mm/pixel, come indicato nel modello):<math>\text{distanza in mm} = 27.78 \times 0.1 = 2.78 \,\text{mm}</math> Ora possiamo usare la formula per il coseno dell'angolo tra i due vettori: <math>\cos(\theta) = \frac{\vec{AB} \cdot \vec{AC}}{|\vec{AB}| \cdot |\vec{AC}|}</math>. Sostituendo i valori: Infine, l'angolo \(\theta\) è calcolato tramite la funzione arccoseno:  <math>\theta = \arccos(0.840) \approx 33.57^\circ  </math>}}
 {| class="wikitable"
-! colspan="4" |Tabella 1
+! colspan="5" |Tabella 1
 |-
-!Punto
+!<small>Tracciato masticatorio</small>
-!Distanza
+!<small>Markers</small>
-(mm)
+!<small>Distanza (mm)</small>
-!Direzione
+!<small>Direzione</small>
-(X - antero-posteriore)
+<small><math>X</math></small>
-!Direzione dinamica
+!<small>Direzione</small> <small><math>Y</math></small>
-(Y - latero-mediale)
+|-
-|-
+| rowspan="9" |[[File:Figura 2 finale mod..jpg|center|400x400px|'''Figura 2:''' Rappresentazione grafica reale dei punti marcati nel ciclo masticatorio]]<small>'''Figura 5:''' Sovrapposizione dei marker in Geogebra nel tracciato cinematico del condilo laterotrusivo</small>
 |2
-|3.40
+|1.734
-|Nessuno
+|Protrusiva
-|Lateralizzazione
+|Parallela
 |-
 |3
-|11.92
+|4.99
-|Avanti
+|Protrusiva
 |Lateralizzazione
 |-
 |4
-|15.75
+|6.59
-|Avanti
+|Protrusiva
 |Lateralizzazione
 |-
 |5
-|8.76
+|3.66
-|Avanti
+|Inversione
+|Inversione
+|-
+|6
+|0.923
+|Retrusiva
 |Lateralizzazione
 |-
-|6
-|2.21
-|Indietro
-|Medializzazione
-|-
 |7*
-|2.78
+|0.898
-|Indietro
+|Protrsiva
 |Medializzazione
 |-
 |8
-|1.20
+|0.257
-|Indietro
+|Protrusiva
-| Medializzazione
+|Medializzazione
 |-
-| colspan="4" |Rappresentazione delle distanze e dell'angolo formato tra i punti marcati nel ciclo masticatorio riferiti al punto 1 di massima intercuspidazione. Il punto 7* è il punto considerato per lo specifico calcolo del condilo laterotrusivo. La direzione mediale o laterale del tracciato va considerato rispetto all'asseperpendicolare ed  intersecante il punto <math>
+| colspan="4" |
-L
+|-
-</math> , per cui in questo caso tutti i punti da 2 a 4 hanno un andamento di moto lateralizzante e cioè si spostano da mediale a laterale mentre dai punti 6 a 1 il moto è medializzante, cioè inizia il percorso di ritorno al p unto di partenza di massima intercuspidazione.
+|}
-|}
+</Center>
+Osservando la figura e la tabella, possiamo estrapolare le distanze tra i punti marcati ed in particolare segnaliamo che è stato considerato il punto <math>7L_c</math>  come punto estremo in cui il condilo inverte il moto ed inizia un percorso mediali verso la massima intercuspidazione. Questo punto, anzi, la distanza tra questo punto ed il punto <math>1L_c</math>  rappresenta il movimento di Bennett. Ad esempio, questa distanza è stata correttamente calcolata come circa <math>0.898 \, _\text{mm}</math> con una direzione calcolata come:
+<math>\theta = 131.87^\circ </math> ed il corrispettivo <math>\theta^' = 42^\circ </math>
+Per chi desidera approfondire il formalismo matematico, riportiamo il calcolo dettagliato nel popup interattivo.{{Tooltip|2=Calcolo dettagliato: distanza tra <math>P_1 = (58.3, -50.9)</math> e <math>P_7 = (44, -34.9)</math>, distanza euclidea <math>\sqrt{(-14.3)^2 + (16)^2} \approx 21.47 \, \text{pixel}</math>, convertita in mm come <math>21.47 \times 0.04184 \approx 0.898 \, \text{mm}</math>, angolo <math>\theta = \arccos(-0.6665) \approx 131.87^\circ</math>.}}
+</Div>
+----