|
|
| (18 intermediate revisions by the same user not shown) |
| Line 1: |
Line 1: |
| ==Mediotrusive== | | ===Condilo Mediotrusivo=== |
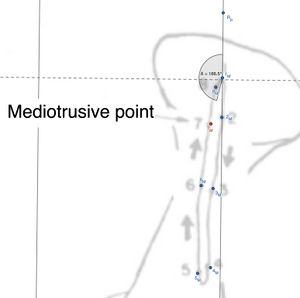
| [[File:Mediotrusive angle.jpeg|left|thumb|300x300px]] | | '''Descrizione focalizzata dell'analisi matematica dei punti''' |
| | |
| | * '''Punti e coordinate coinvolte''' |
| | ** Nel contesto della nostra analisi, abbiamo tre punti nello spazio 2D che ci interessano: |
| | ** Coordinate <math>P1_{M}</math> del punto 1 del condilo mediotrusivo: <math>(1164.1, -64.2)</math> |
| | **Coordinate <math>P7_{M}</math> del punto 7 del condilo mediotrusivo: <math>(1148.2, -124.6)</math> |
| | **Coordinate <math>R_p</math> del punto di riferimento del condilo mediotrusivo: <math>(1165, 11.4)</math> |
| | |
| | |
| | |
| | Questi punti rappresentano tre posizioni specifiche all'interno di un sistema articolare che stiamo studiando, con l'obiettivo di calcolare l'angolo tra il segmento che unisce i punti <math>P1_{M}</math> e <math>P7_{M}</math>, e il segmento che unisce i punti <math>P1_{M}</math> e <math>R_p</math>. Questo tipo di analisi è comune nella modellazione di movimenti articolari per comprendere come si muovono i segmenti di un sistema rispetto a un punto di riferimento, come nel caso di un sistema masticatorio. [[File:Mediotrusive angle.jpeg|left|thumb|300x300px]] |
| <br /> | | <br /> |
| | |
| {| class="wikitable" | | {| class="wikitable" |
| |- | | |- |
| !Punto!!Distanza (pixel)!!Distanza (mm)!!Direzione in X | | !Punto!!Distanza |
| | (mm) |
| | !Direzione in X |
| (antero-posteriore) | | (antero-posteriore) |
| !Direzione in Y | | !Direzione in Y |
| (latero-mediale) | | (latero-mediale) |
| |- | | |- |
| |2||50.92||5.09||Indietro||Mediale | | |2||5.09||Protrusiva |
| | |Mediale |
| |- | | |- |
| |3||148.05||14.81||Indietro||Mediale | | |3||14.81 |
| | |Protrusiva||Mediale |
| |- | | |- |
| |4||255.81||25.58||Indietro||Mediale | | |4 |
| | |25.58||Protrusiva||Mediale |
| |- | | |- |
| |5||265.43||26.54||Indietro||Mediale | | |5||26.54||Protrusiva||Mediale |
| |- | | |- |
| |6||145.68||14.57||Indietro||Mediale | | |6||14.57||Protrusiva |
| | |Mediale |
| |- | | |- |
| |7||62.45||6.25||Indietro||Mediale | | |7*||6.25||Protrusiva|| Mediale |
| |- | | |- |
| |8||11.87||1.19||Indietro||Mediale | | |8 ||1.19||Protrusiva||Mediale |
| |} | | |} |
|
| |
|
| |
| ===Descrizione focalizzata dell'analisi matematica dei punti===
| |
|
| |
| ====Punti e coordinate coinvolte====
| |
|
| |
| Nel contesto della nostra analisi, abbiamo tre punti nello spazio 2D che ci interessano:
| |
|
| |
| *Coordinate <math>
| |
| P1_{M}
| |
| </math> del punto 1 del condilo mediotrusivo: <math>
| |
| (1164.1, -64.2)
| |
| </math>
| |
| *Coordinate <math>
| |
| P7_{M}
| |
| </math> del punto 7 del condilo mediotrusivo: <math>
| |
| (1148.2, -124.6)
| |
| </math>
| |
| *Coordinate <math>
| |
| H3 _{M}
| |
| </math> del punto di riferimento del condilo mediotrusivo: <math>
| |
| (1165, 11.4)
| |
| </math>
| |
|
| |
| Questi punti rappresentano tre posizioni specifiche all'interno di un sistema articolare che stiamo studiando, con l'obiettivo di calcolare l'angolo tra il segmento che unisce i punti <math>
| |
| P1_{M}
| |
| </math>e <math>
| |
| P7_{M}
| |
| </math>, e il segmento che unisce i punti <math>
| |
| P1_{M}
| |
| </math>e <math>
| |
| H3 _{M}
| |
| </math>. Questo tipo di analisi è comune nella modellazione di movimenti articolari per comprendere come si muovono i segmenti di un sistema rispetto a un punto di riferimento, come nel caso di un sistema masticatorio.
| |
|
| |
|
| ====Iter matematico per il calcolo dell'angolo==== | | ====Iter matematico per il calcolo dell'angolo==== |
|
| |
|
| L'angolo tra due segmenti può essere calcolato utilizzando la **trigonometria vettoriale** e, in particolare, il **prodotto scalare**. Questo metodo è utile quando vogliamo determinare la relazione angolare tra due movimenti distinti nello spazio. | | L'angolo tra due segmenti può essere calcolato utilizzando la trigonometria vettoriale {{Tooltip|2=Innanzitutto, dobbiamo calcolare i vettori che rappresentano i segmenti tra i punti: Il vettore tra il punto <math>P1_{M}</math> e il punto <math>P7_{M}</math>: <math>\vec{AB} = P7_{M}-P1_{M}=(1148.2,-124.6)-(1164.1,-64.2)=(-15.9,-60.4)</math>. Il vettore tra il punto <math>P1_{M}</math> e il punto di riferimento <math>R_p</math>: <math>\vec{AC}=R_p-P1_{M}=(1165,11.4)-(1164.1,-64.2)=(0.9,75.6)</math>.Questo metodo ci permette di rappresentare le relazioni angolari tra movimenti distinti nello spazio.|3=2}} ed il prodotto scalare {{Tooltip|2=Il prodotto scalare tra due vettori <math>\vec{AB}</math> e <math>\vec{AC}</math> è dato dalla formula: <math>\vec{AB} \cdot \vec{AC} = AB_x \cdot AC_x + AB_y \cdot AC_y</math>. Sostituendo i valori calcolati: <math>\vec{AB} \cdot \vec{AC} = (-15.9) \cdot (0.9) + (-60.4) \cdot (75.6) = -14.31 - 4566.24 = -4580.55</math>.Una volta eseguiti i passaggi trigonometrici e il prodotto scalare, si passa al calcolo della lunghezza del vettore: <math>|\vec{AB}| = \sqrt{AB_x^2 + AB_y^2} = \sqrt{(-15.9)^2 + (-60.4)^2} = \sqrt{252.81 + 3648.16} = \sqrt{3900.97} \approx 62.45</math>.|3=2}} |
| | |
| ====1. Definizione dei vettori====
| |
| | |
| Innanzitutto, dobbiamo calcolare i vettori che rappresentano i segmenti tra i punti: | |
| | |
| *Il vettore tra il punto <math>
| |
| P1_{M} | |
| </math>e il punto <math> | |
| P7_{M} | |
| </math>: | |
| | |
| <math> | |
| \vec{AB} = P7_{M} - P1_{M} | |
| = (1148.2, -124.6) - (1164.1, -64.2) = (-15.9, -60.4)
| |
| </math> | |
| | |
| *Il vettore tra il punto 1<sub>Lm</sub> e il punto H₃:
| |
| | |
| <math> | |
| \vec{AC} =H3_{M}-P1_{M} | |
| = (1165, 11.4) - (1164.1, -64.2) = (0.9, 75.6) | |
| | |
| </math> | |
| | |
| ====2. Prodotto scalare====
| |
| | |
| Il **prodotto scalare** tra due vettori \(\vec{AB}\) e \(\vec{AC}\) è dato dalla formula: | |
| | |
| <math> | |
| \vec{AB} \cdot \vec{AC} = AB_x \cdot AC_x + AB_y \cdot AC_y | |
| </math> | |
| | |
| Sostituendo i valori calcolati: | |
| | |
| <math> | |
| \vec{AB} \cdot \vec{AC} = (-15.9) \cdot (0.9) + (-60.4) \cdot (75.6) = -14.31 + (-4566.24) = -4580.55 | |
| </math> | |
| | |
| ====3. Calcolo delle norme====
| |
| | |
| Le norme (lunghezze) dei due vettori sono calcolate con la formula della lunghezza del vettore:
| |
| | |
| <math> | |
| |\vec{AB}|=\sqrt{AB_x^2 + AB_y^2} = \sqrt{(-15.9)^2 + (-60.4)^2} = \sqrt{252.81 + 3648.16} = \sqrt{3900.97} \approx 62.45 | |
| </math> | |
| | |
| <math>
| |
| |\vec{AC}| = \sqrt{AC_x^2 + AC_y^2} = \sqrt{(0.9)^2 + (75.6)^2} = \sqrt{0.81 + 5710.56} = \sqrt{5711.37} \approx 75.58
| |
| </math>
| |
| | |
| ====4. Calcolo dell'angolo====
| |
| | |
| Ora possiamo usare la formula per il coseno dell'angolo tra i due vettori:
| |
| | |
| <math>
| |
| \cos(\theta) = \frac{\vec{AB} \cdot \vec{AC}}{|\vec{AB}| \cdot |\vec{AC}|}
| |
| </math>
| |
| | |
| Sostituendo i valori:
| |
| | |
| <math>
| |
| \cos(\theta) = \frac{-4580.55}{62.45 \cdot 75.58} = \frac{-4580.55}{4717.25} \approx -0.971
| |
| </math>
| |
| | |
| Infine, l'angolo \(\theta\) è calcolato tramite la funzione arcoseno:
| |
| | |
| <math>
| |
| \theta = \arccos(-0.971) \approx 166.43^\circ
| |
| </math>
| |
| | |
| ====Motivo dell'analisi====
| |
| | |
| L'obiettivo dell'analisi è determinare l'angolo tra due movimenti all'interno di un sistema articolare, in particolare nell'area di studio della cinematica masticatoria. La comprensione di questi angoli ci consente di:
| |
| | |
| 1. **Valutare la dinamica mandibolare**: Calcolare gli angoli tra i segmenti mandibolari può fornire informazioni essenziali su come la mandibola si sposta durante il movimento, aiutando a descrivere i pattern del movimento articolare.
| |
|
| |
| 2. **Modellare la biomeccanica del sistema masticatorio**: Gli angoli tra i punti permettono di costruire modelli accurati che simulano il comportamento meccanico del sistema mandibolare, utilizzabili in applicazioni cliniche per diagnosi e trattamenti.
| |
|
| |
| 3. **Confrontare con angoli standard**: Gli angoli misurati possono essere confrontati con valori normali o patologici per identificare eventuali alterazioni nei movimenti mandibolari che potrebbero indicare disturbi dell'articolazione temporomandibolare (ATM). | |
| | |
| Questo calcolo è fondamentale per fornire una descrizione matematica precisa della cinetica mandibolare e per migliorare la modellazione biomeccanica di strutture orofacciali, cruciali per la diagnosi e l'intervento clinico.
| |
| | |
| ==Conclusione==
| |
| l tracciato lateroretrusivo del punto molare laterotrusivo, anziché un arco puramente laterale, suggerisce un'interazione complessa tra il condilo laterotrusivo e il movimento del condilo mediotrusivo. Questo fenomeno può essere spiegato come un’interferenza causata dal tragitto orbitante del condilo mediotrusivo, oltre che da una componente retrusiva intrinseca al condilo laterotrusivo stesso.
| |
| | |
| ===Analisi delle Possibili Cause:===
| |
| | |
| #'''Interferenza del Condilo Medioretrusivo''': Il condilo mediotrusivo, che segue un percorso orbitante durante i movimenti laterali, potrebbe condizionare indirettamente il percorso del condilo laterotrusivo e, di conseguenza, del punto molare laterotrusivo. Il condilo mediotrusivo, infatti, non si limita a muoversi verso l'interno, ma segue una traiettoria che presenta componenti di traslazione e rotazione complesse. Questo movimento orbitale genera una sorta di “effetto leva” sul lato opposto, inducendo un '''movimento di retrazione passiva''' del condilo laterotrusivo, che si traduce nel tracciato lateroretrusivo del molare laterotrusivo.
| |
| #'''Componente Retrusiva Intrinseca del Condilo Laterotrusivo''': L’angolo di rotazione del condilo laterotrusivo potrebbe includere una componente retrusiva, ma questa da sola non giustificherebbe completamente il tracciato lateroretrusivo osservato. Tuttavia, la presenza di un movimento retrusivo secondario può essere amplificata dal tragitto orbitante del condilo mediotrusivo, creando un effetto sinergico che forza il punto molare laterotrusivo a seguire un tracciato non puramente laterale.
| |
| | |
| ===Perché Questo Punto Non è Immediatamente Evidente:===
| |
| Il motivo per cui questo punto critico non è evidente subito risiede nella '''combinazione dei movimenti dei condili''', che sono difficili da percepire come una '''dinamica unitaria'''. A prima vista, sembra naturale attribuire il tracciato lateroretrusivo del molare laterotrusivo alla rotazione composta del condilo lavorante. Tuttavia, il ruolo del condilo mediotrusivo, con il suo movimento orbitante, è un contributo nascosto che agisce passivamente ma in modo determinante. La complessità deriva dalla '''natura tridimensionale e simultanea del movimento mandibolare''', che rende difficile isolare immediatamente l’influenza di ciascun condilo.
| |
| | |
| In sostanza, la presenza del tragitto orbitante del condilo mediotrusivo introduce una '''componente di retrazione passiva''' che si somma alla rotazione laterale del condilo lavorante, portando a un tracciato lateroretrusivo del punto molare laterotrusivo.
| |
| | |
| ==Analisi Matematica della Componente Lateroretrusiva del Punto Molarare Laterotrusivo==
| |
| | |
| Per rappresentare matematicamente l'interazione tra i condili e il tracciato del punto molare laterotrusivo, possiamo sviluppare un formalismo che modelli i movimenti complessi dei condili e l'effetto risultante sul punto molare laterotrusivo.
| |
| | |
| ===1. Coordinate dei Condili e del Punto Molarare===
| |
| | |
| Consideriamo le coordinate dei condili e del punto molare laterotrusivo nel sistema di riferimento cartesiano tridimensionale (asse X per l'orientamento antero-posteriore, asse Y per la laterolateralità e asse Z per l'altezza).
| |
| | |
| Definiamo:
| |
| *<math>\mathbf{C}_L(t) = (x_L(t), y_L(t), z_L(t))</math>: coordinate del condilo laterotrusivo al tempo <math>t</math>.
| |
| *<math>\mathbf{C}_M(t) = (x_M(t), y_M(t), z_M(t))</math>: coordinate del condilo mediotrusivo al tempo <math>t</math>.
| |
| *<math>\mathbf{M}_L(t) = (x_{m_L}(t), y_{m_L}(t), z_{m_L}(t))</math>: coordinate del punto molare laterotrusivo al tempo <math>t</math>.
| |
| | |
| ===2. Rotazione e Traslazione dei Condili===
| |
| | |
| ====Condilo Laterotrusivo (Lavorante)====
| |
| Il movimento del condilo laterotrusivo può essere descritto come una combinazione di rotazione (angolo laterotrusivo <math>\theta_L</math>) e traslazione retrusiva <math>d_L</math>, dove:
| |
| *<math>\theta_L(t)</math> è l'angolo di rotazione laterale,
| |
| *<math>d_L</math> è la componente retrusiva della traslazione del condilo laterotrusivo, dovuta al movimento del condilo mediotrusivo.
| |
| | |
| La posizione del condilo laterotrusivo può essere descritta come:
| |
| <math>
| |
| \mathbf{C}_L(t) = \mathbf{C}_L(0) + R(\theta_L) \cdot (x_{L}, y_{L}, z_{L}) + \mathbf{d}_L
| |
| </math>
| |
| dove <math>R(\theta_L)</math> è la matrice di rotazione intorno a un asse <math>Y</math> inclinato in base all’angolo laterotrusivo <math>\theta_L</math>, e <math>\mathbf{d}_L = (-d_L, 0, 0)</math> rappresenta la componente di retrazione sul piano X.
| |
| | |
| ====Condilo Mediotrusivo (Non Lavorante)====
| |
| Il condilo mediotrusivo segue un movimento orbitante che possiamo rappresentare con una rotazione e una traslazione. La rotazione del condilo mediotrusivo viene espressa con un angolo orbitante <math>\theta_M</math>, tale che:
| |
| <math>
| |
| \mathbf{C}_M(t) = \mathbf{C}_M(0) + R(\theta_M) \cdot (x_{M}, y_{M}, z_{M})
| |
| </math>
| |
| con <math>R(\theta_M)</math> come matrice di rotazione che descrive la traiettoria orbitale mediotrusiva.
| |
| | |
| ===3. Tracciato del Punto Molarare Laterotrusivo===
| |
| | |
| Il tracciato del punto molare laterotrusivo è condizionato sia dalla rotazione retrusiva del condilo laterotrusivo che dal tragitto orbitante del condilo mediotrusivo. La posizione risultante del punto molare laterotrusivo, <math>\mathbf{M}_L(t)</math>, può essere modellata come la somma vettoriale della sua posizione iniziale e degli spostamenti dovuti a ciascun condilo:
| |
| <math>
| |
| \mathbf{M}_L(t) = \mathbf{M}_L(0) + R(\theta_L) \cdot \mathbf{M}_L(0) + \alpha \cdot \mathbf{C}_L(t) + \beta \cdot \mathbf{C}_M(t)
| |
| </math>
| |
| dove:
| |
| *<math>R(\theta_L)</math> rappresenta la rotazione laterale del condilo laterotrusivo,
| |
| *<math>\alpha</math> e <math>\beta</math> sono coefficienti che indicano l’influenza proporzionale dei movimenti dei condili laterotrusivo e mediotrusivo sul tracciato del punto molare laterotrusivo.
| |
| | |
| ===4. Formalizzazione della Componente Lateroretrusiva===
| |
| | |
| Per descrivere la componente lateroretrusiva, l’effetto orbitante del condilo mediotrusivo introduce una forza vettoriale aggiuntiva nel movimento del punto molare laterotrusivo:
| |
| <math>
| |
| \mathbf{M}_{L,\text{ret}}(t) = \beta \cdot \mathbf{C}_M(t) + (-d_L, 0, 0)
| |
| </math>
| |
| dove <math>\mathbf{M}_{L,\text{ret}}(t)</math> rappresenta il tracciato effettivo lateroretrusivo dovuto all’interazione tra la retrazione del condilo lavorante e il percorso orbitale del condilo mediotrusivo.
| |
| | |
| ===Interpretazione===
| |
| | |
| Questo formalismo evidenzia che il tracciato lateroretrusivo del punto molare laterotrusivo è determinato sia dalla **componente retrusiva** (presente nel movimento del condilo lavorante) sia dall'**influenza orbitante del condilo mediotrusivo** (che altera passivamente il percorso del molare laterotrusivo).
| |
| | |
| Considerando il formalismo matematico e la complessità dei movimenti condilari, la domanda se esista un asse cerniera verticale "puro" si rivela più complessa di quanto possa sembrare a prima vista. In effetti, l’idea di un asse cerniera verticale puro, come una linea immutabile intorno alla quale la mandibola ruota esclusivamente in senso verticale, è difficilmente compatibile con la '''dinamica tridimensionale e coordinata dei condili'''.
| |
| | |
| === Analisi della Purezza dell'Asse Cerniera ===
| |
| La presenza di un asse cerniera puro presupporrebbe:
| |
|
| |
|
| # '''Rotazione perfettamente bilanciata''' dei condili, senza influenze reciproche tra loro.
| | Ora possiamo usare la formula per il coseno dell'angolo tra i due vettori {{Tooltip|2=<math>\cos(\theta) = \frac{\vec{AB} \cdot \vec{AC}}{|\vec{AB}| \cdot |\vec{AC}|}</math>. Sostituendo i valori: <math>\cos(\theta) = \frac{-4580.55}{62.45 \cdot 75.58} = \frac{-4580.55}{4717.25} \approx -0.971</math><nowiki>.|3=2}} |
| # '''Assenza di movimenti traslatori''' o orbitali che interferiscano, imponendo variazioni direzionali sul tracciato dei punti di riferimento mandibolari, come i molari e gli incisivi.
| |
|
| |
|
| Tuttavia, come emerso dalla nostra analisi:
| | L'angolo <math>\theta</math> è calcolato tramite la funzione arccoseno: |
|
| |
|
| * '''Il movimento orbitale del condilo mediotrusivo influenza passivamente il condilo laterotrusivo''', inducendo una componente retrusiva che modifica il tracciato del molare laterotrusivo e rende impossibile una rotazione esclusivamente verticale.
| | <math>\theta = \arccos(-0.971) \approx 166.43^\circ</math>. |
| * '''L’interazione reciproca tra i condili crea un effetto sinergico''', nel quale ciascun condilo non opera in isolamento ma è costretto a seguire un movimento composito, regolato da vincoli articolari e muscolari, che rende intrinsecamente asimmetrica la dinamica rotazionale.
| |
|
| |
|
| === Conclusione ===
| | Infine, sottraendo questo angolo da 180°, otteniamo un angolo di <math>13.57^\circ</math>, noto come '''Angolo di Bennett'''. |
| Alla luce di queste osservazioni, la nozione di un asse cerniera verticale puro nella mandibola appare un’idealizzazione, utile in teoria per semplificare i modelli di movimento ma che raramente trova riscontro nella complessità anatomica e funzionale reale.
| |
|
| |
|
| In termini di intelligenza sia umana che artificiale, è più appropriato parlare di un '''"asse di rotazione virtuale e variabile"''' che risulta dalla media dinamica dei movimenti condilari. Questo asse virtuale rappresenta la traiettoria funzionale più probabile intorno alla quale si organizza la rotazione mandibolare, anche se non è mai perfettamente verticale o fisso. È dunque un esempio di come il sistema mandibolare realizzi un '''compromesso biomeccanico''' che garantisce funzionalità e stabilità articolare, pur non rispettando un asse cerniera verticale "puro".
| |
|
| |
|
| In sintesi, il concetto di asse cerniera verticale puro rimane una semplificazione utile, ma nel contesto reale della mandibola, siamo di fronte a un '''asse cerniera funzionale, flessibile e adattivo''', modellato dalle interazioni simultanee e complesse dei condili. Questo rappresenta una perfetta sintesi della complessità della biomeccanica umana, alla quale i modelli matematici e le intelligenze artificiali possono solo avvicinarsi, ma non replicare nella sua totalità.
| |
|
| |
|
| | '''Conclusione della Cinematica Condilare Mediortusiva''' |
|
| |
|
| | Nel sistema masticatorio, il condilo mediotrusivo segue una traiettoria complessa che contribuisce all'equilibrio dinamico durante i movimenti mandibolari laterali. I punti analizzati <math>P1_{M}</math>, <math>P7_{M}</math> e il punto di riferimento <math>R_p</math> rappresentano posizioni articolari chiave lungo il tragitto del condilo mediotrusivo. Studiare questi punti permette di calcolare l'angolo tra due segmenti definiti, essenziali per comprendere i vettori di forza e l'orientamento della mandibola in movimento. In sintesi, l’angolo calcolato tra i punti analizzati del condilo mediotrusivo non solo rappresenta un parametro meccanico, ma funge da indicatore di stabilità e simmetria del sistema masticatorio. Le variazioni angolari rispetto al valore fisiologico suggeriscono l’esistenza di forze anomale o alterazioni che possono influenzare la cinematica mandibolare e potenzialmente contribuire a patologie articolari, offrendo un potenziale punto di osservazione per diagnosi più accurate e interventi clinici mirati. |
| <br /> | | <br /> |
Condilo Mediotrusivo
Descrizione focalizzata dell'analisi matematica dei punti
- Punti e coordinate coinvolte
- Nel contesto della nostra analisi, abbiamo tre punti nello spazio 2D che ci interessano:
- Coordinate
del punto 1 del condilo mediotrusivo: 
- Coordinate
del punto 7 del condilo mediotrusivo: 
- Coordinate
del punto di riferimento del condilo mediotrusivo: 
Questi punti rappresentano tre posizioni specifiche all'interno di un sistema articolare che stiamo studiando, con l'obiettivo di calcolare l'angolo tra il segmento che unisce i punti e , e il segmento che unisce i punti e . Questo tipo di analisi è comune nella modellazione di movimenti articolari per comprendere come si muovono i segmenti di un sistema rispetto a un punto di riferimento, come nel caso di un sistema masticatorio.
| Punto |
Distanza
(mm)
|
Direzione in X
(antero-posteriore)
|
Direzione in Y
(latero-mediale)
|
| 2 |
5.09 |
Protrusiva
|
Mediale
|
| 3 |
14.81
|
Protrusiva |
Mediale
|
| 4
|
25.58 |
Protrusiva |
Mediale
|
| 5 |
26.54 |
Protrusiva |
Mediale
|
| 6 |
14.57 |
Protrusiva
|
Mediale
|
| 7* |
6.25 |
Protrusiva |
Mediale
|
| 8 |
1.19 |
Protrusiva |
Mediale
|
Iter matematico per il calcolo dell'angolo
L'angolo tra due segmenti può essere calcolato utilizzando la trigonometria vettoriale 
Innanzitutto, dobbiamo calcolare i vettori che rappresentano i segmenti tra i punti: Il vettore tra il punto e il punto : 
. Il vettore tra il punto e il punto di riferimento : 
.Questo metodo ci permette di rappresentare le relazioni angolari tra movimenti distinti nello spazio. ed il prodotto scalare Il prodotto scalare tra due vettori 
e 
è dato dalla formula: 
. Sostituendo i valori calcolati: 
.Una volta eseguiti i passaggi trigonometrici e il prodotto scalare, si passa al calcolo della lunghezza del vettore: 
.
Ora possiamo usare la formula per il coseno dell'angolo tra i due vettori 
. Sostituendo i valori: 
<nowiki>.
L'angolo 
è calcolato tramite la funzione arccoseno:
.
Infine, sottraendo questo angolo da 180°, otteniamo un angolo di 
, noto come Angolo di Bennett.
Conclusione della Cinematica Condilare Mediortusiva
Nel sistema masticatorio, il condilo mediotrusivo segue una traiettoria complessa che contribuisce all'equilibrio dinamico durante i movimenti mandibolari laterali. I punti analizzati , e il punto di riferimento rappresentano posizioni articolari chiave lungo il tragitto del condilo mediotrusivo. Studiare questi punti permette di calcolare l'angolo tra due segmenti definiti, essenziali per comprendere i vettori di forza e l'orientamento della mandibola in movimento. In sintesi, l’angolo calcolato tra i punti analizzati del condilo mediotrusivo non solo rappresenta un parametro meccanico, ma funge da indicatore di stabilità e simmetria del sistema masticatorio. Le variazioni angolari rispetto al valore fisiologico suggeriscono l’esistenza di forze anomale o alterazioni che possono influenzare la cinematica mandibolare e potenzialmente contribuire a patologie articolari, offrendo un potenziale punto di osservazione per diagnosi più accurate e interventi clinici mirati.
