Difference between revisions of "Store:AC36mediotrusivo"
| Line 66: | Line 66: | ||
</math>e <math> | </math>e <math> | ||
R_p | R_p | ||
</math> Questo tipo di analisi è comune nella modellazione di movimenti articolari per comprendere come si muovono i segmenti di un sistema rispetto a un punto di riferimento, come nel caso di un sistema masticatorio. Lo stesso formalismo matematico dei precedente con ovvimanete, dati diversi si definiranno i vettori{{Tooltip|2=Innanzitutto, dobbiamo calcolare i vettori che rappresentano i segmenti tra i punti: Il vettore tra | </math> Questo tipo di analisi è comune nella modellazione di movimenti articolari per comprendere come si muovono i segmenti di un sistema rispetto a un punto di riferimento, come nel caso di un sistema masticatorio. Lo stesso formalismo matematico dei precedente con ovvimanete, dati diversi si definiranno i vettori{{Tooltip|2=Innanzitutto, dobbiamo calcolare i vettori che rappresentano i segmenti tra i punti:*Il vettore tra ilpunto <math>P1_{mm} </math> e il punto <math>P7_{mm} </math>:<math>\vec{AB} = P7_{mm} - P1_{mm} = (817.2, -853.5) - (907.1, -852.5) = (-89.9, -1.0)</math> *Il vettore tra il punto <math> P1_{mm} </math> e ilpunto <math> R_p</math>: <math>\vec{AC} = R_p - P1_{mm} = (908.8, -711.5) - (907.1, -852.5) = (1.7, 141.0)</math>}} il prodotto scalare {{Tooltip|2=s}} l calcolo della norma{{Tooltip|2=s}} e l'angolo {{Tooltip|2=d}}. | ||
\vec{AC} = | |||
====Iter matematico per il calcolo dell'angolo==== | ====Iter matematico per il calcolo dell'angolo==== | ||
| Line 78: | Line 77: | ||
*Il vettore tra il punto <math> | *Il vettore tra il punto <math> | ||
P1m_{cl} | |||
</math> e il punto <math> | </math> e il punto <math> | ||
P7 m_{cl} | |||
</math>: | </math>: | ||
<math> | <math> | ||
\vec{AB} = | \vec{AB} = P7 m_{cl} - P1m_{cl} = (817.2, -853.5) - (907.1, -852.5) = (-89.9, -1.0) | ||
</math> | </math> | ||
*Il vettore tra il punto <math> | *Il vettore tra il punto <math> | ||
P1m_{cl} | |||
</math>e il punto <math> | </math>e il punto <math> | ||
H3m_{cl} | |||
</math>: | </math>: | ||
<math> | <math> | ||
\vec{AC} = | \vec{AC} = H3m_{cl} - P1m_{cl} = (908.8, -711.5) - (907.1, -852.5) = (1.7, 141.0) | ||
</math> | </math> | ||
Revision as of 18:22, 1 November 2024
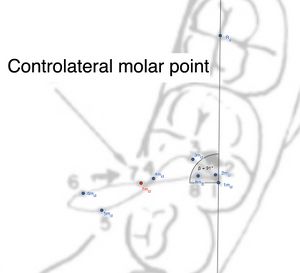
Molare controlaterale
| Punto | Distanza (mm) | Direzione in X
(antero-posteriore) |
Direzione in Y
(latero-mediale) |
|---|---|---|---|
| 2 | 1.11 | Avanti | Laterale |
| 3 | 3.89 | Avanti | Laterale |
| 4 | 7.76 | Avanti | Laterale |
| 5 | 13.75 | Avanti | Laterale |
| 6 | 15.71 | Indietro | Laterale |
| 7* | 8.99 | Indietro | Laterale |
| 8 | 2.43 | Indietro | Laterale |
Come per i precedenti abbiamo tre punti nello spazio 2D che ci interessano e cioè il punto ( punto 1 del molare mediotrusivo), il ( punto 7 del molare mediotrusivo) e del punto di riferimento
- Coordinate
- Coordinate
- Coordinate
Questi punti rappresentano tre posizioni specifiche all'interno di un sistema masticatorio che stiamo studiando, con l'obiettivo di calcolare l'angolo tra il segmento che unisce i punti e , e il segmento che unisce i punti e Questo tipo di analisi è comune nella modellazione di movimenti articolari per comprendere come si muovono i segmenti di un sistema rispetto a un punto di riferimento, come nel caso di un sistema masticatorio. Lo stesso formalismo matematico dei precedente con ovvimanete, dati diversi si definiranno i vettori ![]() Innanzitutto, dobbiamo calcolare i vettori che rappresentano i segmenti tra i punti:*Il vettore tra ilpunto e il punto : *Il vettore tra il punto e ilpunto : il prodotto scalare
Innanzitutto, dobbiamo calcolare i vettori che rappresentano i segmenti tra i punti:*Il vettore tra ilpunto e il punto : *Il vettore tra il punto e ilpunto : il prodotto scalare ![]() s l calcolo della norma
s l calcolo della norma ![]() s e l'angolo
s e l'angolo ![]() d.
d.
Iter matematico per il calcolo dell'angolo
L'angolo tra due segmenti può essere calcolato utilizzando la **trigonometria vettoriale** e, in particolare, il **prodotto scalare**. Questo metodo è utile quando vogliamo determinare la relazione angolare tra due movimenti distinti nello spazio.
1. Definizione dei vettori
Innanzitutto, dobbiamo calcolare i vettori che rappresentano i segmenti tra i punti:
- Il vettore tra il punto e il punto :
- Il vettore tra il punto e il punto :
2. Prodotto scalare
Il **prodotto scalare** tra due vettori \(\vec{AB}\) e \(\vec{AC}\) è dato dalla formula:
Sostituendo i valori calcolati:
3. Calcolo delle norme
Le norme (lunghezze) dei due vettori sono calcolate con la formula della lunghezza del vettore:
4. Calcolo dell'angolo
Ora possiamo usare la formula per il coseno dell'angolo tra i due vettori:
Sostituendo i valori:
Infine, l'angolo \(\theta\) è calcolato tramite la funzione arcoseno:
Motivo dell'analisi
L'obiettivo dell'analisi è determinare l'angolo tra due movimenti all'interno di un sistema articolare, in particolare nell'area di studio della cinematica masticatoria. La comprensione di questi angoli ci consente di:
1. **Valutare la dinamica mandibolare**: Calcolare gli angoli tra i segmenti mandibolari può fornire informazioni essenziali su come la mandibola si sposta durante il movimento, aiutando a descrivere i pattern del movimento articolare.
2. **Modellare la biomeccanica del sistema masticatorio**: Gli angoli tra i punti permettono di costruire modelli accurati che simulano il comportamento meccanico del sistema mandibolare, utilizzabili in applicazioni cliniche per diagnosi e trattamenti.
3. **Confrontare con angoli standard**: Gli angoli misurati possono essere confrontati con valori normali o patologici per identificare eventuali alterazioni nei movimenti mandibolari che potrebbero indicare disturbi dell'articolazione temporomandibolare (ATM).
Questo calcolo è fondamentale per fornire una descrizione matematica precisa della cinetica mandibolare e per migliorare la modellazione biomeccanica di strutture orofacciali, cruciali per la diagnosi e l'intervento clinico.