Store:Conica

Rappresentazione cinematica attraverso una conica

Per rappresentare in modo più dettagliato e formale la forma ellittica dei tracciati dei denti dovuti al moto rototraslazionale dei condili, possiamo sovrapporre una conica (ellisse) a più punti. Questo ci permetterà di evidenziare il contributo dei movimenti dei condili laterotrusivo e mediotrusivo, nonché delle distanze occlusali da essi, nella generazione di tali tracciati pseudoellittici.

Consideriamo ad esempio il tracciato del molare ipsilaterale durante la laterotrusione. Supponiamo di avere le coordinate di 5 punti distinti su questo tracciato: $(x_{1},y_{1}),(x_{2},y_{2}),(x_{3},y_{3}),(x_{4},y_{4}),(x_{5},y_{5})$.

L'equazione generale di un'ellisse centrata nell'origine è data da:

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1$

Dove $a$ e $b$ sono rispettivamente i semiassi maggiore e minore dell'ellisse.

Per determinare i valori di $a$ e $b$ che meglio approssimano i 5 punti dati, possiamo utilizzare il metodo dei minimi quadrati. L'obiettivo è minimizzare la somma dei quadrati delle distanze dei punti dall'ellisse.

Definiamo la funzione di costo:

$J(a,b)=\sum _{i=1}^{5}\left[\left({\frac {x_{i}^{2}}{a^{2}}}+{\frac {y_{i}^{2}}{b^{2}}}-1\right)^{2}\right]$

Minimizzando $J(a,b)$ rispetto a $a$ e $b$, otteniamo le stime ottimali dei semiassi $a$ e $b$ che approssimano al meglio i punti dati.

Questa ellisse ottimizzata rappresenterà il tracciato pseudoellittico del molare ipsilaterale, influenzato dai movimenti rototraslazionali dei condili laterotrusivo e mediotrusivo, nonché dalle distanze occlusali da essi.

I semiassi $a$ e $b$ dell'ellisse saranno determinati dai pesi relativi dei contributi dei condili e delle distanze occlusali. Ad esempio, un valore di $a$ maggiore potrebbe indicare un'influenza più significativa del condilo laterotrusivo, mentre un valore di $b$ più piccolo potrebbe suggerire un'influenza minore del condilo mediotrusivo o delle distanze occlusali.

Questo approccio può essere applicato anche ai tracciati degli incisivi e dei molari controlaterali, sovrapponendo ellissi ottimizzate ai rispettivi punti per ottenere una rappresentazione formale dei loro tracciati pseudoellittici.

In questo modo, l'analisi matematica dei tracciati dei denti durante la masticazione può essere arricchita con una rappresentazione visiva più dettagliata e quantitativa, permettendo di studiare in modo più approfondito il contributo dei diversi fattori cinematici, come i movimenti dei condili e le distanze occlusali, nella generazione di tali tracciati complessi.

La scelta della conica a 5 punti

La scelta di una conica a 5 punti rappresenta un approccio matematico e geometrico efficace per modellare i tracciati articolari reali rispetto a un'ellisse ideale.

Definizione della conica

Una conica è una curva definita in geometria analitica come il luogo dei punti che soddisfano un'equazione quadratica generale:$Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0$

Dove:

• $A,B,C,D,E,F$ sono coefficienti reali determinati dai punti dati.

La forma della conica (ellisse, parabola o iperbole) dipende dal discriminante:

• Ellisse se $B^{2}-4AC<0$
• Parabola se $B^{2}-4AC=0$
• Iperbole se $B^{2}-4AC>0$

Perché 5 punti?

Una conica è univocamente determinata da 5 punti distinti e non allineati. Questo significa che se conosci 5 punti sperimentali, puoi ricostruire una sola conica che passa per quei punti.

• Univocità: La conica è unica per 5 punti non allineati.
• Adattabilità: Si adatta meglio ai dati sperimentali rispetto a un'ellisse ideale.
• Flessibilità: Modella tracciati complessi, asimmetrici o irregolari, tipici della cinematica mandibolare.

Costruzione delle coniche specifiche

Abbiamo costruito coniche specifiche per diverse aree della traiettoria mandibolare e, comunque, a secondo di cosa si vuole analizzare l'ordine dei punti prescelti può essere cambiato:

Conica del molare laterotrusivo

La conica è stata costruita utilizzando 5 punti chiave lungo il tracciato sperimentale del molare laterotrusivo

• $P_{1}=(68.3,-50.9)$
• $P_{2}=(58.3,-50.9)$
• $P_{3}=(345.2,-844.5)$
• $P_{4}=(255.7,-816)$
• $P_{5}=(509.6,-1139.9)$

Conica dell'incisivo

La conica è stata determinata utilizzando punti significativi lungo la traiettoria reale dello '<<<Incisivo':

• $P_{1}=(509.6,-1139.9)$
• $P_{2}=(631.5,-1151.8)$
• $P_{3}=(68.3,-50.9)$
• $P_{4}=(58.3,-50.9)$
• $P_{5}=(910.7,-856.2)$

Conica del molare mediotrusivo

La conica è stata generata per il 'molare mediotrusivo' usando i seguenti punti chiave:

$P_{1}=(910.7,-856.2)$

• $P_{2}=(818.8,-855.1)$
• $P_{3}=(68.3,-50.9)$
• $P_{4}=(58.3,-50.9)$
• $P_{5}=(345.2,-844.5)$

Costruzione della conica unificata

Per ottenere una visione complessiva (Fig.7b), si è calcolato una 'conica unificata' a partire dalle coniche specifiche. Questa conica è stata costruita mediando i coefficienti delle coniche delle diverse aree:

${\text{Coefficienti Conica Unificata}}={\frac {{\text{Coeff}}_{\text{molare laterotrusivo}}+{\text{Coeff}}_{\text{incisale}}+{\text{Coeff}}_{\text{molare mediotrusivo}}+{\text{Coeff}}_{\text{condilo mediotrusivo}}}{4}}$

L'equazione risultante è:

$Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0$

(dove i coefficienti verranno calcolati sulla base dei punti definitivi).

Figura 7b: Rappresentazione della conica passante per 5 punti strategicamente scelti come descritto nel testo. Notare la discrepanza tra i vettori ed il passaggio della conica che indica il diverso condizionamento della componente traslatoria da quella rotatoria. Effetto che si nota maggiormente sul molare mediotrusivo.

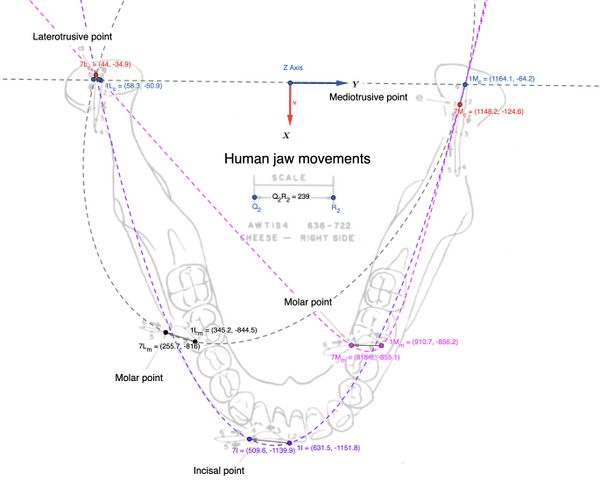
Applicazione della conica per individuare punti cinematici

Utilizzando la conica del molare laterotrusivo, è possibile 'prevedere il punto $7L_{c}$ (condilo laterotrusivo) conoscendo due punti di riferimento (es. punto iniziale e finale sul tracciato molare). Questo approccio permette di determinare con precisione dove cade il punto condilare laterotrusivo sulla conica e utilizzare la conica come strumento per analizzare deviazioni e adattamenti nei tracciati mandibolari reali.