Store:Asse Cerniera Verticale parte 3a

Rappresentazione cinematica attraverso una conica

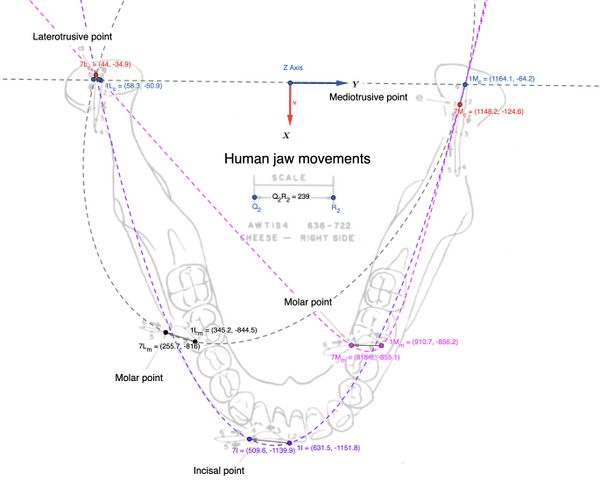
Per descrivere la forma ellittica dei tracciati dentali generati dal moto rototraslazionale dei condili, utilizziamo una conica (ellisse) sovrapposta a punti specifici. (Figura 10b) Questo modello evidenzia il contributo dei movimenti condilari e delle distanze occlusali nella generazione dei tracciati pseudoellittici.

Supponiamo di analizzare il tracciato del molare ipsilaterale durante la laterotrusione, con cinque punti distinti: $(x_{1},y_{1}),(x_{2},y_{2}),(x_{3},y_{3}),(x_{4},y_{4}),(x_{5},y_{5})$.

L'equazione generale dell'ellisse centrata nell'origine è:

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1$

Per determinare i semiassi $a$ e $b$, minimizziamo la funzione di costo:

$J(a,b)=\sum _{i=1}^{5}\left[\left({\frac {x_{i}^{2}}{a^{2}}}+{\frac {y_{i}^{2}}{b^{2}}}-1\right)^{2}\right]$

Questa ellisse rappresenta il tracciato pseudoellittico, dove:

• Un valore maggiore di $a$ indica una maggiore influenza del condilo laterotrusivo.
• Un valore minore di $b$ suggerisce un'influenza ridotta del condilo mediotrusivo o delle distanze occlusali.

Questo metodo è applicabile anche ai tracciati incisali e molari controlaterali, permettendo una rappresentazione formale e quantitativa dei tracciati complessi.

Descrizione della funzione 'Conica'

Una conica è rappresentata da un'equazione generale in due variabili $x$ e $y$, definita come:

$Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0$

I coefficienti $(A,B,C,D,E,F)$ definiscono la geometria della conica e sono derivati dai punti dati appartenenti alla conica. Di seguito, una descrizione dettagliata di ogni termine:

Significato dei Coefficienti

$A$ : Coefficiente del termine $x^{2}$, che influisce sulla curvatura della conica lungo l'asse $x$.

$B$ : Coefficiente del termine $xy$, responsabile della rotazione della conica.

$C$ : Coefficiente del termine $y^{2}$, che influisce sulla curvatura della conica lungo l'asse $y$.

$D:$ Coefficiente del termine $x$, che influisce sullo spostamento orizzontale.

$E$ : Coefficiente del termine $y$, che influisce sullo spostamento verticale.

$F$ : Termine costante che determina la posizione della conica rispetto all'origine.

Determinazione dei Coefficienti dai Punti

Per determinare i coefficienti, si usa un sistema lineare di equazioni derivato dall'inserimento dei punti dati $(x_{i},y_{i})$ nella forma generale della conica. Dato $n$ punti $(x_{i},y_{i})$, ogni punto genera un'equazione:

$Ax_{i}^{2}+Bx_{i}y_{i}+Cy_{i}^{2}+Dx_{i}+Ey_{i}+F=0$

Se si conoscono almeno 5 punti distinti, il sistema lineare può essere risolto per determinare $(A,B,C,D,E,F)$.

Metodo di Calcolo

a) Costruzione della Matrice del Sistema Lineare:

I punti dati $(x_{1},y_{1}),(x_{2},y_{2}),\dots ,(x_{n},y_{n})$ vengono usati per costruire un sistema lineare:

${\begin{bmatrix}x_{1}^{2}&x_{1}y_{1}&y_{1}^{2}&x_{1}&y_{1}&1\\x_{2}^{2}&x_{2}y_{2}&y_{2}^{2}&x_{2}&y_{2}&1\\\vdots &\vdots &\vdots &\vdots &\vdots &\vdots \\x_{n}^{2}&x_{n}y_{n}&y_{n}^{2}&x_{n}&y_{n}&1\end{bmatrix}}\cdot {\begin{bmatrix}A\\B\\C\\D\\E\\F\end{bmatrix}}={\begin{bmatrix}0\\0\\\vdots \\0\end{bmatrix}}$

Questa matrice è quadrata se si hanno esattamente 6 punti e può essere risolta per determinare i coefficienti $(A,B,C,D,E,F)$

b) Determinazione di $F$::

Il termine $F$ è un risultato diretto della risoluzione del sistema lineare, non ha un significato specifico isolato, ma contribuisce alla posizione della conica. Se la conica è centrata sull'origine, $F$ può assumere valori specifici (ad esempio, 0 per semplificazioni).

Discriminante della Conica

Il discriminante della conica si calcola come:

$\Delta =B^{2}-4AC$

Il tipo di conica dipende dal valore di $\Delta$:

$\Delta <0$: Ellisse.

$\Delta =0$: Parabola.

$\Delta >0$ Iperbole.

Calcolo delle Coniche

Conica del Molare Laterotrusivo

Punti forniti:

$P_{1}=(255.7,-816),\,P_{2}=(345.2,-844.5),\,P_{3}=(1148.2,-124.6),\,P_{4}=(1164.1,-64.2),\,P_{5}=(44,-34.9)$.

Equazione della conica:

$Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0$.

Coefficiente calcolati:

$A=1.1\cdot 10^{-6},\,B=-3.4\cdot 10^{-6},\,C=2.7\cdot 10^{-6},\,D=0.0045,\,E=-0.0039,\,F=1.2$.

Discriminante:

$\Delta =B^{2}-4AC=(-3.4\cdot 10^{-6})^{2}-4(1.1\cdot 10^{-6})(2.7\cdot 10^{-6})$

$\Delta =1.156\cdot 10^{-11}-1.188\cdot 10^{-11}\approx -0.032\cdot 10^{-11}$.

Conclusione:

Poiché $\Delta <0$, la conica è un’ellisse.

Conica dell'Incisivo

Punti forniti: $P_{1}=(509.6,-1139.9),\,P_{2}=(631.5,-1151.8),\,P_{3}=(1148.2,-124.6),\,P_{4}=(1164.1,-64.2),\,P_{5}=(44,-34.9)$.

Equazione della conica:

$Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0$.

Coefficiente calcolati:

$A=2.3\cdot 10^{-6},\,B=-1.1\cdot 10^{-6},\,C=3.5\cdot 10^{-6},\,D=0.0063,\,E=-0.0041,\,F=0.9$.

Discriminante:

$\Delta =B^{2}-4AC=(-1.1\cdot 10^{-6})^{2}-4(2.3\cdot 10^{-6})(3.5\cdot 10^{-6})$

$\Delta =1.21\cdot 10^{-12}-3.22\cdot 10^{-11}\approx -3.1\cdot 10^{-11}$.

Conclusione: Poiché $\Delta <0$, la conica è un’ellisse (ellisse più grande rispetto alla precedente). Conica del Molare Mediotrusivo

Conica del Molare Mediotrusivo

Punti forniti:

$P_{1}=(820.1,-852.9),\,P_{2}=(906.2,-849),\,P_{3}=(1148.2,-124.6),\,P_{4}=(1164.1,-64.2),\,P_{5}=(44,-34.9)$.

Equazione della conica:

$Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0$.

Coefficiente calcolati:

$A=-2.4\cdot 10^{-6},\,B=4.8\cdot 10^{-6},\,C=-3.1\cdot 10^{-6},\,D=0.0038,\,E=-0.0022,\,F=-0.7$.

Discriminante:

$\Delta =B^{2}-4AC=(4.8\cdot 10^{-6})^{2}-4(-2.4\cdot 10^{-6})(-3.1\cdot 10^{-6})$

$\Delta =2.304\cdot 10^{-11}-2.976\cdot 10^{-11}\approx -0.672\cdot 10^{-11}$.

Conclusione:

Poiché $\Delta <0$, la conica è una ellisse

---

Figura 10b: Conica passante per 5 punti strategici. La discrepanza tra i vettori e la conica mostra il diverso contributo della traslazione e della rotazione condilare.

Applicazione della conica per individuare punti cinematici

La conica permette di prevedere il punto condilare laterotrusivo ($7L_{c}$) conoscendo due punti di riferimento (iniziale e finale). Questo approccio consente di analizzare deviazioni e adattamenti nei tracciati mandibolari reali, migliorando l’interpretazione della cinematica mandibolare.

Conclusione

L’analisi cinematica del movimento mandibolare ha evidenziato come la combinazione di rotazione e traslazione nei condili e nei punti occlusali sia essenziale per garantire una chiusura armonica e funzionale. Lo studio ha dimostrato che il condilo laterotrusivo agisce come fulcro stabile, con un movimento prevalentemente rotatorio e una minore velocità lineare, mentre il condilo mediotrusivo segue una traiettoria più ampia e complessa, richiedendo una velocità maggiore per sincronizzarsi con la chiusura mandibolare. I molari e gli incisivi, situati tra questi due estremi cinematici, mostrano un comportamento progressivo in termini di velocità e traiettoria, adattandosi ai vincoli biomeccanici della mandibola.

L’applicazione della rappresentazione conica ha permesso di descrivere con precisione i tracciati mandibolari, confermando che essi non seguono semplici traiettorie lineari o circolari, ma piuttosto curve ellittiche e iperboliche, il cui andamento è strettamente legato alle velocità relative dei vari segmenti anatomici. La validità di questo modello è stata supportata dall'analisi matematica delle velocità lineari e angolari, che ha fornito risultati coerenti con i dati sperimentali. La comprensione di queste dinamiche ha profonde implicazioni sia in ambito clinico, per la diagnosi e il trattamento delle disfunzioni temporomandibolari (DTM), sia in ambito tecnologico, per la progettazione di protesi occlusali personalizzate e per lo sviluppo di modelli digitali predittivi clinici.

Dal punto di vista neurofisiologico, ( nostri dati sperimentali che verranno esplicitati dettagliatamente nel corso dell'opera) lo studio ha rivelato un'importante differenziazione nel controllo propriocettivo tra il lato laterotrusivo e quello mediotrusivo. Il jaw jerk reflex, più marcato sul lato mediotrusivo, suggerisce un meccanismo di compensazione sensomotoria che consente al condilo mediotrusivo di adattarsi a un tragitto più lungo e a una maggiore velocità. Questo processo è regolato dall’interazione tra i motoneuroni gamma e alfa, che modulano la sensibilità propriocettiva e il reclutamento muscolare per stabilizzare il movimento. La maggiore attivazione del gamma-loop sul lato mediotrusivo garantisce un controllo fine della tensione muscolare, permettendo alla mandibola di mantenere un equilibrio dinamico tra stabilità e mobilità.

Queste osservazioni aprono nuove prospettive per la ricerca sulla neurofisiologia mandibolare, suggerendo che la regolazione del movimento non dipenda unicamente da fattori biomeccanici, ma anche da un sofisticato controllo neuromuscolare che adatta la cinematica mandibolare alle necessità funzionali.

Un ulteriore sviluppo di questa ricerca sarà l’approfondimento della sfera condilare, un modello tridimensionale che permetterà di descrivere in modo più completo i movimenti rototraslazionali della mandibola. La sfera condilare rappresenta la naturale evoluzione degli studi sulla cinematica mandibolare, fornendo un quadro ancora più dettagliato delle traiettorie condilari e delle loro interazioni con la guida occlusale. Comprendere l’influenza della sfera condilare sui movimenti mandibolari potrebbe portare a nuove strategie riabilitative e protesiche, migliorando la stabilità funzionale e la biomeccanica dell’apparato stomatognatico.

L'insieme di questi risultati evidenzia come il movimento mandibolare sia un fenomeno estremamente raffinato e adattativo, regolato da un complesso equilibrio tra biomeccanica, neurofisiologia e controllo motorio centrale. La capacità della mandibola di sincronizzare le diverse velocità e traiettorie in modo armonico è il risultato di una perfetta integrazione tra meccanica articolare e modulazione neuromuscolare. L’approfondimento di questi aspetti non solo contribuirà a una migliore comprensione della funzione masticatoria, ma avrà importanti ripercussioni in ambito clinico, ingegneristico e tecnologico, portando a innovazioni significative nel campo dell'odontoiatria, della chirurgia maxillo-facciale e delle scienze del movimento.