Store:Store:46laterotrusivo

Go to top

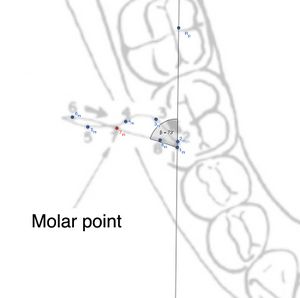
Molare laterotrusivo

Il testo descrive un'analisi dettagliata dei movimenti articolari del molare ipsilaterale al condilo laterotrusivo (Figura 3 e tabella 2)e coinvolge vari punti nello spazio 2D per calcolare distanze e angoli utilizzando la trigonometria vettoriale.

Figura 3: Rappresentazione delle distanze tra punti nel molare ipsilaterale alla laterotrusione

Tabella 2
Point	Distance (pixels)	Distance (mm)	Direzione in X (antero-posteriore)	Direzione in Y (latero-mediale)
2	8.74	0.874 mm	Indietro	Laterale
3	54.42	5.442 mm	Indietro	Laterale
4	84.64	8.464 mm	Indietro	Laterale
5	134.48	13.448 mm	Indietro	Laterale
6	160.59	16.059 mm	Indietro	Laterale
7*	91.99	9.199 mm	Indietro	Laterale
8	27.65	2.77 mm	Indietro	Laterale
Rappresentazione delle distanze e dell'angolo formato tra i puntimarcati nel ciclo masticatorio riferiti al punto 1 di massima intercuspidazione. IL punto 7* è il punto considerato per lo specifico calcolo del molare laterotrusivo

Il formalismo matematico Nel contesto della nostra analisi, abbiamo tre punti nello spazio 2D che ci interessano: Coordinate $P1_{m}$ del punto 1 del molare ipsilaterale al condilo latorotrusivo: $(345.2,-844.5)$ *Coordinate $P7_{m}$ del punto 7 del molare ipsilaterale al condilo latorotrusivo: $(255.7,-816)$ *Coordinate $H3_{m}$ del punto di riferimento del condilo mediotrusivo: $(347.7,-682.7)$ Questi punti rappresentano tre posizioni specifiche all'interno di un sistema articolare che stiamo studiando, con l'obiettivo di calcolare l'angolo tra il segmento che unisce i punti $P1_{m}$ e $P7_{m}$ , e il segmento che unisce i punti $P1_{m}$ e $H3_{m}$ . Questo tipo di analisi è comune nella modellazione di movimenti articolari per comprendere come si muovono i segmenti di un sistema rispetto a un punto di riferimento, come nel caso di un sistema masticatorio.Iter matematico per il calcolo dell'angolo L'angolo tra due segmenti può essere calcolato utilizzando la **trigonometria vettoriale** e, in particolare, il **prodotto scalare**. Questo metodo è utile quando vogliamo determinare la relazione angolare tra due movimenti distinti nello spazio. Definizione dei vettori *Il vettore tra il punto $P1_{m}$ e il punto $P7_{m}$ : ${\vec {AB}}=P7_{m}-P1_{m}=(255.7,-816)-(345.2,-844.5)=(-89.5,28.5)$ *Il vettore tra il punto $P1_{m}$ e il punto $H3_{m}$ : ${\vec {AC}}={\vec {H_{3}}}-{\vec {P_{1}}}=(347.7,-682.7)-(345.2,-844.5)=(2.5,161.8)$ Innanzitutto, dobbiamo calcolare i vettori che rappresentano i segmenti tra i punti: Prodotto scalareSostituendo i valori calcolati: ${\vec {AB}}\cdot {\vec {AC}}=(-89.5)\cdot (2.5)+(28.5)\cdot (161.8)=-223.75+4601.3=4377.55$ Il **prodotto scalare** tra due vettori ${\vec {AB}}$ e ${\vec {AC}}$ è dato dalla formula: ${\vec {AB}}\cdot {\vec {AC}}=AB_{x}\cdot AC_{x}+AB_{y}\cdot AC_{y}$ Calcolo delle norme $|{\vec {AB}}|={\sqrt {AB_{x}^{2}+AB_{y}^{2}}}={\sqrt {(-89.5)^{2}+(28.5)^{2}}}={\sqrt {8010.25+812.25}}={\sqrt {8822.5}}\approx 93.96$ $|{\vec {AC}}|={\sqrt {AC_{x}^{2}+AC_{y}^{2}}}={\sqrt {(2.5)^{2}+(161.8)^{2}}}={\sqrt {6.25+26178.44}}={\sqrt {26184.69}}\approx 161.78$ . Le norme (lunghezze) dei due vettori sono calcolate con la formula della lunghezza del vettore Calcolo dell'angolo $\cos(\theta )={\frac {{\vec {AB}}\cdot {\vec {AC}}}{|{\vec {AB}}|\cdot |{\vec {AC}}|}}$ Sostituendo i valori: $\cos(\theta )={\frac {4377.55}{93.96\cdot 161.78}}={\frac {4377.55}{15193.68}}\approx 0.288$ Ora possiamo usare la formula per il coseno dell'angolo tra i due vettori: Infine, l'angolo $\theta$ è calcolato tramite la funzione arcoseno: $\theta =\arccos(0.288)\approx 73.32^{\circ }$ Motivo dell'analisi L'obiettivo dell'analisi è determinare l'angolo tra due movimenti all'interno di un sistema articolare, in particolare nell'area di studio della cinematica masticatoria. può essere riassunto come segue:

Distanze calcolate tra i punti

Tabella delle distanze: Viene fornita una tabella che mostra la distanza tra vari punti, espressa in pixel e convertita in millimetri, con indicazione della direzione sia in senso antero-posteriore ( $X$ ) che latero-mediale ( $Y$ ). Tutti i movimenti del molare sono stati riportati come "Indietro" e "Laterale".

Analisi matematica dei punti

Punti coinvolti:
- Il punto 1 ( $P_{1}$ ) del molare ipsilaterale al condilo laterotrusivo si trova a coordinate ( $345.2,-844.5$ ).
- Il punto 7 ( $P_{7}$ ) dello stesso molare si trova a ( $255.7,-816$ ).
- Il punto di riferimento $R_{p}$ del condilo mediotrusivo si trova a ( $347.7,-682.7$ ).

Obiettivo: L'analisi si propone di calcolare l'angolo tra il segmento che collega i punti $P_{1}$ e $P_{7}$ e il segmento che collega i punti $P_{1}$ e $R_{p}$ .

Calcolo dei vettori:Sono stati definiti due vettori, uno tra i punti $P_{1}$ e $P_{7}$ e uno tra i punti $P_{1}$ e $R_{p}$ .

Prodotto scalare: Utilizzando il prodotto scalare tra i vettori, si è ottenuto un valore di $4377.55.$

Calcolo delle norme: Le lunghezze dei vettori risultano essere circa $93.96$ per ${\vec {AB}}$ e $161.78$ per ${\vec {AC}}$ .

Angolo: Il coseno dell'angolo è stato calcolato come $0.288$ , con l'angolo risultante approssimativamente pari a $73.32^{\circ }$ .