Masticationpedia

Dynamique physiologique dans les maladies démyélinisantes : démêler les relations complexes grâce à la modélisation informatique

Page Discussion
Revision as of 15:31, 3 May 2023 by Luca (talk | contribs)
Go to top
Other languages:  

English · Italiano · Français · Deutsch · Español · 

Free resource
Title Dynamique physiologique dans les maladies démyélinisantes : démêler les relations complexes grâce à la modélisation informatique
Authors Jay S. Coggan · Stefan Bittner · Klaus M. Stiefel · Sven G. Meuth · Steven A. Prescott
Source Document
Date 2021
Journal Int J Mol Sci.
DOI 10.3390/ijms160921215
PUBMED https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4613250/#!po=53.5714
PDF copy
Crystal Clear mimetype pdf.png
License CC BY
This resource has been identified as a Free Scientific Resource, this is why Masticationpedia presents it here as a mean of gratitude toward the Authors, with appreciation for their choice of releasing it open to anyone's access

This is free scientific content. It has been released with a free license, this is why we can present it here now, for your convenience. Free knowledge, free access to scientific knowledge is a right of yours; it helps Science to grow, it helps you to have access to Science

This content was relased with a 'CC BY' license.
You might perhaps wish to thank the Author/s

Dynamique physiologique dans les maladies démyélinisantes : démêler les relations complexes grâce à la modélisation informatique

Open Access logo green alt2.svg
Free resource by Jay S. Coggan  · Stefan Bittner · Klaus M. Stiefel  · Sven G. Meuth · Steven A. Prescott



Physiological Dynamics in Demyelinating Diseases: Unraveling Complex Relationships through Computer Modeling

Jay S. Coggan, Stefan Bittner, [...], and Steven A. Prescott

Additional article information

Abstrait

Malgré des recherches intenses, peu de traitements sont disponibles pour la plupart des troubles neurologiques. Les maladies démyélinisantes ne font pas exception. Ce n'est peut-être pas surprenant compte tenu de la nature multifactorielle de ces maladies, qui impliquent des interactions complexes entre les cellules du système immunitaire, la glie et les neurones. Dans le cas de la sclérose en plaques, par exemple, il n'y a pas d'unanimité parmi les chercheurs sur la cause ou même sur le système ou le type de cellule qui pourrait être le point zéro. Cette situation empêche le développement et l'application stratégique de thérapies basées sur les mécanismes. Nous discuterons de la manière dont la modélisation computationnelle appliquée à des questions à différents niveaux biologiques peut aider à relier des observations disparates et à déchiffrer des mécanismes complexes dont les solutions ne se prêtent pas au simple réductionnisme. En faisant des prédictions vérifiables et en révélant des lacunes critiques dans les connaissances existantes, ces modèles peuvent aider à orienter la recherche et fourniront un cadre rigoureux dans lequel intégrer de nouvelles données au fur et à mesure de leur collecte. De nos jours, les données ne manquent pas ; le défi est de donner un sens à tout cela. À cet égard, la modélisation informatique est un outil inestimable qui pourrait, à terme, transformer la façon dont nous comprenons, diagnostiquons et traitons les maladies démyélinisantes.

Mots-clés : myéline, démyélinisation, sclérose en plaques, maladie neurodégénérative, modèle informatique, découverte de médicaments



Introduction

Les systèmes nerveux des vertébrés sont souvent divisés en matière grise et blanche en fonction de leur apparence et des rôles fonctionnels correspondants. Alors que la matière grise se compose en grande partie de corps cellulaires et de dendrites, la matière blanche contient principalement des axones et tire son nom des feuilles de membrane lipidique appelées myéline qui sont étroitement enroulées autour de ces axones..[1] La myéline provient de différentes classes de cellules gliales appelées oligodendrocytes dans le système nerveux central (SNC) et cellules de Schwann dans le système nerveux périphérique (SNP).

L'isolation électrique fournie par les feuilles de myéline améliore la fonction axonale en augmentant à la fois l'efficacité énergétique et la vitesse de conduction des potentiels d'action (PA). Ces deux fonctions peuvent avoir changé d'importance relative au cours de l'évolution.[2] La myéline est apparue pour la première fois à l'Ordovicien (485 à 443 ma, soit des millions d'années avant le présent) après la scission des ancêtres de la lamproie et de la myxine du reste des lignées de vertébrés.[3] Avec quelques exceptions intéressantes,[4][5]la myéline ou des structures analogues se trouvent chez tous les vertébrés et sont essentielles au bon fonctionnement de leur système nerveux. Le temps approximatif de l'évolution de la myéline peut être déduit du temps connu de divergence entre les accords sans (agnatha) et avec (tous les autres vertébrés) myéline.

L'enveloppe de myéline est interrompue par des tronçons non myélinisés régulièrement espacés connus sous le nom de nœuds de Ranvier. La myéline accélère la conduction en limitant le flux de charge transmembranaire à travers les canaux ioniques situés dans les nœuds. Dans les soi-disant entre-nœuds, le courant circule le long de l'axone avec peu de passage à travers la membrane cellulaire isolée. Le PA est régénéré à chaque nœud où la densité des canaux sodiques et potassiques voltage-dépendants est très élevée. Ce processus est appelé "conduction saltatoire" car le point d'accès semble sauter d'un nœud à l'autre. Les perturbations de ce système de communication rapide peuvent être associées à un éventail de dysfonctionnements du système nerveux.[6]

À plusieurs égards, les axones semblent fonctionner à des limites physiques. Un exemple intéressant est que la taille des axones semble être contrainte par le bruit thermique intrinsèque aux protéines des canaux ioniques ; tout axone plus fin que 0,1 μm serait inutile pour le transfert d'informations en raison de ses niveaux de bruit élevés.[7] Curieusement, 0,1 μm est également à peu près le plus petit diamètre d'axone observé dans les systèmes nerveux [7]. Ceci et des découvertes similaires suggèrent que les axones et leurs sous-structures sont des dispositifs biologiques finement réglés, mais que le réglage peut évidemment être perturbé dans des conditions pathologiques..[8]

La démyélinisation met en mouvement des changements fonctionnels qui sont importants pour les caractéristiques cliniques mais qui ne sont pas facilement expliqués par des changements immunologiques ou radiologiques. L'emplacement d'une plaque prédit quel système sera affecté (moteur vs sensoriel, visuel vs tactile) mais pas comment il sera affecté. Cela met en évidence l'importance d'évaluer la fonction (en plus de la structure) et comment elle change après la démyélinisation. Après avoir présenté les maladies démyélinisantes, nous discuterons de la manière dont les manifestations cliniques de ces maladies reflètent divers changements pathologiques dans la fonction des axones. Nous soutiendrons que comprendre ces changements et tirer pleinement parti de cette compréhension à des fins diagnostiques et thérapeutiques peut bénéficier énormément de la modélisation informatique.

Maladies démyélinisantes

Figure 1 : Affections démyélinisantes du système nerveux périphérique (SNP). (A) Polyneuropathies démyélinisantes primaires et (B) Polyneuropathies avec lésions axonales. Abréviations : CMT 1, 2 et 4 : maladie de Charcot-Marie-Tooth ; CMTX : maladie de Charcot-Marie-Tooth liée à l'X ; HNPP : neuropathie héréditaire avec risque de paralysie de pression ; AIDP : polyneuropathie démyélinisante inflammatoire aiguë ; SGB : syndrome de Guillain-Barré. PIDC : polyneuropathie démyélinisante inflammatoire chronique ; MGUS : gammapathie monoclonale de signification indéterminée ; POEMS : polyneuropathie, organomégalie, endocrinopathie ou œdème de la protéine M et anomalies cutanées ; HSAN I–IV : neuropathie sensorielle et autonome héréditaire.

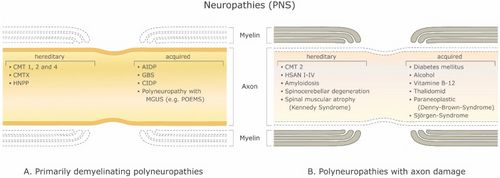
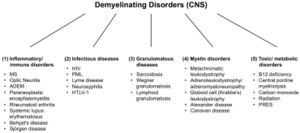
Il existe un grand nombre de maladies démyélinisantes affectant à la fois le SNP (Figure 1) et le SNC (Figure 2). Les étiologies sont hétérogènes, allant des troubles génétiques aux mécanismes métaboliques, infectieux ou auto-immuns. La sclérose en plaques (SEP) est la plus répandue de ces maladies, avec environ 3 millions de patients dans le monde. Sa cause sous-jacente est incertaine, mais on pense qu'elle implique une prédisposition génétique aux agents environnementaux[9][10]et peut impliquer des composants immunologiques, de réactivité aux traumatismes, biophysiques, génétiques et/ou métaboliques.[10] Les symptômes et les lésions doivent être multiples dans le temps et dans l'espace. Autrement dit, il doit y avoir plusieurs épisodes dans le temps, impliquant des parties déconnectées du système nerveux central. Il n'est pas clair si la démyélinisation inflammatoire est un événement primaire ou secondaire dans le processus de la maladie.[9][11][12]La plupart des traitements ciblent le système immunitaire ou la barrière hémato-encéphalique, mais la gestion des symptômes neurologiques par la modulation de l'excitabilité axonale joue également un rôle important (voir ci-dessous).

Figure 2 : Troubles démyélinisants du système nerveux central (SNC). Abréviations : SEP : sclérose en plaques ; ADEM : encéphalomyélite aiguë disséminée ; VIH : virus de l'immunodéficience humaine ; LMP : leucoencéphalopathie multifocale progressive ; HTLV-1 : virus T-lymphotrope humain 1 ; PRES : syndrome d'encéphalopathie postérieure réversible.

Évaluation clinique de la sclérose en plaques

Les symptômes sont divers et peuvent survenir dans toutes les combinaisons au sein d'un même patient. Le diagnostic exige qu'il y ait plusieurs lésions et épisodes symptomatiques au fil du temps, impliquant des parties déconnectées du SNC. De plus, les symptômes ont tendance à être peu corrélés aux mesures radiologiques. Dans la grande majorité des cas, les caractéristiques cliniques individuelles ne sont pas bien corrélées avec les résultats de l'IRM, en particulier pour les lésions cérébrales.[13][14][15]Cette dissociation clinico-radiologique demande une meilleure compréhension théorique des symptômes de démyélinisation et des changements biophysiques sous-jacents qui les accompagnent, ce qui soulève bien sûr la question de ce qu'il advient exactement des axones affectés.

Les symptômes sont souvent intermittents et peuvent inclure à la fois une perte de fonction (symptômes négatifs tels qu'engourdissement, faiblesse musculaire, picotements, cécité, incontinence, perte de la fonction sexuelle, perte d'équilibre, troubles de l'élocution, constipation, fatigue invalidante, dépression, dysfonctionnement cognitif , incapacité à avaler, perturbation de la marche et perte de contrôle de la respiration) et gain de fonction (symptômes positifs tels que spasmes, spasticité, crampes, douleur, vision floue ou double, urgence ou hésitation urinaire, nausées, entre autres).[16]Les critères diagnostiques différentiels précoces incluent le signe de Lhermitte (sensations liées à la flexion du cou) et le phénomène d'Uhthoff (aggravation des symptômes liée à la température). Le diagnostic différentiel de la SEP suit de près les critères de McDonald.[17]

Dans les études diagnostiques humaines des potentiels évoqués visuels, sensoriels ou moteurs (VEP, SEP, MEP), seule la latence ou la vitesse de conduction peut être mesurée avec précision (avec des variations d'environ 30 % à 40 % entre les différents laboratoires). Mais ces mesures donnent peu d'indices sur les mécanismes sous-jacents qui impliquent un ralentissement ou un blocage de la conduction, ou des facteurs morphologiques ou fonctionnels tels que la ramification, la démyélinisation, la remyélinisation, l'effilement axonal (diminution de la section transversale), l'atténuation ou la repousse, les changements de conduction liés à la température. , ou malpolarisation (hyper ou hypo). Néanmoins, le type de lésion démyélinisante peut fournir des indices sur l'étiologie et donc orienter le traitement ; par exemple, les facteurs génétiques semblent être plus fortement corrélés aux processus pathologiques internodaux et les dysfonctionnements immunologiques provoquent des anomalies paranodales.[18]

Un certain nombre de tests sont couramment utilisés pour évaluer la fonction neurale. En électroneurographie, un bref stimulus électrique est appliqué à un nerf périphérique à une position anatomiquement prédéfinie afin de mesurer la latence et l'amplitude du potentiel d'action composé à un autre endroit le long du nerf. Les résultats doivent être interprétés en combinaison avec les résultats cliniques et les tests (par exemple, l'électromyographie) mais, ce qui est important, différentes maladies présentent différents modèles de changements électroneurographiques. Ceci est important non seulement à des fins de diagnostic, mais peut également indiquer des changements pathologiques spécifiques dans la fonction axonale qui pourraient, à leur tour, aider à guider le choix de la thérapie (si la pathobiologie axonale était comprise ; voir ci-dessous). À l'aide d'un suivi de seuil, l'excitabilité a été mesurée chez l'homme pour plusieurs maladies démyélinisantes périphériques, notamment la maladie de Charcot-Marie-Tooth de type 1A (CMT1A), la polyneuropathie démyélinisante inflammatoire chronique (PDIC), le syndrome de Guillain-Barré (SGB) et la neuropathie motrice multifocale (MMN). ).[19][20][21][22][23][24][25] The Le défi réside dans l'interprétation de ces observations. À cette fin, le groupe de Stephanova a simulé des degrés progressivement plus élevés de démyélinisation systématique et focale des fibres motrices pour tenter d'expliquer les changements physiologiques observés.[26][27][28][29][30][31] (voir la section Modélisation ci-dessous).

Implication des corps cellulaires

La progression de la SEP récurrente-rémittente (RRMS) à la SEP progressive secondaire (SPMS) est associée à une plus grande implication de la pathologie de la matière grise, bien que l'implication axonale/de la matière grise puisse déjà être observée dans les premiers stades de la maladie.[32][33][34][35] Les dommages à la matière grise sont considérés comme le mécanisme sous-jacent de la progression de la maladie et de l'invalidité permanente chez les patients atteints de SEP, et sont mesurés par la perte de la fraction parenchymateuse cérébrale ou du volume cérébral par IRM ou cliniquement par la progression sur l'échelle élargie d'état d'invalidité (EDSS).[36]La transition de RRMS à SPMS est inquiétante en raison du manque de traitements pour lutter contre la détérioration physique et cognitive exacerbée à laquelle la plupart des patients SPMS sont confrontés.[9][37]

Traitement

Les principales interventions dans la SEP consistent à moduler la réponse immunitaire avec, par exemple, la méthy-prednisolone, l'interféron bêta, l'acétate de glatiramère ou le fingolimod, ou en empêchant les cellules inflammatoires de traverser la BHE (anticorps monoclonaux, par exemple Tysabri (anti α4-intégrine, Natalizumab )). Très récemment, les deux premiers agents oraux (fumarate et tériflunomide) ainsi que l'anticorps anti-CD52 Natalizumab ont été approuvés pour le traitement de la SEP-RR, qui peuvent être traités avec succès par des thérapies de première ligne comme les interférons, l'acétate de glatiramère ou le fingolimod, ou par thérapeutiques de seconde intention, mais les formes progressives (PPMS, SPMS) représentent encore un besoin biomédical non satisfait.[38]Les antinéoplasiques sont utilisés dans les cas extrêmement avancés ou difficiles.[39]

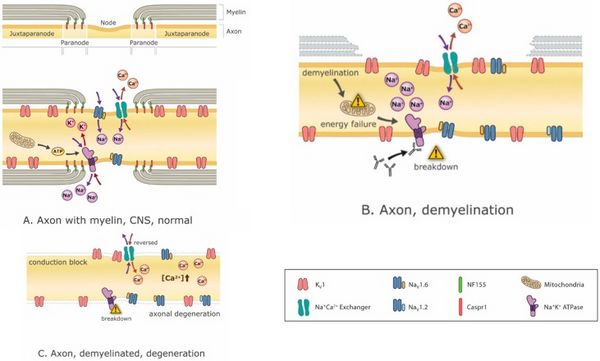
Les médicaments modificateurs de la maladie sont essentiels pour arrêter ou au moins atténuer le processus de démyélinisation, mais il est également essentiel de gérer les symptômes résultant de la démyélinisation qui s'est déjà produite. La modulation des canaux ioniques est de plus en plus prometteuse avec l'avènement de nouveaux bloqueurs de canaux ioniques comme l'Ampyra (blocage des canaux K).[40][41] Le blocage des canaux potassiques vise à améliorer l'excitabilité des axones. Le problème est que de telles interventions, bien qu'efficaces pour traiter les symptômes négatifs et restaurer la fonction, ont tendance à exacerber les symptômes positifs..[42]À l'inverse, le traitement des symptômes positifs tels que les spasmes avec des antiépileptiques comme la carbamazépine, par exemple, peut exacerber les symptômes négatifs.[43] En fait, le blocage des canaux Na+ réduit non seulement les symptômes positifs, mais peut également être neuroprotecteur (car l'accumulation de Na+ provoque des mécanismes d'échange Na+/Ca2+ pour charger les neurones avec Ca2+, qui est excitotoxique)[44] (Figure 3) mais ces avantages se font au détriment des symptômes négatifs. Par conséquent, et en particulier chez un patient présentant un mélange de symptômes positifs et négatifs, les options de traitement sont limitées.

Mécanismes de la neurodégénérescence liée à la démyélinisation. La démyélinisation peut entraîner progressivement des déséquilibres ioniques, une crise énergétique, un blocage de la conduction et éventuellement une neurodégénérescence. (A) un nœud normal de Ranvier avec des régions juxtaparanodales, paranodales et nodales intactes, représentant ions circulant à travers leurs canaux respectifs avec des mitochondries fournissant l'ATP pour l'énergie dépendante ases qui rétablissent les gradients ioniques appauvris par le flux ionique à travers les canaux. De nombreux canaux ioniques différents sont présents dans l'axone, mais seul un petit sous-ensemble est représenté ici ; (B) la démyélinisation partielle entraîne la dispersion des canaux ioniques nodaux, une insuffisance énergétique et des déséquilibres des gradients ioniques ; (C) une démyélinisation complète peut entraîner un blocage de la conduction et une dégénérescence axonale en raison de l'accumulation de qui résulte de la crise énergétique et de la perturbation des équilibres ioniques. Abbreviations :: canal potassique de type 1 et : : canaux sodiques types 1.6 et 1.2 ; Echangeur : pompe d'échange ; ase : dépendant de l'ATP (énergie) pompe d'échange ; CASPR1 : protéine 1 associée à la contactine (molécule d'interaction entre cellule myélinisante et axone) ;; : neurofascine 155 (molécule d'interaction prédominante entre la myéline et l'axone au niveau de la jonction axo-gliale paranodale)..


La discussion ci-dessus soulève le point important que bien que beaucoup de bruit ait été fait sur les mécanismes immunitaires, leur lien avec les changements cliniques est largement corrélationnel. Il faut considérer les effets intermédiaires sur la fonction axonale, à savoir les modifications primaires et secondaires (compensatoires) de l'excitabilité axonale, afin d'apprécier comment la fonction neurologique est altérée. Ces changements ne sont pas des conséquences simples et directes de la démyélinisation, mais suggèrent plutôt que la physiologie axonale elle-même change en réponse à la démyélinisation. Certains de ces changements sont adaptatifs tandis que d'autres sont inadaptés, ou peut-être que les changements adaptatifs peuvent devenir inadaptés à mesure que la situation (état de la myélinisation) évolue. Si des changements dans la physiologie axonale dictent la manifestation de divers symptômes, la gestion des symptômes reposera en grande partie sur des traitements visant à manipuler la physiologie axonale. Le développement stratégique de tels traitements nécessite une compréhension approfondie et mécaniste de l'excitabilité axonale et de sa régulation.

Pathobiologie des axones

Changements structurels et moléculaires

Les axones sont profondément affectés par la démyélinisation. La morphologie de l'axone devient irrégulière ou enflée, souvent avec un aspect perlé. Une accumulation focale de protéines (par transport axonal rapide) est également observée. Dans les plaques actives chroniques, une perte axonale de 20 % à 80 % est apparente dans la substance blanche péri-plaque et la substance blanche distante normale.[45] Dans les plaques actives précoces et chroniques actives, on pense que les dommages sont causés par des facteurs inflammatoires et immunitaires libérés lors de la démyélinisation inflammatoire aiguë. Les médiateurs proposés comprennent les protéases, les cytokines, les excitotoxines et les radicaux libres. Les antigènes neuronaux sont les cibles d'une réaction immunitaire conduisant à une inflammation du SNC. D'autres facteurs causant un dysfonctionnement axonal ou la mort comprennent un manque de soutien trophique de la myéline et des oligodendrocytes, des dommages causés par des facteurs immunitaires solubles ou cellulaires encore présents dans la plaque inactive et une défaillance mitochondriale chronique dans le cadre de demandes énergétiques accrues.[46] Un rôle critique des oligodendrocytes et des cellules de Schwann dans la survie des axones a également été attribué aux peroxysomes, au métabolisme des lipides et à la détoxification des espèces réactives de l'oxygène (ROS)..[47]

La remyélinisation est souvent observée sous forme de plaques d'ombre formées par le recrutement de précurseurs d'oligodendrocytes indifférenciés qui migrent vers et entourent les lésions permettant de fines couches de remyélinisation.[48]Ce processus se produit principalement dans les plaques actives aiguës, mais aussi dans les phases chroniques. Cette observation a déclenché le développement d'un nouvel anticorps monoclonal dirigé contre LINGO-1 (Anti-LINGO-1). La liaison de LINGO-1 aux récepteurs Nogo empêche les processus de remyélinisation dans le SNC ; l'inhibition de cette interaction permet ainsi une remyélinisation significative chez les animaux atteints d'encéphalomyélite auto-immune expérimentale.[49]

Au cours du processus de la maladie, les lymphocytes et les macrophages autoréactifs peuvent traverser la barrière hémato-encéphalique et s'accumuler dans le cerveau et la moelle épinière.[50] Les lymphocytes régulateurs (Tregs) ne parviennent pas à supprimer les cellules effectrices, principalement les cellules CD8+ cytotoxiques.[51] La libération de cytokines pro-inflammatoires recrute des microglies naïves, qui entrent en contact avec une unité oligodendrocyte-myéline par des interactions avec les récepteurs Fc et du complément. Un signal cytotoxique déclenchant la mort est ensuite transmis par le facteur de nécrose tumorale α (TNFα) lié à la surface.[52]Cela se produit de concert avec des dommages axonaux importants.[10]

Lucchinetti el al.[46]ont proposé quatre immunopatterns distincts de formation de plaque trouvés chez des patients à différents stades de la maladie. Les plaques de type I et II sont dominées par l'inflammation des lymphocytes T et des macrophages et on pense qu'elles imitent respectivement les modèles d'encéphalomyélite auto-immune à cellules T ou à cellules T plus anticorps. La perte de myéline dans les plaques de type I peut être causée par des facteurs toxiques libérés par les macrophages activés, alors que les dépôts d'IgG et de complément suggèrent un rôle des anticorps dans les plaques de type II. En revanche, les schémas III et IV montrent une grande dystrophie oligodendrocytaire. On pense que le motif III est lié à des lésions induites par l'hypoxie qui sont entraînées par des défauts de la fonction mitochondriale,[53] alors que les lésions de type IV sont associées à une mort profonde non apoptotique des oligodendrocytes dans la substance blanche périplaque.

Barnett and Prineas[54] ont analysé les lésions des patients directement après le début d'une rechute, au cours de laquelle la formation de plaque active était en cours. Leurs résultats suggèrent que l'apoptose des oligodendrocytes et l'activation gliale se produisent au cours de la formation précoce de la plaque active en l'absence de lymphocytes inflammatoires ou de phagocytes de myéline. Ils ont proposé que la vulnérabilité des oligodendrocytes, décrite dans le schéma de type III de Lucchinetti, est présente dans les premiers stades de toute formation de plaque et est le déclencheur de la nécrose post-apoptotique ultérieure qui initie la phagocytose de la myéline par les macrophages à des stades ultérieurs. Les analyses in vitro de ce processus ont impliqué des cascades du complément, des facteurs de nécrose tumorale ou des seconds messagers gazeux.[55] Bien que l'identification des plaques et le suivi de leur progression aient une valeur clinique importante, il n'y a qu'une faible corrélation entre la charge des lésions démyélinisantes telle que déterminée par l'IRM conventionnelle et l'incapacité clinique des patients atteints de SEP (voir ci-dessus).

Changements fonctionnels

Les mécanismes d'altération fonctionnelle lors de la démyélinisation incluent souvent la perturbation des ions transmembranaires Na+, K+ et Ca2+, la dispersion de leurs canaux ioniques correspondants, une diminution de l'efficacité de la conduction AP et une crise métabolique qui en résulte (Figure 3). La démyélinisation peut facilement expliquer l'échec de la conduction dans l'axone affecté. Si la conduction n'échoue pas complètement, la vitesse de conduction peut néanmoins être ralentie et un ralentissement différentiel entre différents axones peut entraîner des retards de conduction variables qui entraînent des pointes désynchronisées.

La démyélinisation permet également aux axones dénudés de devenir étroitement apposés, ouvrant ainsi la voie aux interactions éphaptiques et à la diaphonie.[10] La réflexion peut également se produire en raison d'une inadéquation d'impédance entre les longueurs d'axone myélinisées et non myélinisées. D'autre part, l'hyperexcitabilité ne peut pas être directement attribuée à la démyélinisation ; au lieu de cela, des modifications secondaires de l'excitabilité intrinsèque doivent être invoquées pour expliquer des phénomènes tels que la génération de pics ectopiques et la post-décharge (AD). Les altérations de l'excitabilité représentent probablement des changements compensatoires visant à restaurer la fonction suite à la perturbation causée directement par la démyélinisation, conformément à un processus appelé plasticité homéostatique,[56] mais cette compensation peut évidemment être inadaptée. Chacun des résultats susmentionnés, qui ne sont pas mutuellement exclusifs, contribue à produire différents symptômes observés dans les maladies démyélinisantes.

Les symptômes paroxystiques caractérisés par l'apparition soudaine ou l'intensification de symptômes tels que des spasmes ou des douleurs lancinantes résultent probablement de la MA ou de pointes inappropriées de type éclatement. De tels modèles de pointe suggèrent des interactions hautement non linéaires entre le courant ionique contributeurs[57][58] et pourrait, en théorie du moins, impliquer des interactions entre différentes régions du neurone.[59] Contrairement aux formes plus génériques d'hyperexcitabilité (par exemple, augmentation de la cadence de déclenchement ou réduction du seuil), ces schémas spécifiques sont limités en termes de mécanismes précis par lesquels ils pourraient survenir. Par conséquent, l'identification des changements de canaux ioniques sous-jacents à ces formes spécifiques d'hyperexcitabilité peut aider à limiter la recherche de changements de canaux ioniques responsables de formes d'hyperexcitabilité associées, mais moins distinctives.

La perturbation de l'équilibre énergétique dans un neurone pourrait également avoir un impact profond sur le bien-être des neurones (Figure 3). En effet, des modifications compensatoires peuvent parvenir à restaurer certaines fonctions mais, sans renverser le problème primaire, d'autres problèmes peuvent survenir. Par exemple, même si le blocage de la conduction est empêché par une modification compensatoire appropriée de l'excitabilité (c'est-à-dire une modification qui n'entraîne pas d'hyperexcitabilité), le système peut être moins efficace sur le plan énergétique. La perte des économies d'énergie offertes par la conduction saltatoire induit une production d'énergie mitochondriale compensatoire qui peut entraîner des dommages oxydatifs et une neurodégénérescence.[53][60][61]

Garder une trace de cette longue liste de changements neurobiologiques, comprendre les interrelations entre ces changements et finalement lier ces changements aux manifestations cliniques et appliquer un traitement efficace n'est pas une tâche facile. À cette fin, la modélisation informatique est un outil inestimable. Les simulations ne servent pas seulement à organiser les informations déjà connues, elles identifient également des lacunes cruciales dans les connaissances. L'utilisation judicieuse de la modélisation informatique peut donc permettre une compréhension plus complète et faciliter l'application plus efficace de cette compréhension, comme indiqué ci-dessous.

Modélisation informatique

Surtout lorsqu'elle est associée à des expériences traditionnelles, la modélisation informatique est indispensable pour donner un sens aux données incohérentes et aux mécanismes complexes. Ces avantages sont illustrés par l'application de simulations dans d'autres domaines, tels que l'épilepsie.[62] Ici, nous passons en revue une partie de l'histoire de la modélisation informatique des axones, des conductances ioniques, de la physiologie de la myéline et de la démyélinisation, du système immunitaire, des mitochondries et d'autres facteurs biologiques essentiels à la compréhension des maladies démyélinisantes. Notre examen n'est pas exhaustif mais fournira une large introduction aux efforts passés, présents et futurs dans ce domaine.

Modélisation des axones

La modélisation informatique des axones a évolué sur le plan taxonomique, du calmar aux tissus de mammifères avec une augmentation correspondante de la sophistication. Le modèle de Hodgkin et Huxley (HH), qui a fourni la première explication approfondie de la génération d'AP, a été dérivé d'expériences sur des axones géants non myélinisés de calmar,[63][64]mais ce premier modèle s'est avéré être un outil inestimable à partir duquel des modèles ultérieurs plus sophistiqués d'axones myélinisés ont évolué.

L'hétérogénéité spatiale et biophysique conférée par l'ajout de myéline, et la formation conséquente de nœuds et de régions internodales, représente une augmentation significative de la complexité des axones. Le premier modèle informatique d'un axone myélinisé était un modèle unidimensionnel qui effondrait la gaine de myéline dans l'axolemme passif sous-jacent, utilisait une taille de pas spatial uniforme pour former l'approximation discrète utilisée dans la solution numérique et employait une caractérisation HH de la membrane nodale.[65] Goldman & Albus[66] modifié ce modèle pour inclure une description de la membrane nodale dérivée de données expérimentales sur les fibres nerveuses myélinisées de Xenopus laevis telles que déterminées par Frankenhaeuser & Huxley.[67] Des études ultérieures ont utilisé la même forme de base pour le modèle avec quelques variations pour la représentation de l'axolemme.[15][68][69][70][71][72][73][74][75][76]Le modèle à câble unique, décrivant l'axone et toutes ses propriétés de conductance et de capacité dans une équation de câble, a dominé le domaine jusqu'à nos jours malgré l'introduction de modèles à double câble par Blight.[77] Dans les modèles à double câble, l'axolemme internodal et la gaine de myéline sont représentés indépendamment. Le modèle à double câble a été élargi par Halter et Clark[78]explorer les effets de la géométrie complexe des oligodendrocytes du SNC (ou cellules de Schwann dans le cas du SNP).

Les modèles plus récents ont également amélioré les simplifications précédentes, y compris la complexité anatomique du nœud de Ranvier, la distribution des canaux ioniques dans l'axone sous la gaine de myéline, les différentes propriétés électriques de la gaine de myéline et de l'axolemme, et l'accommodation d'un éventuel flux de courant dans l'espace périaxonal.[78][79][80][81][82] Les représentations anatomiques de la zone paranodale ont permis une évaluation plus détaillée des effets des lésions cérébrales traumatiques (TCC) sur les axones myélinisés.[83] L'un des modèles les plus sophistiqués sur le plan anatomique comprend la représentation de la structure complexe de la gaine aqueuse des lamelles de myéline sous la forme d'une série de lamelles parallèles interconnectées dans un modèle de nerfs moteurs..[30][80]

Des modèles plus récents ont également pris en compte la distribution non uniforme des canaux ioniques dans l'axone [19, 84, 85, 86, 87, 88, 89, 90].[19][84][85][86][87][88][89][90] Au-delà des canaux ioniques, les pompes dépendantes de l'énergie et d'autres mécanismes de transport d'ions fournissent des cibles thérapeutiques importantes pour un certain nombre de troubles neurologiques.[91][92][93] À cet égard, la régulation des gradients ioniques transmembranaires coûte beaucoup d'énergie et devient elle-même une considération importante (voir ci-dessous).[94] Cela est d'autant plus vrai que le petit volume d'axones les rend sujets à des changements de concentration d'ions qui peuvent avoir un impact considérable sur les forces motrices et peuvent devenir problématiques dans les modèles qui supposent des concentrations intracellulaires et extracellulaires constantes. Mais des modèles récents ont également traité de tels problèmes (voir ci-dessous).

Tous les modèles susmentionnés se concentrent sur la simulation du changement du potentiel de membrane axonale, mais on n'a pas nécessairement accès expérimental à cette variable, ce qui complique bien sûr les efforts pour comparer les données de simulation et expérimentales. En effet, puisque les enregistrements extracellulaires sont la principale source de données électrophysiologiques de sujets humains, la description mathématique du potentiel de champ extracellulaire est d'un grand intérêt clinique. Des évaluations mathématiques basées sur les équations de Laplace et les transformées de Fourier sont utilisées pour calculer ces potentiels (parfois appelée modélisation ligne-source, par exemple,.[82][95]

Modeling Specific Mechanisms

Beyond modeling normal axonal function, models can be used to explore particular mechanisms of axonal dysfunction especially when combined with experimental results that might better pinpoint mechanisms.[96] For example, Barrett and Barrett[97] showed that the depolarizing afterpotential (DAP) is sensitive to changes in conductance densities and capacitative changes that might occur during demyelination. A model by Blight was designed for simulation of his experimental recording conditions[77][98] and represents a single internode with multiple discrete segments and adjacent nodes and internodes in single lumped-parameter segments. This model included K+ channels in the axolemma of the single multi-segmented internode and treats the remainder as purely passive.

Building on this work, with careful attention to anatomical and electrophysiological details, McIntyre et al.[81] addressed the role of the DAP and afterhyperpolarization (AHP) in the recovery cycle—the distinct pattern of threshold fluctuation following a single action potential exhibited by human nerves. The simulations suggested distinct roles for active and passive Na+ and K+ channels in both afterpotentials and proposed that differences in the AP shape, strength-duration relationship, and the recovery cycle of motor and sensory nerve fibers can be attributed to kinetic differences in nodal Na+ conductances. Richardson et al.[99] also found that alteration to the standard “perfect insulator” model is necessary to reproduce DAPs during high-frequency stimulation.

The temperature sensitivity of demyelination effects has also been investigated computationally. Zlochiver[100] modeled persistent resonant reflection across a single focal demyelination plaque and found that this effect was sensitive to temperature and axon diameter. All of these examples demonstrated the power of simulations to examine specific mechanisms to explain observed phenomena from the clinic and offer guidance for future research.

As mentioned above, distinct changes in axon function are likely to manifest certain gain- or loss-of-function symptoms. If one could reproduce those changes in a computational model, the necessary parameter changes needed to convert the model between normal and abnormal operation could be used to predict the underlying pathology. Ideally this can lead to specific experiments in which the suspect ion channel, for example, is directly manipulated to see if its acute alteration is sufficient to reproduce or reverse certain pathological changes. Recent studies from the Prescott lab illustrate this process.[101][102] This success of these studies depended on advanced techniques including the dynamic clamp technique, used to switch between normal and abnormal spiking patterns and optogenetic tools. The next step is to link changes in axon function with disease symptoms (or their behavioural correlates in animal models).

In auditory nerve experiments, Tagoe and colleagues[103] demonstrated that hearing loss related to morphological changes at paranodes and juxtaparanodes, including the elongation of the auditory nerve around nodes of Ranvier, can result from exposure to lound noise, Extending this work, Hamann and collegues built a computational model to examine possible mechanisms. Their model suggested that it is more likely that a decrease in the density of Na-channels, rather than a redistribution of Na or K channels in general, is responsible for the conduction inhibition associated with acoustic over-exposure.[104] This experiment-model tandem demonstrates the revelatory potential of pairing computational models with laboratory experiments.

With a myelinated axon multi-layered model Stephanova and colleagues have had on-going success identifying likely anatomical and physiological deficiencies underlying various symptoms and conditions related to demyelination by making comparisons to the threshold tracking measurements from patients including latencies, refractoriness (the increase in threshold current during the relative refractory period), refractory period, supernormality, and threshold electrotonus values including stimulus-response measures such as current-threshold relationships.[21] For example, they found that mild internodal systematic demyelination (ISD) is a specific indicator for CMT1A. Mild paranodal systematic demyelination (PSD) and paranodal systematic demyelination (PISD) are specific indicators for CIPD and its subtypes. Severe focal demyelinations, internodal and paranodal, paranodal-internodal (IFD and PFD, PIFD) are specific indicators for acquired demyelinating neuropathies such as GBS and MMN [18] (see Figure 1).

Mild systematic and severe focal demyelination correspond to hereditary (CMT1A) and acquired (CIDP, GBS and MMN) neuropathies (Table 1). It was also found that 70% systematic demyelination is insufficient to cause symptoms and 96% is required for conduction block at a single node [18]. Thus, there is a large safety factor for focal demyelination. With their temperature-dependent version of the model of the myelinated human motor nerve fiber, Stephanova and Daskalova[105] showed that the electrotonic potentials in patients with CIDP are in high risk for blocking during hypo- and even mild hyperthermia and suggest mechanisms involving increased magnitude of polarizing nodal and depolarizing internodal electrotonic potentials, inward rectifier K+ and leak K+ currents increase with temperature, and the accommodation to long-lasting hyperpolarization is greater than to depolarization.

Table 1

Correspondence between types of demyelination and diseases according to Stephanova and Dimitrov.[18]

Type of Demyelination Corresponding Disease (PNS)
Internodal systematic demyelination (ISD) Charcot-Marie-Tooth Disease Type 1A (CMT1A)
Paranodal systematic demyelination (PSD) Chronic inflammatory demyelinating polyneuropathy (CIDP)
Paranodal + internodal demyelination (PISD) Chronic inflammatory demyelinating polyneuropathy (CIPD) subtypes
Internodal focal demyelination (IFD) Guillain-Barré (GBS)
Paranodal focal demyelination (PFD) Multifocal Motor Neuropathy (MMN)
Paranodal + focal demyelination (PIFD) Multifocal Motor Neuropathy (MMN)

Simple Models and Nonlinear Dynamical Analysis

Given the temporal dissociation between the manifestation of symptoms and the rates of demyelination and remyelination, homeostatic processes undoubtedly occur within axons, which include the redistribution of ion channels in demyelinated plaques.[106][107] But given the diversity of ion channels expressed by different axons and only patchy knowledge of how expression levels change, building detailed models to investigate those homeostatic processes is problematic. Especially under those conditions, highly simplified models can help identify fundamental principles, as exemplified by joint use of modified HH and Morris-Lecar models [57,58]. The results of those studies suggested a simple explanation for the breadth of symptoms encountered during demyelination by revealing that the ratio of Na+ to leak K+ conductance, g(Na)/g(L), acted as a four-way switch controlling excitability patterns that included failure of AP propagation, normal AP propagation, AD, and spontaneous spiking.

Further studies with this model suggested the potential for competition or cooperation between different regions of the same neuron.[59] Cooperativity between remote sites of ectopic spiking allows AD to be initiated and maintained at different locations within a single axon, thus providing a compelling explanation for the temporal and spatial discontinuities of pain and other symptoms presented by MS patients. Remarkably, in a recent study of demyelinated axons in a cuprizone mouse model, experimental evidence was seen for a redistribution of ion channels from the node of Ranvier, enhanced ectopic excitability along with antidromically propagated APs from the demyelinated plaque, as well as a compensatory shift in the excitability of membranes proximal to the soma.[108] All of these observations concur or are consistent with the computational model predictions of Coggan and colleagues and imply the success of the computational approach to guiding laboratory studies.

Furthermore, these simplified models enabled application of mathematical tools to examine the nonlinear mechanisms by which AD is initiated and terminated.[57][58][59] Bifurcation analysis revealed the underlying bistability of axon excitability under pathological conditions, as well as the factors controlling the transition from one attractor state to another. AD, for example, requires a slow inward current that allows for two stable attractor states, one corresponding to quiescence and the other to repetitive spiking (a limit cycle). Termination of AD was explained by the attractor associated with repetitive spiking being destroyed. This occurred when ultra-slow negative feedback in the form of intracellular Na+ accumulation caused the destruction of the limit-cycle attractor state [58]. Other studies using bifurcation analysis suggest that ion concentration changes can introduce slow dynamics that may be important for understanding pathological outcomes [94,109].[94][109]

Modeling at Small Scales

Studies mentioned above highlight the importance of ion concentration changes but each of them only considered those changes at a relatively course scale. By comparison, the study by Lorpreore et al.[110] tackled the daunting problem of modeling three-dimensional electro-diffusion of ion fluxes in micro and nano-domains surrounding ion channels at the node of Ranvier. In this unique model, the fluxes of ions are calculated by Poisson-Nernst-Planck equations with finite volume techniques. The fluxes and electric potentials were evaluated within voxels formed by a Delaunay-Voronoi mesh of the axon interior and exterior close to the membrane. Importantly, the algorithm was validated and results agreed with cable model predictions. Divergence from cable model predictions at smaller cluster sizes revealed the importance of each channel’s own electric field.

The above example highlights the point that models can simulate more than ion channels and membrane potential. Indeed, models can and must dig deeper into biophysical mechanisms like electro-diffusion and into signaling pathways that ultimately serve to regulate ion channel function and expression. A promising method called Biochemical Systems Theory (BST) may be useful in the future for pre-screening the effects of drugs at the systemic level. Broome and Coleman[111] demonstrated the power of this technique by modeling several biochemical pathways in neurons associated with cell death during MS including reactive oxygen and nitrogen species formation, Ca2+ dynamics, death complex formation, apoptotic factor release, and inflammatory responses together with three different states: normal, MS disease and treatment. At the atomic-level, a computational model of myelin basic protein (MBP) structure was carried-out because post-translational modifications of MBP may contribute to demyelination in MS.[112] It is important to understand its 3D structure to predict interaction sites with other molecules but a crystal structure for this protein might never be measured directly. This type of modeling may, therefore, represent an effective way to predict the structure by combining knowledge of amino acid sequence with information from similar proteins. The challenge for and the true power of modeling lies in connecting mechanisms that operate at vastly different scales, from molecular structure to the nervous system as a whole, and beyond, to address how the nervous system interacts with the immune system.

Models of Immune Factors. While there are numerous computational models of the immune system,[113] those related to MS typically model genetic interaction networks, either represented as sets of ordinary differential equations (ODEs) or Boolean networks. One systems biology model of a possible cellular mechanism of RRMS found breakdown in homeostasis of effector (Teff) and regulatory T (Treg) cells.[114][115] By changing parameters in the Teff-Treg feedback loop, under continual stochastic external stimulus from antigens, the model reproduced spontaneous and apparently stochastic immune relapses. The irreversible damage from each episode accumulates over time. Novel predictions include the suggestion that the timing of Treg immunotherapy in the immune response cycle is critical in determining whether intervention is beneficial or deleterious.

Models of Mitochondrial Dysfunction. As mentioned above, myelin enables more energy efficient AP conduction along the axon. The increased energy demands placed on the demyelinated axon represents yet another challenge to the afflicted neuron. Beyond the loss of saltatory conduction, there is mounting evidence of a critical role for astrocytes and oligodendrocytes in supplying energy to neurons and this process has also been the subject of computational modeling.[116]

There are many ways mitochondrial function can go awry and the compensatory pathways are equally complicated.[53][60][61] For example, mitochondrial dysfunction can be rooted in perturbed Ca2+ signaling within mitochondria, disrupted proton gradients or electron chain, reduction-oxidation imbalance as well as the consequences of reduced ATP availability, locally and globally. Multi-scale models of heart, for example, have been used to link altered mitochrondrial Ca2+ signaling to arrhythmia [60]. Using mitochondrial network modeling, this study demonstrated how even slightly too much reactive oxygen species can trigger a cell-wide collapse of mitochondrial membrane potential. This is an excellent example of how a computational model can link processes occurring at different levels, and it is precisely these linkages that must be established in the field of demyelination diseases.

Missing Links and the Need for Integration

Within the field of demyelinating diseases, modeling efforts have traditionally focused on axon models aimed at explaining various aspects of excitability. But as outlined above, those models have undergone tremendous evolution in complexity. In the process, models at different biological scales have begun to coalesce. For instance, models have now begun to address the regulation of ion concentrations and the consequences thereof for slow excitability changes, energy consumption, and toxicity. A computational approach will be necessary for integrating parallel and multifactorial etiologies associated with cognitive decline such as immune system signaling, energy metabolism, grey and white matter interactions, and genetic networks [117].[117] These continued efforts are starting to uncover the vast and interconnected feedback loops that operate across a broad range of spatial and temporal scales. That said, such efforts are still in their infancy and wide gaps remain in the modeling of demyelinating diseases. It is easier to describe what has been modeled than what has not. A truly integrated model involving multiple cell types that addresses all the hypothesized etiological factors remains unrealized. Among the unexplored or under-explored but potentially useful targets for modeling are grey matter pathology, myelin sheath aqueous layers, energy metabolism, and perhaps most importantly, multi-scale or integrated modeling. One should recognize that the necessary tools exist in other fields of study and can, therefore, be readily applied to the study of demyelination diseases.

Conclusions

The normal physiological function of the CNS or PNS relies on a highly regulated interplay of neurons, glia, vasculature and immune cells. This process encompasses and integrates numerous cellular and signaling components that produce a dynamical, computational whole. When any part goes awry, the entire system is forced to compensate. Even when compensation manages to rescue the most obvious consequences of demyelination, certain processes may not return to a completely normal state, which can lead to problems on longer time scales. The resulting symptoms are a confusing mixture of direct and compensatory changes that continuously evolve. The overall complexity has proven to be intractable to efficient experimental dissection. The application of computational modeling techniques represents an invaluable approach to help break the impasse and engender a new era of understanding and discovery.

Acknowledgments

Support provided by the Canadian Institutes of Health Research New Investigator Award and the Ontario Early Researcher Award (SAP). We thank Heiki Blum for assistance with figure preparation.

Author Contributions

All authors contributed to the writing of this manuscript. Figures were provided by Sven G. Meuth.

Conflicts of Interest

The authors declare no conflict of interest.

Article information

Int J Mol Sci. 2015 Sep; 16(9): 21215–21236. Published online 2015 Sep 7. doi: 10.3390/ijms160921215 PMCID: PMC4613250 PMID: 26370960 Jay S. Coggan,1,* Stefan Bittner,2 Klaus M. Stiefel,1 Sven G. Meuth,2 and Steven A. Prescott3,4 Christoph Kleinschnitz, Academic Editor 1NeuroLinx Research Institute, La Jolla, CA 92039, USA; E-Mail: gro.xniloruen@sualk 2Department of Neurology, Institute of Physiology, Universitätsklinikum Münster, 48149 Münster, Germany; E-Mails: moc.kooltuo@renttib-nafets (S.B.); ed.retsneumku@htuem.nevs (S.G.M.) 3Neurosciences and Mental Health, the Hospital for Sick Children, Toronto, ON M5G 1X8, Canada; E-Mail: ac.sdikkcis@ttocserp.evets 4Department of Physiology and the Institute of Biomaterials and Biomedical Engineering, University of Toronto, Toronto, ON M5G 1X8, Canada

  • Author to whom correspondence should be addressed; E-Mail: gro.xniloruen@yaj; Tel.: +1-858-243-6720.

Received 2015 May 26; Accepted 2015 Aug 25. Copyright © 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/). Articles from International Journal of Molecular Sciences are provided here courtesy of Multidisciplinary Digital Publishing Institute (MDPI)

Bibliography

  1. ↑ Virchow R. Uber das ausgebreitete Vorkommen einer dem Nervenmark analogen Substanz in den tierischen Geweben. Virchows Arch. Pathol. Anat. 1854;6:562–572. doi: 10.1007/BF02116709. [CrossRef] [Google Scholar]
  2. ↑ Stiefel K.M., Torben-Nielsen B., Coggan J.S. Proposed evolutionary changes in the role of myelin. Front. Neurosci. 2013;8 doi: 10.3389/fnins.2013.00202.[PMC free article] [PubMed] [CrossRef] [Google Scholar]
  3. ↑ Bullock T.H., Moore J.K., Fields R.D. Evolution of myelin sheaths: Both lamprey and hagfish lack myelin. Neurosci. Lett. 1984;48:145–148. doi: 10.1016/0304-3940(84)90010-7. [PubMed] [CrossRef] [Google Scholar]
  4. ↑ Davis A.D., Weatherby T.M., Hartline D.K., Lenz P.H. Myelin-like sheaths in copepod axons. Nature. 1999;398:571–571. doi: 10.1038/19212. [PubMed] [CrossRef] [Google Scholar]
  5. ↑ Hartline D.K., Colman D.R. Rapid conduction and the evolution of giant axons and myelinated fibers. Curr. Biol. 2007;17:R29–R35. doi: 10.1016/j.cub.2006.11.042. [PubMed] [CrossRef] [Google Scholar]
  6. ↑ Arancibia-Carcamo I.L., Attwell D. The node of ranvier in CNS pathology. Acta Neuropathol. 2014;128:161–175. doi: 10.1007/s00401-014-1305-z.[PMC free article] [PubMed] [CrossRef] [Google Scholar]
  7. ↑ Faisal A.A., White J.A., Laughlin S.B. Ion-channel noise places limits on the miniaturization of the brain’s wiring. Curr. Biol. 2005;15:1143–1149. doi: 10.1016/j.cub.2005.05.056. [PubMed] [CrossRef] [Google Scholar]
  8. ↑ Babbs C.F., Riyi S. Subtle paranodal injury slows impulse conduction in a mathematical model of myelinated axons. PLoS ONE. 2013;8:e67767. doi: 10.1371/journal.pone.0067767. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
  9. ↑ 9.0 9.1 9.2 Trapp B.D., Nave K.A. Multiple sclerosis: An immune or neurodegenerative disorder? Annu. Rev. Neurosci. 2008;31:247–69. doi: 10.1146/annurev.neuro.30.051606.094313. [PubMed] [CrossRef] [Google Scholar]
  10. ↑ 10.0 10.1 10.2 10.3 Compston A., Coles A. Multiple sclerosis. Lancet. 2008;372:1502–1517. doi: 10.1016/S0140-6736(08)61620-7. [PubMed] [CrossRef] [Google Scholar]
  11. ↑ Ostermann P.O., Westerberg C.E. Paroxysmal attacks in multiple sclerosis. Brain. 1975;98:189–202. doi: 10.1093/brain/98.2.189. [PubMed] [CrossRef] [Google Scholar]
  12. ↑ Twomey J.A., Espir M.L. Paroxysmal symptoms as the first manifestations of multiple sclerosis. J. Neurol. Neurosurg. Psychiatry. 1980;43:296–304. doi: 10.1136/jnnp.43.4.296. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
  13. ↑ Seewann A., Vrenken H., van der Valk P., Blezer E.L., Knol D.L., Castelijns J.A., Polman C.H., Pouwels P.J., Barkhof F., Geurts J.J. Diffusely abnormal white matter in chronic multiple sclerosis: Imaging and histopathologic analysis. Arch. Neurol. 2009;66:601–609. doi: 10.1001/archneurol.2009.57. [PubMed] [CrossRef] [Google Scholar]
  14. ↑ Ceccarelli A., Bakshi R., Neema M. MRI in multiple sclerosis: A review of the current literature. Curr. Opin. Neurol. 2012;25:402–409. doi: 10.1097/WCO.0b013e328354f63f. [PubMed] [CrossRef] [Google Scholar]
  15. ↑ 15.0 15.1 Moore J.W., Joyner R.W., Brill M.H., Waxman S.D., Najar-Joa M. Simulations of conduction in uniform myelinated fibers. Relative sensitivity to changes in nodal and internodal parameters. Biophys. J. 1978;21:147–160. doi: 10.1016/S0006-3495(78)85515-5. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
  16. ↑ Waxman S.G., Kocsis J.D., Stys P.K.  The Axon: Structure, Function and Pathophysiology. Oxford University Press; New York, NY, USA: 1995. [Google Scholar]
  17. ↑ Polman C.H., Reingold S.C., Banwell B., Clanet M., Cohen J.A., Filippi M., Fujihara K., Havrdova E., Hutchinson M., Kappos L., et al. Diagnostic criteria for multiple sclerosis: 2010 revisions to the McDonald criteria. Ann. Neurol. 2011;69:292–302. doi: 10.1002/ana.22366. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
  18. ↑ 18.0 18.1 Stephanova D.I., Dimitrov B.  Computational Neuroscience: Simulated Demyelinating Neuropathies and Neuronopathies. CRC Press; Boca Raton, FL, USA: 2013.  [Google Scholar]
  19. ↑ 19.0 19.1 Bostock H., Baker M., Reid G. Changes in excitability of human motor axons underlying post-ischaemic fasciculations: Evidence for two stable states. J. Physiol. 1991;441:537–557. doi: 10.1113/jphysiol.1991.sp018766.[PMC free article] [PubMed] [CrossRef] [Google Scholar]
  20. ↑ Mogyoros I., Kiernan M.C., Burke D., Bostock H. Strength-duration properties of sensory and motor axons in amyotrophic lateral sclerosis. Brain. 1998;121:851–859. doi: 10.1093/brain/121.5.851. [PubMed] [CrossRef] [Google Scholar]
  21. ↑ 21.0 21.1 Kiernan M.C., Burke D., Andersen K.V., Bostock H. Multiple measures of axonal excitability: A new approach in clinical testing. Muscle Nerve. 2000;23:399–409. doi: 10.1002/(SICI)1097-4598(200003)23:3<399::AID-MUS12>3.0.CO;2-G. [PubMed] [CrossRef] [Google Scholar]
  22. ↑ Cappelen-Smith C., Kuwabara S., Lin C.S., Mogyoros I., Burke D. Membrane properties in chronic inflammatory demyelinating polyneuropathy. Brain. 2001;124:2439–2447. doi: 10.1093/brain/124.12.2439. [PubMed] [CrossRef] [Google Scholar]
  23. ↑ Kuwabara S., Ogawara K., Sung J.Y., Mori M., Kanai K., Hattori T., Yuki N., MLin C.S., Burke D., Bostock H. Differences in membrane properties of axonal and demyelinating Guillain-Barré syndromes. Ann. Neurol. 2002;52:180–187. doi: 10.1002/ana.10275. [PubMed] [CrossRef] [Google Scholar]
  24. ↑ Nodera H., Bostock H., Kuwabara S., Sakamoto T., Asanuma K., Jia-Ying S., Ogawara K., Hattori N., Hirayama M., Sobue G., et al. Nerve excitability properties in Charcot-Marie-Tooth disease type 1A. Brain. 2004;127:203–211. doi: 10.1093/brain/awh020. [PubMed] [CrossRef] [Google Scholar]
  25. ↑ Sung M.H., Simon R. In silico simulation of inhibitor drug effects on nuclear factor-κB pathway dynamics. Mol. Pharmacol. 2004;66:70–75. doi: 10.1124/mol.66.1.70. [PubMed] [CrossRef] [Google Scholar]
  26. ↑ Stephanova D.I., Daskalova M. Differences in potentials and excitability properties in simulated cases of demyelinating neuropathies. Part III. Paranodal internodal demyelination. Clin. Neurophysiol. 2005;116:2334–2341. doi: 10.1016/j.clinph.2005.07.013. [PubMed] [CrossRef] [Google Scholar]
  27. ↑ Stephanova D.I., Daskalova M.S. Differences between the channels, currents and mechanisms of conduction slowing/block and accommodative processes in simulated cases of focal demyelinating neuropathies. Eur. Biophys. J. 2008;37:829–842. doi: 10.1007/s00249-008-0284-1. [PubMed] [CrossRef] [Google Scholar]
  28. ↑ Stephanova D.I., Alexandrov A.S. Simulating mild systematic and focal demyelinating neuropathies: Membrane property abnormalities. J. Integr. Neurosci. 2006;5:595–623. doi: 10.1142/S0219635206001331. [PubMed] [CrossRef] [Google Scholar]
  29. ↑ Stephanova D.I., Daskalova M., Alexandrov A.S. Channels, currents and mechanisms of accommodative processes in simulated cases of systematic demyelinating neuropathies. Brain Res. 2007;1171:138–151. doi: 10.1016/j.brainres.2007.07.029. [PubMed] [CrossRef] [Google Scholar]
  30. ↑ 30.0 30.1 Stephanova D.I., Krustev S.M., Negrev N., Daskalova M. The myelin sheath aqueous layers improve the membrane properties of simulated chronic demyelinating neuropathies. J. Integr. Neurosci. 2011;10:105–120. doi: 10.1142/S0219635211002646. [PubMed] [CrossRef] [Google Scholar]
  31. ↑ Stephanova D.I., Alexandrov A.S., Kossev A., Christova L. Simulating focal demyelinating neuropathies: Membrane property abnormalities. Biol. Cybern. 2007;96:195–208. doi: 10.1007/s00422-006-0113-5. [PubMed] [CrossRef] [Google Scholar]
  32. ↑ Bø L., Geurts J.J., Mörk S.J., van der Valk P. Grey matter pathology in multiple sclerosis. Acta Neurol. Scand. Suppl. 2006;183:48–50. doi: 10.1111/j.1600-0404.2006.00615.x. [PubMed] [CrossRef] [Google Scholar]
  33. ↑ Geurts J.J., Barkhof F. Grey matter pathology in multiple sclerosis. Lancet Neurol. 2008;7:841–851. doi: 10.1016/S1474-4422(08)70191-1. [PubMed] [CrossRef] [Google Scholar]
  34. ↑ Zivadinov R., Pirko I. Advances in understanding gray matter pathology in multiple sclerosis: Are we ready to redefine disease pathogenesis? BMC Neurol. 2012;12 doi: 10.1186/1471-2377-12-9. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
  35. ↑ Popescu B.F., Lucchinetti C.F. Pathology of demyelinating diseases. Annu. Rev. Pathol. 2012;7:185–217. doi: 10.1146/annurev-pathol-011811-132443.[PubMed] [CrossRef] [Google Scholar]
  36. ↑ Kurtzke J.F., Beebe G.W., Nagler B., Nefzger M.D., Auth T.L., Kurland L.T. Studies on the natural history of multiple sclerosis: V. Long-term survival in young men. Arch. Neurol. 1970;22:215–225. doi: 10.1001/archneur.1970.00480210025003. [PubMed] [CrossRef] [Google Scholar]
  37. ↑ Rao S.M., Leo G.J., Bernardin L., Unverzagt F. Cognitive dysfunction in multiple sclerosis. I. Frequency, patterns, and prediction. Neurology. 1991;41:685–691. doi: 10.1212/WNL.41.5.685. [PubMed] [CrossRef] [Google Scholar]
  38. ↑ Meuth S.G., Bittner S., Ulzheimer J.C., Kleinschnitz C., Kieseier B.C., Wiendl H. Therapeutic approaches to multiple sclerosis: An update on failed, interrupted, or inconclusive trials of neuroprotective and alternative treatment strategies. BioDrugs. 2010;24:317–330. doi: 10.2165/11537190-000000000-00000. [PubMed] [CrossRef] [Google Scholar]
  39. ↑ Goldenberg M.M. Multiple sclerosis review. Pharm. Ther. 2012;37:137–139.[PMC free article] [PubMed] [Google Scholar]
  40. ↑ Göbel K., Wedell J.H., Herrmann A.M., Wachsmuth L., Pankratz S., Bittner S., Budde T., Kleinschnitz C., Faber C., Wiendl H., et al. 4-Aminopyridine ameliorates mobility but not disease course in an animal model of multiple sclerosis. Exp. Neurol. 2013;248:62–71. doi: 10.1016/j.expneurol.2013.05.016.[PubMed] [CrossRef] [Google Scholar]
  41. ↑ Krishnan A.V., Kiernan M.C. Sustained-release fampridine and the role of ion channel dysfunction in multiple sclerosis. Mult. Scler. 2013;19:385–391. doi: 10.1177/1352458512463769. [PubMed] [CrossRef] [Google Scholar]
  42. ↑ Bowe C.M., Kocsis J.D., Targ E.F., Waxman S.G. Physiological effects of 4-aminopyridine on demyelinated mammalian motor and sensory fibers. Ann. Neurol. 1987;22:264–268. doi: 10.1002/ana.410220212. [PubMed] [CrossRef] [Google Scholar]
  43. ↑ Sakurai M., Kanazawa I. Positive symptoms in multiple sclerosis: Their treatment with sodium channel blockers, lidocaine and mexiletine. J. Neurol. Sci. 1999;162:162–168. doi: 10.1016/S0022-510X(98)00322-0. [PubMed]
  44. ↑ Mattson M.P., Guthrie P.B., Kater S.B. A role for Na+-dependent Ca2+extrusion in protection against neuronal excitotoxicity. FASEB J. 1989;3:2519–2526. [PubMed] [Google Scholar]
  45. ↑ Moll N.M., Rietsch A.M., Thomas S., Ransohoff A.J., Lee J.C., Fox R., Chang A., Ransohoff R.M., Fisher E. Multiple sclerosis normal-appearing white matter: Pathology-imagig correlations. Ann. Neurol. 2011;70:764–773. doi: 10.1002/ana.22521. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
  46. ↑ 46.0 46.1 Lucchinetti C., Brück W., Parisi J., Scheithauer B., Rodriguez M., Lassmann H. Heterogeneity of multiple sclerosis lesions: Implications for the pathogenesis of demyelination. Ann. Neurol. 2000;47:707–717. doi: 10.1002/1531-8249(200006)47:6<707::AID-ANA3>3.0.CO;2-Q. [PubMed] [CrossRef] [Google Scholar]
  47. ↑ Kassmann C.M., Nave K.A. Oligodendroglial impact on axonal function and survival— A hypothesis. Curr. Opin. Neurol. 2008;21:235–241. doi: 10.1097/WCO.0b013e328300c71f. [PubMed] [CrossRef] [Google Scholar]
  48. ↑ Scolding N., Franklin R. Axon loss in multiple sclerosis. Lancet. 1998;352:340–341. doi: 10.1016/S0140-6736(05)60463-1. [PubMed] [CrossRef] [Google Scholar]
  49. ↑ Mi S., Miller R.H., Lee X., Scott M.L., Shulag-Morskaya S., Shao Z., Chang J., Thill G., Levesque M., Zhang M., et al. LINGO-1 negatively regulates myelination by oligodendrocytes. Nat. Neurosci. 2005;8:745–751. doi: 10.1038/nn1460. [PubMed] [CrossRef] [Google Scholar]
  50. ↑ Bittner S., Ruck T., Schuhmann M.K., Herrmann A.M., Maati H.M., Bobak N., Göbel K., Langhauser F., Stegner D., Ehling P., et al. 2013 Endothelial TWIK-related potassium channel-1 (TREK1) regulates immune-cell trafficking into the CNS. Nat. Med. 2013;19:1161–1165. doi: 10.1038/nm.3303. [PubMed]
  51. ↑ Viglietta V., Baecher-Allan C., Weiner H.L., Hafler D.A. Loss of functional suppression by CD4+CD25+ regulatory T cells in patients with multiple sclerosis. J. Exp. Med. 2004;199:971–999. doi: 10.1084/jem.20031579.[PMC free article] [PubMed] [CrossRef] [Google Scholar]
  52. ↑ Zajicek J.P., Wing M., Scolding N.J., Compston D.A. Interactions between oligodendrocytes and microglia. A major role for complement and tumour necrosis factor in oligodendrocyte adherence and killing. Brain. 1992;115:1611–1631. [PubMed] [Google Scholar]
  53. ↑ 53.0 53.1 53.2 Nikić I., Merkler D., Sorbara C., Brinkoetter M., Kreutzfeldt M., Bareyre F.M., Brück W., Bishop D., Misgeld T., Kerschensteiner M. A reversible form of axon damage in experimental autoimmune encephalomyelitis and multiple sclerosis. Nat. Med. 2011;17:495–499. doi: 10.1038/nm.2324. [PubMed] [CrossRef] [Google Scholar]
  54. ↑ Barnett M.H., Prineas J.W. Relapsing and remitting multiple sclerosis: Pathology of the newly forming lesion. Ann. Neurol. 2004;55:458–468. doi: 10.1002/ana.20016. [PubMed] [CrossRef] [Google Scholar]
  55. ↑ Van der Laan L.J., Ruuls S.R., Weber K.S., Lodder I.J., Döpp E.A., Dijkstra C.D. Macrophage phagocytosis of myelin in vitro determined by flow cytometry: Phagocytosis is mediated by CR3 and induces production of tumor necrosis factor-α and nitric oxide. J. Neuroimmunol. 1996;70:145–152. doi: 10.1016/S0165-5728(96)00110-5. [PubMed] [CrossRef] [Google Scholar]
  56. ↑ Wang G., Thompson S.M. Maladaptive homeostatic plasticity in a rodent model of central pain syndrome: Thalamic hyperexcitability after spinothalamic tract lesions. J. Neurosci. 2008;28:11959–11969. doi: 10.1523/JNEUROSCI.3296-08.2008. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
  57. ↑ 57.0 57.1 Coggan J.S., Prescott S.A., Bartol T.M., Sejnowski T.J. Imbalance of ionic conductances contributes to diverse symptoms of demyelination. Proc. Natl. Acad. Sci. USA. 2010;107:20602–20609. doi: 10.1073/pnas.1013798107.[PMC free article] [PubMed] [CrossRef] [Google Scholar]
  58. ↑ 58.0 58.1 Coggan J.S., Ocker G.K., Sejnowski T.J., Prescott S.A. Explaining pathological changes in axonal excitability through dynamical analysis of conductance-based models. J. Neural Eng. 2011;8 doi: 10.1088/1741-2560/8/6/065002. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
  59. ↑ 59.0 59.1 59.2 Coggan J.S., Prescott S.A., Sejnowski T.J. Cooperativity between remote sites of ectopic spiking allows afterdischarge to be initiated and maintained at different locations. J. Comput. Neurosci. 2015;39:17–28. doi: 10.1007/s10827-015-0562-8. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
  60. ↑ 60.0 60.1 Aon M.A., Cortassa S., Akar F.G., Brown D.A., Zhou L., O’Rourke B. From mitochondrial dynamics to arrhythmias. Int. J. Biochem. Cell Biol. 2009;41:1940–1948. doi: 10.1016/j.biocel.2009.02.016. [PMC free article][PubMed] [CrossRef] [Google Scholar]
  61. ↑ 61.0 61.1 Su K., Bourdette D., Forte M. Mitochondrial dysfunction and neurodegeneration in multiple sclerosis. Front. Physiol. 2013;4doi: 10.3389/fphys.2013.00169. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
  62. ↑ Soltesz I., Staley K.  Computational Neuroscience in Epilepsy. 1st ed. Elsevier; London, UK: 2008.  [Google Scholar]
  63. ↑ Hodgkin A.L., Huxley A.F. The components of membrane conductance in the giant axon of Loligo. J. Physiol. 1952;116:473–496. doi: 10.1113/jphysiol.1952.sp004718. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
  64. ↑ Hodgkin A.L., Huxley A.F. Currents carried by sodium and potassium ions through the membrane of the giant axon of Loligo. J. Physiol. 1952;116:449–472. doi: 10.1113/jphysiol.1952.sp004717. [PMC free article] [PubMed]
  65. ↑ Fitzhugh R. Computation of impulse initiation and saltatory conduction in a myelinated nerve fiber. Biophys. J. 1962;2:11–21. doi: 10.1016/S0006-3495(62)86837-4. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
  66. ↑ Goldman L., Albus J.S. Computation of impulse conduction in myelinated fibers; theoretical basis of the velocity-diameter relation. Biophys. J. 1968;8:596–607. doi: 10.1016/S0006-3495(68)86510-5. [PMC free article][PubMed] [CrossRef] [Google Scholar]
  67. ↑ Frankenhaeuser B., Huxley A.F. The action potential in the myelinated nerve fiber of Xenopus laevis as computed on the basis of voltage clamp data. J. Physiol. 1964;171:302–315. doi: 10.1113/jphysiol.1964.sp007378.[PMC free article] [PubMed] [CrossRef] [Google Scholar]
  68. ↑ Smith R.S., Koles Z.J. Myelinated nerve fibers: Computed effect of myelin thickness on conduction velocity. Am. J. Physiol. 1970;219:1256–1258.[PubMed] [Google Scholar]
  69. ↑ Hutchinson N.A., Koles Z.J., Smith R.S. Conduction velocity in myelinated nerve fibres of Xenopus laevis. J. Physiol. 1970;208:279–289. doi: 10.1113/jphysiol.1970.sp009119. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
  70. ↑ Koles Z.J., Rasminsky M. A computer simulation of conduction in demyelinated nerve fibres. J. Physiol. 1972;227:351–364. doi: 10.1113/jphysiol.1972.sp010036. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
  71. ↑ Hardy W.L. Propagation speed in myelinated nerve. II. Theoretical dependence on external Na and on temperature. Biophys. J. 1973;13:1071–1089. doi: 10.1016/S0006-3495(73)86046-1. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
  72. ↑ Schauf C.L., Davis F.A. Impulse conduction in multiple sclerosis: A theoretical basis for modification by temperature and pharmacological agents. J. Neurol. Neurosurg. Psychiatry. 1974;37:152–161. doi: 10.1136/jnnp.37.2.152.[PMC free article] [PubMed] [CrossRef] [Google Scholar]
  73. ↑ Brill M.H., Waxman S.G., Moore J.W., Joyner R.W. Conduction velocity and spike configuration in myelinated fibres: Computed dependence on internode distance. J. Neurol. Neurosurg. Psychiatry. 1977;40:769–774. doi: 10.1136/jnnp.40.8.769. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
  74. ↑ Waxman S.G., Brill M.H. Conduction through demyelinated plaques in multiple sclerosis: Computer simulations of facilitation by short internodes. J. Neurol. Neurosurg. Psychiatry. 1978;41:408–416. doi: 10.1136/jnnp.41.5.408.[PMC free article] [PubMed] [CrossRef] [Google Scholar]
  75. ↑ Wood S.L., Waxman S.G., Kocsis J.D. Conduction of trans of impulses in uniform myelinated fibers: Computed dependence on stimulus frequency. Neuroscience. 1982;7:423–430. doi: 10.1016/0306-4522(82)90276-7. [PubMed] [CrossRef] [Google Scholar]
  76. ↑ Goldfinger M.D. Computation of high safety factor impulse propagation at axonal branch points. Neuroreport. 2000;11:449–456. doi: 10.1097/00001756-200002280-00005. [PubMed] [CrossRef] [Google Scholar]
  77. ↑ 77.0 77.1 Blight A.R. Computer simulation of action potentials and afterpotentials in mammalian myelinated axons: The case for a lower resistance myelin sheath. Neuroscience. 1985;15:13–31. doi: 10.1016/0306-4522(85)90119-8. [PubMed] [CrossRef] [Google Scholar]
  78. ↑ 78.0 78.1 Halter J.A., Clark J.W., Jr. A distributed-parameter model of the myelinated nerve fiber. J. Theor. Biol. 1991;148:345–382. doi: 10.1016/S0022-5193(05)80242-5. [PubMed] [CrossRef] [Google Scholar]
  79. ↑ Schwarz J.R., Eikhof G. Na currents and action potentials in rat myelinated nerve fibres at 20 and 37 °C. Pflugers Arch. 1987;409:569–577. doi: 10.1007/BF00584655. [PubMed] [CrossRef] [Google Scholar]
  80. ↑ 80.0 80.1 Stephanova D.I. Myelin as longitudinal conductor: A multi-layered model of the myelinated human motor nerve fibre. Biol. Cybern. 2001;84:301–308. doi: 10.1007/s004220000213. [PubMed] [CrossRef] [Google Scholar]
  81. ↑ 81.0 81.1 McIntyre C.C., Richardson A.G., Grill W.M. Modeling the excitability of mammalian nerve fibers: Influence of afterpotentials on the recovery cycle. J. Neurophysiol. 2002;87:995–1006. [PubMed] [Google Scholar]
  82. ↑ 82.0 82.1 Einziger P.D., Livshitz L.M., Mizrahi J. Generalized cable equation model for myelinated nerve fiber. IEEE Trans. Biomed. Eng. 2005;52:1632–1642. doi: 10.1109/TBME.2005.856031. [PubMed] [CrossRef] [Google Scholar]
  83. ↑ Volman V., Ng L. Primary paranode demyelination modulates slowly developing axonal depolarization in a model of axonal injury. J. Neural Comput. 2014;37:439–457. [PubMed] [Google Scholar]
  84. ↑ Stephanova D.I., Bostock H. A Distributed-parameter model of the myelinated human motor nerve fibre: Temporal and spatial distributions of action potentials and ionic currents. Biol. Cybern. 1995;73:275–280. doi: 10.1007/BF00201429. [PubMed] [CrossRef] [Google Scholar]
  85. ↑ Chiu S.Y., Ritchie J.M. On the physiological role of internodal potassium channels and the security of conduction in myelinated nerve fibres. Proc. R. Soc. Lond. B Biol. Sci. 1984;220:415–422. doi: 10.1098/rspb.1984.0010.[PubMed] [CrossRef] [Google Scholar]
  86. ↑ Brismar T., Schwarz J.R. Potassium permeability in rat myelinated nerve fibres. Acta Physiol. Scand. 1985;124:141–148. doi: 10.1111/j.1748-1716.1985.tb07645.x. [PubMed] [CrossRef] [Google Scholar]
  87. ↑ Chiu S.Y., Schwarz W. Sodium and potassium currents in acutely demyelinated internodes of rabbit sciatic nerves. J. Physiol. 1987;391:631–649. doi: 10.1113/jphysiol.1987.sp016760. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
  88. ↑ Baker M., Bostock H., Grafe P., Martius P. Function and distribution of three types of rectifying channel in rat spinal root myelinated axons. J. Physiol. 1987;383:45–67. [PMC free article] [PubMed] [Google Scholar
  89. ↑ Röper J., Schwarz J.R. Heterogeneous distribution of fast and slow potassium channels in myelinated rat nerve fibres. J. Physiol. 1989;416:93–110. doi: 10.1113/jphysiol.1989.sp017751. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
  90. ↑ Bittner S., Meuth S.G. Targeting ion channels for the treatment of autoimmune neuroinflammation. Ther. Adv. Neurol. Disord. 2013;6:322–336. doi: 10.1177/1756285613487782. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
  91. ↑ Waxman S.G., Ritchie J.M. Molecular dissection of the myelinated axon. Ann. Neurol. 1993;33:121–136. doi: 10.1002/ana.410330202. [PubMed] [CrossRef] [Google Scholar]
  92. ↑ Bittner S., Budde T., Wiendl H., Meuth S.G. From the background to the spotlight: TASK channels in pathological conditions. Brain Pathol. 2010;20:999–1009. doi: 10.1111/j.1750-3639.2010.00407.x. [PMC free article][PubMed] [CrossRef] [Google Scholar]
  93. ↑ Ehling P., Bittner S., Budde T., Wiendl H., Meuth S.G. Ion channels in autoimmune neurodegeneration. FEBS Lett. 2011;585:3836–3842. doi: 10.1016/j.febslet.2011.03.065. [PubMed] [CrossRef] [Google Scholar]
  94. ↑ 94.0 94.1 Hübel N., Dahlem M.A. Dynamics from seconds to hours in Hodgkin-Huxley model with time-dependent ion concentrations and buffer reservoirs. PLoS Comput. Biol. 2014;10:e1003941. doi: 10.1371/journal.pcbi.1003941.[PMC free article] [PubMed] [CrossRef] [Google Scholar]
  95. ↑ Ganapathy L., Clark J.W. Extracellular currents and potentials of the active myelinated nerve fibre. Biophys. J. 1987;52:749–761. doi: 10.1016/S0006-3495(87)83269-1. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
  96. ↑ Prescott S.A. Pathological changes in peripheral nerve excitability. In: Jaeger D., Jung R., editors. Encyclopedia of Computational Neurosci. 1st ed. Springer-Verlag; New York, NY, USA: 2015.  [Google Scholar]
  97. ↑ Barrett E.F., Barrett J.N. Intracellular recording from vertebrate myelinated axons: Mechanism of the depolarizing afterpotential. J. Physiol. 1982;323:117–144. doi: 10.1113/jphysiol.1982.sp014064. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
  98. ↑ Blight A.R., Someya S. Depolarizing afterpotentials in myelinated axons of mammalian spinal cord. Neuroscience. 1985;15:1–12. doi: 10.1016/0306-4522(85)90118-6. [PubMed] [CrossRef] [Google Scholar]
  99. ↑ Richardson A.G., McIntyre C.C., Grill W.M. Modelling the effects of electric fields on nerve fibres: Influence of the myelin sheath. Med. Biol. Eng. Comput. 2000;38:438–446. doi: 10.1007/BF02345014. [PubMed] [CrossRef] [Google Scholar]
  100. ↑ Zlochiver S. Persistent reflection underlies ectopic activity in multiple sclerosis: A numerical study. Biol. Cybern. 2010;102:181–196. doi: 10.1007/s00422-009-0361-2. [PubMed] [CrossRef] [Google Scholar]
  101. ↑ Ratté S., Zhu Y., Lee K.Y., Prescott S.A. Criticality and degeneracy in injury-induced changes in primary afferent excitability and the implications for neuropathic pain. Elife. 2014;3:e02370. doi: 10.7554/eLife.02370.[PMC free article] [PubMed] [CrossRef] [Google Scholar]
  102. ↑ Zhu Y., Feng B., Schwartz E.S., Gebhart G.F., Prescott S.A. Novel method to assess axonal excitability using channelrhodopsin-based photoactivation. J. Neurophysiol. 2015;113:2242–2249. doi: 10.1152/jn.00982.2014.[PMC free article] [PubMed] [CrossRef] [Google Scholar]
  103. ↑ Tagoe T., Barker M., Jones A., Allcock N., Hamann M. Auditory nerve perinodal dysmyelination in noise-induced hearing loss. J. Neurosci. 2014;12:2684–2688. doi: 10.1523/JNEUROSCI.3977-13.2014.
  104. ↑ Brown A.M., Hamann M. Computational modeling of the effects of auditory nerve dysmyelination. Front. Neuroanat. 2014;8doi: 10.3389/fnana.2014.00073. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
  105. ↑ Stephanova D.I., Daskalova M. Electrotonic potentials in simulated chronic inflammatory demyelinating polyneuropathy at 20 °C–42 °C. J. Integr. Neurosci. 2015;27:1–18. doi: 10.1142/S0219635215500119. [PubMed] [CrossRef] [Google Scholar]
  106. ↑ Rasminsky M. Hyperexcitability of pathologically myelinated axons and positive symptoms in multiple sclerosis. Adv. Neurol. 1981;31:289–297.[PubMed] [Google Scholar]
  107. ↑ Ulrich J., Groebke-Lorenz W. The optic nerve in multiple sclerosis: A morphological study with retrospective clinicopathological correlation. Neuro-Ophthalmology. 1983;3:149–159. doi: 10.3109/01658108309009732.[CrossRef] [Google Scholar]
  108. ↑ Hamada M.S., Kole M.H. Myelin loss and axonal ion channel adaptations associated with gray matter neuronal hyperexcitability. J. Neurosci. 2015;35:7272–7786. [PMC free article] [PubMed] [Google Scholar]
  109. ↑ Yu N., Morris C.E., Joós B., Longtin A. Spontaneous excitation patterns computed for axons with injury-like impairments of sodium channels and Na/K pumps. PLoS Comput. Biol. 2012;8:e1002664. doi: 10.1371/journal.pcbi.1002664. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
  110. ↑ Lopreore C.L., Bartol T.M., Coggan J.S., Keller D.X., Sosinsky G.E., Ellisman M.H., Sejnowski T.J. Computational modeling of three-dimensional electrodiffusion in biological systems: Application to the node of Ranvier. Biophys. J. 2008;95:2624–2635. doi: 10.1529/biophysj.108.132167.
  111. ↑ Broome T.M., Cole.man R.A. A mathematical model of cell death in multiple sclerosis. J. Neurosci. Methods. 2011;201:420–425. doi: 10.1016/j.jneumeth.2011.08.008. [PubMed] [CrossRef] [Google Scholar]
  112. ↑ Ridsdale R.A., Beniac D.R., Tompkins T.A., Moscarello M.A., Harauz G. Three-dimensional structure of myelin basic protein. II. Molecular modeling and considerations of predicted structures in multiple sclerosis. J. Biol. Chem. 1997;272:4269–4275. doi: 10.1074/jbc.272.7.4269. [PubMed] [CrossRef] [Google Scholar]
  113. ↑ Pigozzo A.B., Macedo G.C., Santos R.W., Lobosco M. On the computational modeling of the innate immune system. BMC Bioinform. 2013;14 doi: 10.1186/1471-2105-14-S6-S7. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
  114. ↑ Doerck S., Göbel K., Weise G., Schneider-Hohendorf T., Reinhardt M., Hauff P., Schwab N., Linker R., Mäurer M., Meuth S.G., et al. Temporal pattern of ICAM-I mediated regulatory T cell recruitment to sites of inflammation in adoptive transfer model of multiple sclerosis. PLoS ONE. 2010;5:e15478. doi: 10.1371/journal.pone.0015478. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
  115. ↑ De Mendizábal N.V., Carneiro J., Solé R.V., Goñi J., Bragard J., Martinez-Forero I., Martinez-Pasamar S., Sepulcre J., Torrealdea J., Bagnato F., et al. Modeling the effector-regulatory T cell cross-regulation reveals the intrinsic character of relapses in Multiple Sclerosis. BMC Syst. Biol. 2011;5doi: 10.1186/1752-0509-5-114. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
  116. ↑ Jolivet R., Coggan J.S., Allaman I., Magistretti P.J. Multi-timescale modeling of activity-dependent metabolic coupling in the neuron-glia-vasculature ensemble. PLoS Comput. Biol. 2015;11:e1004036. doi: 10.1371/journal.pcbi.1004036. [PMC free article] [PubMed] [CrossRef]
  117. ↑ Zeis T., Allaman I., Gentner M., Schroder K., Tschopp J., Magistretti P.J., Schaeren-Wiemers N. Metabolic gene expression changes in astrocytes in Multiple Sclerosis cerebral cortex are indicative of immune-mediated signaling. Brain Behav. Immun. 2015;48:315–325. doi: 10.1016/j.bbi.2015.04.013.[PubMed] [CrossRef] [Google Scholar]
Retrieved from "https://www.masticationpedia.org/index.php?title=Dynamique_physiologique_dans_les_maladies_démyélinisantes_:_démêler_les_relations_complexes_grâce_à_la_modélisation_informatique&oldid=15802"