Masticationpedia

Store:QLMde02

Store Discussion
Revision as of 15:44, 9 November 2022 by Gianfranco (talk | contribs) (Created page with "== Introduction == The standard mathematical methods were originally developed to serve classical physics. The real analysis served as the mathematical basis of Newtonian mechanics (Newton, 1687)<ref>{{cita libro | autore = Newton Isaac | titolo = Philosophiae naturalis principia mathematica | url = https://archive.org/details/bub_gb_6EqxPav3vIsC | volume = | opera = | anno = 1687 | editore = Benjamin Motte | città = London UK | ISBN = | DOI = | PMID =...")
(diff) ← Older revision | Latest revision (diff) | Newer revision → (diff)
Go to top

Introduction

The standard mathematical methods were originally developed to serve classical physics. The real analysis served as the mathematical basis of Newtonian mechanics (Newton, 1687)[1] (and later Hamiltonian formalism); classical statistical mechanics stimulated the measure-theoretic approach to probability theory, formalized in Kolmogorov’s axiomatics (Kolmogorov, 1933)[2]. However, behavior of biological systems differ essentially from behavior of mechanical systems, say rigid bodies, gas molecules, or fluids. Therefore, although the “classical mathematics” still plays the crucial role in biological modeling, it seems that it cannot fully describe the rich complexity of biosystems and peculiarities of their behavior — as compared with mechanical systems. New mathematical methods for modeling biosystems are on demand.(a,b)

In this paper, we present the applications of the mathematical formalism of quantum mechanics and its methodology to modeling biosystems’ behavior.(c) The recent years were characterized by explosion of interest to applications of quantum theory outside of physics, especially in cognitive psychology, decision making, information processing in the brain, molecular biology, genetics and epigenetics, and evolution theory.4 We call the corresponding models quantum-like. They are not directed to micro-level modeling of real quantum physical processes in biosystems, say in cells or brains (cf. with biological applications of genuine quantum physical theory Penrose 1989,[3] Umezawa 1993,[4] Hameroff 1994,[5] Vitiello 1995,[6] Vitiello 2001,[7] Arndt et al., 2009,[8] Bernroider and Summhammer 2012,[9] Bernroider 2017[10]). Quantum-like modeling works from the viewpoint to quantum theory as a measurement theory. This is the original Bohr’s viewpoint that led to the Copenhagen interpretation of quantum mechanics (see Plotnitsky, 2009[11] for detailed and clear presentation of Bohr’s views). One of the main bio-specialties is consideration of self-measurements that biosystems perform on themselves. In our modeling, the ability to perform self-measurements is considered as the basic feature of biological functions (see Section 8.2 and paper Khrennikov et al., 2018[12]).

Quantum-like models (Khrennikov, 2004b[13]) reflect the features of biological processes that naturally match the quantum formalism. In such modeling, it is useful to explore quantum information theory, which can be applied not just to the micro-world of quantum systems. Generally, systems processing information in the quantum-like manner need not be quantum physical systems; in particular, they can be macroscopic biosystems. Surprisingly, the same mathematical theory can be applied at all biological scales: from proteins, cells and brains to humans and ecosystems; we can speak about quantum information biology (Asano et al., 2015a[14]).

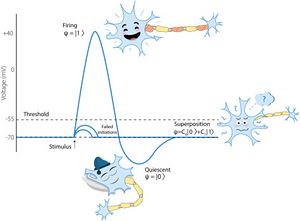
In quantum-like modeling, quantum theory is considered as calculus for prediction and transformation of probabilities. Quantum probability (QP) calculus (Section 2) differs essentially from classical probability (CP) calculus based on Kolmogorov’s axiomatics (Kolmogorov, 1933[15]). In CP, states of random systems are represented by probability measures and observables by random variables; in QP, states of random systems are represented by normalized vectors in a complex Hilbert space (pure states) or generally by density operators (mixed states).5 Superpositions represented by pure states are used to model uncertainty which is yet unresolved by a measurement. The use of superpositions in biology is illustrated by Fig. 1 (see Section 10 and paper Khrennikov et al., 2018[12] for the corresponding model). The QP-update resulting from an observation is based on the projection postulate or more general transformations of quantum states — in the framework of theory of quantum instruments (Davies and Lewis, 1970[16], Davies, 1976[17], Ozawa, 1984[18], Yuen, 1987[19], Ozawa, 1997[20], Ozawa, 2004[21], Okamura and Ozawa, 2016[22]) (Section 3).

Fig. 1. Illustration for quantum-like representation of uncertainty generated by neuron’s action potential (originally published in Khrennikov et al. (2018)).

We stress that quantum-like modeling elevates the role of convenience and simplicity of quantum representation of states and observables. (We pragmatically ignore the problem of interrelation of CP and QP.) In particular, the quantum state space has the linear structure and linear models are simpler. Transition from classical nonlinear dynamics of electrochemical processes in biosystems to quantum linear dynamics essentially speeds up the state-evolution (Section 8.4). However, in this framework “state” is the quantum information state of a biosystem used for processing of special quantum uncertainty (Section 8.2).

  1. ↑ Newton Isaac, «Philosophiae naturalis principia mathematica», Benjamin Motte, 1687, London UK». 
  2. ↑ Kolmogorov A.N.Grundbegriffe Der Wahrscheinlichkeitsrechnung. Springer-Verlag, Berlin (1933)
  3. ↑ Penrose R. The Emperor’S New Mind Oxford Univ. Press, New-York (1989)
  4. ↑ Umezawa H. Advanced Field Theory: Micro, Macro and Thermal Concepts AIP, New York (1993)
  5. ↑ Hameroff S. Quantum coherence in microtubules. a neural basis for emergent con- sciousness? J. Cons. Stud., 1 (1994)
  6. ↑ Vitiello G. Dissipation and memory capacity in the quantum brain model Internat. J. Modern Phys. B, 9 (1995), p. 973
  7. ↑ Vitiello G. My Double Unveiled: The Dissipative Quantum Model of Brain, Advances in Consciousness Research, John Benjamins Publishing Company(2001)
  8. ↑ Arndt M., Juffmann T., Vedral V. Quantum physics meets biology HFSP J., 3 (6) (2009), pp. 386-400, 10.2976/1.3244985
  9. ↑ Bernroider G., Summhammer J. Can quantum entanglement between ion transition states effect action potential initiation? Cogn. Comput., 4 (2012), pp. 29-37
  10. ↑ Bernroider G. Neuroecology: Modeling neural systems and environments, from the quantum to the classical level and the question of consciousness J. Adv. Neurosci. Res., 4 (2017), pp. 1-9
  11. ↑ Plotnitsky A. Epistemology and Probability: Bohr, Heisenberg, SchrÖdinger and the Nature of Quantum-Theoretical Thinking Springer, Berlin, Germany; New York, NY, USA (2009
  12. ↑ 12.0 12.1 Khrennikov A., Basieva I., PothosE.M., Yamato I. Quantum Probability in Decision Making from Quantum Information Representation of Neuronal States, Sci. Rep., 8 (2018), Article 16225
  13. ↑ Khrennikov A. On quantum-like probabilistic structure of mental information Open Syst. Inf. Dyn., 11 (3) (2004), pp. 267-275
  14. ↑ Asano M., Basieva I., Khrennikov A., Ohya M., Tanaka Y., Yamato I. Quantum information biology: from information interpretation of quantum mechanics to applications in molecular biology and cognitive psychology Found. Phys., 45 (10) (2015), pp. 1362-1378
  15. ↑ Kolmogorov A.N. Grundbegriffe Der Wahrscheinlichkeitsrechnung Springer-Verlag, Berlin (1933)
  16. ↑ Davies E.B., Lewis J.T. An operational approach to quantum probability Comm. Math. Phys., 17 (1970), pp. 239-260
  17. ↑ Davies E.B. Quantum Theory of Open Systems. Academic Press, London (1976)
  18. ↑ Ozawa M. Quantum measuring processes for continuous observables J. Math. Phys., 25 (1984), pp. 79-87
  19. ↑ Yuen, H. P., 1987. Characterization and realization of general quantum measurements. M. Namiki and others (ed.) Proc. 2nd Int. Symp. Foundations of Quantum Mechanics, pp. 360–363.
  20. ↑ Ozawa M. An operational approach to quantum state reduction Ann. Phys., NY, 259 (1997), pp. 121-137
  21. ↑ Ozawa M. Uncertainty relations for noise and disturbance in generalized quantum measurements Ann. Phys., NY, 311 (2004), pp. 350-416
  22. ↑ Okamura K., Ozawa M. Measurement theory in local quantum physics J. Math. Phys., 57 (2016), Article 015209
Retrieved from "https://www.masticationpedia.org/index.php?title=Store:QLMde02&oldid=13925"