Introduction
Les méthodes mathématiques standard ont été développées à l'origine pour servir la physique classique. L'analyse réelle a servi de base mathématique à la mécanique newtonienne (Newton, 1687)[1] (et plus tard au formalisme hamiltonien) ; la mécanique statistique classique a stimulé l'approche théorique de la mesure de la théorie des probabilités, formalisée dans l'axiomatique de Kolmogorov (Kolmogorov, 1933).[2] Cependant, le comportement des systèmes biologiques diffère essentiellement du comportement des systèmes mécaniques, par exemple des corps rigides, des molécules de gaz ou des fluides. Par conséquent, bien que les «mathématiques classiques» jouent toujours le rôle crucial dans la modélisation biologique, il semble qu'elles ne puissent pas décrire pleinement la riche complexité des biosystèmes et les particularités de leur comportement - par rapport aux systèmes mécaniques. De nouvelles méthodes mathématiques de modélisation des biosystèmes sont en demande.(a,b)
Dans cet article, nous présentons les applications du formalisme mathématique de la mécanique quantique et de sa méthodologie à la modélisation du comportement des biosystèmes. (c) Les dernières années ont été caractérisées par une explosion d'intérêt pour les applications de la théorie quantique en dehors de la physique, en particulier en psychologie cognitive, la prise de décision, le traitement de l'information dans le cerveau, la biologie moléculaire, la génétique et l'épigénétique, et la théorie de l'évolution.4 Nous appelons les modèles correspondants de type quantique. Ils ne sont pas dirigés vers la modélisation au niveau micro des processus physiques quantiques réels dans les biosystèmes, disons dans les cellules ou les cerveaux (cf. avec les applications biologiques de la théorie physique quantique authentique Penrose 1989,[3] Umezawa 1993,[4] Hameroff 1994,[5] Vitiello 1995,[6] Vitiello 2001,[7] Arndt et al., 2009,[8] Bernroider et Summhammer 2012,[9] Bernroider 2017[10]). La modélisation de type quantique fonctionne du point de vue de la théorie quantique en tant que théorie de la mesure. C'est le point de vue original de Bohr qui a conduit à l'interprétation de Copenhague de la mécanique quantique (voir Plotnitsky, 2009[11] pour une présentation détaillée et claire des vues de Bohr). L'une des principales spécialités des biosystèmes est la prise en compte des auto-mesures que les biosystèmes effectuent sur eux-mêmes. Dans notre modélisation, la capacité à effectuer des auto-mesures est considérée comme la caractéristique de base des fonctions biologiques (voir la section 8.2 et l'article de Khrennikov et al., 2018[12]).
Les modèles de type quantique (Khrennikov, 2004b[13]) reflètent les caractéristiques des processus biologiques qui correspondent naturellement au formalisme quantique. Dans une telle modélisation, il est utile d'explorer la théorie de l'information quantique, qui peut être appliquée non seulement au micro-monde des systèmes quantiques. Généralement, les systèmes traitant l'information de manière quantique n'ont pas besoin d'être des systèmes physiques quantiques; en particulier, il peut s'agir de biosystèmes macroscopiques. Étonnamment, la même théorie mathématique peut être appliquée à toutes les échelles biologiques : des protéines, des cellules et des cerveaux aux humains et aux écosystèmes ; on peut parler de biologie de l'information quantique (Asano et al., 2015a[14]).
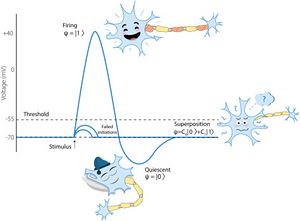
Dans la modélisation de type quantique, la théorie quantique est considérée comme un calcul pour la prédiction et la transformation des probabilités. Le calcul des probabilités quantiques (QP) (Section 2) diffère essentiellement du calcul classique des probabilités (CP) basé sur l'axiomatique de Kolmogorov (Kolmogorov, 1933[15]). En CP, les états des systèmes aléatoires sont représentés par des mesures de probabilité et les observables par des variables aléatoires ; dans QP, les états de systèmes aléatoires sont représentés par des vecteurs normalisés dans un espace de Hilbert complexe (états purs) ou généralement par des opérateurs de densité (états mixtes)5. Les superpositions représentées par des états purs sont utilisées pour modéliser l'incertitude qui n'est pas encore résolue par une mesure. L'utilisation des superpositions en biologie est illustrée par la Fig. 1 (voir Section 10 et article Khrennikov et al., 2018[12] pour le modèle correspondant). La mise à jour QP résultant d'une observation est basée sur le postulat de projection ou des transformations plus générales d'états quantiques — dans le cadre de la théorie des instruments quantiques (Davies et Lewis, 1970,[16] Davies, 1976,[17] Ozawa 1984,[18] Yuen, 1987,[19] Ozawa 1997,[20] Ozawa, 2004,[21] Okamura et Ozawa, 2016[22]) (Section 3).
Nous soulignons que la modélisation de type quantique élève le rôle de la commodité et de la simplicité de la représentation quantique des états et des observables. (Nous ignorons pragmatiquement le problème de l'interrelation de CP et QP.) En particulier, l'espace d'état quantique a la structure linéaire et les modèles linéaires sont plus simples. La transition de la dynamique non linéaire classique des processus électrochimiques dans les biosystèmes à la dynamique linéaire quantique accélère essentiellement l'évolution de l'état (Section 8.4). Cependant, dans ce cadre, «l'état» est l'état de l'information quantique d'un biosystème utilisé pour le traitement de l'incertitude quantique spéciale (section 8.2).
- ↑ Newton Isaac, «Philosophiae naturalis principia mathematica», Benjamin Motte, 1687, London UK».
- ↑ Kolmogorov A.N.Grundbegriffe Der Wahrscheinlichkeitsrechnung. Springer-Verlag, Berlin (1933)
- ↑ Penrose R. The Emperor’S New Mind Oxford Univ. Press, New-York (1989)
- ↑ Umezawa H. Advanced Field Theory: Micro, Macro and Thermal Concepts AIP, New York (1993)
- ↑ Hameroff S. Quantum coherence in microtubules. a neural basis for emergent con- sciousness? J. Cons. Stud., 1 (1994)
- ↑ Vitiello G. Dissipation and memory capacity in the quantum brain model Internat. J. Modern Phys. B, 9 (1995), p. 973
- ↑ Vitiello G. My Double Unveiled: The Dissipative Quantum Model of Brain, Advances in Consciousness Research, John Benjamins Publishing Company(2001)
- ↑ Arndt M., Juffmann T., Vedral V. Quantum physics meets biology HFSP J., 3 (6) (2009), pp. 386-400, 10.2976/1.3244985
- ↑ Bernroider G., Summhammer J. Can quantum entanglement between ion transition states effect action potential initiation? Cogn. Comput., 4 (2012), pp. 29-37
- ↑ Bernroider G. Neuroecology: Modeling neural systems and environments, from the quantum to the classical level and the question of consciousness J. Adv. Neurosci. Res., 4 (2017), pp. 1-9
- ↑ Plotnitsky A. Epistemology and Probability: Bohr, Heisenberg, SchrÖdinger and the Nature of Quantum-Theoretical Thinking Springer, Berlin, Germany; New York, NY, USA (2009
- ↑ 12.0 12.1 Khrennikov A., Basieva I., PothosE.M., Yamato I. Quantum Probability in Decision Making from Quantum Information Representation of Neuronal States, Sci. Rep., 8 (2018), Article 16225
- ↑ Khrennikov A. On quantum-like probabilistic structure of mental information Open Syst. Inf. Dyn., 11 (3) (2004), pp. 267-275
- ↑ Asano M., Basieva I., Khrennikov A., Ohya M., Tanaka Y., Yamato I. Quantum information biology: from information interpretation of quantum mechanics to applications in molecular biology and cognitive psychology Found. Phys., 45 (10) (2015), pp. 1362-1378
- ↑ Kolmogorov A.N. Grundbegriffe Der Wahrscheinlichkeitsrechnung Springer-Verlag, Berlin (1933)
- ↑ Davies E.B., Lewis J.T. An operational approach to quantum probability Comm. Math. Phys., 17 (1970), pp. 239-260
- ↑ Davies E.B. Quantum Theory of Open Systems. Academic Press, London (1976)
- ↑ Ozawa M. Quantum measuring processes for continuous observables J. Math. Phys., 25 (1984), pp. 79-87
- ↑ Yuen, H. P., 1987. Characterization and realization of general quantum measurements. M. Namiki and others (ed.) Proc. 2nd Int. Symp. Foundations of Quantum Mechanics, pp. 360–363.
- ↑ Ozawa M. An operational approach to quantum state reduction Ann. Phys., NY, 259 (1997), pp. 121-137
- ↑ Ozawa M. Uncertainty relations for noise and disturbance in generalized quantum measurements Ann. Phys., NY, 311 (2004), pp. 350-416
- ↑ Okamura K., Ozawa M. Measurement theory in local quantum physics J. Math. Phys., 57 (2016), Article 015209