Store:FLfr05

Ensemble fuzzy${\tilde {A}}$ et membership function $\mu _{\displaystyle {\tilde {A}}}(x)$

Nous choisissons - comme formalisme - de représenter un ensemble flou avec le 'tilde':${\tilde {A}}$. Un ensemble flou est un ensemble où les éléments ont un « degré » d'appartenance (conformément à la logique floue) : certains peuvent être inclus dans l'ensemble à 100 %, d'autres dans des pourcentages inférieurs.

Pour représenter mathématiquement ce degré d'appartenance, on utilise la fonction $\mu _{\displaystyle {\tilde {A}}}(x)$ appelée 'Membership Function'. La fonction $\mu _{\displaystyle {\tilde {A}}}(x)$ est une fonction continue définie dans l'intervalle $[0;1]$ où elle vaut :

• $\mu _{\tilde {A}}(x)=1\rightarrow$si $x$ est totalement contenu dans $A$ (ces points sont appelés 'noyau', ils indiquent des valeurs de prédicat plausibles).
• $\mu _{\tilde {A}}(x)=0\rightarrow$si $x$ n'est pas contenu dans$A$
• $0<\mu _{\tilde {A}}(x)<1\;\rightarrow$si $x$ est partiellement contenu dans $A$ (ces points sont appelés 'support', ils indiquent les valeurs possibles des prédicats).

La représentation graphique de la fonction $\mu _{\displaystyle {\tilde {A}}}(x)$ peut être varié; de ceux avec des lignes linéaires (triangulaires, trapézoïdales) à ceux en forme de cloches ou de "S" (sigmoïdal) comme représenté sur la figure 1, qui contient tout le concept graphique de la fonction d'appartenance.

Figure 1: Types de graphiques pour la fonction d'appartenance.

L'ensemble support d'un ensemble flou est défini comme la zone dans laquelle résulte le degré d'appartenance$0<\mu _{\tilde {A}}(x)<1$; d'autre part, le noyau est défini comme la zone dans laquelle le degré d'appartenance prend la valeur $\mu _{\tilde {A}}(x)=1$.

Le 'Support set' représente les valeurs du prédicat jugées possibles, tandis que le 'core' représente celles jugées les plus plausibles.

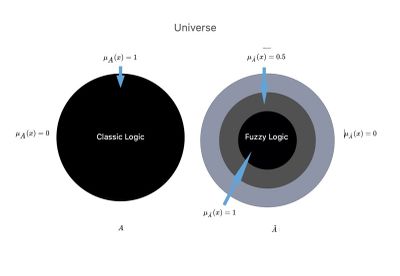
Si ${A}$ représentait un ensemble au sens ordinaire du terme ou de la logique du langage classique décrit précédemment, sa fonction d'appartenance ne pourrait prendre que les valeurs $1$ ou $0$,$\mu _{\displaystyle {A}}(x)=1\;\lor \;\mu _{\displaystyle {A}}(x)=0$ selon que l'élément $x$ appartient ou non au tout considéré. La figure 2 montre une représentation graphique du concept net (rigidement défini) ou flou d'appartenance, qui rappelle clairement les considérations de Smuts.

Revenons au cas particulier de notre Mary Poppins, dans laquelle nous voyons un décalage entre les affirmations du dentiste et du neurologue et nous cherchons une comparaison entre la logique classique et la logique floue :

Figure 2: Representation of the comparison between a classical and fuzzy ensemble.

Figure 2 : Imaginons l'univers scientifique $U$ dans lequel il y a deux mondes ou contextes parallèles, ${A}$ et ${\tilde {A}}$.

${A}=$ Dans le contexte scientifique, le soi-disant « croustillant », et nous l'avons converti dans la logique du langage classique, dans lequel le médecin dispose d'une information de base scientifique absolue $KB$ avec une ligne de démarcation claire que nous avons nommée $KB_{c}$.

${\tilde {A}}=$ Dans un autre contexte scientifique appelé « logique floue », et dans lequel il existe une union entre le sous-ensemble ${A}$ en${\tilde {A}}$ que l'on peut aller jusqu'à dire : union entre $KB_{c}$.

On remarquera remarquablement les déductions suivantes :

• Logique classique dans le contexte dentaire ${A}$ dans laquelle seul un processus logique donnant comme résultat $\mu _{\displaystyle {A}}(x)=1$ sera possible, ou $\mu _{\displaystyle {A}}(x)=0$ étant la plage de données $D=\{\delta _{1},\dots ,\delta _{4}\}$ réduite aux connaissances de base $KB$ dans l'ensemble ${A}$. Cela signifie qu'en dehors du monde dentaire, il existe un vide et que le terme de la théorie des ensembles s'écrit précisément $\mu _{\displaystyle {A}}(x)=0$ et qui est synonyme d'une gamme élevée de :

«Differential diagnostic error»

• Logique floue dans un contexte dentaire ${\tilde {A}}$ dans lequel ils sont représentés au-delà des connaissances de base $KB$ du contexte dentaire également celles partiellement acquises du monde neurophysiologique $0<\mu _{\tilde {A}}(x)<1$ auront la prérogative de rendre un résultat $\mu _{\tilde {A}}(x)=1$ et un résultat $0<\mu _{\tilde {A}}(x)<1$ à cause des connaissances de base $KB$ qui à ce point est représenté par l'union de $KB_{c}$ contextes dentaire et neurologique. Le résultat de cette mise en œuvre scientifique et clinique de la dentisterie permettrait une.
  «Réduction de l'erreur de diagnostic différentiel»