Difference between revisions of "Store:ACincisivo"
| Line 3: | Line 3: | ||
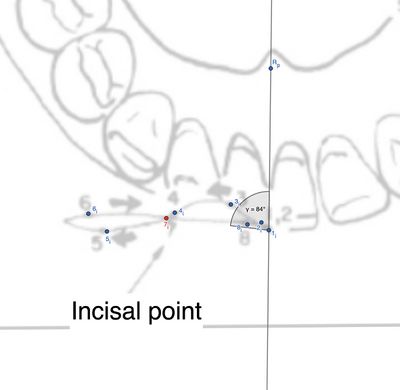
Il paragrafo caricato descrive un'analisi matematica dei movimenti articolari dell'incisivo sul lato lavorante. Utilizzando le coordinate di tre punti nello spazio 2D (P1, P7 e H₃), vengono calcolate le distanze lineari tra i punti, oltre all'angolo tra i segmenti che collegano questi punti. | Il paragrafo caricato descrive un'analisi matematica dei movimenti articolari dell'incisivo sul lato lavorante. Utilizzando le coordinate di tre punti nello spazio 2D (P1, P7 e H₃), vengono calcolate le distanze lineari tra i punti, oltre all'angolo tra i segmenti che collegano questi punti. | ||
<br /> | <br /> | ||
{| | {| | ||
! colspan=" | ! colspan="5" |Tabella 3 | ||
|- | |- | ||
! | !Tracciato masticatorio | ||
!Markers | |||
!Distanza (mm) | !Distanza (mm) | ||
!Direzione in X | !Direzione in X | ||
| Line 15: | Line 15: | ||
!Direzione | !Direzione | ||
dinamica | dinamica | ||
(Y-latero-mediale) | (Y-latero-mediale) | ||
|- | |- | ||
| rowspan="7" |[[File:Incisal angle.jpg|400x400px|Figura 3: |center]]'''Figura 3:''' | |||
|2 | |2 | ||
|2.34 | |2.34 | ||
Revision as of 18:53, 8 December 2024
Incisal
Il paragrafo caricato descrive un'analisi matematica dei movimenti articolari dell'incisivo sul lato lavorante. Utilizzando le coordinate di tre punti nello spazio 2D (P1, P7 e H₃), vengono calcolate le distanze lineari tra i punti, oltre all'angolo tra i segmenti che collegano questi punti.
| Tabella 3 | ||||
|---|---|---|---|---|
| Tracciato masticatorio | Markers | Distanza (mm) | Direzione in X
(antero-posteriore) |
Direzione
dinamica (Y-latero-mediale) |
| Figura 3: | 2 | 2.34 | Indietro | Lateralizzazione |
| 3 | 4.57 | Indietro | Lateralizzazione | |
| 4 | 10.96 | Indietro | Lateralizzazione | |
| 5 | 20.28 | Indietro | Lateralizzazione | |
| 6 | 21.80 | Indietro | Inversione | |
| 7* | 13.84 | Indietro | Medializzazione | |
| 8 | 2.64 | Indietro | Medializzazione | |
Per quanto riguarda i tracciati nell'area dell'incisivo tra il punto e la distanza risulta essere di 13.84 mm con un angolo . Per approfondimenti di calcolo vedi ![]() Coordinate dei punti: , , .Il vettore tra e è: .Il vettore tra e è: .Il prodotto scalare tra i vettori è calcolato come: .Le norme dei vettori sono: e .Il coseno dell'angolo tra i vettori è dato da: .Infine, l'angolo è: .
Coordinate dei punti: , , .Il vettore tra e è: .Il vettore tra e è: .Il prodotto scalare tra i vettori è calcolato come: .Le norme dei vettori sono: e .Il coseno dell'angolo tra i vettori è dato da: .Infine, l'angolo è: .