Difference between revisions of "Store:ACincisivo"

Revision as of 19:01, 28 October 2024

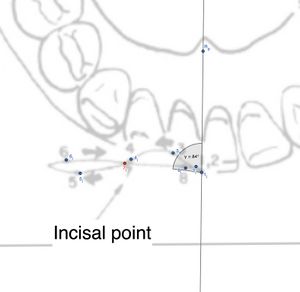
Incisal

Il paragrafo caricato descrive un'analisi matematica dei movimenti articolari dell'incisivo sul lato lavorante. Utilizzando le coordinate di tre punti nello spazio 2D (P1, P7 e H₃), vengono calcolate le distanze lineari tra i punti, oltre all'angolo tra i segmenti che collegano questi punti.

Figura

Punto	Distanza (pixel)	Distanza (mm)	Direzione in X (antero-posteriore)	Direzione in Y (latero-mediale)
2	23.4	2.34	Indietro	Laterale
3	45.65	4.57	Indietro	Laterale
4	109.56	10.96	Indietro	Laterale
5	202.77	20.28	Indietro	Laterale
6	218.02	21.80	Indietro	Laterale
7	138.42	13.84	Indietro	Laterale
8	26.41	2.64	Indietro	Laterale

Dalla tabella, innanzitutto, dobbiamo calcolare i vettori Descrizione focalizzata dell'analisi matematica dei punti Punti e coordinate coinvolte Nel contesto della nostra analisi, abbiamo tre punti nello spazio 2D di interesse: * Coordinate $P1_{i}$ del punto 1 dell'incisivo sul lato lavorante: $(631.5,-1151.8)$ * Coordinate $P7_{i}$ del punto 7 dell'incisivo sul lato lavorante: $(509.6,-1139.9)$ * Coordinate $H3_{i}$ del punto di riferimento dell'incisivo sul lato lavorante: $(634.2,-921)$ Questi punti rappresentano posizioni specifiche all'interno di un sistema articolare che stiamo studiando. L'obiettivo è calcolare l'angolo tra il segmento che unisce i punti $P1_{i}$ e $P7_{i}$ , e il segmento che unisce i punti $P1_{i}$ e $H3_{i}$ . Questo tipo di analisi è comune nella modellazione di movimenti articolari per comprendere come si muovono i segmenti di un sistema rispetto a un punto di riferimento, come nel caso di un sistema masticatorio. ====Iter matematico per il calcolo dell'angolo==== L'angolo tra due segmenti può essere calcolato utilizzando la **trigonometria vettoriale** e, in particolare, il **prodotto scalare**. Questo metodo è utile per determinare la relazione angolare tra due movimenti distinti nello spazio. ====1. Definizione dei vettori==== Dobbiamo calcolare i vettori che rappresentano i segmenti tra i punti: * Il vettore tra il punto $P1_{i}$ e il punto $P7_{i}$ : ${\vec {AB}}=P7_{i}-P1_{i}=(509.6,-1139.9)-(631.5,-1151.8)=(-121.9,11.9)$ * Il vettore tra il punto 1_Lm e il punto H₃: ${\vec {AC}}=H3_{i}-P1_{i}=(634.2,-921)-(631.5,-1151.8)=(2.7,230.8)$ ====2. Prodotto scalare==== Il **prodotto scalare** tra i vettori ${\vec {AB}}$ e ${\vec {AC}}$ è dato dalla formula: ${\vec {AB}}\cdot {\vec {AC}}=AB_{x}\cdot AC_{x}+AB_{y}\cdot AC_{y}$ , e sostituendo i valori calcolati: ${\vec {AB}}\cdot {\vec {AC}}=(-121.9)\cdot (2.7)+(11.9)\cdot (230.8)=-329.13+2746.52=2417.39$ ====3. Calcolo delle norme==== Le norme (lunghezze) dei due vettori sono calcolate con la formula della lunghezza del vettore: $|{\vec {AB}}|={\sqrt {AB_{x}^{2}+AB_{y}^{2}}}={\sqrt {(-121.9)^{2}+(11.9)^{2}}}={\sqrt {15004.02}}\approx 122.48$ e $|{\vec {AC}}|={\sqrt {AC_{x}^{2}+AC_{y}^{2}}}={\sqrt {53275.93}}\approx 230.85$ ====4. Calcolo dell'angolo==== Usando la formula per il coseno dell'angolo tra i due vettori: $\cos(\theta )={\frac {{\vec {AB}}\cdot {\vec {AC}}}{|{\vec {AB}}|\cdot |{\vec {AC}}|}}$ , otteniamo $\cos(\theta )={\frac {2417.39}{28252.53}}\approx 0.0856$ . Infine, l'angolo $\theta$ è calcolato tramite la funzione arcoseno: $\theta =\arccos(0.0856)\approx 85.09^{\circ }$ . ====Motivo dell'analisi==== L'obiettivo dell'analisi è determinare l'angolo tra due movimenti all'interno di un sistema articolare, in particolare nell'area di studio della cinematica masticatoria. La comprensione di questi angoli ci consente di valutare la dinamica mandibolare, modellare la biomeccanica del sistema masticatorio e confrontare con angoli standard. Questo calcolo è fondamentale per fornire una descrizione matematica precisa della cinetica mandibolare e per migliorare la modellazione biomeccanica di strutture orofacciali, cruciali per la diagnosi e l'intervento clinico. che rappresentano i segmenti tra i punti:

@@ Line 57: / Line 57: @@
 |Laterale
 |}
-<br />Dalla tabella, innanzitutto, dobbiamo calcolare i vettori{{Tooltip|2=<nowiki>"Descrizione focalizzata dell'analisi matematica dei punti: Nel contesto della nostra analisi, abbiamo tre punti nello spazio 2D che ci interessano: Coordinate P1_{i} del punto 1 dell'incisivo sul lato lavorante: (631.5,-1151.8), Coordinate P7_{i} del punto 7 dell'incisivo sul lato lavorante: (509.6,-1139.9), Coordinate H3_{i} del punto di riferimento dell'incisivo sul lato lavorante: (634.2,-921). Questi punti rappresentano tre posizioni specifiche all'interno di un sistema articolare che stiamo studiando, con l'obiettivo di calcolare l'angolo tra il segmento che unisce i punti P1_{i} e P7_{i} e il segmento che unisce i punti P1_{i} e H3_{i}. Questo tipo di analisi è comune nella modellazione di movimenti articolari per comprendere come si muovono i segmenti di un sistema rispetto a un punto di riferimento, come nel caso di un sistema masticatorio. Iter matematico per il calcolo dell'angolo: L'angolo tra due segmenti può essere calcolato utilizzando la trigonometria vettoriale e, in particolare, il prodotto scalare. Questo metodo è utile quando vogliamo determinare la relazione angolare tra due movimenti distinti nello spazio. Definizione dei vettori: Innanzitutto, dobbiamo calcolare i vettori che rappresentano i segmenti tra i punti: Il vettore tra il punto P1_{i} e il punto P7_{i}: AB = P7_{i} - P1_{i} = (509.6, -1139.9) - (631.5, -1151.8) = (-121.9, 11.9), Il vettore tra il punto 1Lm e il punto H₃: AC = H3_{i} - P1_{i} = (634.2, -921) - (631.5, -1151.8) = (2.7, 230.8). Prodotto scalare: Il prodotto scalare tra due vettori AB e AC è dato dalla formula: AB ⋅ AC = AB_x ⋅ AC_x + AB_y ⋅ AC_y. Sostituendo i valori calcolati: AB ⋅ AC = (-121.9) ⋅ (2.7) + (11.9) ⋅ (230.8) = -329.13 + 2746.52 = 2417.39. Calcolo delle norme: Le norme (lunghezze) dei due vettori sono calcolate con la formula della lunghezza del vettore: |AB| = √(AB_x^2 + AB_y^2) = √((-121.9)^2 + (11.9)^2) = √(15004.02) ≈ 122.48, |AC| = √(AC_x^2 + AC_y^2) = √((2.7)^2 + (230.8)^2) = √(53275.93) ≈ 230.85. Calcolo dell'angolo: Ora possiamo usare la formula per il coseno dell'angolo tra i due vettori: cos(θ) = AB ⋅ AC / (|AB| ⋅ |AC|), e sostituendo i valori: cos(θ) = 2417.39 / 28252.53 ≈ 0.0856. Infine, l'angolo θ è calcolato tramite la funzione arcoseno: θ ≈ 85.09°. Motivo dell'analisi: L'obiettivo dell'analisi è determinare l'angolo tra due movimenti all'interno di un sistema articolare, in particolare nell'area di studio della cinematica masticatoria. La comprensione di questi angoli ci consente di: Valutare la dinamica mandibolare, Modellare la biomeccanica del sistema masticatorio, Confrontare con angoli standard. Questo calcolo è fondamentale per fornire una descrizione matematica precisa della cinetica mandibolare e per migliorare la modellazione biomeccanica di strutture orofacciali, cruciali per la diagnosi e l'intervento clinico."|2}}</nowiki>}} che rappresentano i segmenti tra i punti:
+<br />Dalla tabella, innanzitutto, dobbiamo calcolare i vettori{{Tooltip|2=Descrizione focalizzata dell'analisi matematica dei punti '''Punti e coordinate coinvolte'''  Nel contesto della nostra analisi, abbiamo tre punti nello spazio 2D di interesse: * Coordinate <math>P1_{i}</math> del punto 1 dell'incisivo sul lato lavorante: <math>(631.5, -1151.8)</math> * Coordinate <math>P7_{i}</math> del punto 7 dell'incisivo sul lato lavorante: <math>(509.6, -1139.9)</math> * Coordinate <math>H3_{i}</math> del punto di riferimento dell'incisivo sul lato lavorante: <math>(634.2, -921)</math> Questi punti rappresentano posizioni specifiche all'interno di un sistema articolare che stiamo studiando. L'obiettivo è calcolare l'angolo tra il segmento che unisce i punti <math>P1_{i}</math> e <math>P7_{i}</math>, e il segmento che unisce i punti <math>P1_{i}</math> e <math>H3_{i}</math>. Questo tipo di analisi è comune nella modellazione di movimenti articolari per comprendere come si muovono i segmenti di un sistema rispetto a un punto di riferimento, come nel caso di un sistema masticatorio. ====Iter matematico per il calcolo dell'angolo==== L'angolo tra due segmenti può essere calcolato utilizzando la **trigonometria vettoriale** e, in particolare, il **prodotto scalare**. Questo metodo è utile per determinare la relazione angolare tra due movimenti distinti nello spazio. ====1. Definizione dei vettori==== Dobbiamo calcolare i vettori che rappresentano i segmenti tra i punti: * Il vettore tra il punto <math>P1_{i}</math> e il punto <math>P7_{i}</math>: <math>\vec{AB} = P7_{i} - P1_{i} = (509.6, -1139.9) - (631.5, -1151.8) = (-121.9, 11.9)</math> * Il vettore tra il punto 1<sub>Lm</sub> e il punto H₃: <math>\vec{AC} = H3_{i} - P1_{i} = (634.2, -921) - (631.5, -1151.8) = (2.7, 230.8)</math> ====2. Prodotto scalare==== Il **prodotto scalare** tra i vettori <math>\vec{AB}</math> e <math>\vec{AC}</math> è dato dalla formula: <math>\vec{AB} \cdot \vec{AC} = AB_x \cdot AC_x + AB_y \cdot AC_y</math>, e sostituendo i valori calcolati: <math>\vec{AB} \cdot \vec{AC} = (-121.9) \cdot (2.7) + (11.9) \cdot (230.8) = -329.13 + 2746.52 = 2417.39</math> ====3. Calcolo delle norme==== Le norme (lunghezze) dei due vettori sono calcolate con la formula della lunghezza del vettore: <math>|\vec{AB}| = \sqrt{AB_x^2 + AB_y^2} = \sqrt{(-121.9)^2 + (11.9)^2} = \sqrt{15004.02} \approx 122.48</math> e <math>|\vec{AC}| = \sqrt{AC_x^2 + AC_y^2} = \sqrt{53275.93} \approx 230.85</math> ====4. Calcolo dell'angolo==== Usando la formula per il coseno dell'angolo tra i due vettori: <math>\cos(\theta) = \frac{\vec{AB} \cdot \vec{AC}}{|\vec{AB}| \cdot |\vec{AC}|}</math>, otteniamo <math>\cos(\theta) = \frac{2417.39}{28252.53} \approx 0.0856</math>. Infine, l'angolo <math>\theta</math> è calcolato tramite la funzione arcoseno: <math>\theta = \arccos(0.0856) \approx 85.09^\circ</math>. ====Motivo dell'analisi==== L'obiettivo dell'analisi è determinare l'angolo tra due movimenti all'interno di un sistema articolare, in particolare nell'area di studio della cinematica masticatoria. La comprensione di questi angoli ci consente di valutare la dinamica mandibolare, modellare la biomeccanica del sistema masticatorio e confrontare con angoli standard. Questo calcolo è fondamentale per fornire una descrizione matematica precisa della cinetica mandibolare e per migliorare la modellazione biomeccanica di strutture orofacciali, cruciali per la diagnosi e l'intervento clinico.}} che rappresentano i segmenti tra i punti:
-'''Prodotto scalare'''Il **prodotto scalare** tra due vettori <math>\vec{AB}</math> e <math>\vec{AC}</math> è dato dalla formula:<math>\vec{AB} \cdot \vec{AC} = AB_x \cdot AC_x + AB_y \cdot AC_y</math>Sostituendo i valori calcolati:<math>\vec{AB} \cdot \vec{AC} = (-121.9) \cdot (2.7) + (11.9) \cdot (230.8) = -329.13 + 2746.52 = 2417.39</math>'''Calcolo delle norme'''Le norme (lunghezze) dei due vettori sono calcolate con la formula della lunghezza del vettore:<math>|\vec{AB}| = \sqrt{AB_x^2 + AB_y^2} = \sqrt{(-121.9)^2 + (11.9)^2} = \sqrt{14862.41 + 141.61} = \sqrt{15004.02} \approx 122.48</math<math>|\vec{AC}| = \sqrt{AC_x^2 + AC_y^2} = \sqrt{(2.7)^2 + (230.8)^2} = \sqrt{7.29 + 53268.64} = \sqrt{53275.93} \approx 230.85</math>
-'''Calcolo dell'angolo'''Ora possiamo usare la formula per il coseno dell'angolo tra i due vettori:<math>\cos(\theta) = \frac{\vec{AB} \cdot \vec{AC}}{|\vec{AB}| \cdot |\vec{AC}|}</math>Sostituendo i valori:<math>\cos(\theta) = \frac{2417.39}{122.48 \cdot 230.85} = \frac{2417.39}{28252.53} \approx 0.0856</math>Infine, l'angolo \(\theta\) è calcolato tramite la funzione arcoseno:<math>\theta = \arccos(0.0856) \approx 85.09^\circ</math> Motivo dell'analisi'''L'obiettivo dell'analisi è determinare l'angolo tra due movimenti all'interno di un sistema articolare, in particolare nell'area di studio della cinematica masticatoria. La comprensione di questi angoli ci consente di:'''Valutare la dinamica mandibolare: Calcolare gli angoli tra i segmenti mandibolari può fornire informazioni essenziali su come la mandibola si sposta durante il movimento, aiutando a descrivere i pattern del movimento articolare.'''Modellare la biomeccanica del sistema masticatorio''': Gli angoli tra i punti permettono di costruire modelli accurati che simulano il comportamento meccanico del sistema mandibolare, utilizzabili in applicazioni cliniche per diagnosi e trattamenti. '''Confrontare con angoli standard'''<nowiki>: Gli angoli misurati possono essere confrontati con valori normali o patologici per identificare eventuali alterazioni nei movimenti mandibolari che potrebbero indicare disturbi dell'articolazione temporomandibolare (ATM). Questo calcolo è fondamentale per fornire una descrizione matematica precisa della cinetica mandibolare e per migliorare la modellazione biomeccanica di strutture orofacciali, cruciali per la diagnosi e l'intervento clinico.}} le distanze lineari (in pixel e millimetri) mostrano un movimento generale "indietro" e "laterale". Il calcolo dettagliato dei vettori tra i punti, tramite prodotto scalare e norme, consente di determinare che l'angolo tra i segmenti è di </nowiki>'''85.09°'''.
-L'analisi aiuta a comprendere come i segmenti mandibolari si muovano rispetto a un punto di riferimento, con implicazioni per la modellazione biomeccanica della mandibola e la diagnosi di disturbi articolari.