Difference between revisions of "Dinamiche fisiologiche nelle malattie demielinizzanti: svelare relazioni complesse attraverso la modellazione al computer"
| Line 120: | Line 120: | ||
Soprattutto se abbinata agli esperimenti tradizionali, la modellazione computazionale è indispensabile per dare un senso a dati incoerenti e meccanismi complessi. Questi benefici sono esemplificati dall'applicazione di simulazioni in altri campi, come l'epilessia.<ref>Soltesz I., Staley K. Computational Neuroscience in Epilepsy. 1st ed. Elsevier; London, UK: 2008. [Google Scholar]</ref> Qui esaminiamo parte della storia della modellazione computazionale di assoni, conduttanze ioniche, fisiologia della mielina e demielinizzazione, sistema immunitario, mitocondri e altri fattori biologici che sono fondamentali per comprendere le malattie demielinizzanti. La nostra recensione non è esaustiva, ma fornirà un'ampia introduzione agli sforzi passati, presenti e futuri in questo settore. | Soprattutto se abbinata agli esperimenti tradizionali, la modellazione computazionale è indispensabile per dare un senso a dati incoerenti e meccanismi complessi. Questi benefici sono esemplificati dall'applicazione di simulazioni in altri campi, come l'epilessia.<ref>Soltesz I., Staley K. Computational Neuroscience in Epilepsy. 1st ed. Elsevier; London, UK: 2008. [Google Scholar]</ref> Qui esaminiamo parte della storia della modellazione computazionale di assoni, conduttanze ioniche, fisiologia della mielina e demielinizzazione, sistema immunitario, mitocondri e altri fattori biologici che sono fondamentali per comprendere le malattie demielinizzanti. La nostra recensione non è esaustiva, ma fornirà un'ampia introduzione agli sforzi passati, presenti e futuri in questo settore. | ||
==== | ==== Modellazione degli assoni ==== | ||
La modellazione computazionale degli assoni si è evoluta tassonomicamente, dai calamari ai tessuti dei mammiferi con un corrispondente aumento di sofisticazione. Il modello di Hodgkin e Huxley (HH), che ha fornito la prima spiegazione completa della generazione di AP, è stato derivato da esperimenti in assoni giganti non mielinizzati di calamari,,<ref>Hodgkin A.L., Huxley A.F. The components of membrane conductance in the giant axon of ''Loligo''. J. Physiol. 1952;116:473–496. doi: 10.1113/jphysiol.1952.sp004718. [PMC free article] [PubMed] [CrossRef] [Google Scholar]</ref><ref>Hodgkin A.L., Huxley A.F. Currents carried by sodium and potassium ions through the membrane of the giant axon of ''Loligo''. J. Physiol. 1952;116:449–472. doi: 10.1113/jphysiol.1952.sp004717. [PMC free article] [PubMed] </ref> ma questo primo modello ha dimostrato di essere uno strumento inestimabile da cui successivamente , si sono evoluti modelli più sofisticati di assoni mielinizzati. | |||
L'eterogeneità spaziale e biofisica conferita dall'aggiunta di mielina, e la conseguente formazione di nodi e regioni internodali, rappresenta un aumento significativo della complessità degli assoni. Il primo modello computazionale di un assone mielinizzato era un modello unidimensionale che faceva collassare la guaina mielinica nell'assolemma passivo sottostante, utilizzava una dimensione del passo spaziale uniforme per formare l'approssimazione discreta utilizzata nella soluzione numerica e impiegava una caratterizzazione HH della membrana nodale.<ref>Fitzhugh R. Computation of impulse initiation and saltatory conduction in a myelinated nerve fiber. Biophys. J. 1962;2:11–21. doi: 10.1016/S0006-3495(62)86837-4. [PMC free article] [PubMed] [CrossRef] [Google Scholar]</ref> Goldman & Albus<ref>Goldman L., Albus J.S. Computation of impulse conduction in myelinated fibers; theoretical basis of the velocity-diameter relation. Biophys. J. 1968;8:596–607. doi: 10.1016/S0006-3495(68)86510-5. [PMC free article][PubMed] [CrossRef] [Google Scholar]</ref> hanno modificato questo modello per includere una descrizione della membrana nodale derivata dai dati sperimentali sulle fibre nervose mielinizzate di Xenopus laevis come determinato da Frankenhaeuser & Huxley.<ref>Frankenhaeuser B., Huxley A.F. The action potential in the myelinated nerve fiber of ''Xenopus'' ''laevis'' as computed on the basis of voltage clamp data. J. Physiol. 1964;171:302–315. doi: 10.1113/jphysiol.1964.sp007378.[PMC free article] [PubMed] [CrossRef] [Google Scholar]</ref> Studi successivi hanno utilizzato la stessa forma base per il modello con alcune varianti per la rappresentazione dell'axolemma. <ref name=":2" /><ref>Smith R.S., Koles Z.J. Myelinated nerve fibers: Computed effect of myelin thickness on conduction velocity. Am. J. Physiol. 1970;219:1256–1258.[PubMed] [Google Scholar]</ref><ref>Hutchinson N.A., Koles Z.J., Smith R.S. Conduction velocity in myelinated nerve fibres of ''Xenopus'' ''laevis''. J. Physiol. 1970;208:279–289. doi: 10.1113/jphysiol.1970.sp009119. [PMC free article] [PubMed] [CrossRef] [Google Scholar]</ref><ref>Koles Z.J., Rasminsky M. A computer simulation of conduction in demyelinated nerve fibres. J. Physiol. 1972;227:351–364. doi: 10.1113/jphysiol.1972.sp010036. [PMC free article] [PubMed] [CrossRef] [Google Scholar]</ref><ref>Hardy W.L. Propagation speed in myelinated nerve. II. Theoretical dependence on external Na and on temperature. Biophys. J. 1973;13:1071–1089. doi: 10.1016/S0006-3495(73)86046-1. [PMC free article] [PubMed] [CrossRef] [Google Scholar]</ref><ref>Schauf C.L., Davis F.A. Impulse conduction in multiple sclerosis: A theoretical basis for modification by temperature and pharmacological agents. J. Neurol. Neurosurg. Psychiatry. 1974;37:152–161. doi: 10.1136/jnnp.37.2.152.[PMC free article] [PubMed] [CrossRef] [Google Scholar]</ref><ref>Brill M.H., Waxman S.G., Moore J.W., Joyner R.W. Conduction velocity and spike configuration in myelinated fibres: Computed dependence on internode distance. J. Neurol. Neurosurg. Psychiatry. 1977;40:769–774. doi: 10.1136/jnnp.40.8.769. [PMC free article] [PubMed] [CrossRef] [Google Scholar]</ref><ref>Waxman S.G., Brill M.H. Conduction through demyelinated plaques in multiple sclerosis: Computer simulations of facilitation by short internodes. J. Neurol. Neurosurg. Psychiatry. 1978;41:408–416. doi: 10.1136/jnnp.41.5.408.[PMC free article] [PubMed] [CrossRef] [Google Scholar]</ref><ref>Wood S.L., Waxman S.G., Kocsis J.D. Conduction of trans of impulses in uniform myelinated fibers: Computed dependence on stimulus frequency. Neuroscience. 1982;7:423–430. doi: 10.1016/0306-4522(82)90276-7. [PubMed] [CrossRef] [Google Scholar]</ref><ref>Goldfinger M.D. Computation of high safety factor impulse propagation at axonal branch points. Neuroreport. 2000;11:449–456. doi: 10.1097/00001756-200002280-00005. [PubMed] [CrossRef] [Google Scholar]</ref> Il modello a cavo singolo, che descrive l'assone e tutte le sue proprietà di conduttanza e capacità in un'equazione di cavo, ha dominato il campo fino ai giorni nostri nonostante l'introduzione di modelli a cavo doppio da parte di Blight.<ref name=":14">Blight A.R. Computer simulation of action potentials and afterpotentials in mammalian myelinated axons: The case for a lower resistance myelin sheath. Neuroscience. 1985;15:13–31. doi: 10.1016/0306-4522(85)90119-8. [PubMed] [CrossRef] [Google Scholar]</ref> Nei modelli a doppio cavo, l'axolemma internodale e la guaina mielinica sono rappresentati indipendentemente. Il modello a doppio cavo è stato ampliato da Halter e Clark<ref name=":15">Halter J.A., Clark J.W., Jr. A distributed-parameter model of the myelinated nerve fiber. J. Theor. Biol. 1991;148:345–382. doi: 10.1016/S0022-5193(05)80242-5. [PubMed] [CrossRef] [Google Scholar]</ref> per esplorare gli effetti della complessa geometria degli oligodendrociti del SNC (o cellule di Schwann nel caso del SNP). | |||
I modelli più recenti hanno anche migliorato le precedenti semplificazioni, tra cui la complessità anatomica del nodo di Ranvier, la distribuzione dei canali ionici nell'assone sotto la guaina mielinica, le diverse proprietà elettriche della guaina mielinica e dell'axolemma e la sistemazione del possibile flusso di corrente all'interno lo spazio periassonale. <ref name=":15" /><ref>Schwarz J.R., Eikhof G. Na currents and action potentials in rat myelinated nerve fibres at 20 and 37 °C. Pflugers Arch. 1987;409:569–577. doi: 10.1007/BF00584655. [PubMed] [CrossRef] [Google Scholar]</ref><ref name=":16">Stephanova D.I. Myelin as longitudinal conductor: A multi-layered model of the myelinated human motor nerve fibre. Biol. Cybern. 2001;84:301–308. doi: 10.1007/s004220000213. [PubMed] [CrossRef] [Google Scholar]</ref><ref name=":17">McIntyre C.C., Richardson A.G., Grill W.M. Modeling the excitability of mammalian nerve fibers: Influence of afterpotentials on the recovery cycle. J. Neurophysiol. 2002;87:995–1006. [PubMed] [Google Scholar]</ref><ref name=":18">Einziger P.D., Livshitz L.M., Mizrahi J. Generalized cable equation model for myelinated nerve fiber. IEEE Trans. Biomed. Eng. 2005;52:1632–1642. doi: 10.1109/TBME.2005.856031. [PubMed] [CrossRef] [Google Scholar]</ref> Le rappresentazioni anatomiche dell'area paranodale hanno consentito una valutazione più dettagliata degli effetti della lesione cerebrale traumatica (TBI) sugli assoni mielinizzati.<ref>Volman V., Ng L. Primary paranode demyelination modulates slowly developing axonal depolarization in a model of axonal injury. J. Neural Comput. 2014;37:439–457. [PubMed] [Google Scholar]</ref> Uno dei modelli anatomicamente più sofisticati include la rappresentazione della complessa struttura della guaina acquosa delle lamelle mieliniche come una serie di lamelle parallele interconnesse in un modello di nervi motori. <ref name=":6" /><ref name=":16" /> | |||
I modelli più recenti hanno anche considerato la distribuzione non uniforme dei canali ionici in tutto l'assone <ref name=":4" /><ref>Stephanova D.I., Bostock H. A Distributed-parameter model of the myelinated human motor nerve fibre: Temporal and spatial distributions of action potentials and ionic currents. Biol. Cybern. 1995;73:275–280. doi: 10.1007/BF00201429. [PubMed] [CrossRef] [Google Scholar]</ref><ref>Chiu S.Y., Ritchie J.M. On the physiological role of internodal potassium channels and the security of conduction in myelinated nerve fibres. Proc. R. Soc. Lond. B Biol. Sci. 1984;220:415–422. doi: 10.1098/rspb.1984.0010.[PubMed] [CrossRef] [Google Scholar]</ref><ref>Brismar T., Schwarz J.R. Potassium permeability in rat myelinated nerve fibres. Acta Physiol. Scand. 1985;124:141–148. doi: 10.1111/j.1748-1716.1985.tb07645.x. [PubMed] [CrossRef] [Google Scholar]</ref><ref>Chiu S.Y., Schwarz W. Sodium and potassium currents in acutely demyelinated internodes of rabbit sciatic nerves. J. Physiol. 1987;391:631–649. doi: 10.1113/jphysiol.1987.sp016760. [PMC free article] [PubMed] [CrossRef] [Google Scholar]</ref><ref>Baker M., Bostock H., Grafe P., Martius P. Function and distribution of three types of rectifying channel in rat spinal root myelinated axons. J. Physiol. 1987;383:45–67. [PMC free article] [PubMed] [Google Scholar</ref><ref>Röper J., Schwarz J.R. Heterogeneous distribution of fast and slow potassium channels in myelinated rat nerve fibres. J. Physiol. 1989;416:93–110. doi: 10.1113/jphysiol.1989.sp017751. [PMC free article] [PubMed] [CrossRef] [Google Scholar]</ref><ref>Bittner S., Meuth S.G. Targeting ion channels for the treatment of autoimmune neuroinflammation. Ther. Adv. Neurol. Disord. 2013;6:322–336. doi: 10.1177/1756285613487782. [PMC free article] [PubMed] [CrossRef] [Google Scholar]</ref> Oltre ai canali ionici, le pompe dipendenti dall'energia e altri meccanismi di trasporto ionico forniscono importanti bersagli terapeutici per una serie di disturbi neurologici. <ref>Waxman S.G., Ritchie J.M. Molecular dissection of the myelinated axon. Ann. Neurol. 1993;33:121–136. doi: 10.1002/ana.410330202. [PubMed] [CrossRef] [Google Scholar]</ref><ref>Bittner S., Budde T., Wiendl H., Meuth S.G. From the background to the spotlight: TASK channels in pathological conditions. Brain Pathol. 2010;20:999–1009. doi: 10.1111/j.1750-3639.2010.00407.x. [PMC free article][PubMed] [CrossRef] [Google Scholar]</ref><ref>Ehling P., Bittner S., Budde T., Wiendl H., Meuth S.G. Ion channels in autoimmune neurodegeneration. FEBS Lett. 2011;585:3836–3842. doi: 10.1016/j.febslet.2011.03.065. [PubMed] [CrossRef] [Google Scholar]</ref>A questo proposito, la regolazione dei gradienti ionici transmembrana costa molta energia e diventa essa stessa una considerazione importante (vedi sotto)..<ref name=":19">Hübel N., Dahlem M.A. Dynamics from seconds to hours in Hodgkin-Huxley model with time-dependent ion concentrations and buffer reservoirs. PLoS Comput. Biol. 2014;10:e1003941. doi: 10.1371/journal.pcbi.1003941.[PMC free article] [PubMed] [CrossRef] [Google Scholar]</ref>Ciò è particolarmente vero poiché il piccolo volume degli assoni li rende soggetti a cambiamenti di concentrazione di ioni che possono avere un impatto drammatico sulle forze motrici e possono diventare problematici nei modelli che assumono concentrazioni intracellulari ed extracellulari costanti. Ma anche i modelli recenti hanno affrontato tali problemi (vedi sotto). | |||
Tutti i modelli summenzionati si concentrano sulla simulazione del cambiamento nel potenziale della membrana dell'assone, ma non si ha necessariamente accesso sperimentale a quella variabile, il che ovviamente complica gli sforzi per confrontare la simulazione e i dati sperimentali. Infatti, poiché le registrazioni extracellulari sono la fonte primaria di dati elettrofisiologici da soggetti umani, la descrizione matematica del potenziale del campo extracellulare è di grande interesse clinico. Per il calcolo di questi potenziali vengono utilizzate valutazioni matematiche basate sulle equazioni di Laplace e sulle trasformate di Fourier (a volte indicate come modellazione line-source, ad es. <ref name=":18" /><ref>Ganapathy L., Clark J.W. Extracellular currents and potentials of the active myelinated nerve fibre. Biophys. J. 1987;52:749–761. doi: 10.1016/S0006-3495(87)83269-1. [PMC free article] [PubMed] [CrossRef] [Google Scholar]</ref> | |||
==== | ==== Modellazione di meccanismi specifici ==== | ||
Oltre a modellare la normale funzione assonale, i modelli possono essere utilizzati per esplorare particolari meccanismi di disfunzione assonale, specialmente se combinati con risultati sperimentali che potrebbero individuare meglio i meccanismi.<ref>Prescott S.A. Pathological changes in peripheral nerve excitability. In: Jaeger D., Jung R., editors. Encyclopedia of Computational Neurosci. 1st ed. Springer-Verlag; New York, NY, USA: 2015. [Google Scholar]</ref> Ad esempio, Barrett e Barrett<ref>Barrett E.F., Barrett J.N. Intracellular recording from vertebrate myelinated axons: Mechanism of the depolarizing afterpotential. J. Physiol. 1982;323:117–144. doi: 10.1113/jphysiol.1982.sp014064. [PMC free article] [PubMed] [CrossRef] [Google Scholar]</ref> hanno dimostrato che il potenziale post-potenziale depolarizzante (DAP) è sensibile ai cambiamenti nelle densità di conduttanza e ai cambiamenti capacitivi che potrebbero verificarsi durante la demielinizzazione. Un modello di Blight è stato progettato per la simulazione delle sue condizioni di registrazione sperimentale <ref name=":14" /><ref>Blight A.R., Someya S. Depolarizing afterpotentials in myelinated axons of mammalian spinal cord. Neuroscience. 1985;15:1–12. doi: 10.1016/0306-4522(85)90118-6. [PubMed] [CrossRef] [Google Scholar]</ref> e rappresenta un singolo internodo con più segmenti discreti e nodi e internodi adiacenti in singoli segmenti a parametri concentrati. Questo modello includeva i canali K+ nell'axolemma del singolo internodo multisegmentato e trattava il resto come puramente passivo. | |||
Sulla base di questo lavoro, con particolare attenzione ai dettagli anatomici ed elettrofisiologici, McIntyre et al.<ref name=":17" /> ha affrontato il ruolo del DAP e della post-iperpolarizzazione (AHP) nel ciclo di recupero, il modello distinto di fluttuazione della soglia che segue un singolo potenziale d'azione esibito dai nervi umani. Le simulazioni hanno suggerito ruoli distinti per i canali Na+ e K+ attivi e passivi in entrambi i postpotenziali e hanno proposto che le differenze nella forma AP, nella relazione forza-durata e nel ciclo di recupero delle fibre nervose motorie e sensoriali possano essere attribuite a differenze cinetiche nelle conduttanze nodali del Na+ . Richardson et al.<ref>Richardson A.G., McIntyre C.C., Grill W.M. Modelling the effects of electric fields on nerve fibres: Influence of the myelin sheath. Med. Biol. Eng. Comput. 2000;38:438–446. doi: 10.1007/BF02345014. [PubMed] [CrossRef] [Google Scholar]</ref> ha anche scoperto che è necessaria un'alterazione del modello standard di "isolante perfetto" per riprodurre i DAP durante la stimolazione ad alta frequenza. | |||
Anche la sensibilità alla temperatura degli effetti di demielinizzazione è stata studiata computazionalmente. Zlochiver<ref>Zlochiver S. Persistent reflection underlies ectopic activity in multiple sclerosis: A numerical study. Biol. Cybern. 2010;102:181–196. doi: 10.1007/s00422-009-0361-2. [PubMed] [CrossRef] [Google Scholar]</ref> ha modellato il riflesso risonante persistente attraverso una singola placca di demielinizzazione focale e ha scoperto che questo effetto era sensibile alla temperatura e al diametro dell'assone. Tutti questi esempi hanno dimostrato il potere delle simulazioni di esaminare meccanismi specifici per spiegare i fenomeni osservati dalla clinica e offrire una guida per la ricerca futura. | |||
Come accennato in precedenza, è probabile che cambiamenti distinti nella funzione degli assoni manifestino determinati sintomi di guadagno o perdita di funzione. Se si potessero riprodurre quei cambiamenti in un modello computazionale, le necessarie modifiche ai parametri necessarie per convertire il modello tra funzionamento normale e anormale potrebbero essere utilizzate per prevedere la patologia sottostante. Idealmente questo può portare a esperimenti specifici in cui il canale ionico sospetto, ad esempio, viene manipolato direttamente per vedere se la sua alterazione acuta è sufficiente per riprodurre o invertire alcuni cambiamenti patologici. Recenti studi del laboratorio Prescott illustrano questo processo. <ref>Ratté S., Zhu Y., Lee K.Y., Prescott S.A. Criticality and degeneracy in injury-induced changes in primary afferent excitability and the implications for neuropathic pain. Elife. 2014;3:e02370. doi: 10.7554/eLife.02370.[PMC free article] [PubMed] [CrossRef] [Google Scholar]</ref><ref>Zhu Y., Feng B., Schwartz E.S., Gebhart G.F., Prescott S.A. Novel method to assess axonal excitability using channelrhodopsin-based photoactivation. J. Neurophysiol. 2015;113:2242–2249. doi: 10.1152/jn.00982.2014.[PMC free article] [PubMed] [CrossRef] [Google Scholar]</ref> Il successo di questi studi dipendeva da tecniche avanzate tra cui la tecnica del morsetto dinamico, utilizzata per passare da schemi di spiking normali a quelli anormali e strumenti optogenetici. Il prossimo passo è collegare i cambiamenti nella funzione degli assoni con i sintomi della malattia (oi loro correlati comportamentali nei modelli animali). | |||
Negli esperimenti sui nervi uditivi, Tagoe e colleghi<ref>Tagoe T., Barker M., Jones A., Allcock N., Hamann M. Auditory nerve perinodal dysmyelination in noise-induced hearing loss. J. Neurosci. 2014;12:2684–2688. doi: 10.1523/JNEUROSCI.3977-13.2014.</ref> hanno dimostrato che la perdita dell'udito correlata a cambiamenti morfologici a livello di paranodi e iuxtaparanodi, incluso l'allungamento del nervo uditivo attorno ai nodi di Ranvier, può derivare dall'esposizione a rumori forti. Estendendo questo lavoro, Hamann e colleghi hanno costruito un modello computazionale per esaminare i possibili meccanismi. Il loro modello ha suggerito che è più probabile che una diminuzione della densità dei canali Na, piuttosto che una ridistribuzione dei canali Na o K in generale, sia responsabile dell'inibizione della conduzione associata alla sovraesposizione acustica.<ref>Brown A.M., Hamann M. Computational modeling of the effects of auditory nerve dysmyelination. Front. Neuroanat. 2014;8doi: 10.3389/fnana.2014.00073. [PMC free article] [PubMed] [CrossRef] [Google Scholar]</ref> Questo tandem esperimento-modello dimostra il potenziale rivelatore dell'associazione di modelli computazionali con esperimenti di laboratorio. | |||
Con un modello multistrato di assone mielinizzato, Stephanova e colleghi hanno avuto un successo continuo nell'identificare le probabili carenze anatomiche e fisiologiche alla base di vari sintomi e condizioni correlate alla demielinizzazione, confrontando le misurazioni di tracciamento della soglia dei pazienti, tra cui latenze, refrattarietà (l'aumento della soglia corrente durante il relativo periodo refrattario), periodo refrattario, supernormalità e valori soglia di elettrotono, comprese le misure stimolo-risposta come le relazioni corrente-soglia.<ref name=":5" /> Ad esempio, hanno scoperto che la lieve demielinizzazione sistematica internodale (ISD) è un indicatore specifico della CMT1A. La lieve demielinizzazione sistematica paranodale (PSD) e la demielinizzazione sistematica paranodale (PISD) sono indicatori specifici della CIPD e dei suoi sottotipi. Le gravi demielinizzazioni focali, internodale e paranodale, paranodale-internodale (IFD e PFD, PIFD) sono indicatori specifici di neuropatie demielinizzanti acquisite come GBS e MMN [18] (vedi Figura 1). | |||
La demielinizzazione focale sistematica lieve e grave corrisponde alle neuropatie ereditarie (CMT1A) e acquisite (CIDP, GBS e MMN) (Tabella 1). È stato inoltre riscontrato che il 70% di demielinizzazione sistematica è insufficiente a causare sintomi e il 96% è necessario per il blocco di conduzione a un singolo nodo [18]. Quindi, c'è un grande fattore di sicurezza per la demielinizzazione focale. Con la loro versione dipendente dalla temperatura del modello della fibra nervosa motoria umana mielinizzata, Stephanova e Daskalova<ref>Stephanova D.I., Daskalova M. Electrotonic potentials in simulated chronic inflammatory demyelinating polyneuropathy at 20 °C–42 °C. J. Integr. Neurosci. 2015;27:1–18. doi: 10.1142/S0219635215500119. [PubMed] [CrossRef] [Google Scholar]</ref> hanno dimostrato che i potenziali elettrotonici nei pazienti con CIDP sono ad alto rischio di blocco durante l'ipotermia e anche lieve ipertermia e suggeriscono meccanismi che implicano una maggiore entità della polarizzazione i potenziali elettrotonici internodali nodali e depolarizzanti, il raddrizzatore interno K+ e le correnti di dispersione K+ aumentano con la temperatura e l'adattamento all'iperpolarizzazione di lunga durata è maggiore rispetto alla depolarizzazione.<center> | |||
<center> | |||
{| class="wikitable" | {| class="wikitable" | ||
|+ | |+ | ||
! colspan="2" | | ! colspan="2" |Tabella 1 | ||
Corrispondenza tra tipi di demielinizzazione e malattie secondo Stephanova e Dimitrov.<ref name=":3" /> | |||
|- | |- | ||
! colspan="1" rowspan="1" | | ! colspan="1" rowspan="1" |Tipo di demielinizzazione | ||
! colspan="1" rowspan="1" | | ! colspan="1" rowspan="1" |Malattia corrispondente (PNS) | ||
|- | |- | ||
| colspan="1" rowspan="1" | | | colspan="1" rowspan="1" |Demielinizzazione sistematica internodale (ISD) | ||
| colspan="1" rowspan="1" |Charcot-Marie-Tooth | | colspan="1" rowspan="1" |Malattia di Charcot-Marie-Tooth di tipo 1A (CMT1A) | ||
|- | |- | ||
| colspan="1" rowspan="1" | | | colspan="1" rowspan="1" |Demielinizzazione sistematica paranodale (PSD) | ||
| colspan="1" rowspan="1" | | | colspan="1" rowspan="1" |Polineuropatia demielinizzante infiammatoria cronica (CIDP) | ||
|- | |- | ||
| colspan="1" rowspan="1" | | | colspan="1" rowspan="1" |Sottotipi di demielinizzazione paranodale + internodale (PISD) | ||
| colspan="1" rowspan="1" | | | colspan="1" rowspan="1" |Polineuropatia demielinizzante infiammatoria cronica (CIPD) | ||
|- | |- | ||
| colspan="1" rowspan="1" | | | colspan="1" rowspan="1" |Demielinizzazione focale internodale (IFD) | ||
| colspan="1" rowspan="1" |Guillain-Barré (GBS) | | colspan="1" rowspan="1" |Guillain-Barré (GBS) | ||
|- | |- | ||
| colspan="1" rowspan="1" | | | colspan="1" rowspan="1" |Paranodale + demielinizzazione focale (PIFD) | ||
| colspan="1" rowspan="1" | | | colspan="1" rowspan="1" |Neuropatia motoria multifocale (MMN) | ||
|- | |- | ||
| colspan="1" rowspan="1" |Paranodal + focal demyelination (PIFD) | | colspan="1" rowspan="1" |Paranodal + focal demyelination (PIFD) | ||
| colspan="1" rowspan="1" | | | colspan="1" rowspan="1" |Neuropatia motoria multifocale (MMN) | ||
|} | |} | ||
</center> | </center> | ||
Revision as of 16:24, 16 April 2023
| Title | Dinamiche fisiologiche nelle malattie demielinizzanti: svelare relazioni complesse attraverso la modellazione al computer |
| Authors | Jay S. Coggan · Stefan Bittner · Klaus M. Stiefel · Sven G. Meuth · Steven A. Prescott |
| Source | Document |
| Date | 2021 |
| Journal | Int J Mol Sci. |
| DOI | 10.3390/ijms160921215 |
| PUBMED | https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4613250/#!po=53.5714 |
| PDF copy | |
| License | CC BY |
| This resource has been identified as a Free Scientific Resource, this is why Masticationpedia presents it here as a mean of gratitude toward the Authors, with appreciation for their choice of releasing it open to anyone's access | |
This is free scientific content. It has been released with a free license, this is why we can present it here now, for your convenience. Free knowledge, free access to scientific knowledge is a right of yours; it helps Science to grow, it helps you to have access to Science
This content was relased with a 'CC BY' license.
You might perhaps wish to thank the Author/s
Free resource by Jay S. Coggan · Stefan Bittner · Klaus M. Stiefel · Sven G. Meuth · Steven A. Prescott
|
Abstract
Nonostante le intense ricerche, sono disponibili pochi trattamenti per la maggior parte dei disturbi neurologici. Le malattie demielinizzanti non fanno eccezione. Ciò forse non sorprende considerando la natura multifattoriale di queste malattie, che comportano complesse interazioni tra cellule del sistema immunitario, glia e neuroni. Nel caso della sclerosi multipla, ad esempio, non c'è unanimità tra i ricercatori sulla causa o persino su quale sistema o tipo di cellula potrebbe essere ground zero. Questa situazione preclude lo sviluppo e l'applicazione strategica di terapie basate sui meccanismi. Discuteremo di come la modellazione computazionale applicata a questioni a diversi livelli biologici possa aiutare a collegare insieme osservazioni disparate e decifrare meccanismi complessi le cui soluzioni non sono riconducibili al semplice riduzionismo. Effettuando previsioni verificabili e rivelando lacune critiche nelle conoscenze esistenti, tali modelli possono aiutare a indirizzare la ricerca e forniranno un quadro rigoroso in cui integrare i nuovi dati man mano che vengono raccolti. Al giorno d'oggi, i dati non mancano; la sfida è dare un senso a tutto ciò. A tale riguardo, la modellazione computazionale è uno strumento inestimabile che potrebbe, in ultima analisi, trasformare il modo in cui comprendiamo, diagnostichiamo e trattiamo le malattie demielinizzanti.
Parole chiave: mielina, demielinizzazione, sclerosi multipla, malattia neurodegenerativa, modello computazionale, scoperta di farmaci
Introduzione
I sistemi nervosi dei vertebrati sono spesso divisi in materia grigia e bianca in base al loro aspetto e ai ruoli funzionali corrispondenti. Mentre la materia grigia è costituita in gran parte da corpi cellulari e dendriti, la materia bianca contiene principalmente assoni e prende il nome dai fogli di membrana lipidica chiamati mielina che sono avvolti strettamente attorno a quegli assoni.[1] La mielina proviene da diverse classi di cellule gliali denominate oligodendrociti nel sistema nervoso centrale (SNC) e cellule di Schwann nel sistema nervoso periferico (SNP).
L'isolamento elettrico fornito dai fogli di mielina migliora la funzione assonale aumentando sia l'efficienza energetica che la velocità di conduzione dei potenziali d'azione (AP). Queste due funzioni potrebbero aver cambiato la loro importanza relativa durante l'evoluzione.[2] La mielina è apparsa per la prima volta nell'Ordoviciano (da 485 a 443 ma, o milioni di anni prima del presente) dopo la divisione degli antenati della lampreda e della missina dal resto di linee dei vertebrati.[3] Con alcune interessanti eccezioni, [4][5] la mielina o strutture analoghe si trovano in tutti i vertebrati ed è fondamentale per il corretto funzionamento del loro sistema nervoso. Il tempo approssimativo dell'evoluzione della mielina può essere dedotto dal tempo noto di divergenza tra cordati senza (agnatha) e con (tutti gli altri vertebrati) mielina.
L'avvolgimento della mielina è interrotto da tratti regolarmente distanziati e non mielinizzati noti come nodi di Ranvier. La mielina accelera la conduzione limitando il flusso di carica transmembrana attraverso i canali ionici situati all'interno dei nodi. All'interno dei cosiddetti internodi, la corrente scorre lungo l'assone con una piccola parte che passa attraverso la membrana cellulare isolata. L'AP viene rigenerato in ciascun nodo in cui la densità dei canali del sodio e del potassio voltaggio-dipendenti è molto elevata. Questo processo è chiamato "conduzione saltatoria" poiché l'AP sembra saltare da un nodo all'altro. Le interruzioni in questo sistema di comunicazioni a fuoco rapido possono essere associate a una serie di disfunzioni del sistema nervoso.[6]
Sotto diversi aspetti, gli assoni sembrano operare ai limiti fisici. Un esempio interessante è che la dimensione degli assoni sembra essere limitata dal rumore termico intrinseco alle proteine del canale ionico; qualsiasi assone più sottile di 0,1 μm sarebbe inutile per il trasferimento di informazioni a causa dei suoi elevati livelli di rumore.[7] Curiosamente, 0,1 μm è anche approssimativamente il diametro dell'assone più piccolo osservato nei sistemi nervosi [7]. Questo e risultati simili suggeriscono che gli assoni e le loro sottostrutture sono dispositivi biologici finemente sintonizzati, ma che la sintonizzazione può evidentemente essere interrotta in condizioni patologiche.[8]
La demielinizzazione mette in moto cambiamenti funzionali che sono importanti per le caratteristiche cliniche ma che non sono facilmente spiegabili da cambiamenti immunologici o radiologici. La posizione di una placca prevede quale sistema sarà interessato (motorio vs. sensoriale, visivo vs. tattile) ma non come sarà influenzato. Ciò evidenzia l'importanza di valutare la funzione (oltre alla struttura) e come cambia dopo la demielinizzazione. Dopo aver introdotto le malattie demielinizzanti, discuteremo di come le manifestazioni cliniche di tali malattie riflettano diversi cambiamenti patologici nella funzione degli assoni. Sosterremo che la comprensione di questi cambiamenti e la piena capitalizzazione di tale comprensione per scopi diagnostici e terapeutici possono trarre enormi benefici dalla modellazione computazionale.
Malattie demielinizzanti
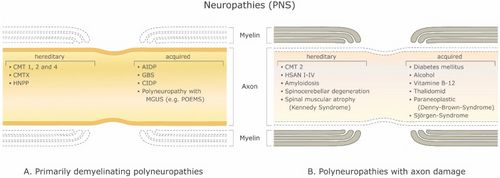
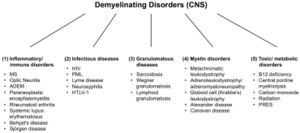
Esiste un gran numero di malattie demielinizzanti che interessano sia il SNP (Figura 1) che il SNC (Figura 2). Le eziologie sono eterogenee e vanno dai disordini genetici ai meccanismi metabolici, infettivi o autoimmuni. La sclerosi multipla (SM) è il più diffuso di questi disturbi, con circa 3 milioni di pazienti in tutto il mondo. La sua causa sottostante è incerta, ma si ritiene che implichi la predisposizione genetica agli agenti ambientali [9][10] e possa coinvolgere componenti immunologiche, di risposta al trauma, biofisiche, genetiche e/o metaboliche.[10] I sintomi e le lesioni devono essere molteplici sia nel tempo che nello spazio. Cioè, ci devono essere più episodi nel tempo, che coinvolgono parti disconnesse del sistema nervoso centrale. Non è chiaro se la demielinizzazione infiammatoria sia un evento primario o secondario all'interno del processo patologico..[9][11][12] La maggior parte dei trattamenti mira al sistema immunitario o alla barriera emato-encefalica, ma anche la gestione dei sintomi neurologici attraverso la modulazione dell'eccitabilità assonale svolge un ruolo importante (vedi sotto).
Valutazione clinica della sclerosi multipla
I sintomi sono diversi e possono verificarsi in tutte le combinazioni all'interno di un singolo paziente. La diagnosi richiede che nel tempo vi siano lesioni multiple ed episodi sintomatici, che coinvolgano parti disconnesse del sistema nervoso centrale. Inoltre, i sintomi tendono ad essere scarsamente correlati con le misure radiologiche. Nella grande maggioranza dei casi, le caratteristiche cliniche individuali non si correlano bene con i risultati della RM, specialmente per le lesioni cerebrali.[13][14][15] Questa dissociazione clinico-radiologica richiede una migliore comprensione teorica dei sintomi della demielinizzazione e dei cambiamenti biofisici sottostanti che li accompagnano, il che ovviamente solleva la questione di cosa accada esattamente agli assoni colpiti.
I sintomi sono spesso intermittenti e possono includere sia la perdita della funzione (sintomi negativi come intorpidimento, debolezza muscolare, formicolio, cecità, incontinenza, perdita della funzione sessuale, perdita di equilibrio, linguaggio confuso, costipazione, affaticamento invalidante, depressione, disfunzione cognitiva , incapacità di deglutire, interruzione dell'andatura e perdita del controllo della respirazione) e guadagno di funzionalità (sintomi positivi come spasmi, spasticità, crampi, dolore, visione offuscata o doppia, urgenza o esitazione urinaria, nausea, tra gli altri).[16] I primi criteri diagnostici differenziali includono il segno di Lhermitte (sensazioni legate alla flessione del collo) e il fenomeno di Uhthoff (peggioramento dei sintomi dipendente dalla temperatura). La diagnosi differenziale di SM segue strettamente i criteri di McDonald.[17]
Negli studi diagnostici umani sui potenziali evocati visivi, sensoriali o motori (VEP, SEP, MEP), solo la latenza o la velocità di conduzione possono essere misurate con precisione (con variazioni di circa il 30-40% tra i diversi laboratori). Ma queste misure danno pochi indizi sui meccanismi sottostanti che coinvolgono il rallentamento o il blocco della conduzione, o fattori morfologici o funzionali come ramificazione, demielinizzazione, rimielinizzazione, assottigliamento assonale (diminuzione dell'area della sezione trasversale), attenuazione o ricrescita, cambiamenti di conduzione legati alla temperatura , o malpolarizzazione (iper o ipo). Tuttavia, il tipo di lesione demielinizzante può fornire indizi sull'eziologia e quindi guidare il trattamento; ad esempio, i fattori genetici sembrano essere maggiormente correlati ai processi patologici internodali e le disfunzioni immunologiche causano anomalie paranodali.[18]
Un certo numero di test viene abitualmente utilizzato per valutare la funzione neurale. Nell'elettroneurografia, un breve stimolo elettrico viene applicato a un nervo periferico in una posizione anatomicamente predefinita per misurare la latenza e l'ampiezza del potenziale d'azione composto in un'altra posizione lungo il nervo. I risultati devono essere interpretati in combinazione con risultati clinici e test (ad esempio, elettromiografia) ma, soprattutto, diverse malattie mostrano diversi modelli di cambiamenti elettroneurografici. Questo è importante non solo per scopi diagnostici, ma può anche indicare specifici cambiamenti patologici nella funzione degli assoni che potrebbero, a loro volta, aiutare a guidare la scelta della terapia (se la patobiologia degli assoni fosse compresa; vedi sotto). Utilizzando il monitoraggio della soglia, l'eccitabilità è stata misurata negli esseri umani per diverse malattie demielinizzanti periferiche tra cui la malattia di Charcot-Marie-Tooth di tipo 1A (CMT1A), la polineuropatia demielinizzante infiammatoria cronica (CIDP), la sindrome di Guillain-Barré (GBS) e la neuropatia motoria multifocale (MMN )..[19][20][21][22][23][24][25] La sfida sta nell'interpretare queste osservazioni. A tal fine, il gruppo di Stephanova ha simulato gradi progressivamente maggiori di demielinizzazione sistematica e focale delle fibre motorie per cercare di spiegare i cambiamenti fisiologici osservati [26][27][28][29][30][31] (vedere la sezione Modellazione di seguito).
Coinvolgimento dei corpi cellulari
La progressione dalla SM recidivante-remittente (RRMS) alla SM secondaria progressiva (SPMS) è associata a un maggiore coinvolgimento della patologia della materia grigia, sebbene il coinvolgimento assonale/della materia grigia possa essere osservato già nelle prime fasi della malattia. [32][33][34][35] Il danno alla materia grigia è considerato il meccanismo alla base della progressione della malattia e della disabilità permanente nei pazienti con SM ed è misurato dalla perdita della frazione parenchimale cerebrale o del volume cerebrale mediante risonanza magnetica o clinicamente dalla progressione sulla scala dello stato di disabilità ampliata (EDSS).[36] La transizione dalla SMRR alla SMSP è un presagio per la mancanza di terapie per combattere l'esacerbato deterioramento fisico e cognitivo che la maggior parte dei pazienti con SMSM deve affrontare. [9][37]
Trattamento
I principali interventi per la SM riguardano la modulazione della risposta immunitaria con, ad esempio, metil-prednisolone, interferone beta, glatiramer acetato o fingolimod, o impedendo alle cellule infiammatorie di attraversare la BBB (anticorpi monoclonali, ad es. Tysabri (anti α4-integrina, Natalizumab )). Molto recentemente i primi due agenti orali (fumarato e teriflunomide) e l'anticorpo anti-CD52 Natalizumab sono stati approvati per il trattamento della SMRR, che può essere trattata con successo con terapie di prima linea come interferoni, glatiramer acetato o fingolimod, o con terapie di seconda linea, ma le forme progressive (PPMS, SPMS) rappresentano ancora un bisogno biomedico insoddisfatto.[38] Gli antineoplastici sono utilizzati in casi estremamente avanzati o difficili.[39]
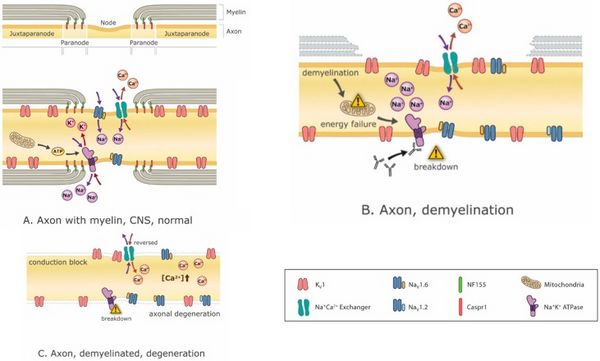
I farmaci modificanti la malattia sono fondamentali per arrestare o almeno attenuare il processo di demielinizzazione, ma lo è anche per gestire i sintomi derivanti da qualunque demielinizzazione sia già avvenuta. La modulazione del canale ionico è sempre più promettente con l'avvento di nuovi bloccanti del canale ionico come Ampyra (blocco del canale K). [40][41] Il blocco del canale del potassio ha lo scopo di migliorare l'eccitabilità degli assoni. Il problema è che tali interventi, sebbene efficaci nel trattamento dei sintomi negativi e nel ripristino della funzione, tendono ad esacerbare i sintomi positivi.[42] Al contrario, il trattamento di sintomi positivi come gli spasmi con antiepilettici come la carbamazepina, ad esempio, può esacerbare i sintomi negativi.[43] Infatti, il blocco dei canali del Na+ non solo riduce i sintomi positivi, ma può anche essere neuroprotettivo (poiché l'accumulo di Na+ fa sì che i meccanismi di scambio Na+/Ca2+ carichino i neuroni con Ca2+, che è eccitotossico)[44] (Figura 3) ma questi benefici vanno a scapito dei sintomi. Pertanto, e specialmente in un paziente che presenta una combinazione di sintomi positivi e negativi, le opzioni di trattamento sono limitate.
La discussione di cui sopra solleva il punto importante che, sebbene sia stato fatto molto rumore sui meccanismi immunitari, la loro connessione con i cambiamenti clinici è in gran parte correlazionale. Bisogna considerare gli effetti intermedi sulla funzione assonale, vale a dire i cambiamenti primari e secondari (compensativi) nell'eccitabilità degli assoni, per apprezzare come la funzione neurologica è alterata. Questi cambiamenti non sono conseguenze semplici e dirette della demielinizzazione ma, invece, suggeriscono che la stessa fisiologia assonale cambia in risposta alla demielinizzazione. Alcuni di questi cambiamenti sono adattivi mentre altri sono disadattivi, o forse i cambiamenti adattivi possono diventare disadattivi man mano che la situazione (stato di mielinizzazione) si evolve. Se i cambiamenti nella fisiologia assonale determinano la manifestazione di vari sintomi, la gestione dei sintomi ricadrà in gran parte su trattamenti che mirano a manipolare la fisiologia degli assoni. Lo sviluppo strategico di tali trattamenti richiede una profonda comprensione meccanicistica dell'eccitabilità assonale e della sua regolazione.
Patobiologia degli assoni
Cambiamenti strutturali e molecolari
Gli assoni sono profondamente influenzati dalla demielinizzazione. La morfologia dell'assone diventa irregolare o rigonfia, spesso con un aspetto a perline. Si osserva anche un accumulo focale di proteine (tramite trasporto assonale veloce). Nelle placche attive croniche, la perdita assonale del 20%-80% è evidente all'interno della sostanza bianca peri-placca e della normale sostanza bianca distante.[45] Nelle placche attive precoci e croniche, si ritiene che il danno sia causato da fattori infiammatori e immunitari rilasciati durante la demielinizzazione infiammatoria acuta. I mediatori proposti includono proteasi, citochine, eccitotossine e radicali liberi. Gli antigeni neuronali sono bersagli della reazione immunitaria che porta all'infiammazione del sistema nervoso centrale. Altri fattori che causano la disfunzione assonale o la morte includono una mancanza di supporto trofico da mielina e oligodendrociti, danni da fattori immunitari solubili o cellulari ancora presenti nella placca inattiva e insufficienza mitocondriale cronica nell'ambito di una maggiore richiesta di energia.[46] Un ruolo critico per gli oligodendrociti e le cellule di Schwann nella sopravvivenza degli assoni è stato anche attribuito ai perossisomi, al metabolismo lipidico e alla disintossicazione delle specie reattive dell'ossigeno (ROS).[47]
La rimielinizzazione è spesso osservata come placche ombra formate dal reclutamento di precursori di oligodendrociti indifferenziati che migrano e circondano le lesioni consentendo sottili strati di rimielinizzazione.[48] Questo processo si verifica principalmente nelle placche attive acute, ma anche nelle fasi croniche. Questa osservazione ha innescato lo sviluppo di un nuovo anticorpo monoclonale diretto contro LINGO-1 (Anti-LINGO-1). Il legame di LINGO-1 ai recettori Nogo previene i processi di rimielinizzazione nel SNC; l'inibizione di questa interazione consente quindi una significativa rimielinizzazione negli animali con encefalomielite autoimmune sperimentale.[49]
Durante il processo patologico, i linfociti autoreattivi e i macrofagi possono attraversare la barriera ematoencefalica e accumularsi nel cervello e nel midollo spinale.[50] I linfociti regolatori (Tregs) non riescono a sopprimere le cellule effettrici, per lo più cellule CD8+ citotossiche.[51] Il rilascio di citochine pro-infiammatorie recluta la microglia ingenua, che entra in contatto con un'unità oligodendrocita-mielina mediante interazioni con Fc e recettori del complemento. Un segnale citotossico che innesca la morte viene quindi trasmesso attraverso il fattore di necrosi tumorale α (TNFα)[52] legato alla superficie. Ciò si verifica in concerto con un esteso danno assonale.[10]
Lucchinetti el al.[46] proposto quattro distinti immunopattern di formazione della placca riscontrati in pazienti in diversi stadi della malattia. Le placche di tipo I e II sono dominate dall'infiammazione dei linfociti T e dei macrofagi e si pensa che mimino rispettivamente i modelli di encefalomielite autoimmune a cellula T o a cellula T più anticorpi. La perdita di mielina nelle placche di tipo I può essere causata da fattori tossici rilasciati dai macrofagi attivati, mentre la deposizione di IgG e complemento suggerisce un ruolo degli anticorpi nelle placche di tipo II. Al contrario, i modelli III e IV mostrano una grande distrofia degli oligodendrociti. Si ritiene che il pattern III sia correlato alle lesioni indotte dall'ipossia che sono guidate da difetti nella funzione mitocondriale,[53] mentre le lesioni del pattern IV sono associate a morte profonda non apoptotica degli oligodendrociti nella sostanza bianca periplacca.
Barnett e Prineas[54] hanno analizzato le lesioni dei pazienti subito dopo l'inizio di una ricaduta, durante la quale era in corso la formazione attiva della placca. I loro risultati suggeriscono che l'apoptosi degli oligodendrociti e l'attivazione gliale si verificano durante la formazione precoce della placca attiva in assenza di linfociti infiammatori o fagociti della mielina. Hanno proposto che la vulnerabilità degli oligodendrociti, descritta nel modello di tipo III di Lucchinetti, sia presente nelle prime fasi di tutta la formazione della placca ed è l'innesco per la successiva necrosi post apoptotica che avvia la fagocitosi della mielina da parte dei macrofagi nelle fasi successive. Le analisi in vitro di questo processo hanno implicato cascate del complemento, fattori di necrosi tumorale o secondi messaggeri gassosi.[55] Sebbene l'identificazione delle placche e il monitoraggio del loro progresso abbiano un importante valore clinico, esiste solo una modesta correlazione tra il carico della lesione demielinizzante determinato dalla risonanza magnetica convenzionale e la disabilità clinica dei pazienti con SM (vedi sopra).
Modifiche funzionali
I meccanismi di compromissione funzionale durante la demielinizzazione spesso includono l'interruzione degli ioni Na+, K+ e Ca2+ transmembrana, la dispersione dei canali ionici corrispondenti, una diminuzione dell'efficienza della conduzione AP e una conseguente crisi metabolica (Figura 3). La demielinizzazione può facilmente spiegare il fallimento della conduzione all'interno dell'assone interessato. Se la conduzione non fallisce completamente, la velocità di conduzione può comunque essere rallentata e il rallentamento differenziale tra diversi assoni può causare ritardi di conduzione variabili che si traducono in picchi desincronizzati.
La demielinizzazione consente inoltre agli assoni denudati di avvicinarsi strettamente, ponendo così le basi per le interazioni epatiche e il crosstalk.[10] La riflessione può anche verificarsi a causa della mancata corrispondenza di impedenza tra le lunghezze mielinizzate e non mielinizzate dell'assone. D'altra parte, l'ipereccitabilità non può essere direttamente attribuita alla demielinizzazione; invece, i cambiamenti secondari nell'eccitabilità intrinseca devono essere invocati per spiegare fenomeni come la generazione di picchi ectopici e la post-dimissione (AD). Le alterazioni dell'eccitabilità rappresentano probabilmente cambiamenti compensatori volti a ripristinare la funzione in seguito all'interruzione causata direttamente dalla demielinizzazione, coerente con un processo denominato plasticità omeostatica,[56] ma tale compensazione può evidentemente essere disadattativa. Ciascuno dei suddetti esiti, che non si escludono a vicenda, contribuisce a produrre diversi sintomi osservati nelle malattie demielinizzanti.
I sintomi parossistici caratterizzati dall'insorgenza improvvisa o dall'intensificazione di sintomi come spasmo o dolore lancinante derivano probabilmente dall'AD o da picchi di tipo burst inappropriati. Tali modelli di spiking suggeriscono interazioni altamente non lineari tra le correnti ioniche che contribuiscono [57][58] e potrebbero, almeno in teoria, coinvolgere interazioni tra diverse regioni del neurone.[59] A differenza di forme più generiche di ipereccitabilità (ad esempio, aumento della frequenza di scarica o soglia ridotta), questi modelli specifici sono limitati in termini di precisi meccanismi attraverso i quali potrebbero insorgere. Pertanto, l'identificazione dei cambiamenti del canale ionico alla base di quelle specifiche forme di ipereccitabilità può aiutare a limitare la ricerca dei cambiamenti del canale ionico responsabili delle forme associate, ma meno distintive, di ipereccitabilità.
L'interruzione dell'equilibrio energetico in un neurone potrebbe anche avere un impatto profondo sul benessere del neurone (Figura 3). In effetti, le modifiche compensative possono riuscire a ripristinare alcune funzioni ma, senza invertire il problema principale, possono sorgere altri problemi. Ad esempio, anche se il blocco di conduzione è impedito da un'appropriata variazione compensativa dell'eccitabilità (cioè, una che non si traduca in ipereccitabilità), il sistema può essere meno efficiente dal punto di vista energetico. La perdita del risparmio energetico offerto dalla conduzione saltatoria induce una produzione compensativa di energia mitocondriale che può provocare danni ossidativi e neurodegenerazione. [53][60][61]
Tenere traccia di questo lungo elenco di cambiamenti neurobiologici, comprendere le interrelazioni tra tali cambiamenti e, in definitiva, collegare tali cambiamenti con manifestazioni cliniche e applicare un trattamento efficace non è un compito facile. A tal fine, la modellazione computazionale è uno strumento prezioso. Le simulazioni non solo servono a organizzare le informazioni già note, ma identificano anche lacune cruciali nella conoscenza. L'uso giudizioso della modellazione computazionale può quindi consentire una comprensione più completa e facilitare l'applicazione più efficace di tale comprensione, come discusso di seguito.
Modellazione computazionale
Soprattutto se abbinata agli esperimenti tradizionali, la modellazione computazionale è indispensabile per dare un senso a dati incoerenti e meccanismi complessi. Questi benefici sono esemplificati dall'applicazione di simulazioni in altri campi, come l'epilessia.[62] Qui esaminiamo parte della storia della modellazione computazionale di assoni, conduttanze ioniche, fisiologia della mielina e demielinizzazione, sistema immunitario, mitocondri e altri fattori biologici che sono fondamentali per comprendere le malattie demielinizzanti. La nostra recensione non è esaustiva, ma fornirà un'ampia introduzione agli sforzi passati, presenti e futuri in questo settore.
Modellazione degli assoni
La modellazione computazionale degli assoni si è evoluta tassonomicamente, dai calamari ai tessuti dei mammiferi con un corrispondente aumento di sofisticazione. Il modello di Hodgkin e Huxley (HH), che ha fornito la prima spiegazione completa della generazione di AP, è stato derivato da esperimenti in assoni giganti non mielinizzati di calamari,,[63][64] ma questo primo modello ha dimostrato di essere uno strumento inestimabile da cui successivamente , si sono evoluti modelli più sofisticati di assoni mielinizzati.
L'eterogeneità spaziale e biofisica conferita dall'aggiunta di mielina, e la conseguente formazione di nodi e regioni internodali, rappresenta un aumento significativo della complessità degli assoni. Il primo modello computazionale di un assone mielinizzato era un modello unidimensionale che faceva collassare la guaina mielinica nell'assolemma passivo sottostante, utilizzava una dimensione del passo spaziale uniforme per formare l'approssimazione discreta utilizzata nella soluzione numerica e impiegava una caratterizzazione HH della membrana nodale.[65] Goldman & Albus[66] hanno modificato questo modello per includere una descrizione della membrana nodale derivata dai dati sperimentali sulle fibre nervose mielinizzate di Xenopus laevis come determinato da Frankenhaeuser & Huxley.[67] Studi successivi hanno utilizzato la stessa forma base per il modello con alcune varianti per la rappresentazione dell'axolemma. [15][68][69][70][71][72][73][74][75][76] Il modello a cavo singolo, che descrive l'assone e tutte le sue proprietà di conduttanza e capacità in un'equazione di cavo, ha dominato il campo fino ai giorni nostri nonostante l'introduzione di modelli a cavo doppio da parte di Blight.[77] Nei modelli a doppio cavo, l'axolemma internodale e la guaina mielinica sono rappresentati indipendentemente. Il modello a doppio cavo è stato ampliato da Halter e Clark[78] per esplorare gli effetti della complessa geometria degli oligodendrociti del SNC (o cellule di Schwann nel caso del SNP).
I modelli più recenti hanno anche migliorato le precedenti semplificazioni, tra cui la complessità anatomica del nodo di Ranvier, la distribuzione dei canali ionici nell'assone sotto la guaina mielinica, le diverse proprietà elettriche della guaina mielinica e dell'axolemma e la sistemazione del possibile flusso di corrente all'interno lo spazio periassonale. [78][79][80][81][82] Le rappresentazioni anatomiche dell'area paranodale hanno consentito una valutazione più dettagliata degli effetti della lesione cerebrale traumatica (TBI) sugli assoni mielinizzati.[83] Uno dei modelli anatomicamente più sofisticati include la rappresentazione della complessa struttura della guaina acquosa delle lamelle mieliniche come una serie di lamelle parallele interconnesse in un modello di nervi motori. [30][80]
I modelli più recenti hanno anche considerato la distribuzione non uniforme dei canali ionici in tutto l'assone [19][84][85][86][87][88][89][90] Oltre ai canali ionici, le pompe dipendenti dall'energia e altri meccanismi di trasporto ionico forniscono importanti bersagli terapeutici per una serie di disturbi neurologici. [91][92][93]A questo proposito, la regolazione dei gradienti ionici transmembrana costa molta energia e diventa essa stessa una considerazione importante (vedi sotto)..[94]Ciò è particolarmente vero poiché il piccolo volume degli assoni li rende soggetti a cambiamenti di concentrazione di ioni che possono avere un impatto drammatico sulle forze motrici e possono diventare problematici nei modelli che assumono concentrazioni intracellulari ed extracellulari costanti. Ma anche i modelli recenti hanno affrontato tali problemi (vedi sotto).
Tutti i modelli summenzionati si concentrano sulla simulazione del cambiamento nel potenziale della membrana dell'assone, ma non si ha necessariamente accesso sperimentale a quella variabile, il che ovviamente complica gli sforzi per confrontare la simulazione e i dati sperimentali. Infatti, poiché le registrazioni extracellulari sono la fonte primaria di dati elettrofisiologici da soggetti umani, la descrizione matematica del potenziale del campo extracellulare è di grande interesse clinico. Per il calcolo di questi potenziali vengono utilizzate valutazioni matematiche basate sulle equazioni di Laplace e sulle trasformate di Fourier (a volte indicate come modellazione line-source, ad es. [82][95]
Modellazione di meccanismi specifici
Oltre a modellare la normale funzione assonale, i modelli possono essere utilizzati per esplorare particolari meccanismi di disfunzione assonale, specialmente se combinati con risultati sperimentali che potrebbero individuare meglio i meccanismi.[96] Ad esempio, Barrett e Barrett[97] hanno dimostrato che il potenziale post-potenziale depolarizzante (DAP) è sensibile ai cambiamenti nelle densità di conduttanza e ai cambiamenti capacitivi che potrebbero verificarsi durante la demielinizzazione. Un modello di Blight è stato progettato per la simulazione delle sue condizioni di registrazione sperimentale [77][98] e rappresenta un singolo internodo con più segmenti discreti e nodi e internodi adiacenti in singoli segmenti a parametri concentrati. Questo modello includeva i canali K+ nell'axolemma del singolo internodo multisegmentato e trattava il resto come puramente passivo.
Sulla base di questo lavoro, con particolare attenzione ai dettagli anatomici ed elettrofisiologici, McIntyre et al.[81] ha affrontato il ruolo del DAP e della post-iperpolarizzazione (AHP) nel ciclo di recupero, il modello distinto di fluttuazione della soglia che segue un singolo potenziale d'azione esibito dai nervi umani. Le simulazioni hanno suggerito ruoli distinti per i canali Na+ e K+ attivi e passivi in entrambi i postpotenziali e hanno proposto che le differenze nella forma AP, nella relazione forza-durata e nel ciclo di recupero delle fibre nervose motorie e sensoriali possano essere attribuite a differenze cinetiche nelle conduttanze nodali del Na+ . Richardson et al.[99] ha anche scoperto che è necessaria un'alterazione del modello standard di "isolante perfetto" per riprodurre i DAP durante la stimolazione ad alta frequenza.
Anche la sensibilità alla temperatura degli effetti di demielinizzazione è stata studiata computazionalmente. Zlochiver[100] ha modellato il riflesso risonante persistente attraverso una singola placca di demielinizzazione focale e ha scoperto che questo effetto era sensibile alla temperatura e al diametro dell'assone. Tutti questi esempi hanno dimostrato il potere delle simulazioni di esaminare meccanismi specifici per spiegare i fenomeni osservati dalla clinica e offrire una guida per la ricerca futura.
Come accennato in precedenza, è probabile che cambiamenti distinti nella funzione degli assoni manifestino determinati sintomi di guadagno o perdita di funzione. Se si potessero riprodurre quei cambiamenti in un modello computazionale, le necessarie modifiche ai parametri necessarie per convertire il modello tra funzionamento normale e anormale potrebbero essere utilizzate per prevedere la patologia sottostante. Idealmente questo può portare a esperimenti specifici in cui il canale ionico sospetto, ad esempio, viene manipolato direttamente per vedere se la sua alterazione acuta è sufficiente per riprodurre o invertire alcuni cambiamenti patologici. Recenti studi del laboratorio Prescott illustrano questo processo. [101][102] Il successo di questi studi dipendeva da tecniche avanzate tra cui la tecnica del morsetto dinamico, utilizzata per passare da schemi di spiking normali a quelli anormali e strumenti optogenetici. Il prossimo passo è collegare i cambiamenti nella funzione degli assoni con i sintomi della malattia (oi loro correlati comportamentali nei modelli animali).
Negli esperimenti sui nervi uditivi, Tagoe e colleghi[103] hanno dimostrato che la perdita dell'udito correlata a cambiamenti morfologici a livello di paranodi e iuxtaparanodi, incluso l'allungamento del nervo uditivo attorno ai nodi di Ranvier, può derivare dall'esposizione a rumori forti. Estendendo questo lavoro, Hamann e colleghi hanno costruito un modello computazionale per esaminare i possibili meccanismi. Il loro modello ha suggerito che è più probabile che una diminuzione della densità dei canali Na, piuttosto che una ridistribuzione dei canali Na o K in generale, sia responsabile dell'inibizione della conduzione associata alla sovraesposizione acustica.[104] Questo tandem esperimento-modello dimostra il potenziale rivelatore dell'associazione di modelli computazionali con esperimenti di laboratorio.
Con un modello multistrato di assone mielinizzato, Stephanova e colleghi hanno avuto un successo continuo nell'identificare le probabili carenze anatomiche e fisiologiche alla base di vari sintomi e condizioni correlate alla demielinizzazione, confrontando le misurazioni di tracciamento della soglia dei pazienti, tra cui latenze, refrattarietà (l'aumento della soglia corrente durante il relativo periodo refrattario), periodo refrattario, supernormalità e valori soglia di elettrotono, comprese le misure stimolo-risposta come le relazioni corrente-soglia.[21] Ad esempio, hanno scoperto che la lieve demielinizzazione sistematica internodale (ISD) è un indicatore specifico della CMT1A. La lieve demielinizzazione sistematica paranodale (PSD) e la demielinizzazione sistematica paranodale (PISD) sono indicatori specifici della CIPD e dei suoi sottotipi. Le gravi demielinizzazioni focali, internodale e paranodale, paranodale-internodale (IFD e PFD, PIFD) sono indicatori specifici di neuropatie demielinizzanti acquisite come GBS e MMN [18] (vedi Figura 1).
La demielinizzazione focale sistematica lieve e grave corrisponde alle neuropatie ereditarie (CMT1A) e acquisite (CIDP, GBS e MMN) (Tabella 1). È stato inoltre riscontrato che il 70% di demielinizzazione sistematica è insufficiente a causare sintomi e il 96% è necessario per il blocco di conduzione a un singolo nodo [18]. Quindi, c'è un grande fattore di sicurezza per la demielinizzazione focale. Con la loro versione dipendente dalla temperatura del modello della fibra nervosa motoria umana mielinizzata, Stephanova e Daskalova[105] hanno dimostrato che i potenziali elettrotonici nei pazienti con CIDP sono ad alto rischio di blocco durante l'ipotermia e anche lieve ipertermia e suggeriscono meccanismi che implicano una maggiore entità della polarizzazione i potenziali elettrotonici internodali nodali e depolarizzanti, il raddrizzatore interno K+ e le correnti di dispersione K+ aumentano con la temperatura e l'adattamento all'iperpolarizzazione di lunga durata è maggiore rispetto alla depolarizzazione.
| Tabella 1
Corrispondenza tra tipi di demielinizzazione e malattie secondo Stephanova e Dimitrov.[18] | |
|---|---|
| Tipo di demielinizzazione | Malattia corrispondente (PNS) |
| Demielinizzazione sistematica internodale (ISD) | Malattia di Charcot-Marie-Tooth di tipo 1A (CMT1A) |
| Demielinizzazione sistematica paranodale (PSD) | Polineuropatia demielinizzante infiammatoria cronica (CIDP) |
| Sottotipi di demielinizzazione paranodale + internodale (PISD) | Polineuropatia demielinizzante infiammatoria cronica (CIPD) |
| Demielinizzazione focale internodale (IFD) | Guillain-Barré (GBS) |
| Paranodale + demielinizzazione focale (PIFD) | Neuropatia motoria multifocale (MMN) |
| Paranodal + focal demyelination (PIFD) | Neuropatia motoria multifocale (MMN) |
Simple Models and Nonlinear Dynamical Analysis
Given the temporal dissociation between the manifestation of symptoms and the rates of demyelination and remyelination, homeostatic processes undoubtedly occur within axons, which include the redistribution of ion channels in demyelinated plaques.[106][107] But given the diversity of ion channels expressed by different axons and only patchy knowledge of how expression levels change, building detailed models to investigate those homeostatic processes is problematic. Especially under those conditions, highly simplified models can help identify fundamental principles, as exemplified by joint use of modified HH and Morris-Lecar models [57,58]. The results of those studies suggested a simple explanation for the breadth of symptoms encountered during demyelination by revealing that the ratio of Na+ to leak K+ conductance, g(Na)/g(L), acted as a four-way switch controlling excitability patterns that included failure of AP propagation, normal AP propagation, AD, and spontaneous spiking.
Further studies with this model suggested the potential for competition or cooperation between different regions of the same neuron.[59] Cooperativity between remote sites of ectopic spiking allows AD to be initiated and maintained at different locations within a single axon, thus providing a compelling explanation for the temporal and spatial discontinuities of pain and other symptoms presented by MS patients. Remarkably, in a recent study of demyelinated axons in a cuprizone mouse model, experimental evidence was seen for a redistribution of ion channels from the node of Ranvier, enhanced ectopic excitability along with antidromically propagated APs from the demyelinated plaque, as well as a compensatory shift in the excitability of membranes proximal to the soma.[108] All of these observations concur or are consistent with the computational model predictions of Coggan and colleagues and imply the success of the computational approach to guiding laboratory studies.
Furthermore, these simplified models enabled application of mathematical tools to examine the nonlinear mechanisms by which AD is initiated and terminated.[57][58][59] Bifurcation analysis revealed the underlying bistability of axon excitability under pathological conditions, as well as the factors controlling the transition from one attractor state to another. AD, for example, requires a slow inward current that allows for two stable attractor states, one corresponding to quiescence and the other to repetitive spiking (a limit cycle). Termination of AD was explained by the attractor associated with repetitive spiking being destroyed. This occurred when ultra-slow negative feedback in the form of intracellular Na+ accumulation caused the destruction of the limit-cycle attractor state [58]. Other studies using bifurcation analysis suggest that ion concentration changes can introduce slow dynamics that may be important for understanding pathological outcomes [94,109].[94][109]
Modeling at Small Scales
Studies mentioned above highlight the importance of ion concentration changes but each of them only considered those changes at a relatively course scale. By comparison, the study by Lorpreore et al.[110] tackled the daunting problem of modeling three-dimensional electro-diffusion of ion fluxes in micro and nano-domains surrounding ion channels at the node of Ranvier. In this unique model, the fluxes of ions are calculated by Poisson-Nernst-Planck equations with finite volume techniques. The fluxes and electric potentials were evaluated within voxels formed by a Delaunay-Voronoi mesh of the axon interior and exterior close to the membrane. Importantly, the algorithm was validated and results agreed with cable model predictions. Divergence from cable model predictions at smaller cluster sizes revealed the importance of each channel’s own electric field.
The above example highlights the point that models can simulate more than ion channels and membrane potential. Indeed, models can and must dig deeper into biophysical mechanisms like electro-diffusion and into signaling pathways that ultimately serve to regulate ion channel function and expression. A promising method called Biochemical Systems Theory (BST) may be useful in the future for pre-screening the effects of drugs at the systemic level. Broome and Coleman[111] demonstrated the power of this technique by modeling several biochemical pathways in neurons associated with cell death during MS including reactive oxygen and nitrogen species formation, Ca2+ dynamics, death complex formation, apoptotic factor release, and inflammatory responses together with three different states: normal, MS disease and treatment. At the atomic-level, a computational model of myelin basic protein (MBP) structure was carried-out because post-translational modifications of MBP may contribute to demyelination in MS.[112] It is important to understand its 3D structure to predict interaction sites with other molecules but a crystal structure for this protein might never be measured directly. This type of modeling may, therefore, represent an effective way to predict the structure by combining knowledge of amino acid sequence with information from similar proteins. The challenge for and the true power of modeling lies in connecting mechanisms that operate at vastly different scales, from molecular structure to the nervous system as a whole, and beyond, to address how the nervous system interacts with the immune system.
Models of Immune Factors. While there are numerous computational models of the immune system,[113] those related to MS typically model genetic interaction networks, either represented as sets of ordinary differential equations (ODEs) or Boolean networks. One systems biology model of a possible cellular mechanism of RRMS found breakdown in homeostasis of effector (Teff) and regulatory T (Treg) cells.[114][115] By changing parameters in the Teff-Treg feedback loop, under continual stochastic external stimulus from antigens, the model reproduced spontaneous and apparently stochastic immune relapses. The irreversible damage from each episode accumulates over time. Novel predictions include the suggestion that the timing of Treg immunotherapy in the immune response cycle is critical in determining whether intervention is beneficial or deleterious.
Models of Mitochondrial Dysfunction. As mentioned above, myelin enables more energy efficient AP conduction along the axon. The increased energy demands placed on the demyelinated axon represents yet another challenge to the afflicted neuron. Beyond the loss of saltatory conduction, there is mounting evidence of a critical role for astrocytes and oligodendrocytes in supplying energy to neurons and this process has also been the subject of computational modeling.[116]
There are many ways mitochondrial function can go awry and the compensatory pathways are equally complicated.[53][60][61] For example, mitochondrial dysfunction can be rooted in perturbed Ca2+ signaling within mitochondria, disrupted proton gradients or electron chain, reduction-oxidation imbalance as well as the consequences of reduced ATP availability, locally and globally. Multi-scale models of heart, for example, have been used to link altered mitochrondrial Ca2+ signaling to arrhythmia [60]. Using mitochondrial network modeling, this study demonstrated how even slightly too much reactive oxygen species can trigger a cell-wide collapse of mitochondrial membrane potential. This is an excellent example of how a computational model can link processes occurring at different levels, and it is precisely these linkages that must be established in the field of demyelination diseases.
Missing Links and the Need for Integration
Within the field of demyelinating diseases, modeling efforts have traditionally focused on axon models aimed at explaining various aspects of excitability. But as outlined above, those models have undergone tremendous evolution in complexity. In the process, models at different biological scales have begun to coalesce. For instance, models have now begun to address the regulation of ion concentrations and the consequences thereof for slow excitability changes, energy consumption, and toxicity. A computational approach will be necessary for integrating parallel and multifactorial etiologies associated with cognitive decline such as immune system signaling, energy metabolism, grey and white matter interactions, and genetic networks [117].[117] These continued efforts are starting to uncover the vast and interconnected feedback loops that operate across a broad range of spatial and temporal scales. That said, such efforts are still in their infancy and wide gaps remain in the modeling of demyelinating diseases. It is easier to describe what has been modeled than what has not. A truly integrated model involving multiple cell types that addresses all the hypothesized etiological factors remains unrealized. Among the unexplored or under-explored but potentially useful targets for modeling are grey matter pathology, myelin sheath aqueous layers, energy metabolism, and perhaps most importantly, multi-scale or integrated modeling. One should recognize that the necessary tools exist in other fields of study and can, therefore, be readily applied to the study of demyelination diseases.
Conclusions
The normal physiological function of the CNS or PNS relies on a highly regulated interplay of neurons, glia, vasculature and immune cells. This process encompasses and integrates numerous cellular and signaling components that produce a dynamical, computational whole. When any part goes awry, the entire system is forced to compensate. Even when compensation manages to rescue the most obvious consequences of demyelination, certain processes may not return to a completely normal state, which can lead to problems on longer time scales. The resulting symptoms are a confusing mixture of direct and compensatory changes that continuously evolve. The overall complexity has proven to be intractable to efficient experimental dissection. The application of computational modeling techniques represents an invaluable approach to help break the impasse and engender a new era of understanding and discovery.
Acknowledgments
Support provided by the Canadian Institutes of Health Research New Investigator Award and the Ontario Early Researcher Award (SAP). We thank Heiki Blum for assistance with figure preparation.
Author Contributions
All authors contributed to the writing of this manuscript. Figures were provided by Sven G. Meuth.
Conflicts of Interest
The authors declare no conflict of interest.
Article information
Int J Mol Sci. 2015 Sep; 16(9): 21215–21236. Published online 2015 Sep 7. doi: 10.3390/ijms160921215 PMCID: PMC4613250 PMID: 26370960 Jay S. Coggan,1,* Stefan Bittner,2 Klaus M. Stiefel,1 Sven G. Meuth,2 and Steven A. Prescott3,4 Christoph Kleinschnitz, Academic Editor 1NeuroLinx Research Institute, La Jolla, CA 92039, USA; E-Mail: gro.xniloruen@sualk 2Department of Neurology, Institute of Physiology, Universitätsklinikum Münster, 48149 Münster, Germany; E-Mails: moc.kooltuo@renttib-nafets (S.B.); ed.retsneumku@htuem.nevs (S.G.M.) 3Neurosciences and Mental Health, the Hospital for Sick Children, Toronto, ON M5G 1X8, Canada; E-Mail: ac.sdikkcis@ttocserp.evets 4Department of Physiology and the Institute of Biomaterials and Biomedical Engineering, University of Toronto, Toronto, ON M5G 1X8, Canada
- Author to whom correspondence should be addressed; E-Mail: gro.xniloruen@yaj; Tel.: +1-858-243-6720.
Received 2015 May 26; Accepted 2015 Aug 25. Copyright © 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/). Articles from International Journal of Molecular Sciences are provided here courtesy of Multidisciplinary Digital Publishing Institute (MDPI)
Bibliography
- ↑ Virchow R. Uber das ausgebreitete Vorkommen einer dem Nervenmark analogen Substanz in den tierischen Geweben. Virchows Arch. Pathol. Anat. 1854;6:562–572. doi: 10.1007/BF02116709. [CrossRef] [Google Scholar]
- ↑ Stiefel K.M., Torben-Nielsen B., Coggan J.S. Proposed evolutionary changes in the role of myelin. Front. Neurosci. 2013;8 doi: 10.3389/fnins.2013.00202.[PMC free article] [PubMed] [CrossRef] [Google Scholar]
- ↑ Bullock T.H., Moore J.K., Fields R.D. Evolution of myelin sheaths: Both lamprey and hagfish lack myelin. Neurosci. Lett. 1984;48:145–148. doi: 10.1016/0304-3940(84)90010-7. [PubMed] [CrossRef] [Google Scholar]
- ↑ Davis A.D., Weatherby T.M., Hartline D.K., Lenz P.H. Myelin-like sheaths in copepod axons. Nature. 1999;398:571–571. doi: 10.1038/19212. [PubMed] [CrossRef] [Google Scholar]
- ↑ Hartline D.K., Colman D.R. Rapid conduction and the evolution of giant axons and myelinated fibers. Curr. Biol. 2007;17:R29–R35. doi: 10.1016/j.cub.2006.11.042. [PubMed] [CrossRef] [Google Scholar]
- ↑ Arancibia-Carcamo I.L., Attwell D. The node of ranvier in CNS pathology. Acta Neuropathol. 2014;128:161–175. doi: 10.1007/s00401-014-1305-z.[PMC free article] [PubMed] [CrossRef] [Google Scholar]
- ↑ Faisal A.A., White J.A., Laughlin S.B. Ion-channel noise places limits on the miniaturization of the brain’s wiring. Curr. Biol. 2005;15:1143–1149. doi: 10.1016/j.cub.2005.05.056. [PubMed] [CrossRef] [Google Scholar]
- ↑ Babbs C.F., Riyi S. Subtle paranodal injury slows impulse conduction in a mathematical model of myelinated axons. PLoS ONE. 2013;8:e67767. doi: 10.1371/journal.pone.0067767. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
- ↑ 9.0 9.1 9.2 Trapp B.D., Nave K.A. Multiple sclerosis: An immune or neurodegenerative disorder? Annu. Rev. Neurosci. 2008;31:247–69. doi: 10.1146/annurev.neuro.30.051606.094313. [PubMed] [CrossRef] [Google Scholar]
- ↑ 10.0 10.1 10.2 10.3 Compston A., Coles A. Multiple sclerosis. Lancet. 2008;372:1502–1517. doi: 10.1016/S0140-6736(08)61620-7. [PubMed] [CrossRef] [Google Scholar]
- ↑ Ostermann P.O., Westerberg C.E. Paroxysmal attacks in multiple sclerosis. Brain. 1975;98:189–202. doi: 10.1093/brain/98.2.189. [PubMed] [CrossRef] [Google Scholar]
- ↑ Twomey J.A., Espir M.L. Paroxysmal symptoms as the first manifestations of multiple sclerosis. J. Neurol. Neurosurg. Psychiatry. 1980;43:296–304. doi: 10.1136/jnnp.43.4.296. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
- ↑ Seewann A., Vrenken H., van der Valk P., Blezer E.L., Knol D.L., Castelijns J.A., Polman C.H., Pouwels P.J., Barkhof F., Geurts J.J. Diffusely abnormal white matter in chronic multiple sclerosis: Imaging and histopathologic analysis. Arch. Neurol. 2009;66:601–609. doi: 10.1001/archneurol.2009.57. [PubMed] [CrossRef] [Google Scholar]
- ↑ Ceccarelli A., Bakshi R., Neema M. MRI in multiple sclerosis: A review of the current literature. Curr. Opin. Neurol. 2012;25:402–409. doi: 10.1097/WCO.0b013e328354f63f. [PubMed] [CrossRef] [Google Scholar]
- ↑ 15.0 15.1 Moore J.W., Joyner R.W., Brill M.H., Waxman S.D., Najar-Joa M. Simulations of conduction in uniform myelinated fibers. Relative sensitivity to changes in nodal and internodal parameters. Biophys. J. 1978;21:147–160. doi: 10.1016/S0006-3495(78)85515-5. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
- ↑ Waxman S.G., Kocsis J.D., Stys P.K. The Axon: Structure, Function and Pathophysiology. Oxford University Press; New York, NY, USA: 1995. [Google Scholar]
- ↑ Polman C.H., Reingold S.C., Banwell B., Clanet M., Cohen J.A., Filippi M., Fujihara K., Havrdova E., Hutchinson M., Kappos L., et al. Diagnostic criteria for multiple sclerosis: 2010 revisions to the McDonald criteria. Ann. Neurol. 2011;69:292–302. doi: 10.1002/ana.22366. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
- ↑ 18.0 18.1 Stephanova D.I., Dimitrov B. Computational Neuroscience: Simulated Demyelinating Neuropathies and Neuronopathies. CRC Press; Boca Raton, FL, USA: 2013. [Google Scholar]
- ↑ 19.0 19.1 Bostock H., Baker M., Reid G. Changes in excitability of human motor axons underlying post-ischaemic fasciculations: Evidence for two stable states. J. Physiol. 1991;441:537–557. doi: 10.1113/jphysiol.1991.sp018766.[PMC free article] [PubMed] [CrossRef] [Google Scholar]
- ↑ Mogyoros I., Kiernan M.C., Burke D., Bostock H. Strength-duration properties of sensory and motor axons in amyotrophic lateral sclerosis. Brain. 1998;121:851–859. doi: 10.1093/brain/121.5.851. [PubMed] [CrossRef] [Google Scholar]
- ↑ 21.0 21.1 Kiernan M.C., Burke D., Andersen K.V., Bostock H. Multiple measures of axonal excitability: A new approach in clinical testing. Muscle Nerve. 2000;23:399–409. doi: 10.1002/(SICI)1097-4598(200003)23:3<399::AID-MUS12>3.0.CO;2-G. [PubMed] [CrossRef] [Google Scholar]
- ↑ Cappelen-Smith C., Kuwabara S., Lin C.S., Mogyoros I., Burke D. Membrane properties in chronic inflammatory demyelinating polyneuropathy. Brain. 2001;124:2439–2447. doi: 10.1093/brain/124.12.2439. [PubMed] [CrossRef] [Google Scholar]
- ↑ Kuwabara S., Ogawara K., Sung J.Y., Mori M., Kanai K., Hattori T., Yuki N., MLin C.S., Burke D., Bostock H. Differences in membrane properties of axonal and demyelinating Guillain-Barré syndromes. Ann. Neurol. 2002;52:180–187. doi: 10.1002/ana.10275. [PubMed] [CrossRef] [Google Scholar]
- ↑ Nodera H., Bostock H., Kuwabara S., Sakamoto T., Asanuma K., Jia-Ying S., Ogawara K., Hattori N., Hirayama M., Sobue G., et al. Nerve excitability properties in Charcot-Marie-Tooth disease type 1A. Brain. 2004;127:203–211. doi: 10.1093/brain/awh020. [PubMed] [CrossRef] [Google Scholar]
- ↑ Sung M.H., Simon R. In silico simulation of inhibitor drug effects on nuclear factor-κB pathway dynamics. Mol. Pharmacol. 2004;66:70–75. doi: 10.1124/mol.66.1.70. [PubMed] [CrossRef] [Google Scholar]
- ↑ Stephanova D.I., Daskalova M. Differences in potentials and excitability properties in simulated cases of demyelinating neuropathies. Part III. Paranodal internodal demyelination. Clin. Neurophysiol. 2005;116:2334–2341. doi: 10.1016/j.clinph.2005.07.013. [PubMed] [CrossRef] [Google Scholar]
- ↑ Stephanova D.I., Daskalova M.S. Differences between the channels, currents and mechanisms of conduction slowing/block and accommodative processes in simulated cases of focal demyelinating neuropathies. Eur. Biophys. J. 2008;37:829–842. doi: 10.1007/s00249-008-0284-1. [PubMed] [CrossRef] [Google Scholar]
- ↑ Stephanova D.I., Alexandrov A.S. Simulating mild systematic and focal demyelinating neuropathies: Membrane property abnormalities. J. Integr. Neurosci. 2006;5:595–623. doi: 10.1142/S0219635206001331. [PubMed] [CrossRef] [Google Scholar]
- ↑ Stephanova D.I., Daskalova M., Alexandrov A.S. Channels, currents and mechanisms of accommodative processes in simulated cases of systematic demyelinating neuropathies. Brain Res. 2007;1171:138–151. doi: 10.1016/j.brainres.2007.07.029. [PubMed] [CrossRef] [Google Scholar]
- ↑ 30.0 30.1 Stephanova D.I., Krustev S.M., Negrev N., Daskalova M. The myelin sheath aqueous layers improve the membrane properties of simulated chronic demyelinating neuropathies. J. Integr. Neurosci. 2011;10:105–120. doi: 10.1142/S0219635211002646. [PubMed] [CrossRef] [Google Scholar]
- ↑ Stephanova D.I., Alexandrov A.S., Kossev A., Christova L. Simulating focal demyelinating neuropathies: Membrane property abnormalities. Biol. Cybern. 2007;96:195–208. doi: 10.1007/s00422-006-0113-5. [PubMed] [CrossRef] [Google Scholar]
- ↑ Bø L., Geurts J.J., Mörk S.J., van der Valk P. Grey matter pathology in multiple sclerosis. Acta Neurol. Scand. Suppl. 2006;183:48–50. doi: 10.1111/j.1600-0404.2006.00615.x. [PubMed] [CrossRef] [Google Scholar]
- ↑ Geurts J.J., Barkhof F. Grey matter pathology in multiple sclerosis. Lancet Neurol. 2008;7:841–851. doi: 10.1016/S1474-4422(08)70191-1. [PubMed] [CrossRef] [Google Scholar]
- ↑ Zivadinov R., Pirko I. Advances in understanding gray matter pathology in multiple sclerosis: Are we ready to redefine disease pathogenesis? BMC Neurol. 2012;12 doi: 10.1186/1471-2377-12-9. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
- ↑ Popescu B.F., Lucchinetti C.F. Pathology of demyelinating diseases. Annu. Rev. Pathol. 2012;7:185–217. doi: 10.1146/annurev-pathol-011811-132443.[PubMed] [CrossRef] [Google Scholar]
- ↑ Kurtzke J.F., Beebe G.W., Nagler B., Nefzger M.D., Auth T.L., Kurland L.T. Studies on the natural history of multiple sclerosis: V. Long-term survival in young men. Arch. Neurol. 1970;22:215–225. doi: 10.1001/archneur.1970.00480210025003. [PubMed] [CrossRef] [Google Scholar]
- ↑ Rao S.M., Leo G.J., Bernardin L., Unverzagt F. Cognitive dysfunction in multiple sclerosis. I. Frequency, patterns, and prediction. Neurology. 1991;41:685–691. doi: 10.1212/WNL.41.5.685. [PubMed] [CrossRef] [Google Scholar]
- ↑ Meuth S.G., Bittner S., Ulzheimer J.C., Kleinschnitz C., Kieseier B.C., Wiendl H. Therapeutic approaches to multiple sclerosis: An update on failed, interrupted, or inconclusive trials of neuroprotective and alternative treatment strategies. BioDrugs. 2010;24:317–330. doi: 10.2165/11537190-000000000-00000. [PubMed] [CrossRef] [Google Scholar]
- ↑ Goldenberg M.M. Multiple sclerosis review. Pharm. Ther. 2012;37:137–139.[PMC free article] [PubMed] [Google Scholar]
- ↑ Göbel K., Wedell J.H., Herrmann A.M., Wachsmuth L., Pankratz S., Bittner S., Budde T., Kleinschnitz C., Faber C., Wiendl H., et al. 4-Aminopyridine ameliorates mobility but not disease course in an animal model of multiple sclerosis. Exp. Neurol. 2013;248:62–71. doi: 10.1016/j.expneurol.2013.05.016.[PubMed] [CrossRef] [Google Scholar]
- ↑ Krishnan A.V., Kiernan M.C. Sustained-release fampridine and the role of ion channel dysfunction in multiple sclerosis. Mult. Scler. 2013;19:385–391. doi: 10.1177/1352458512463769. [PubMed] [CrossRef] [Google Scholar]
- ↑ Bowe C.M., Kocsis J.D., Targ E.F., Waxman S.G. Physiological effects of 4-aminopyridine on demyelinated mammalian motor and sensory fibers. Ann. Neurol. 1987;22:264–268. doi: 10.1002/ana.410220212. [PubMed] [CrossRef] [Google Scholar]
- ↑ Sakurai M., Kanazawa I. Positive symptoms in multiple sclerosis: Their treatment with sodium channel blockers, lidocaine and mexiletine. J. Neurol. Sci. 1999;162:162–168. doi: 10.1016/S0022-510X(98)00322-0. [PubMed]
- ↑ Mattson M.P., Guthrie P.B., Kater S.B. A role for Na+-dependent Ca2+extrusion in protection against neuronal excitotoxicity. FASEB J. 1989;3:2519–2526. [PubMed] [Google Scholar]
- ↑ Moll N.M., Rietsch A.M., Thomas S., Ransohoff A.J., Lee J.C., Fox R., Chang A., Ransohoff R.M., Fisher E. Multiple sclerosis normal-appearing white matter: Pathology-imagig correlations. Ann. Neurol. 2011;70:764–773. doi: 10.1002/ana.22521. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
- ↑ 46.0 46.1 Lucchinetti C., Brück W., Parisi J., Scheithauer B., Rodriguez M., Lassmann H. Heterogeneity of multiple sclerosis lesions: Implications for the pathogenesis of demyelination. Ann. Neurol. 2000;47:707–717. doi: 10.1002/1531-8249(200006)47:6<707::AID-ANA3>3.0.CO;2-Q. [PubMed] [CrossRef] [Google Scholar]
- ↑ Kassmann C.M., Nave K.A. Oligodendroglial impact on axonal function and survival— A hypothesis. Curr. Opin. Neurol. 2008;21:235–241. doi: 10.1097/WCO.0b013e328300c71f. [PubMed] [CrossRef] [Google Scholar]
- ↑ Scolding N., Franklin R. Axon loss in multiple sclerosis. Lancet. 1998;352:340–341. doi: 10.1016/S0140-6736(05)60463-1. [PubMed] [CrossRef] [Google Scholar]
- ↑ Mi S., Miller R.H., Lee X., Scott M.L., Shulag-Morskaya S., Shao Z., Chang J., Thill G., Levesque M., Zhang M., et al. LINGO-1 negatively regulates myelination by oligodendrocytes. Nat. Neurosci. 2005;8:745–751. doi: 10.1038/nn1460. [PubMed] [CrossRef] [Google Scholar]
- ↑ Bittner S., Ruck T., Schuhmann M.K., Herrmann A.M., Maati H.M., Bobak N., Göbel K., Langhauser F., Stegner D., Ehling P., et al. 2013 Endothelial TWIK-related potassium channel-1 (TREK1) regulates immune-cell trafficking into the CNS. Nat. Med. 2013;19:1161–1165. doi: 10.1038/nm.3303. [PubMed]
- ↑ Viglietta V., Baecher-Allan C., Weiner H.L., Hafler D.A. Loss of functional suppression by CD4+CD25+ regulatory T cells in patients with multiple sclerosis. J. Exp. Med. 2004;199:971–999. doi: 10.1084/jem.20031579.[PMC free article] [PubMed] [CrossRef] [Google Scholar]
- ↑ Zajicek J.P., Wing M., Scolding N.J., Compston D.A. Interactions between oligodendrocytes and microglia. A major role for complement and tumour necrosis factor in oligodendrocyte adherence and killing. Brain. 1992;115:1611–1631. [PubMed] [Google Scholar]
- ↑ 53.0 53.1 53.2 Nikić I., Merkler D., Sorbara C., Brinkoetter M., Kreutzfeldt M., Bareyre F.M., Brück W., Bishop D., Misgeld T., Kerschensteiner M. A reversible form of axon damage in experimental autoimmune encephalomyelitis and multiple sclerosis. Nat. Med. 2011;17:495–499. doi: 10.1038/nm.2324. [PubMed] [CrossRef] [Google Scholar]
- ↑ Barnett M.H., Prineas J.W. Relapsing and remitting multiple sclerosis: Pathology of the newly forming lesion. Ann. Neurol. 2004;55:458–468. doi: 10.1002/ana.20016. [PubMed] [CrossRef] [Google Scholar]
- ↑ Van der Laan L.J., Ruuls S.R., Weber K.S., Lodder I.J., Döpp E.A., Dijkstra C.D. Macrophage phagocytosis of myelin in vitro determined by flow cytometry: Phagocytosis is mediated by CR3 and induces production of tumor necrosis factor-α and nitric oxide. J. Neuroimmunol. 1996;70:145–152. doi: 10.1016/S0165-5728(96)00110-5. [PubMed] [CrossRef] [Google Scholar]
- ↑ Wang G., Thompson S.M. Maladaptive homeostatic plasticity in a rodent model of central pain syndrome: Thalamic hyperexcitability after spinothalamic tract lesions. J. Neurosci. 2008;28:11959–11969. doi: 10.1523/JNEUROSCI.3296-08.2008. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
- ↑ 57.0 57.1 Coggan J.S., Prescott S.A., Bartol T.M., Sejnowski T.J. Imbalance of ionic conductances contributes to diverse symptoms of demyelination. Proc. Natl. Acad. Sci. USA. 2010;107:20602–20609. doi: 10.1073/pnas.1013798107.[PMC free article] [PubMed] [CrossRef] [Google Scholar]
- ↑ 58.0 58.1 Coggan J.S., Ocker G.K., Sejnowski T.J., Prescott S.A. Explaining pathological changes in axonal excitability through dynamical analysis of conductance-based models. J. Neural Eng. 2011;8 doi: 10.1088/1741-2560/8/6/065002. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
- ↑ 59.0 59.1 59.2 Coggan J.S., Prescott S.A., Sejnowski T.J. Cooperativity between remote sites of ectopic spiking allows afterdischarge to be initiated and maintained at different locations. J. Comput. Neurosci. 2015;39:17–28. doi: 10.1007/s10827-015-0562-8. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
- ↑ 60.0 60.1 Aon M.A., Cortassa S., Akar F.G., Brown D.A., Zhou L., O’Rourke B. From mitochondrial dynamics to arrhythmias. Int. J. Biochem. Cell Biol. 2009;41:1940–1948. doi: 10.1016/j.biocel.2009.02.016. [PMC free article][PubMed] [CrossRef] [Google Scholar]
- ↑ 61.0 61.1 Su K., Bourdette D., Forte M. Mitochondrial dysfunction and neurodegeneration in multiple sclerosis. Front. Physiol. 2013;4doi: 10.3389/fphys.2013.00169. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
- ↑ Soltesz I., Staley K. Computational Neuroscience in Epilepsy. 1st ed. Elsevier; London, UK: 2008. [Google Scholar]
- ↑ Hodgkin A.L., Huxley A.F. The components of membrane conductance in the giant axon of Loligo. J. Physiol. 1952;116:473–496. doi: 10.1113/jphysiol.1952.sp004718. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
- ↑ Hodgkin A.L., Huxley A.F. Currents carried by sodium and potassium ions through the membrane of the giant axon of Loligo. J. Physiol. 1952;116:449–472. doi: 10.1113/jphysiol.1952.sp004717. [PMC free article] [PubMed]
- ↑ Fitzhugh R. Computation of impulse initiation and saltatory conduction in a myelinated nerve fiber. Biophys. J. 1962;2:11–21. doi: 10.1016/S0006-3495(62)86837-4. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
- ↑ Goldman L., Albus J.S. Computation of impulse conduction in myelinated fibers; theoretical basis of the velocity-diameter relation. Biophys. J. 1968;8:596–607. doi: 10.1016/S0006-3495(68)86510-5. [PMC free article][PubMed] [CrossRef] [Google Scholar]
- ↑ Frankenhaeuser B., Huxley A.F. The action potential in the myelinated nerve fiber of Xenopus laevis as computed on the basis of voltage clamp data. J. Physiol. 1964;171:302–315. doi: 10.1113/jphysiol.1964.sp007378.[PMC free article] [PubMed] [CrossRef] [Google Scholar]
- ↑ Smith R.S., Koles Z.J. Myelinated nerve fibers: Computed effect of myelin thickness on conduction velocity. Am. J. Physiol. 1970;219:1256–1258.[PubMed] [Google Scholar]
- ↑ Hutchinson N.A., Koles Z.J., Smith R.S. Conduction velocity in myelinated nerve fibres of Xenopus laevis. J. Physiol. 1970;208:279–289. doi: 10.1113/jphysiol.1970.sp009119. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
- ↑ Koles Z.J., Rasminsky M. A computer simulation of conduction in demyelinated nerve fibres. J. Physiol. 1972;227:351–364. doi: 10.1113/jphysiol.1972.sp010036. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
- ↑ Hardy W.L. Propagation speed in myelinated nerve. II. Theoretical dependence on external Na and on temperature. Biophys. J. 1973;13:1071–1089. doi: 10.1016/S0006-3495(73)86046-1. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
- ↑ Schauf C.L., Davis F.A. Impulse conduction in multiple sclerosis: A theoretical basis for modification by temperature and pharmacological agents. J. Neurol. Neurosurg. Psychiatry. 1974;37:152–161. doi: 10.1136/jnnp.37.2.152.[PMC free article] [PubMed] [CrossRef] [Google Scholar]
- ↑ Brill M.H., Waxman S.G., Moore J.W., Joyner R.W. Conduction velocity and spike configuration in myelinated fibres: Computed dependence on internode distance. J. Neurol. Neurosurg. Psychiatry. 1977;40:769–774. doi: 10.1136/jnnp.40.8.769. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
- ↑ Waxman S.G., Brill M.H. Conduction through demyelinated plaques in multiple sclerosis: Computer simulations of facilitation by short internodes. J. Neurol. Neurosurg. Psychiatry. 1978;41:408–416. doi: 10.1136/jnnp.41.5.408.[PMC free article] [PubMed] [CrossRef] [Google Scholar]
- ↑ Wood S.L., Waxman S.G., Kocsis J.D. Conduction of trans of impulses in uniform myelinated fibers: Computed dependence on stimulus frequency. Neuroscience. 1982;7:423–430. doi: 10.1016/0306-4522(82)90276-7. [PubMed] [CrossRef] [Google Scholar]
- ↑ Goldfinger M.D. Computation of high safety factor impulse propagation at axonal branch points. Neuroreport. 2000;11:449–456. doi: 10.1097/00001756-200002280-00005. [PubMed] [CrossRef] [Google Scholar]
- ↑ 77.0 77.1 Blight A.R. Computer simulation of action potentials and afterpotentials in mammalian myelinated axons: The case for a lower resistance myelin sheath. Neuroscience. 1985;15:13–31. doi: 10.1016/0306-4522(85)90119-8. [PubMed] [CrossRef] [Google Scholar]
- ↑ 78.0 78.1 Halter J.A., Clark J.W., Jr. A distributed-parameter model of the myelinated nerve fiber. J. Theor. Biol. 1991;148:345–382. doi: 10.1016/S0022-5193(05)80242-5. [PubMed] [CrossRef] [Google Scholar]
- ↑ Schwarz J.R., Eikhof G. Na currents and action potentials in rat myelinated nerve fibres at 20 and 37 °C. Pflugers Arch. 1987;409:569–577. doi: 10.1007/BF00584655. [PubMed] [CrossRef] [Google Scholar]
- ↑ 80.0 80.1 Stephanova D.I. Myelin as longitudinal conductor: A multi-layered model of the myelinated human motor nerve fibre. Biol. Cybern. 2001;84:301–308. doi: 10.1007/s004220000213. [PubMed] [CrossRef] [Google Scholar]
- ↑ 81.0 81.1 McIntyre C.C., Richardson A.G., Grill W.M. Modeling the excitability of mammalian nerve fibers: Influence of afterpotentials on the recovery cycle. J. Neurophysiol. 2002;87:995–1006. [PubMed] [Google Scholar]
- ↑ 82.0 82.1 Einziger P.D., Livshitz L.M., Mizrahi J. Generalized cable equation model for myelinated nerve fiber. IEEE Trans. Biomed. Eng. 2005;52:1632–1642. doi: 10.1109/TBME.2005.856031. [PubMed] [CrossRef] [Google Scholar]
- ↑ Volman V., Ng L. Primary paranode demyelination modulates slowly developing axonal depolarization in a model of axonal injury. J. Neural Comput. 2014;37:439–457. [PubMed] [Google Scholar]
- ↑ Stephanova D.I., Bostock H. A Distributed-parameter model of the myelinated human motor nerve fibre: Temporal and spatial distributions of action potentials and ionic currents. Biol. Cybern. 1995;73:275–280. doi: 10.1007/BF00201429. [PubMed] [CrossRef] [Google Scholar]
- ↑ Chiu S.Y., Ritchie J.M. On the physiological role of internodal potassium channels and the security of conduction in myelinated nerve fibres. Proc. R. Soc. Lond. B Biol. Sci. 1984;220:415–422. doi: 10.1098/rspb.1984.0010.[PubMed] [CrossRef] [Google Scholar]
- ↑ Brismar T., Schwarz J.R. Potassium permeability in rat myelinated nerve fibres. Acta Physiol. Scand. 1985;124:141–148. doi: 10.1111/j.1748-1716.1985.tb07645.x. [PubMed] [CrossRef] [Google Scholar]
- ↑ Chiu S.Y., Schwarz W. Sodium and potassium currents in acutely demyelinated internodes of rabbit sciatic nerves. J. Physiol. 1987;391:631–649. doi: 10.1113/jphysiol.1987.sp016760. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
- ↑ Baker M., Bostock H., Grafe P., Martius P. Function and distribution of three types of rectifying channel in rat spinal root myelinated axons. J. Physiol. 1987;383:45–67. [PMC free article] [PubMed] [Google Scholar
- ↑ Röper J., Schwarz J.R. Heterogeneous distribution of fast and slow potassium channels in myelinated rat nerve fibres. J. Physiol. 1989;416:93–110. doi: 10.1113/jphysiol.1989.sp017751. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
- ↑ Bittner S., Meuth S.G. Targeting ion channels for the treatment of autoimmune neuroinflammation. Ther. Adv. Neurol. Disord. 2013;6:322–336. doi: 10.1177/1756285613487782. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
- ↑ Waxman S.G., Ritchie J.M. Molecular dissection of the myelinated axon. Ann. Neurol. 1993;33:121–136. doi: 10.1002/ana.410330202. [PubMed] [CrossRef] [Google Scholar]
- ↑ Bittner S., Budde T., Wiendl H., Meuth S.G. From the background to the spotlight: TASK channels in pathological conditions. Brain Pathol. 2010;20:999–1009. doi: 10.1111/j.1750-3639.2010.00407.x. [PMC free article][PubMed] [CrossRef] [Google Scholar]
- ↑ Ehling P., Bittner S., Budde T., Wiendl H., Meuth S.G. Ion channels in autoimmune neurodegeneration. FEBS Lett. 2011;585:3836–3842. doi: 10.1016/j.febslet.2011.03.065. [PubMed] [CrossRef] [Google Scholar]
- ↑ 94.0 94.1 Hübel N., Dahlem M.A. Dynamics from seconds to hours in Hodgkin-Huxley model with time-dependent ion concentrations and buffer reservoirs. PLoS Comput. Biol. 2014;10:e1003941. doi: 10.1371/journal.pcbi.1003941.[PMC free article] [PubMed] [CrossRef] [Google Scholar]
- ↑ Ganapathy L., Clark J.W. Extracellular currents and potentials of the active myelinated nerve fibre. Biophys. J. 1987;52:749–761. doi: 10.1016/S0006-3495(87)83269-1. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
- ↑ Prescott S.A. Pathological changes in peripheral nerve excitability. In: Jaeger D., Jung R., editors. Encyclopedia of Computational Neurosci. 1st ed. Springer-Verlag; New York, NY, USA: 2015. [Google Scholar]
- ↑ Barrett E.F., Barrett J.N. Intracellular recording from vertebrate myelinated axons: Mechanism of the depolarizing afterpotential. J. Physiol. 1982;323:117–144. doi: 10.1113/jphysiol.1982.sp014064. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
- ↑ Blight A.R., Someya S. Depolarizing afterpotentials in myelinated axons of mammalian spinal cord. Neuroscience. 1985;15:1–12. doi: 10.1016/0306-4522(85)90118-6. [PubMed] [CrossRef] [Google Scholar]
- ↑ Richardson A.G., McIntyre C.C., Grill W.M. Modelling the effects of electric fields on nerve fibres: Influence of the myelin sheath. Med. Biol. Eng. Comput. 2000;38:438–446. doi: 10.1007/BF02345014. [PubMed] [CrossRef] [Google Scholar]
- ↑ Zlochiver S. Persistent reflection underlies ectopic activity in multiple sclerosis: A numerical study. Biol. Cybern. 2010;102:181–196. doi: 10.1007/s00422-009-0361-2. [PubMed] [CrossRef] [Google Scholar]
- ↑ Ratté S., Zhu Y., Lee K.Y., Prescott S.A. Criticality and degeneracy in injury-induced changes in primary afferent excitability and the implications for neuropathic pain. Elife. 2014;3:e02370. doi: 10.7554/eLife.02370.[PMC free article] [PubMed] [CrossRef] [Google Scholar]
- ↑ Zhu Y., Feng B., Schwartz E.S., Gebhart G.F., Prescott S.A. Novel method to assess axonal excitability using channelrhodopsin-based photoactivation. J. Neurophysiol. 2015;113:2242–2249. doi: 10.1152/jn.00982.2014.[PMC free article] [PubMed] [CrossRef] [Google Scholar]
- ↑ Tagoe T., Barker M., Jones A., Allcock N., Hamann M. Auditory nerve perinodal dysmyelination in noise-induced hearing loss. J. Neurosci. 2014;12:2684–2688. doi: 10.1523/JNEUROSCI.3977-13.2014.
- ↑ Brown A.M., Hamann M. Computational modeling of the effects of auditory nerve dysmyelination. Front. Neuroanat. 2014;8doi: 10.3389/fnana.2014.00073. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
- ↑ Stephanova D.I., Daskalova M. Electrotonic potentials in simulated chronic inflammatory demyelinating polyneuropathy at 20 °C–42 °C. J. Integr. Neurosci. 2015;27:1–18. doi: 10.1142/S0219635215500119. [PubMed] [CrossRef] [Google Scholar]
- ↑ Rasminsky M. Hyperexcitability of pathologically myelinated axons and positive symptoms in multiple sclerosis. Adv. Neurol. 1981;31:289–297.[PubMed] [Google Scholar]
- ↑ Ulrich J., Groebke-Lorenz W. The optic nerve in multiple sclerosis: A morphological study with retrospective clinicopathological correlation. Neuro-Ophthalmology. 1983;3:149–159. doi: 10.3109/01658108309009732.[CrossRef] [Google Scholar]
- ↑ Hamada M.S., Kole M.H. Myelin loss and axonal ion channel adaptations associated with gray matter neuronal hyperexcitability. J. Neurosci. 2015;35:7272–7786. [PMC free article] [PubMed] [Google Scholar]
- ↑ Yu N., Morris C.E., Joós B., Longtin A. Spontaneous excitation patterns computed for axons with injury-like impairments of sodium channels and Na/K pumps. PLoS Comput. Biol. 2012;8:e1002664. doi: 10.1371/journal.pcbi.1002664. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
- ↑ Lopreore C.L., Bartol T.M., Coggan J.S., Keller D.X., Sosinsky G.E., Ellisman M.H., Sejnowski T.J. Computational modeling of three-dimensional electrodiffusion in biological systems: Application to the node of Ranvier. Biophys. J. 2008;95:2624–2635. doi: 10.1529/biophysj.108.132167.
- ↑ Broome T.M., Cole.man R.A. A mathematical model of cell death in multiple sclerosis. J. Neurosci. Methods. 2011;201:420–425. doi: 10.1016/j.jneumeth.2011.08.008. [PubMed] [CrossRef] [Google Scholar]
- ↑ Ridsdale R.A., Beniac D.R., Tompkins T.A., Moscarello M.A., Harauz G. Three-dimensional structure of myelin basic protein. II. Molecular modeling and considerations of predicted structures in multiple sclerosis. J. Biol. Chem. 1997;272:4269–4275. doi: 10.1074/jbc.272.7.4269. [PubMed] [CrossRef] [Google Scholar]
- ↑ Pigozzo A.B., Macedo G.C., Santos R.W., Lobosco M. On the computational modeling of the innate immune system. BMC Bioinform. 2013;14 doi: 10.1186/1471-2105-14-S6-S7. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
- ↑ Doerck S., Göbel K., Weise G., Schneider-Hohendorf T., Reinhardt M., Hauff P., Schwab N., Linker R., Mäurer M., Meuth S.G., et al. Temporal pattern of ICAM-I mediated regulatory T cell recruitment to sites of inflammation in adoptive transfer model of multiple sclerosis. PLoS ONE. 2010;5:e15478. doi: 10.1371/journal.pone.0015478. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
- ↑ De Mendizábal N.V., Carneiro J., Solé R.V., Goñi J., Bragard J., Martinez-Forero I., Martinez-Pasamar S., Sepulcre J., Torrealdea J., Bagnato F., et al. Modeling the effector-regulatory T cell cross-regulation reveals the intrinsic character of relapses in Multiple Sclerosis. BMC Syst. Biol. 2011;5doi: 10.1186/1752-0509-5-114. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
- ↑ Jolivet R., Coggan J.S., Allaman I., Magistretti P.J. Multi-timescale modeling of activity-dependent metabolic coupling in the neuron-glia-vasculature ensemble. PLoS Comput. Biol. 2015;11:e1004036. doi: 10.1371/journal.pcbi.1004036. [PMC free article] [PubMed] [CrossRef]
- ↑ Zeis T., Allaman I., Gentner M., Schroder K., Tschopp J., Magistretti P.J., Schaeren-Wiemers N. Metabolic gene expression changes in astrocytes in Multiple Sclerosis cerebral cortex are indicative of immune-mediated signaling. Brain Behav. Immun. 2015;48:315–325. doi: 10.1016/j.bbi.2015.04.013.[PubMed] [CrossRef] [Google Scholar]








