Difference between revisions of "Store:ACincisivo"
| Line 49: | Line 49: | ||
|Laterale | |Laterale | ||
|} | |} | ||
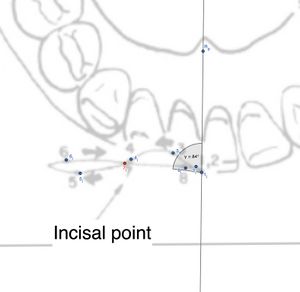
<br />Anche in questo | <br />Anche in questo caso abbiamo tre punti nel piano 2D di interesse di coordinate {{Tooltip|2=<math>P1_{i}</math> del punto 1 dell'incisivo sul lato lavorante: <math>(631.5, -1151.8)</math>, Coordinate <math>P7_{i}</math> del punto 7 dell'incisivo sul lato lavorante: <math>(509.6, -1139.9)</math>, Coordinate <math>H3_{i}</math> del punto di riferimento dell'incisivo sul lato lavorante: <math>(634.2, -921)</math>.|3=2}} Questi punti rappresentano posizioni specifiche all'interno di un sistema articolare che stiamo studiando. L'obiettivo è calcolare l'angolo tra il segmento che unisce i punti <math>P1_{i}</math> e <math>P7_{i}</math> e il segmento che unisce i punti <math>P1_{i}</math> e <math>R_p</math>. Questo metodo è utile per determinare la relazione angolare tra due movimenti distinti nello spazio per cui come precedentemente si descrive il calcolo dei vettori {{Tooltip|2=Il vettore tra il punto <math>P1_{i}</math> e il punto <math>P7_{i}</math>: <math>\vec{AB} = P7_{i} - P1_{i} = (509.6, -1139.9) - (631.5, -1151.8) = (-121.9, 11.9)</math>, Il vettore tra il punto 1<sub>Lm</sub> e il punto H₃: <math>\vec{AC} = H3_{i} - P1_{i} = (634.2, -921) - (631.5, -1151.8) = (2.7, 230.8)</math>. Prodotto scalare: Il prodotto scalare tra i vettori <math>\vec{AB}</math> e <math>\vec{AC}</math> è dato dalla formula: <math>\vec{AB} \cdot \vec{AC} = AB_x \cdot AC_x + AB_y \cdot AC_y</math>, e sostituendo i valori calcolati: <math>\vec{AB} \cdot \vec{AC} = (-121.9) \cdot (2.7) + (11.9) \cdot (230.8) = -329.13 + 2746.52 = 2417.39</math>. Calcolo delle norme: Le norme (lunghezze) dei due vettori sono calcolate con la formula della lunghezza del vettore: <math>|\vec{AB}| = \sqrt{AB_x^2 + AB_y^2} = \sqrt{(-121.9)^2 + (11.9)^2} = \sqrt{15004.02} \approx 122.48</math> e <math>|\vec{AC}| = \sqrt{AC_x^2 + AC_y^2} = \sqrt{53275.93} \approx 230.85</math>|3=2}} e della norma{{Tooltip|2=Le norme (lunghezze) dei due vettori sono calcolate con la formula della lunghezza del vettore:<math> | ||
|\vec{AB}| = \sqrt{AB_x^2 + AB_y^2} = \sqrt{(-121.9)^2 + (11.9)^2} = \sqrt{14862.41 + 141.61} = \sqrt{15004.02} \approx 122.48</math><math>|\vec{AC}| = \sqrt{AC_x^2 + AC_y^2} = \sqrt{(2.7)^2 + (230.8)^2} = \sqrt{7.29 + 53268.64} = \sqrt{53275.93} \approx 230.85 | |\vec{AB}| = \sqrt{AB_x^2 + AB_y^2} = \sqrt{(-121.9)^2 + (11.9)^2} = \sqrt{14862.41 + 141.61} = \sqrt{15004.02} \approx 122.48</math><math>|\vec{AC}| = \sqrt{AC_x^2 + AC_y^2} = \sqrt{(2.7)^2 + (230.8)^2} = \sqrt{7.29 + 53268.64} = \sqrt{53275.93} \approx 230.85 | ||
</math>}} per giungere alla definizione del coseno dell'angolo tra i due vettori | </math>}} per giungere alla definizione del coseno dell'angolo tra i due vettori | ||
Revision as of 17:09, 7 December 2024
Incisal
Il paragrafo caricato descrive un'analisi matematica dei movimenti articolari dell'incisivo sul lato lavorante. Utilizzando le coordinate di tre punti nello spazio 2D (P1, P7 e H₃), vengono calcolate le distanze lineari tra i punti, oltre all'angolo tra i segmenti che collegano questi punti.
| Punto | Distanza (mm) | Direzione in X
(antero-posteriore) |
Direzione in Y
(latero-mediale) |
|---|---|---|---|
| 2 | 2.34 | Indietro | Laterale |
| 3 | 4.57 | Indietro | Laterale |
| 4 | 10.96 | Indietro | Laterale |
| 5 | 20.28 | Indietro | Laterale |
| 6 | 21.80 | Indietro | Laterale |
| 7* | 13.84 | Indietro | Laterale |
| 8 | 2.64 | Indietro | Laterale |
Anche in questo caso abbiamo tre punti nel piano 2D di interesse di coordinate ![]() del punto 1 dell'incisivo sul lato lavorante: , Coordinate del punto 7 dell'incisivo sul lato lavorante: , Coordinate del punto di riferimento dell'incisivo sul lato lavorante: . Questi punti rappresentano posizioni specifiche all'interno di un sistema articolare che stiamo studiando. L'obiettivo è calcolare l'angolo tra il segmento che unisce i punti e e il segmento che unisce i punti e . Questo metodo è utile per determinare la relazione angolare tra due movimenti distinti nello spazio per cui come precedentemente si descrive il calcolo dei vettori
del punto 1 dell'incisivo sul lato lavorante: , Coordinate del punto 7 dell'incisivo sul lato lavorante: , Coordinate del punto di riferimento dell'incisivo sul lato lavorante: . Questi punti rappresentano posizioni specifiche all'interno di un sistema articolare che stiamo studiando. L'obiettivo è calcolare l'angolo tra il segmento che unisce i punti e e il segmento che unisce i punti e . Questo metodo è utile per determinare la relazione angolare tra due movimenti distinti nello spazio per cui come precedentemente si descrive il calcolo dei vettori ![]() Il vettore tra il punto e il punto : , Il vettore tra il punto 1Lm e il punto H₃: . Prodotto scalare: Il prodotto scalare tra i vettori e è dato dalla formula: , e sostituendo i valori calcolati: . Calcolo delle norme: Le norme (lunghezze) dei due vettori sono calcolate con la formula della lunghezza del vettore: e e della norma
Il vettore tra il punto e il punto : , Il vettore tra il punto 1Lm e il punto H₃: . Prodotto scalare: Il prodotto scalare tra i vettori e è dato dalla formula: , e sostituendo i valori calcolati: . Calcolo delle norme: Le norme (lunghezze) dei due vettori sono calcolate con la formula della lunghezza del vettore: e e della norma ![]() Le norme (lunghezze) dei due vettori sono calcolate con la formula della lunghezza del vettore: per giungere alla definizione del coseno dell'angolo tra i due vettori
Le norme (lunghezze) dei due vettori sono calcolate con la formula della lunghezza del vettore: per giungere alla definizione del coseno dell'angolo tra i due vettori
da cui si ottiene il
Infine, l'angolo \theta è calcolato tramite la funzione arcoseno:
Conclusione della cinematica incisale
L'analisi articolare dell'incisivo sul lato lavorante rivela dettagli significativi sulla dinamica e l'interazione tra i punti di riferimento durante il movimento mandibolare laterale. Utilizzando una combinazione di trigonometria vettoriale e prodotto scalare, è stato possibile quantificare con precisione sia la distanza lineare che l'angolo tra i segmenti che collegano i punti selezionati dell'incisivo, offrendo una visione approfondita del comportamento biomeccanico di quest'area.
In termini di spostamento lineare, l'incisivo lavorante mostra variazioni di distanza che riflettono la direzione e l'entità del movimento laterale e retrattivo e precisamenti di mm. Questi spostamenti, riportati nella tabella come valori in pixel e in millimetri, evidenziano una traiettoria complessa che è influenzata da fattori anatomici e dalle connessioni condilari, che guidano l'orientamento e l'ampiezza del movimento incisale durante la masticazione.
Dal punto di vista angolare, l'angolo tra i segmenti definiti risulta di circa. Questo valore rappresenta un'importante indicazione del grado di deviazione del movimento incisale rispetto all'asse laterale di riferimento. Un angolo di questa entità suggerisce un'ampia mobilità laterale dell'incisivo, tipica del movimento mandibolare laterotrusivo. Tale inclinazione riflette non solo la funzione masticatoria, ma anche la necessità di adattamento dei muscoli e dei tessuti circostanti per mantenere stabilità e precisione durante la funzione.
In conclusione, l'approccio matematico utilizzato per analizzare i movimenti dell'incisivo sul lato lavorante offre un quadro dettagliato delle dinamiche masticatorie. Questa analisi non solo contribuisce alla comprensione della biomeccanica mandibolare, ma fornisce anche una base di riferimento per applicazioni cliniche, come la diagnosi di disturbi temporomandibolari e la pianificazione di trattamenti riabilitativi. La conoscenza precisa degli angoli e delle distanze coinvolti in questo tipo di movimento può infatti supportare una valutazione accurata delle condizioni articolari e muscolari, migliorando l'efficacia degli interventi terapeutici.